基于概念生成中三个层面追问的问题串设计

龙艳文

(南京市教学研究室 210001)

1 问题的提出

一次调研中，笔者听了“直线的斜率”一课，下面是概念生成环节中教师设计的问题串：

问题1在日常生活中，我们经常会遇到楼梯，它的倾斜程度如何刻画的？

问题2你如何刻画直线的倾斜程度？

问题3在平面直角坐标系中，已知两点P(x1，y1)，Q(x2，y2)，如何刻画直线倾斜程度？

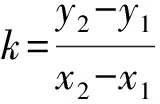
从上述设计可以看出，设置问题串引领课堂教学已成为教学的共识．如果基于概念生成中三个层面进行如下追问：(1)必要性，即要不要的问题．为什么要引入倾斜程度？为什么想到楼梯坡度？为什么要引入坐标系？(2)合理性，即好不好的问题．用线段成比例刻画直线倾斜程度好吗？用纵坐标与横坐标之差的比刻画直线倾斜程度好吗？(3)严谨性，即对不对的问题．用任意两点就能刻画倾斜程度吗？用两点坐标刻画直线倾斜程度全面吗？等等，我们可以发现本节课问题串虽然建构了对直线斜率认识的清晰流程，关注了对每个问题的解决，但很难解释上述三个层面的追问．因为每一个问题都是教师直接抛出，几个问题之间衔接显得生硬，只是让学生循着教师提出的问题逐步去解决问题，它忽略了学生发现问题、提出问题的过程，忽略了对概念生成性的理解，忽略了对数学问题研究基本过程的认识．

2 设计的改进

数学的发现是通过观察与活动发现问题、提出问题，进行检验推理、寻找反例、逻辑论证等过程解决问题或完善问题，所以概念教学不能只满足于告诉学生“是什么”或“什么是”，还应让学生了解概念的背景和引入它的理由，知道它在建立、发展理论或解决问题中的作用[1]．然而，教材只呈现了概念“是什么”或“什么是”的粗线条结构和最终的结论，所以教师需要重新对教材内容进行解构，以对数学问题的研究过程为脉络自然地展开概念的生成过程．

那么，如何按数学问题研究过程为脉络来展开呢？教师可以从概念生成过程中必要性、合理性、严谨性这三个层面的追问对上述案例的问题串进行一些改进．

环节一概念引入

引言数学倡导理性，生活也倡导理性，我们需要决定购买新的物品时，总是在有意或无意间追问：(1)我需要吗(必要性)？(2)它有什么用(合理性)？(3)它对什么无用(严谨性)？同样，对于数学中一个新的概念、新的定理、新的公式、新的方法等，我们也需要从必要性、合理性、严谨性这三个层面来追问．

前面我们从宏观的角度介绍了本章主要通过建立平面直角坐标系以代数的方法研究曲线和方程．那么，我们熟悉哪些曲线？从研究最简情况入手的策略，我们首先来研究什么曲线？

【学生活动预设】学生提出熟悉的曲线有直线、圆、椭圆、抛物线等，而其中最简形式为直线．

问题1在平面直角坐标系中，如何刻画一条直线？

【学生活动预设】通过学生交流讨论，提出一个点和倾斜程度、一个点和角度、一个点和方向、两个点等．

问题2既然同一条直线可以用不同的方式确定，从数学研究过程来看我们需要研究什么问题？

【学生活动预设】从数学是研究事物之间关系和规律的角度，引导学生提出研究确定直线的不同方式之间存在什么联系，尝试建立起它们之间定性和定量的关系．

【三个层面达成分析】通过引言切入本节课研究的整体方向．通过问题1对如何刻画直线进行开放式讨论，突破学生对原有直线的经验认识，为问题2的提出做好铺垫．通过问题2提出了一个比较大的研究话题，讨论研究的方向，提出了对直线研究的整体架构，从而解释了引入新概念的必要性．

环节二类比坡度

问题1前面我们提出了确定直线可以用倾斜程度，那么，在已有的经验中你在哪里见过倾斜程度？

【学生活动预设】引导学生从确定直线的不同方式中选择倾斜程度，联想先前的经验，特别是生活经验，提出山坡、楼梯等的坡度问题，从而体验到倾斜程度与生活的直接关系，体会到数学源于生活．教师可以展示一些相关的图片或视频来增强学生对坡度的认识体验．

问题2既然大家都提到了坡度，那现在有如下图的两个山坡，图1中AB和A′B′哪一个陡？图2中AB和A′B′哪一个段陡？

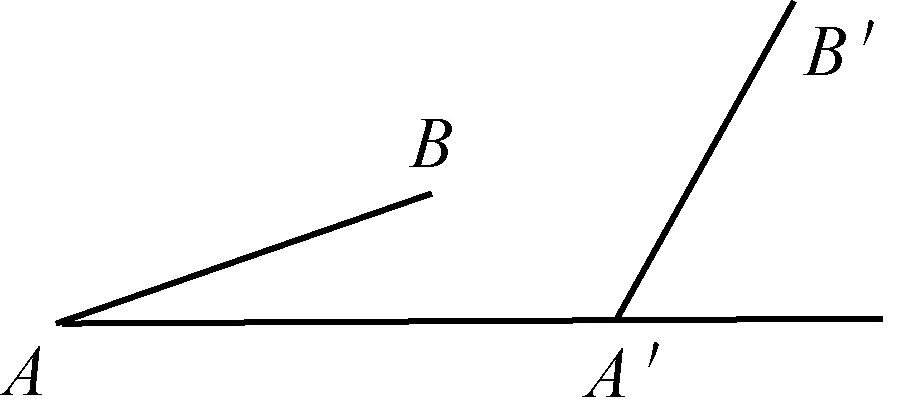
图1

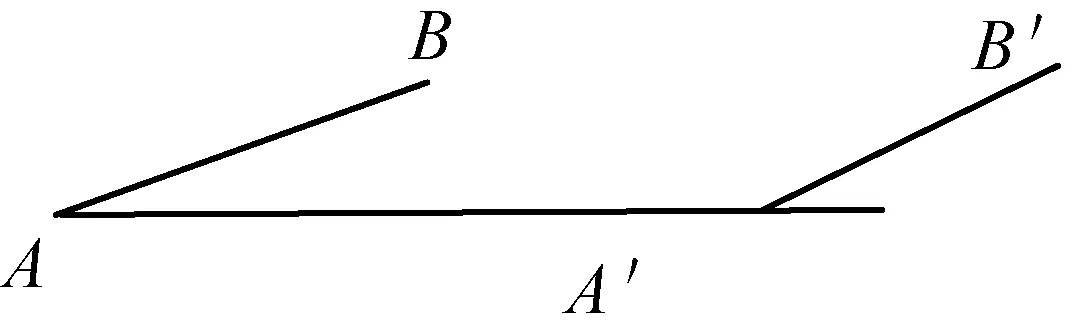
图2

【学生活动预设】对于图1学生可以直观地判断，而对于图2难以直观判断，从而产生认知冲突，引导学生从形显直观但难入微的困境，转而尝试用数的方法来进行定量判断，如通过长度比值判断或角度的判断等．

问题3类似地，前面提到的楼梯坡度如何刻画？

【学生活动预设】通过对问题2的分析，如下图，类似地得到如下定义：

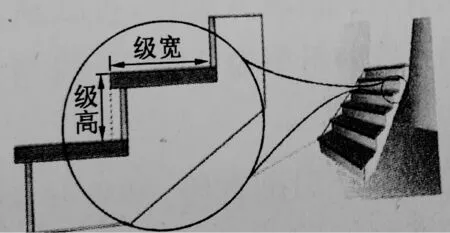
楼梯的坡度

问题4对于新概念的定义，我们需要考虑其合理性，即它有什么作用或规律？

【学生活动预设】引导学生体验新定义在解决陡峭程度时的作用，比如测量楼梯坡度时不需要测量整个楼梯的高度和宽度，只需选取一级台阶，即一个直角三角形．引导学生发现一些规律，如坡度值越大，楼梯越陡．再如楼梯台阶的级宽不变，那么每一级台阶的高度越大，坡度就越大，楼梯就陡．

问题5对于概念的定义，你能从严谨性角度提出什么疑问吗？

【学生活动预设】引导学生发现能构成的直角三角形有无数个，需要通过三角形相似论证它们的比值是否相同．

【三个层面达成分析】通过问题1对倾斜程度的经验联想，从而解释了引入山坡和楼梯坡度的必要性．通过问题2的认知冲突解释对坡度进行定量分析的必要性．通过问题3、4解释坡度定义的合理性．通过问题5解释定义的严谨性．

环节三生成概念

问题1类比楼梯的坡度，在平面直角坐标系中如何定义直线的倾斜度？

再从代数研究的角度通过坐标表示得到如下定义：

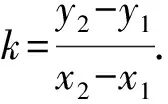
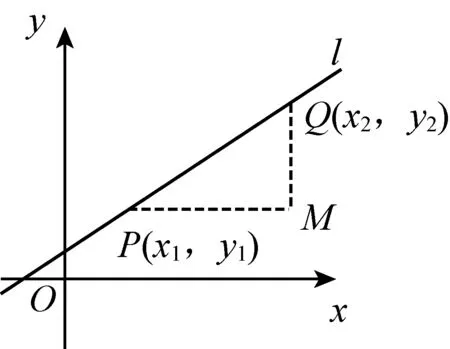
问题2我们对直线的倾斜程度有了一个新的名称和新的定量形式，它有什么合理性？

【学生活动预设】引导学生体验由斜率定义只要找到直线上不同两点的坐标，就能求出直线的斜率．

问题3比较上述两种定义形式，你能从严谨性角度提出什么疑问吗？

【学生活动预设】引导学生回到定义，分析第一种定义形式因线段长度表示而无法区分斜率为负的情形，第二种定义形式却能很好解决这个问题，但第二种定义形式因为x1≠x2，所以不能表示垂直于x轴的直线，而两个定义都需要论证P，Q的任意性．

问题4我们如何完善斜率定义？

【学生活动预设】引导学生在原有定义增加x1≠x2，补充特殊情形：如果x1=x2，则直线垂直于x轴，此时直线AB的斜率不存在．

【三个层面达成分析】通过问题1体验到引入坐标系和用坐标表示斜率的必要性．通过对问题2解释了定义的合理性，通过问题3、4解释了定义的严谨性．

附：对于教学设计教材版本选择的说明

苏教版教材对倾斜角和斜率的编排结构与人教版有比较大的差别．苏教版分为两个课时，第一课时直线的斜率，第二课时为直线的倾斜角，而人教版为一个课时．苏教版第一课时“以直线的倾斜程度如何刻画”为问题导引，类比楼梯或路面的倾斜程度用坡度刻画，即以水平线为参照系，再通过建立平面直角坐标系得出斜率定义，体现了从生活经验逐步过渡到坐标化处理，充分让学生经历引入坐标系的必要性和合理性，让学生体验解析几何用代数方法处理几何问题这一核心思想．第二课时再引入倾斜角定义，再建立斜率和倾斜角之间量化关系，再次体验解析几何的核心思想．而人教版以“平面直角坐标系内的一条直线l，它的位置有哪些条件确定”为问题导引，即直接以坐标系为参照系，先引入倾斜角定义，再类比坡度，引入斜率定义，再建立斜率和倾斜角之间量化关系．两个版本各有侧重、各有优点．考虑授课教师是基于苏教版教材的思路上课，本文是基于对本节授课的改进，从而本文的问题设计遵循了苏教版教材思路，而且仅提供了第一课时直线的斜率的问题设计．

3 三个层面的思考

数学概念来源于两方面：一是对客观世界中的数量关系和空间形式的直接抽象，二是在已有数学理论上逻辑建构[1]．基于对现实对象关系或数学逻辑结构的抽象产生认知冲突或需求，它是一种研究过程所遇到的困境，是概念生成的必要性，即要不要的问题．对必要性的分析是学生发现问题、提出问题的过程，是学生用数学的眼光观察世界的过程．为了能解决存在的冲突和需求，引入了新的概念，需要进行检验或论证，是概念生成的合理性，即好不好的问题．对合理性的分析是学生解决问题的过程，是学生用数学的思维分析世界的过程．对新概念的定义进行检验和论证的过程中，需要通过举反例、推敲表述等，考虑概念生成的严谨性，即对不对的问题．对严谨性分析是学生完善问题的过程，用数学的语言表达世界的过程．而且，对新的数学概念三个层面分析不仅是数学问题研究的过程，更是一种思维的理性精神，是一种敢于质疑、善于思考、严谨求实、一丝不苟的科学精神，从而促进学生数学核心素养的发展．

教师对教学中问题串的设计，不但要关注知识的逻辑结构，更应关注研究问题的一般方法，关注概念生成过程中学生的思维方式．所以，教师需要对概念的内容进行教学解构，将知识的逻辑结构和学生的思维方式结合起来，以研究问题的一般方法为暗线，从而将研究问题方法内化为学生的认知结构．对于新概念的教学，教师以概念生成的三个层面为脉络进行教学设计，根据学生已有的认知基础和经验，以必要性为起点，寻找新的知识 “孕育点”或“生长点”，引入新的概念形式，通过对其合理性与严谨性的逐步分析，理解概念的内涵与外延，形成概念的准确表述，并将其纳入到学生已有的概念系统．

另外，问题串的设计关键是通过问题让学生学会提出问题，分析问题，解决问题，学会思维、学会运用，学会反思[2]．所以，教师对问题串的设计考虑课堂教学中问题生成的主体是学生，而不是教师，问题的设计要如波利亚所说，让你的学生提出问题，要不就像他们自己提问的那样由你去提出这些问题[3]．那么，如何引导学生能从问题中生成问题呢？教师可以根据概念生成的三个层面为脉络，以学生自我提问的方式或教师象学生提问的方式进行追问，从已知问题中发现新的问题，挖掘新的问题，构建问题与问题之间的自然衔接，从而实现以知识为载体发展学生的思维能力和数学核心素养．