一个三角形不等式的证明与类比

贺 斌 孟凡海 闵 华

(湖北省谷城县第三中学 441700)

在△ABC中，设∠A、∠B、∠C的对边分别为a、b、c，则有如下不等式成立：

(1)

笔者查阅资料，未见有人给出(1)式的证明．为此本文将给出不等式(1)的证明，并通过类比，给出了两个与之类似的不等式．

我们先给出不等式(1)的证明．

证明因为在△ABC中有

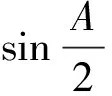
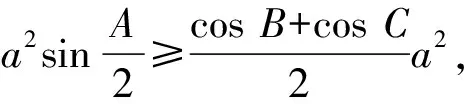
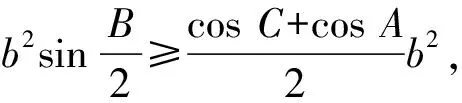
故欲证(1)式，只需证

(cosB+cosC)a2+(cosC+cosA)b2+(cosA+cosB)c2≥a2+b2+c2．

(2)

由余弦定理知， (2)式⟺

(b2+c2)cosA+(c2+a2)cosB+(a2+b2)cosC

≥2bccosA+2cacosB+2abcosC

⟺

(b-c)2cosA+(c-a)2cosB+(a-b)2cosC≥0．

(3)

不妨设A≤B≤C，则∠A、∠B均为锐角，

cosA、cosB>0，且c-a≥b-a≥0．

从而 (c-a)2≥(b-a)2，

进而有 (c-a)2cosB≥(b-a)2cosB，

所以

(c-a)2cosB+(a-b)2cosC

≥(a-b)2(cosB+cosC)．

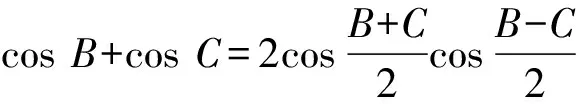
所以(c-a)2cosB+(a-b)2cosC≥0，

又(b-c)2cosA≥0，

将以上两式相加知：(3)式成立，从而原不等式(1)成立．证毕．

类比不等式(1)，笔者发现，在△ABC中，如下的两个不等式也是成立的：

(5)

(4)式的证明

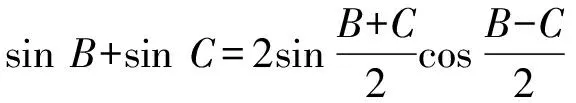
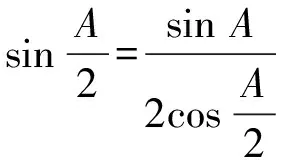
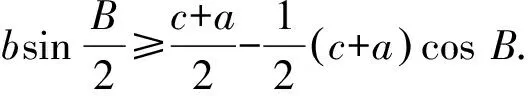
将以上三式相加，并注意到a=bcosC+ccosB等三式，得

+(ccosA+acosC)+(acosB+bcosA)]

(5)式的证明

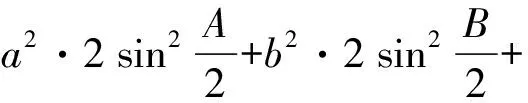
⟺a2·(1-cosA)+b2·(1-cosB)+

⟺a2cosA+b2cosB+c2cosC

(6)

不妨设A≤B≤C，则

a2≤b2≤c2，cosA≥cosB≥cosC，

于是，根据切比雪夫不等式知

a2cosA+b2cosB+c2cosC

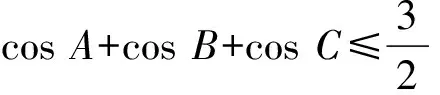
沿着本文的思路，读者还可以提出一些类似的不等式，这里还有较大的探索空间．