数学学习就是一场深度对话

张格波

(南京市江宁高级中学 211100)

人们通过对话实现信息的传递、思想的交流和情感的表达．就这个角度而言，我们可以认为数学学习就是老师与学生、学生与学生之间的深度对话．通过深度对话，可以让学生经历表达一步步完善的过程；通过深度对话，可以让学生的思考层层深入，逐步抓住本质；通过深度对话，可以让数学课堂充分发挥出自己的教育价值．本文试借助于苏教版《函数周期性》的教学过程，阐述笔者的理解．

1 数学学习就是深度对话

事实上，由于各个学生的生活经历、体验都不相同，关于周期现象的前概念也不相同，因此即使面对相同的情景，他们说出的理解也不相同．这样恰好为多角度地理解周期现象提供了可能，教师通过不断的追问：还可以怎么看？使得学生不断转换思路，在不断的对话中，学生对周期现象的理解走向了深入，逐步完成对函数周期性概念的建构．以下是对话的片段．

1.1 还可以怎么看？——引领对话走向深入

教学环节1：展现周期现象与周期函数图像

1)周期现象很多：时针、天干、地支、属相、寒来暑往、潮起潮落等．山海关城门对联刻画的也是这种现象：海水朝 朝朝朝 朝朝朝落；浮云长 长长长 长长长消．

2)函数作为对实际生活的一种数学表达，也具有周期性，比如正余弦函数．

3)问题：这些现象有何共同的特点？

学生1：很多出现了重复．

师：什么意思？

学生1：有些现象一段一段地出现了重复．

师：什么是一段一段地出现重复？

学生1：……

师：还可以怎么看？

学生2：周而复始．

师：好，一句话高度概括，简洁明了，抓住了关键．

师追问：周而复始中的关键词是什么？

学生2：周，就是间隔；复，就是重复，再次出现．

师追问：很好，能否说得更加具体呢？比如周是一个间隔，它具有何种特征？

学生3：它是固定的，不变的．

师：什么意思？相对谁不变？

学生3：相对于整个变化过程是不变的，也就是说它是一个常数，常量．

师追问：很好，周是一个常量，常数．还能认识到其它特征吧？

学生4：它不能等于零，等于零没有意义．

师追问：大家的认识越来越深入，还可以认识到什么？

学生4：周的整数倍还是周，比如海水涨潮，一天是周期，一月也是周期，整数倍都是周期．

师：他的结论正确吗？大家都是这样认识的？

学生(众)：是的．

师：看另一关键词：复，还可以进一步地理解吧？比如，是什么在重复？是怎样重复的？

学生5：是某种现象，全部重复出现．

师追问：进一步解释清楚，对函数来说：1)你这里“全部”什么意思？2)是什么在重复？

学生5：所有函数值都重复．就是说，所有函数值每间隔一个周期后，就重复一次．

师：好，我们将刚才的结论汇总一下，填写在这张表中再来体会一下．

周期现象关于周的认识关于复的认识周是什么?谁在重复?怎样重复?潮起潮落寒来暑往正弦函数余弦函数

评析在此教学环节中，教师通过展现生活中的周期现象与熟悉的周期函数图像，激活学生原有的生活经验与前概念；通过在师生之间、生生之间的对话让学生形成了整体的、模糊的、粗略的认识——周而复始．在这个过程中间，我们发现口头语言其实是学生数学思维外显的载体．让学生“对话”，就是让学生通过语言表达他们的思维．

1.2 这可以作为一般性的判断依据吗？——在质疑中，抓住本质

学生6：虽然我们画不出它的图像，但我们还是可以判断出它是周期函数．

师：为什么呢？

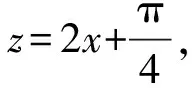
师：这能作为一般性的判断依据吗？外函数是周期函数的时候，原函数就是周期函数？

学生：……

师：前面的经验是什么？这个函数有“周而复始”的现象吗？

师：你怎么就看出来函数值相等的？

学生7：计算后发现的．

师：我想问的是，你怎么想到去看函数值是否相等的？

师追问其他人：他的判断方法能作为一般性的判断依据吗？

学生8：不行，他列举的只是一些特例，不能说明所有都有这种特征．

学生7：我找不到反例．

师：找不到反例，说明这个函数可能真的是周期函数，但如何进行一般性的说明呢？

学生7：……

学生9：我想起来了，这个函数是周期函数，周期就是2π．

师：怎么说？

日语形容词“旨い”可表示多个义项，如①表示美味，香甜，好吃，饮食物的味道好；②好，巧，善于，顺利。对自己有利，自己所期望的状态；③用于惯用句“旨い汁を吸う”中表示揩油，占便宜，不劳而获，自己不付出辛苦而得到利益等。④用于惯用句“旨い話し”中表示有利可图的事情，条件合适和非常方便的事。对于日语形容词的多个义项现象，学者们进行过较充分的研究。例如，武藤(2001)从认知语言学视角出发，分析了形容词“甘い”的语义拓展方式，指出其各个义项并非彼此孤立存在而是相互关联，拓展义基本上都是通过隐喻或转喻等认知机制对原型义进行的拓展。本文将以“旨い”的多个义项为基础，通过考察其后续名词的词性来进行分析。

师：没有反例？每个人都这样认为的？

学生10：没有反例，上述等式中的自变量可以是任意的，即它是一个恒等式．

学生11：周期还可以改为π．因为

师：其他人的认识呢？有不同意见吗？

学生：……

师：受此启发，回头看，能否从恒等式的角度来说明y=sinx，(x∈R)是周期函数呢？

学生12：能，因为sin(x+2π)=sinx，所以y=sinx，(x∈R)是周期函数，周期是2π．

师(追问)：那函数y=cosx，(x≠π)是周期函数吗？

学生12：是，因为cos(x+2π)=cosx，所以y=cosx是周期函数，周期也是2π．

师(追问)：其他人的认识呢？有不同意见吗？

学生13：不对，它不是周期函数．因为cos(-π)=cosπ，但x≠π，也就是说有一个点无法被重复，因此它不应该是周期函数．

师(追问)：那将函数y=cosx，(x≠π)的定义域怎样修改，又变成了周期函数呢？

学生(众)：去掉限制，定义域改为R．

师(追问)：还可以怎样呢？

学生：……

学生14：把那一串都去掉，改为y=cosx，(x≠kπ，k∈Z)．

师(追问)：为什么呢？

学生14：这样就没有反例，也就是说cos(x+2π)=cosx，对定义域任意自变量恒成立．

师(总结)：所以说，周而复始，是指所有函数值都要重复，就是等式要恒成立．

评析在本教学环节中，教师通过让学生判断一个暂时画不出图像的函数是否是周期函数，逼着学生从抽象的解析式这个角度来研究周期性．这样，学生就必须要想办法实现用符号化的代数恒等式来刻画“周而复始”．在学生寻找办法的过程中，教师反复用“这能作为一般性的依据吗？”、“其他人的认识呢？有不同意见吗？”、“为什么？”引导发言者表述自己的思维过程，同时也引导其他学生去理解、去质疑别人的表述，从而使得所有学生深入理解．因此，“对话”不仅仅意味着让学生讲出不同的想法给他人听，更重要的是要在理解他人的想法中做出比较和判断．实际上学习就是在一个群体中互动的体验过程，就是一个具有“社会协商”性质的主动建构过程[1]．

1.3 我们都知道了什么？——在概括中建立概念，形成理性思维意识

师：从上述过程来看，关于周期函数，我们都知道了什么？

学生11：就是周而复始，其中“周”是一个常数，不能为零，它的整数倍也是周期；“复”就是函数值出现重复，就是自变量增加周期后，函数值不变．

师：还有补充的吗？

学生12：要全部重复，即自变量要能取遍定义域内的每一个值．

师：很好，那么一般地，函数y=f(x)要满足什么条件才能是周期函数呢？

学生13：满足f(x+T)=f(x)恒成立，其中T是一个非零常数即可．

师：很好，在寻找周期函数的本质特征的过程中，你有什么收获？

学生14：透过现象抓本质．

师：具体一点呢？

学生14：就是要看出“周而复始”就是等式f(x+T)=f(x)恒成立．

师：还有呢？

学生14：判断时，必须要有一个一般性的依据，要以理说话．

评析经过前两个阶段的对话、讨论，学生对于函数周期性已经积累了一定的认识，初步完成了对本质的抽象．因此，本教学环节主要就是让学生将周期函数的各个方面性质联合起来考察，也就是进行概括．教师通过“我们都知道了什么？”、“还有补充吗?”来启发学生进行概括．事实上，在教师的启发下，学生不仅完成了对知识的概括，还谈到了对整个思维过程的体验——要以理说话，这就是理性思维意识．

2 深度对话就是学生与数学本质的对话

从上述过程我们可以看出，通过对话，学生的表达一步步走向完善；通过对话，学生的思考层层深入，逐步抓住本质．因此，数学课堂上的对话就不仅仅表现为学生与教师、学生与学生之间的语言交流，更是学生与数学本质的一种对话[1]．换句话说，就是因为对话走向了数学的本质，我们才称之为深度对话．

我们知道，周期现象的数学本质就是等式f(x+T)=f(x)恒成立．要形成这种认识，学生必须要经历两次抽象．第一次是形成对周期函数的初步抽象——周而复始．第二次抽象，就是建立形式化、符号化的数学表征——等式恒成立．在第二阶段，学生需要突破三个思维上的关键点，第一个就是为什么要进一步形式化．作为教师，我们知道只有达到这种符号化、形式化的程度，才可以进行推理论证．但是怎样才能让学生也体会到呢？第二个关键点是要将生活中的“重复出现”改用数学中的等式来表达．第三个关键点就是学生要认识到等式是恒成立的，定义域中的每一个自变量都要满足这个等量关系．

这两次抽象，是一个认识上的飞跃，如果让学生独立地、完全自主地去完成，是困难的．虽然“重复”本身蕴涵相等的含义，但如果教师不点拨，不让学生给予关注，学生往往意识不到．于是，对话与交流就为思维的展开提供了基础．在第一阶段抽象中，教师借助于周期现象与周期函数图像，让学生谈自己的认识，通过“还可以怎么说？”，让学生多角度阐述自己的观点，在多角度的对话中学生形成了“周而复始”的初步印象．通过对“周而复始”关键词的辨析，更进一步能清楚了细节：周是什么；谁重复，怎样重复？虽然都是用自然语言表达的，但为第二次抽象做好了准备．

在第二阶段，教师通过让学生判断一个暂时画不出图像的函数是否是周期函数，使他们意识到自己能力上的缺陷，从而引发了认知上的不平衡，感受到有必要用抽象的解析式来表达出函数的“周而复始”．这时，学生也不是一下子就成功的，而是在不断的尝试与对话中，相互启发、质疑，才使得学生逐步意识到为了用解析式来刻画“重复”，必须要用数学中的等式来表达“重复”．学生先是从外函数的角度来试探，由于无法深入，教师及时纠正了方向：能否从周而复始的已知经验来说明？然后，学生想到了特殊值检验函数值是否相等，这样，数学本质出现了．后来再通过反例，教师的追问，这样大部分学生才认识到这个等式还必须是恒成立的，从而让学生不断地接近于符号化，形式化．显然，没有前面的对话，这个学生不可能直接想到它．这一场对话就是要让学生多角度理解自然界中的“周而复始”与数学恒等式之间的关系，从而实现用“代数恒等式”来形式化地刻画“周而复始”．这场对话就是学生与数学本质的对话，在此过程中学生也体验到了数学抽象的意义与价值．

3 深度对话需要教师的引导

学习就是学生与数学本质逐步对话的过程，在此过程中，学生要将模糊的思维理顺后再清晰表达出来，要让自己的认识不断条理化、清晰化，逐步走向概念的本质．那如何组织好数学课堂上的对话，以促进学生思维走向深入，逐步接近于数学的本质呢？结合本人的教学实践，我觉得可以努力做好以下几点．

3.1 做好深度对话的主持人

第一、通过激励，形成平等、积极的对话氛围．1)我们要理解学习的心理机制，给予学生表达的机会．就数学概念而言，学生要面对大量的实例，通过观察，比较，分析和综合，抽象与概括等思维过程，才能将感性的认识上升为理性，这个过程就包括讨论，交流，互动等组织活动．没有对话，就没有思想的相互启发；没有社会协商，就没有深度理解．2)学会等待，做好平等中的首席．我们知道问题是有挑战性的，解决它是需要时间的，给足时间，才能使学生的发言是经过充分准备的，主动性才能得到保护．3)学会评价，呵护学生的自尊．教师对学生的对话要及时点评，好在什么地方，错在什么地方，要用简洁、明了的语言给与评价．同时要学会救场，为回答不出的学生提供适度的支持与帮助．

第三、引导归纳、总结．本节课中，教师先是通过一张表来让学生进行知识上的总结，形成初步的认识；后来，又通过提出问题“我们都知道了什么？”让学生再次进行概括，从而建立了概念．当然，我们不能忘记让学生对认识过程进行表达，只有这样，才能让学生逐步形成理性认识方式．

3.2 关注深度对话的教育价值

从教学过程可知，师生通过对话，拉长了“抽象”过程，完成了 “社会协商”，实现了意义建构，对话的作用是显著的．首先在对话的过程中学生获得了启发：对话就是思想的交换，学生在理解了别人的交流后，就多了一个理解数学的角度．其次，在交流与讨论中理会越辩越明：学生通过质疑、对比、推敲是否能推广到一般，加深了对数学概念的理解；同时通过对事物多方面性质的概括，抓住了概念的本质．

但我们不仅要关注对话的内容，更要关注深度对话的教育价值．比如，学生通过对整个思维、对话过程的概括、内省，提高了理性思维的意识．再者，在对话过程中学生也逐步学会表达：为了说明自己的想法，为了更好地表达自己，必须要深思，力争抓住关键，在表达过程中，还要注意到语言的逻辑性，缜密性，简洁性．所有这些，都体现了数学的教育价值．因此，在引导进行总结、概括时，我们不能仅仅满足于让学生进行知识上的总结与对话，还要对整个思维过程进行交流，表达自己对思维过程的感受、体验，以形成稳定的认识方式，建立理性思维意识．

总之，我们认为数学学习就是一场深度对话，就是学生与数学本质的对话，在对话的过程中学生建立了对数学的深刻理解，发展了理性思维意识，实现了数学的教育价值．