高三三角函数复习策略实验研究

夏春南

(江苏武进区鸣凰中学 213164)

1 问题的提出

《普通高中数学新课程标准(实验)》指出：高中数学课程应注重提高学生的数学思维能力，这是数学教育的基本目标之一.人们在学习数学和运用数学解决问题时，不断地经历直观感知、观察发现、归纳类比、空间想像、抽象概括、符号表示、运算求解、数据处理、演绎证明、反思与建构等思维过程[1].而三角函数是基本初等函数之一，在中学数学中处于核心地位，对培养学生数学思维能力至关重要[2].

三角函数和代数、几何、平面向量等有着密切的联系，是高中数学的重要内容，也是高考考查的重点内容之一，高考每年至少命制一大题和一小题.从近几年各省高考卷可以看出，三角函数的试题重基础，起点低，考查全面，涉及三角函数的性质，三角函数的化简与求值，解三角形及三角函数的综合运用.

笔者所在学校生源质量一般，学生的数学基础和学习能力较薄弱，而三角函数的解答题一般位于解答题第一题，部分学生由于基础知识薄弱，基本数学思想和方法不熟练，往往不能在较短时间内顺利作答，这对学生的整体数学成绩及心理状态至关重要.因此，如何在高三复习中夯实学生三角函数的基础知识，提高高三复习效率值得研究.

本文旨在通过对高三三角函数的复习进行前测与后测，对实验数据进行研究和分析，以期形成高三三角函数的复习策略，从而为高三三角函数的复习提供理论依据，对高三复习阶段课堂教学的效果起到积极的推动作用.

2 研究方法

2.1 研究被试

研究采用实验研究方法，以本校高三386名学生为研究对象，全部编号参加.

2.2 研究工具

(1)前测卷的编制

前测卷一方面需针对高考题型进行整体设计，既要覆盖所有的知识内容，又要考虑所涉及的思想方法，以及测试问卷的难易程度，试题的先后位置，另一方面，考虑前测工作是在学生新课结束后，一轮复习前使用，故难度不能太大.从近几年的高考情况看，三角函数一直是考查的重点，并且是大题形式，前测试题共5题，每题20分，满分100分.

题1：(2015年江苏省高考15题)

在△ABC中，已知AB=2,AC=3,A=60°,(1)求BC的长；(2)求sin2C的值.

此题属于解三角形类型，主要考查余弦定理及二倍角公式.

题2：(2014年江苏省高考15题)

此题属于三角求值类型，主要考查同角三角函数关系式、两角和差的正余弦公式、二倍角公式，须特别注意余弦的符号，钝角的三角函数值.

此题属于三角函数图像类型，已知函数图像求函数解析式，第一问中代入求φ，已知三角函数值求角，要注意角的范围，第二问考查二倍角公式和两角和差的正弦公式.

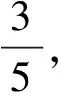
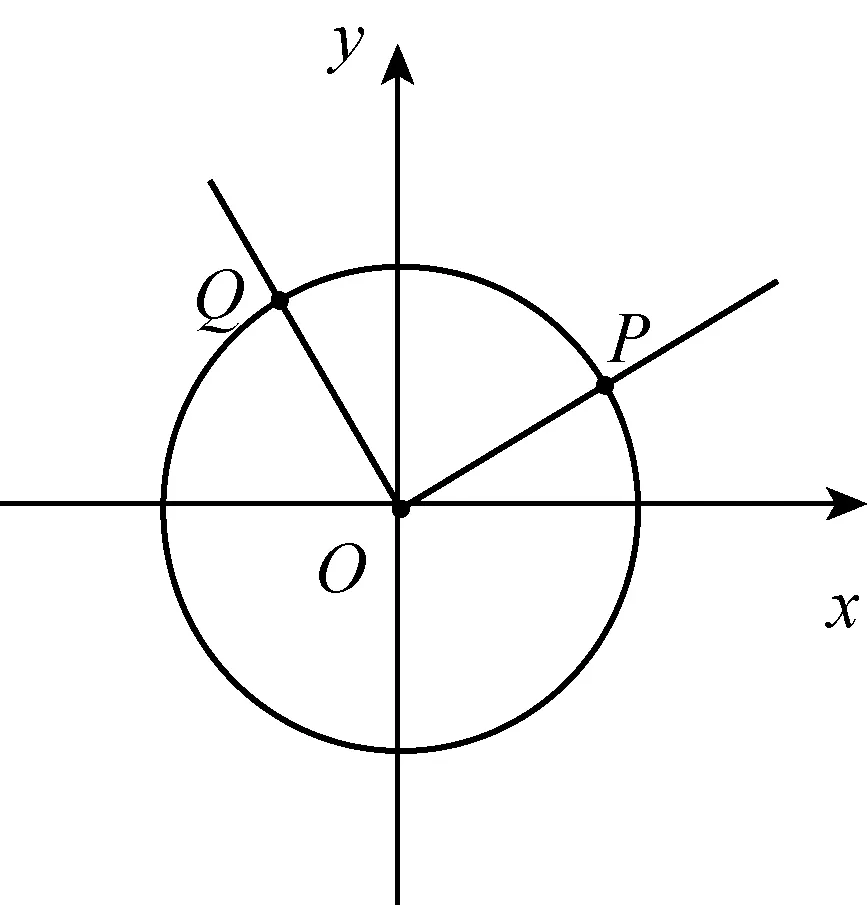
(1)设∠COA=θ,求sin2θ的值；

(2)若△AOB为正三角形，求点B的坐标.

此题以单位圆为载体，主要考查三角函数的定义，二倍角的正弦和两角和的正余弦公式.

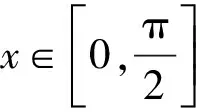
此题第一问考查了两向量平行的充要条件及两角差的正切公式，第二问属于三角函数图像与性质类型，涉及二倍角的倒用、辐角公式，是一道与向量结合的综合题.此题要求学生对三角函数的定义有清晰的认识.

(2)后测卷的编制

就前测中发现的问题，有针对性地进行教学，查漏补缺，专项训练.后测卷是对三角函数复习效果的检测，后测卷主要考查学生综合应用三角函数的能力，因此难度较前测卷略高.

题1：(苏锡常镇四市2015届高三教学情况调研二第15题)

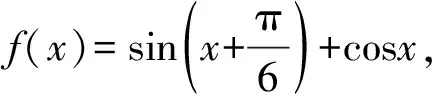
(1)求函数f(x)的最大值，并写出当f(x)取最大值时x的取值集合；

题2：(南通市2015届高三第一学期期末试卷第15题)

在△ABC中，角A,B,C所对的边分别为a,b,c，已知b·cosC+c·cosB=2a·cosA,

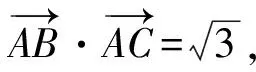
题3：(扬州市2015届高三第一学期期末考试第15题)

(1)求函数f(x)的解析式；

题4：(2015年南京市、盐城市高三第一次模拟考试第15题)

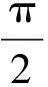
(1)求函数f(α)的值域；

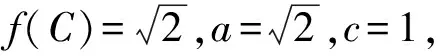
题5：(盐城市2015届高三第三次模拟试卷)

(1)求函数f(x)取最大值时x的取值范围;

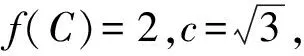
2.3 研究程序

运用多种研究方法主要有调查问卷研究法、实验研究法、比较研究法、行动研究法及经验总结法，对被试对象实施高三三角函数复习的前期测试和后效测试.

2.4 统计方法

对研究的测试结果利用SPSS19统计软件进行数据输入整理以及分析处理.

3 研究结果与分析

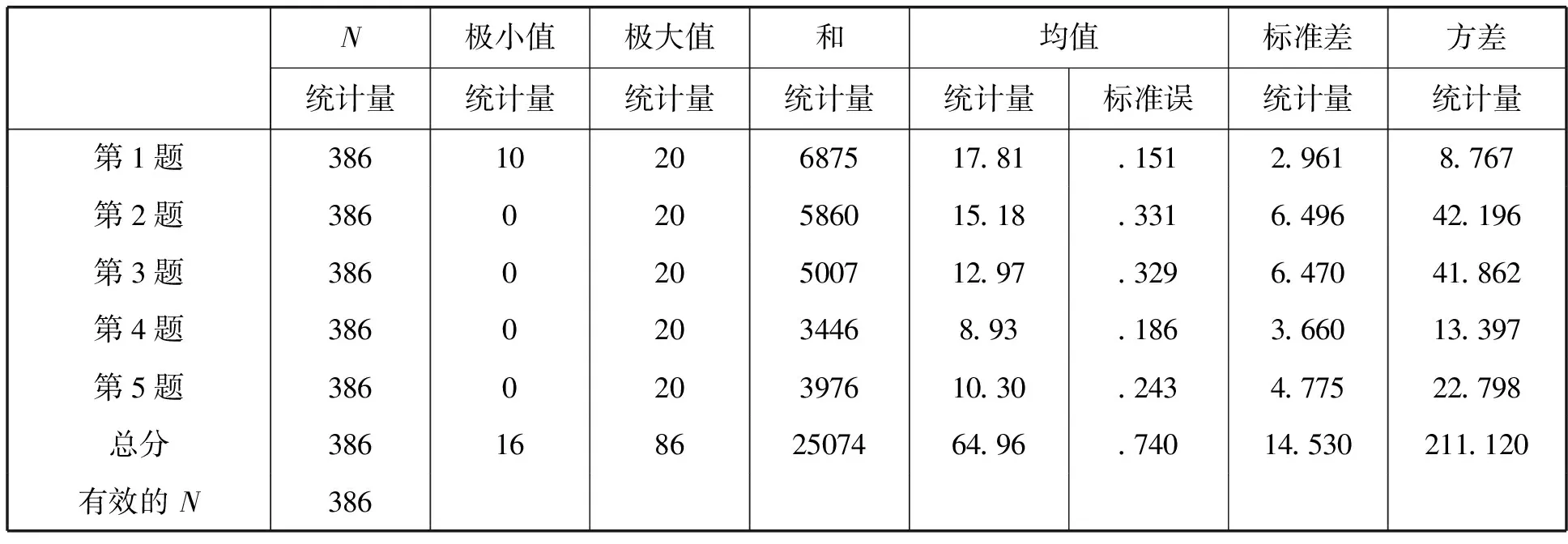
表一 前测卷测试结果

从表一可以看出，学生对三角函数的掌握处于中等水平，第4题中，对三角函数的定义理解不到位，点B的坐标不会用两角和差来表示，第5题主要的失分在于二倍角的倒用，辅角公式化简不准确，其中第1题的标准差最小，差异性最小.

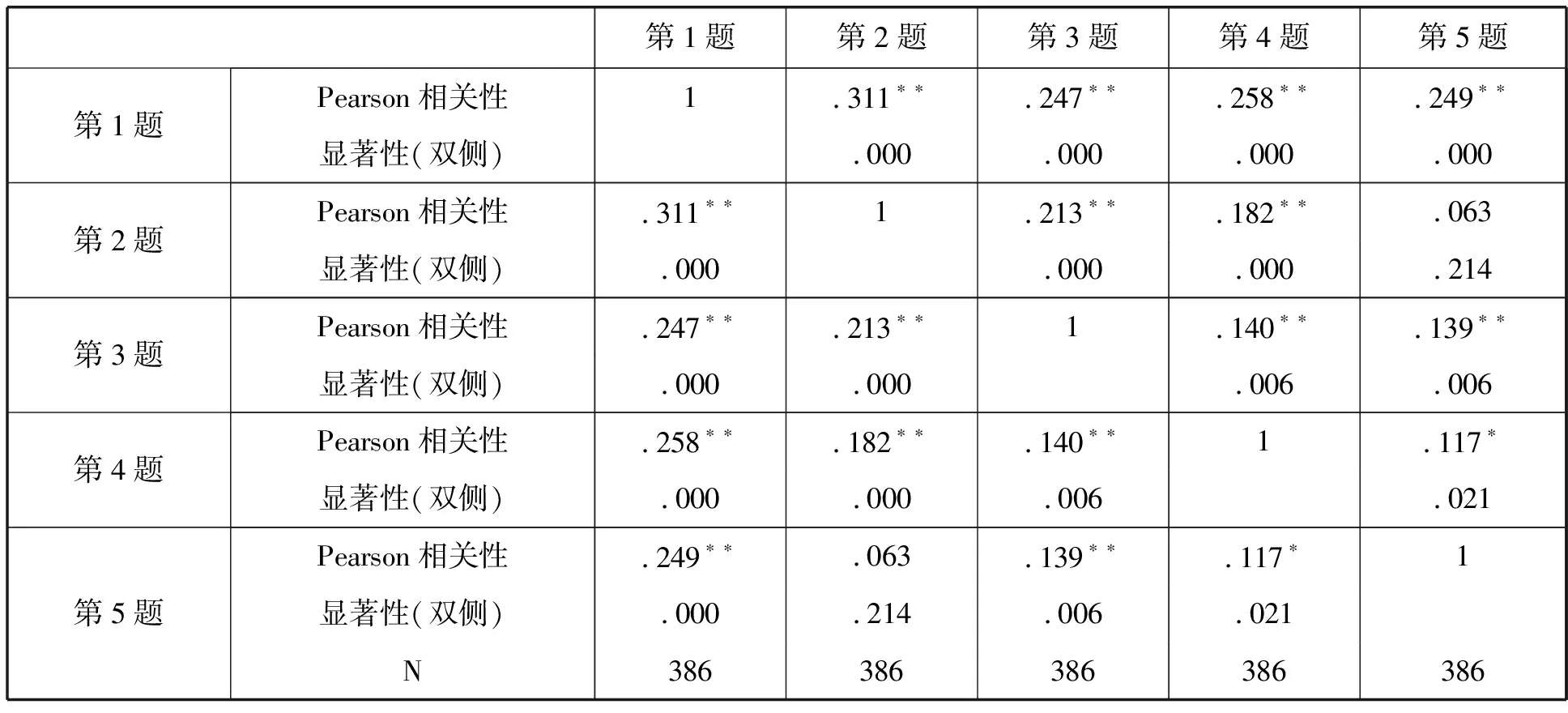
表二 前测卷成绩相关系数

**.在 .01 水平(双侧)上显著相关，

*.在 0.05 水平(双侧)上显著相关.

由表二可以看出，第1题与第2题、第3题、第4题、第5题的解答，第2题与第3题、第4题的解答，第3题与第4、第5题的解答呈偏强相关，反映了三角函数内部知识间是紧密联系的，三角函数化简与求值能力直接影响了其它问题的求解，第4题与第5题的解答弱正相关，第2题与第5题的解答不呈相关关系，反映了学生在三角函数与其它知识相结合上的短板，这些综合问题的求解需要灵活运用所学知识.

表三 后测卷测试结果

后测卷整体难度略高于前测卷，从表三可以看出，学生对三角函数的掌握程度明显高于前测卷.通过对学生问题进行有针对性的复习，学生的整体解题水平有了较大提高，如第1题的解答均值达16.05分，第2题的解答均值高达18.61分，其中特别是对三角函数定义的理解掌握程度有了明显的改观，该题满分的学生也较前测中多.

4 结论

从实验数据可以看出，在一轮复习前，通过对三角函数进行前测，可以发现学生这部分的掌握情况及存在问题，便于在后面的复习中有针对性制定复习计划，提高复习效率；在实验后，再对学生进行实验后测，便于了解学生前阶段的学习成果，为高三三角函数的复习提供有价值的建议，从而形成高三三角函数的复习策略.

(1)重视概念、公式的生成过程，做到基础知识夯实

要重视对三角函数定义理解、重要公式的推导过程，特殊角的三角函数值的记忆等等.

(1)求tan(α+β)的值，(2)求α+2β的值.

又如在2011年陕西文理卷大题直接考查了：叙述并证明余弦定理，对课本定理的直接考查起到了良好的导向作用，这就要求我们复习中必须重视课本，回归课本，理解课本上的定义的生成，重视重要公式定理的推导，特别是考试说明中要求掌握的内容，一定要理解和掌握，该记忆的内容要熟记，如特殊钝角的三角函数值，诱导公式等，对常规的解题方法要烂熟于心，要做到夯实基础知识.

(2)重视三角大题的训练，做到重点题型强化

三角函数一直是高考中考查的重点，而且必有一大题出现.而大题的题型相对固定，主要有三角函数求值问题、解三角形问题、三角函数图像与性质及三角函数综合问题.三角函数求值问题.

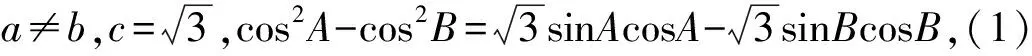
解三角形问题不再是正余弦定理直接的应用，有一定的难度，对三角式子的化简要求较高，特别是降幂公式，内角和定理，辐角公式等；三角函数图像与性质问题

这几类题型在全国各省市高考卷中频繁出现，因此需对这部分内容精讲精练，既要让学生熟练掌握解题思路，如解三角形遇到有边有角问题，常规思路利用正余弦定理统一化成边或角；如已知三角函数值求角问题，一要注意角的范围注意事项，二要选择合理的三角函数；对于一些典型的、容易出错的问题，学生要清楚知道哪些地方容易失分，如辐角公式后面的角度，两角余弦公式的符号等这样一些细节，对这样一些重点题型要求学生通过限时训练、周末练习、章节测试等不断强化，不断反复，最终达到重点题型熟练化.

(3)课堂教学以学生的问题为专题，做到难点问题解决

学生成绩的提高最有效途径就是解决学生的问题所在，只有习题没有问题是高三复习需要特别注意的.在三角函数重点题型的强化中，会不断反复出现一些问题，而这些问题会一直困扰着学生的学习，此时一堂非常有针对性的讲评课是非常有必要的.

通过实验研究发现，高中三角函数复习过程中，以三角函数基础知识点为顺序的教学和以学生问题为专题相结合的教学模式，是建立和夯实三角函数知识链的重要手段.

陶行知先生说过：“好的先生不是教书，不是教学生，乃是教学生学”.在课堂教学中，要突出学生的主体性：可采用“先练后讲，先思后讲，合作探究”的教学方法，对正确率高的题目可让学生总结解题规律，对正确率低而学生会的题目，可投影出错误的解答，让学生讨论指出错误，对学生不会的题目，学生思考片刻，让学生说说思路(或可在教师的点拨下)，最后让学生解答.

在课堂教学中，要重视解题规律的总结.题目解完不能就此束之高阁，要经常反思，既要对解题知识进行总结，更要把解题规律的总结作为解题总结的首要内容；在课堂教学中，还要重视解题的变式训练.变式训练是提高课堂教学效率的重要手段，每年高考中都会有很多题目来源于课本，或从课本习题中演变而来，解题后经常想想变式，“貌似而神不似” 、“貌不似而神似”等等，如能做到举一反三，融会贯通则必能提高解题能力.

(4)重视三角综合题的训练，做到思想方法提升

近几年高考中，三角函数与平面向量、导数、不等式(线性规划)、数列、解析几何的联系都比较密切，这些题目往往难度比较高.复习时可有意识选一些这样的综合题，有助于培养学生解决综合性问题的能力，有助于培养学生思维的灵活性和思维的深度.

此题考查函数的零点的判断，利用导数研究函数的单调性，体现了等价转化、数形结合的数学思想.

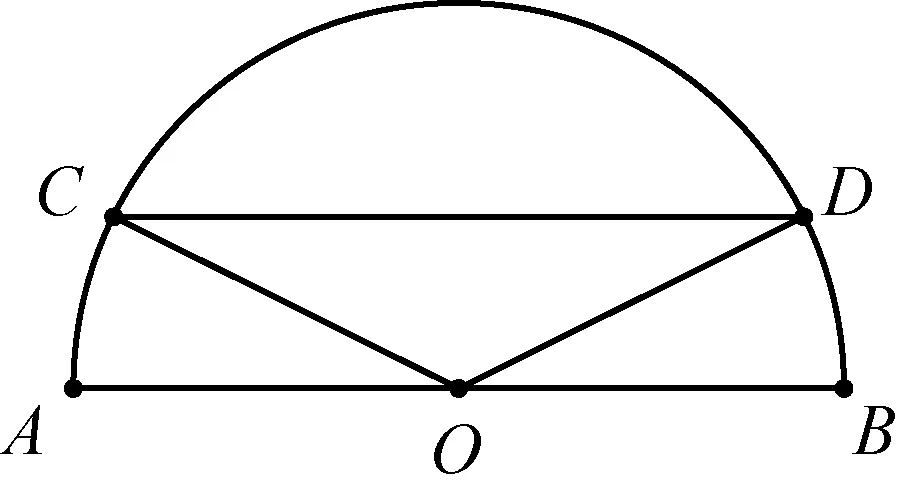
在三角综合题中特别还需注意的有三角函数的应用题：如图是一个半圆湖面景点的平面示意图，已知AB为直径，且AB=2km，O为圆心，C为圆周上靠近A的一点，D为圆周上靠近B的一点，且CD∥AB,现在准备从点A经过C到D建造一条观光路线，其中A到C是圆弧AC,C到D是线段CD,设∠AOC=xrad,观光路线长为ykm，(1)求y关于x的函数解析式，并指出该函数的定义域；(2)求观光路线总长的最大值.

可以转化为三角函数求最值的问题一般更为简单，而利用导数三角函数的最值是高考常考题型.

(5)重视错题集整理，做到错题有反思

专家研究发现，绝大多数高考状元都有使用错题本的习惯.错题本是夯实学习基础，提升学习成绩，提高考试信心的重要手段.每次试卷上的错题正是考试的价值所在，也是下次成绩提高的源泉所在.如何做好一本高质量的错题本，学生个体情况不同，所用方法也不尽相同，有的老师建议学生写出出错原因、考查知识点是个不错的方法.错题本整理关键在于坚持，坚持整理错题，日复一日，隔断时间反复订正，长此以往，必定会大有收益.错题本的另一好处在于通过错题本的整理，督促一些平常没有订正习惯的学生可逐步养成订正的习惯、反思的习惯.