典型花生种子脱壳特性试验及有限元仿真研究

侯俊铭，杨 勇，董 帅，何 涛，白晶波,李金澎

典型花生种子脱壳特性试验及有限元仿真研究

侯俊铭，杨 勇，董 帅，何 涛，白晶波,李金澎

（沈阳农业大学工程学院，沈阳 110866）

为研究花生种子机械脱壳变形和等效应力变化规律，改进脱壳装备设计，以辽宁地区主栽品种花育23和鲁花1号花生种子为研究对象，以破壳力和变形量为试验指标，加载速度、含水率、加载方式和品种为影响因素，对花生种子作单因素试验分析，建立花生壳和花生仁有限元模型，采用ANSYS软件对其静力学仿真。结果表明，加载速度、含水率、加载方式和品种对破壳力均影响显著（p＜0.05）；加载速度增加25%，破壳力和变形量下降7.54%及2.11%；含水率增加6.6%，破壳力和变形量上升19.7%及8.5%。花生壳不同加载方式有限元仿真最大变形量分别为2.34、3.23和3.86 mm，变形量与压缩载荷之间存在非线性关系，花生仁最大变形量约为花生壳的32%，试验结果与有限元仿真相近。研究为优化花生种子脱壳设备关键部件设计，降低脱壳破损提供参考。

花生；力学特性；有限元；压缩试验；ANSYS

花生是重要油料和经济作物[1]，花生种子脱壳质量影响其播种产量，研究花生种子脱壳力学特性对优化脱壳设备关键部件具有重要意义。脱壳是花生种子精加工必要工序，也是造成其损伤主要环节，脱壳特性是研究重点[2]。吕小莲等研究通过挤压破碎试验，分析品种、含水率和挤压位置对花生种子挤压性能影响[3]；王京等分析几何直径、百粒重及品种对其均齐性影响[4]。Dilmac等通过计算花生种子几何直径、体积、球度、休止角、孔隙率及表面积，分析花生壳体密度、颗粒密度、压缩指数及压缩指数与含水率关系，研究花生种子动态摩擦系数及不同结构表面含水率[5-8]，通过瞬态传热试验，分析花生种子比热容、导热系数和热扩散系数[9]。目前多集中于花生种子物理和力学特性研究，因花生种子几何非线性等特点，静压力学试验无法确定花生种子各部位力学参数变化过程。因此，静压力学试验和有限元法（FEM）结合方法应用广泛。史建新等利用静压力学试验和有限元仿真方法研究核桃、板栗以及冬小麦挤压力学特性参数对其受力和变形影响[10-12]；李震等利用ANSYS软件建立双锥度模具限元模型，对秸秆压缩特性作数值模拟发现，不同物料压缩特性规律相似[13]；王京等从试验和有限元仿真角度分析花生仁组织内部应力和应变，但未开展组织内部各点等势值变化及仿真结果与试验对比研究[14]。针对花生种子内部受力变形研究较少。

本研究针对花生种子受力特点，以ANSYS软件对花生壳和花生仁有限元仿真，计算花生种子变形量等势值数值解，对比分析压缩过程中受力及位移，为开发高效脱壳设备提供理论依据和参考。

1 材料与方法

1.1 材料

选用辽宁地区主栽的鲁花1号和花育23号花生种子开展静压力学试验，测定鲁花1号和花育23三轴尺寸，根据测量数据获得鲁花1号和花育23尺寸参数直方图（见图1）。鲁花1号三轴尺寸比花育23大15%左右，厚度略低于花育23。因此，花生种子在机械脱壳过程中，不同品种脱壳特性不同。

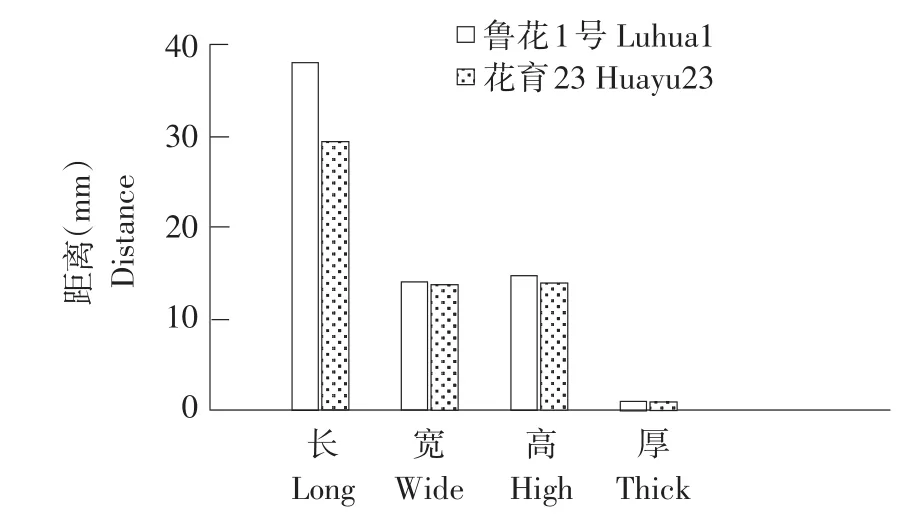
图1 花生几何参数尺寸Fig.1 Peanut geometric parameter size

1.2 试验装置

采用游标卡尺（精度0.02 mm）测量花生种子三轴尺寸；SFY型红外线水分测定仪（精度0.01，购自冠亚电子科技有限公司），快速测量花生种子含水率；LDS型微机电子万能试验机（购自美特斯工业系统有限公司），测量花生种子破壳力和变形量。LDS型微机电子万能试验机如图2所示。

图2 LDS型微机电子万能试验机Fig.2 LDS Microcomputer control electronic universal test machine

机架上压头装有压力传感器，操作面板控制上压头与花生种子间距离。调节上压头与花生种子距离不变，启动机器，以设定速度静态压缩，当花生种子压缩载荷下降至峰值40%时，停止压缩，压力传感器将压缩过程数据记录后处理，分析压缩位移与压缩载荷变化。

1.3 方法

采用控制变量法研究加载速度、含水率、加载方式和品种对花生种子破壳力、变形量影响，即固定其他因素，改变单一因素，分析该因素对破壳力和变形量影响。试验时，选取含水率15.52%鲁花1号花生种子，以10 mm·min-1加载速度试验，获得压缩载荷与压缩位移关系。

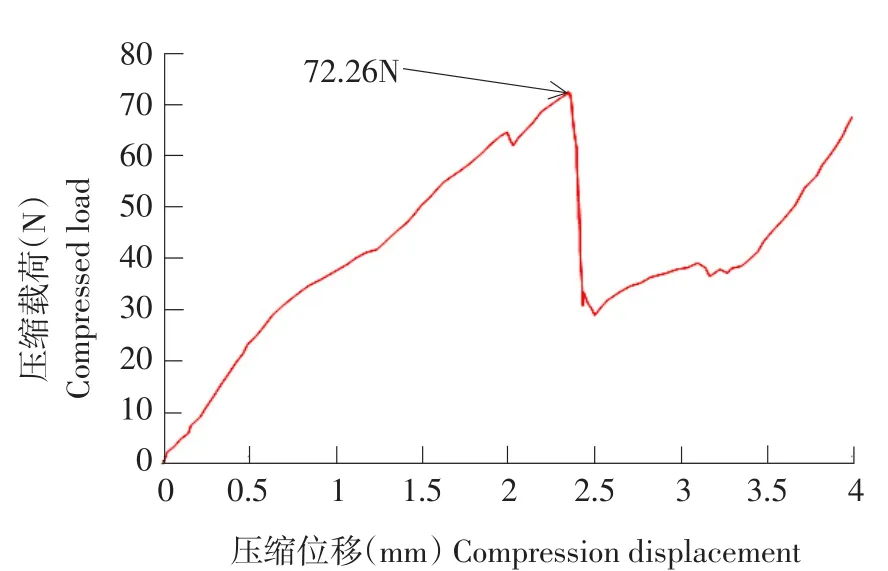
图3 鲁花1号花生压缩载荷与压缩位移变化曲线Fig.3 Curve of load and displacement of Luhua 1

由图3可知，随压缩位移增加，压缩载荷从0~70 N，压缩载荷先降至最低值再缓慢升高。说明花生种子受力破壳时，花生壳受力产生塑性变形，持续加载时，花生壳受力达应力极限，花生壳出现裂纹，直至破壳结束。花生种子受压后破损特征见图4。

图4 花生破损特征Fig.4 Peanut damage characteristics

1.4 数据分析与处理

1.4.1 加载速度对破壳力和变形量影响

为分析不同加载速度对破壳力和变形量影响，在其他因素不变情况下，选取含水率15.52%鲁花1号花生种子开展静态压缩试验，试验分为4组，每组重复4次，计算破壳力和变形量均值，获得不同加载速度下破壳力和变形量数据。

由表1可知，保持其他因素不变，变形量随加载速度增大而减小，加载速度增加25%时，破壳力和变形量分别下降7.54%和2.11%。

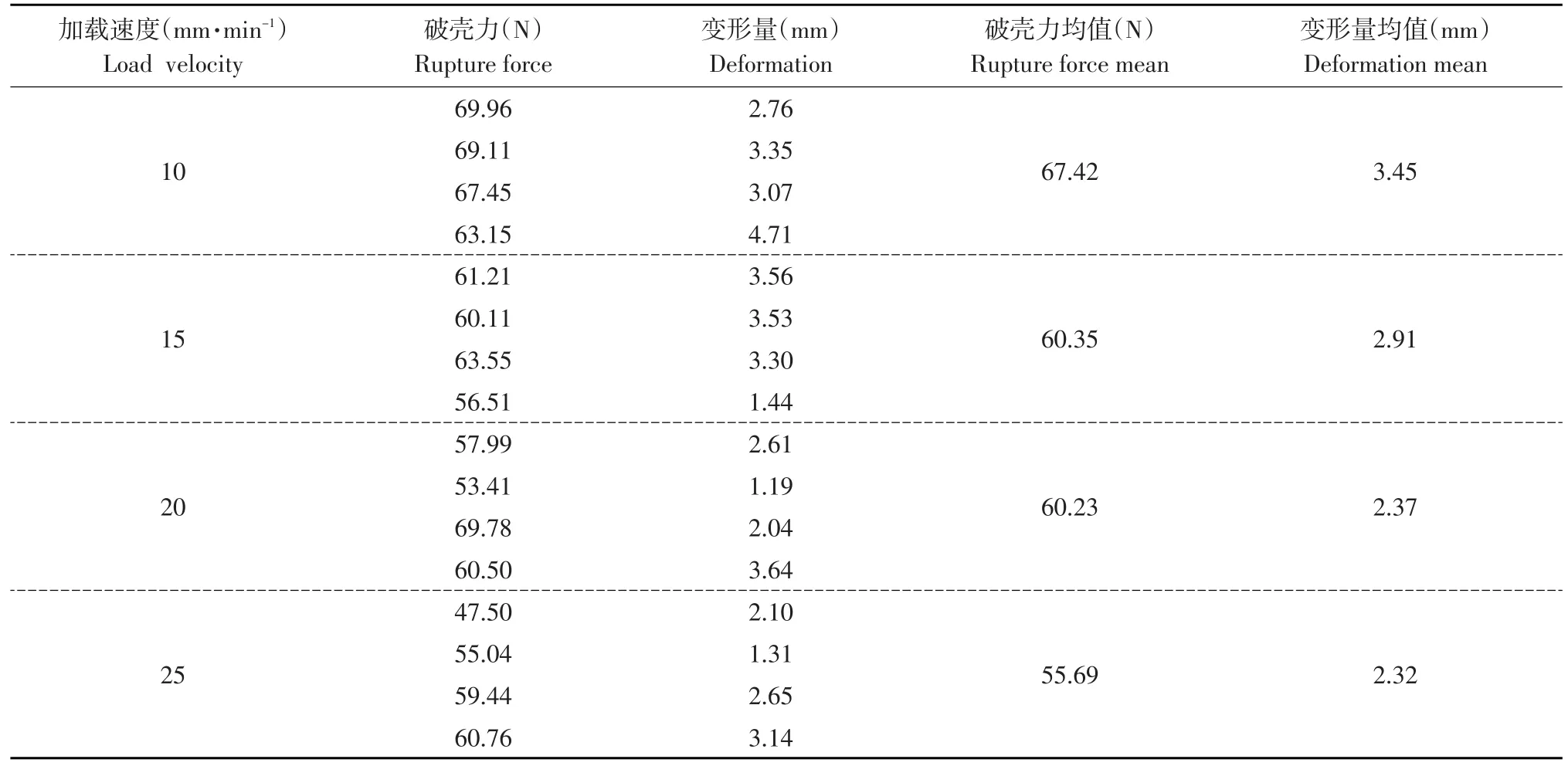
表1 不同加载速率破壳力与变形量Table 1 Rupture force and deformation at different loading velocity

由表2可知，在置信度为95%情况下，加载速度对破壳力影响中，检验水平p＜0.05，说明加载速度对破壳力影响显著；加载速度对变形量影响中，检验水平P＞0.05，说明加载速度对变形量无显著影响。为深入研究加载速度对破壳力和变形量影响，建立加载速度与破壳力和变形量一元线性回归模型，获得破壳力及变形量与加载速度一元线性回归方程分别如下：

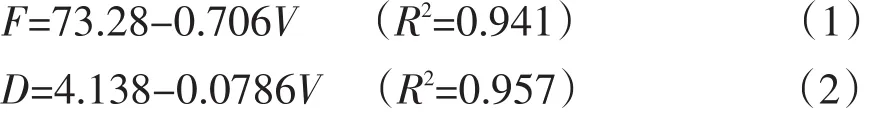
式中，F-破壳力（N）；V-加载速度（mm·min-1）；D-变形量（mm）。

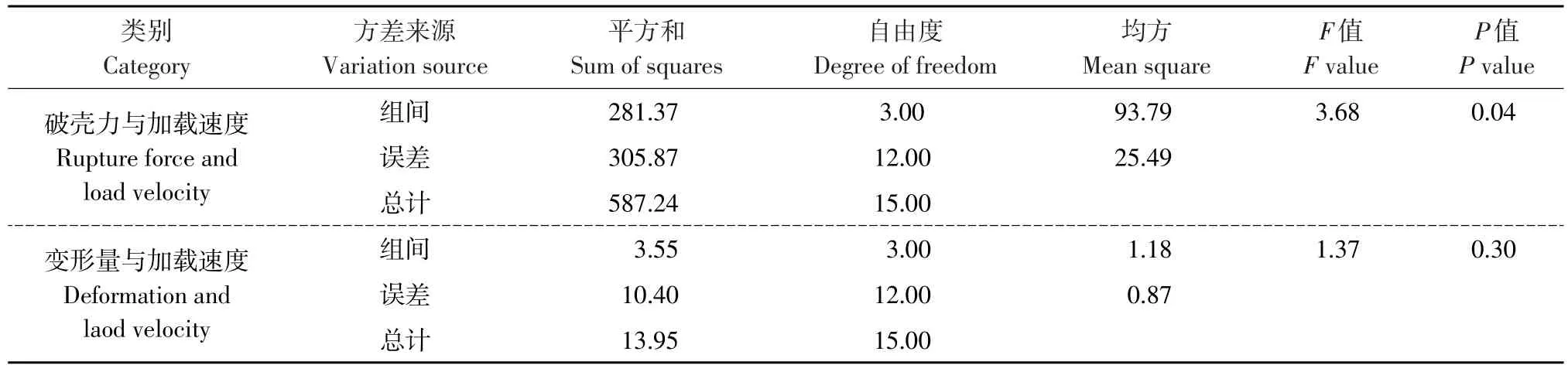
表2 破壳力（变形量）与加载速度方差分析Table 2 Variance analysis of rupture force(deformation)and loading velocity

由图5和图6可知，随加载速度提高，破壳力和变形量减少。主要因加载速度增大，单位时间内花生种子所受机械能增加，花生种子受力破壳趋势增大，所需破壳力和变形量降低。提高加载速度，有助于花生种子破壳。1.4.2 含水率对破壳力和变形量影响

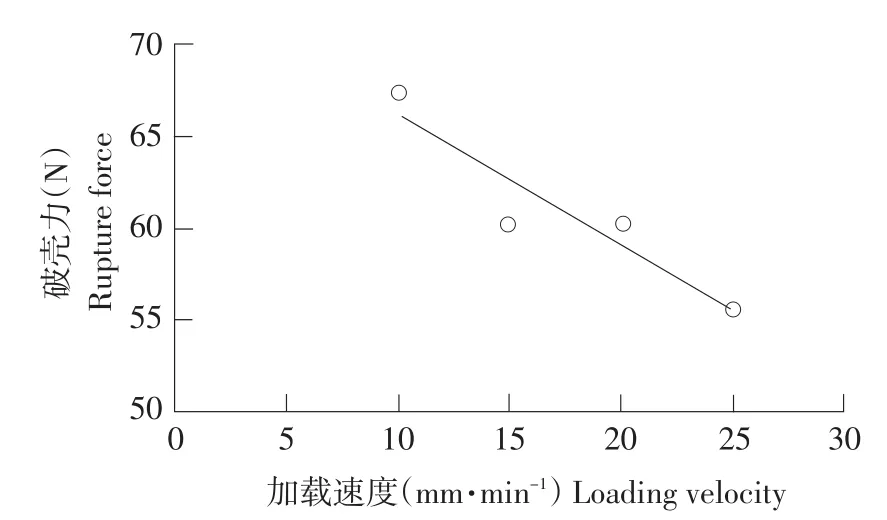
图5 加载速度与破壳力关系Fig.5 Relationship between loading velocity and rupture force

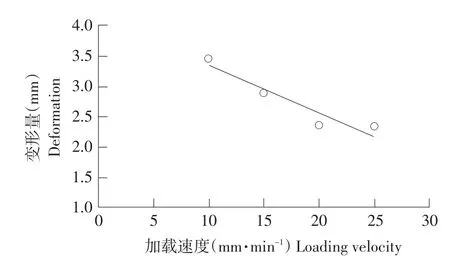
图6 加载速度与变形量关系Fig.6 Relationship between loading velocity and deformation

选取含水率分别为2.08%、8.97%和15.52%鲁花1号花生种子以20 mm·min-1速度开展静态压缩试验，试验分为3组，每组重复10次，计算破壳力和变形量均值，如表3所示。随含水率增加，花生种子破壳力和变形量不断增加，含水率增加6.6%，破壳力和变形量分别上升19.7%及8.5%。含水率对花生种子破壳力和变形量影响见表4。在置信度为95%情况下，二者方差分析结果中，检验水平p＜0.05，说明含水率对破壳力和变形量均影响显著。Iraj认为花生种子破壳力与含水率之间存在强烈多项式关系[15]。为深入研究含水率对破壳力和变形量影响，分别建立含水率与破壳力和变形量一元线性回归模型，获得破壳力及破壳变形量与含水率一元线性回归方程分别如下：

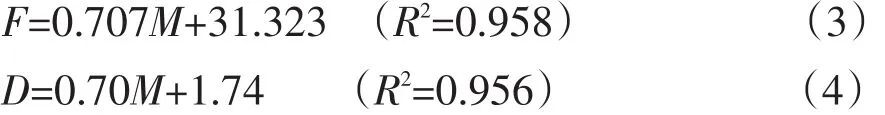
式中，F-破壳力（N）；M-含水率（%）；D-变形量（mm）。

由图7、8可知，随含水率增加，破壳力和变形量相应增加。花生种子在不同含水率下，力学特性不同，含水率越低，花生壳韧性越小，抵抗破裂能力越小。原因是花生壳主要由纤维素和粗纤维组成，仁壳间隙较小，仁易破碎，含水量越低，花生壳韧性降低，破壳前变形量减小。

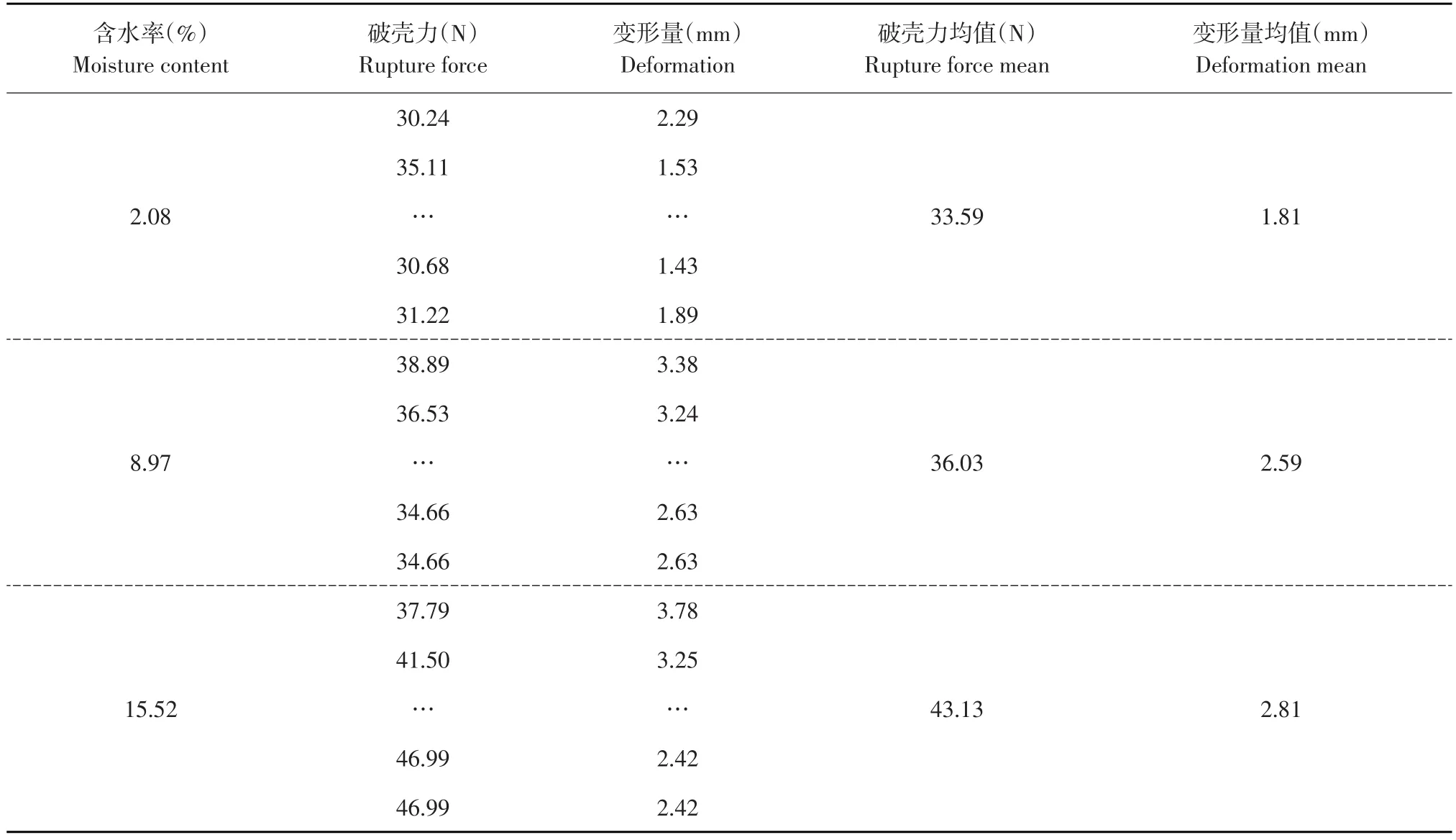
表3 不同含水率下破壳力和变形量Table 3 Under different moisture content of the rupture force and deformation

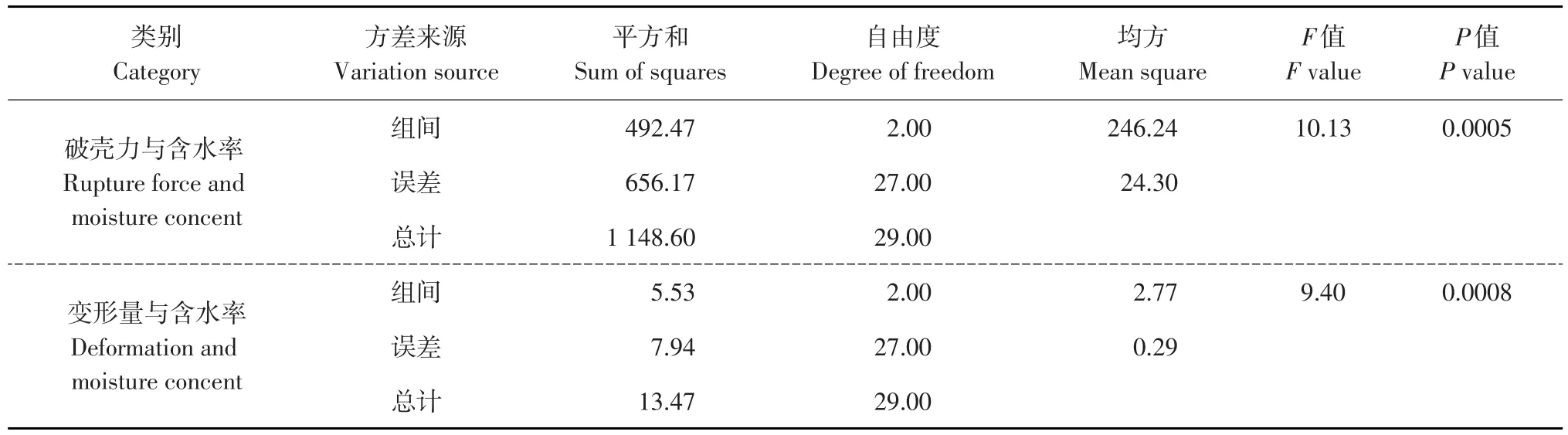
表4 破壳力（变形量）与含水率方差分析Table 4 Variance analysis of rupture force(deformation)and moisture content

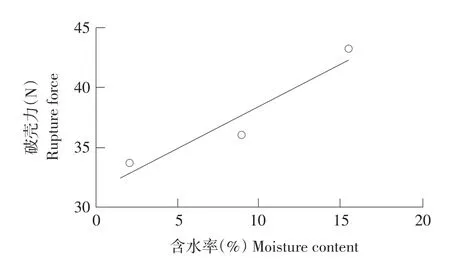
图7 含水率与破壳力关系Fig.7 Relationship between moisture content and rupture force

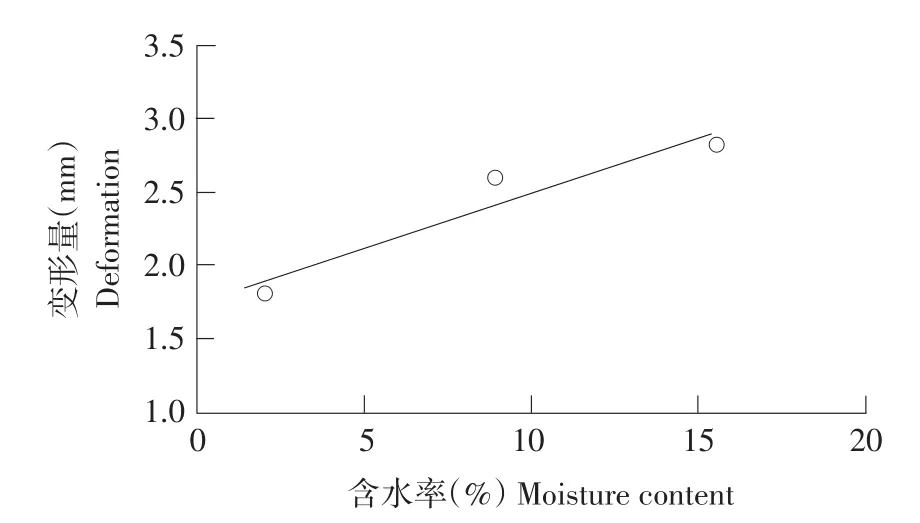
图8 含水率与变形量关系Fig.8 Relationship between moisture content and deformation

1.4.3 加载方式对破壳力和变形量影响

以含水率15.52%鲁花1号为对象，分别选取正放和侧放两种压缩方式，以10 mm·mim-1速度开展静态压缩试验，每种压缩方式5次重复试验，计算破壳力和变形量均值（见表5）。

为研究加载方式对花生种子破壳力和变形量影响对表5数据作单因素方差分析。获得不同加载方式下变形量与破壳力关系曲线。由图9可知，在相同变形量情况下，正放小于侧放加载所需破壳力。

由表6可知，在置信度为95%情况下，二者检验水平p＜0.05，说明正放加载和侧放加载对破壳力和变形量影响显著。由图9可知，随变形量增加，正放加载破壳力明显小于侧放。因此，正放较侧放加载更有利于花生种子破壳。

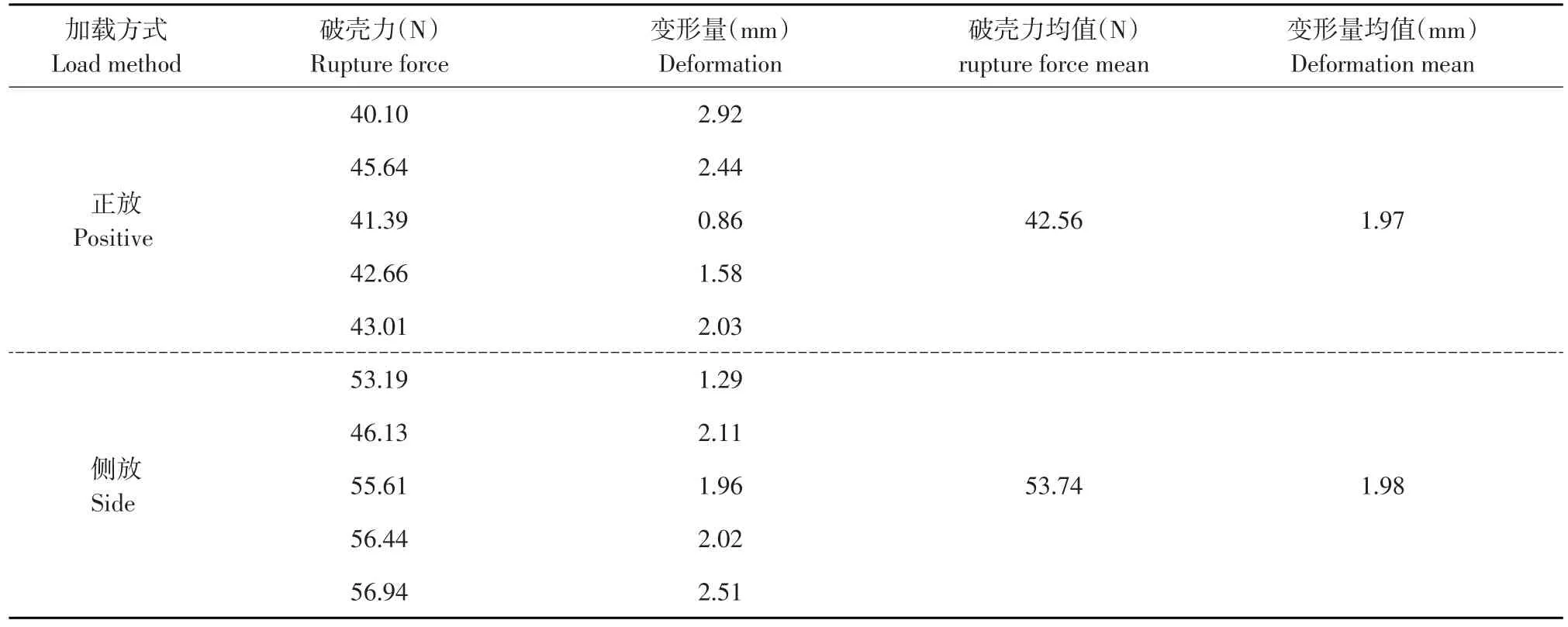
表5 加载方式对破壳力和变形量影响Table 5 Effect of loading method on rupture force and deformation

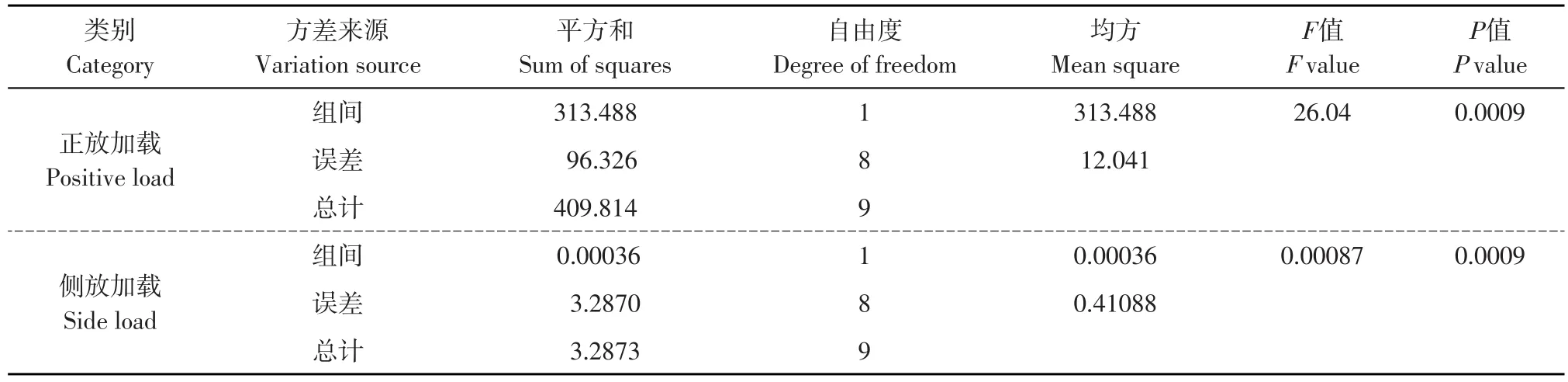
表6 加载方式对破壳力(变形量)方差分析Table 6 Variance analysis of loading method on the rupture force(deformation)

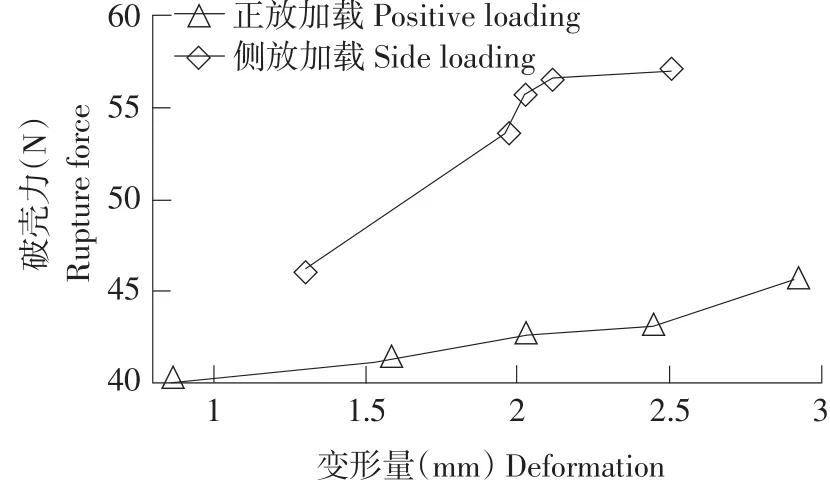
图9 加载方式对破壳力和变形量影响Fig.9 Effects of load method on rupture force and deformation

1.4.4 品种对破壳力和变形量影响

选取含水率为8.97%花育23和鲁花1号各10个，分为两组，以20 mm·min-1加载速度开展正放静态压缩试验，每组试验重复10次，计算破壳力和变形量均值，获得破壳力和变形量数据（见表7）。

由图10可知，花生种子载荷压缩时，不同品种破壳力和变形量不同，除个别点误差外，在相同变形量时，鲁花1号破壳力小于花育23。因鲁花1号三轴尺寸略大，与压头接触面积大，且花育23壳稍厚。因此，在相同试验条件下，鲁花1号花生更易破壳。

2 花生种子物理模型建立

2.1 花生种子几何模型

依据鲁花1号花生测量三轴尺寸，设计花生种子三维实体模型。花生仁长20 mm，宽14 mm，厚10 mm，花生种子几何模型及花生仁模型见图11。

2.2 花生种子破裂准则

花生壳主要由纤维素和半纤维素组成，纤维素和半纤维素在压力作用下至破坏前塑性变形较小，将其认定为脆性材料，失效形式通常是断裂。因此，当花生种子最大应力σ1达到极限应力σb时，花生壳破裂，即满足花生种子破裂准则为σ1=σb

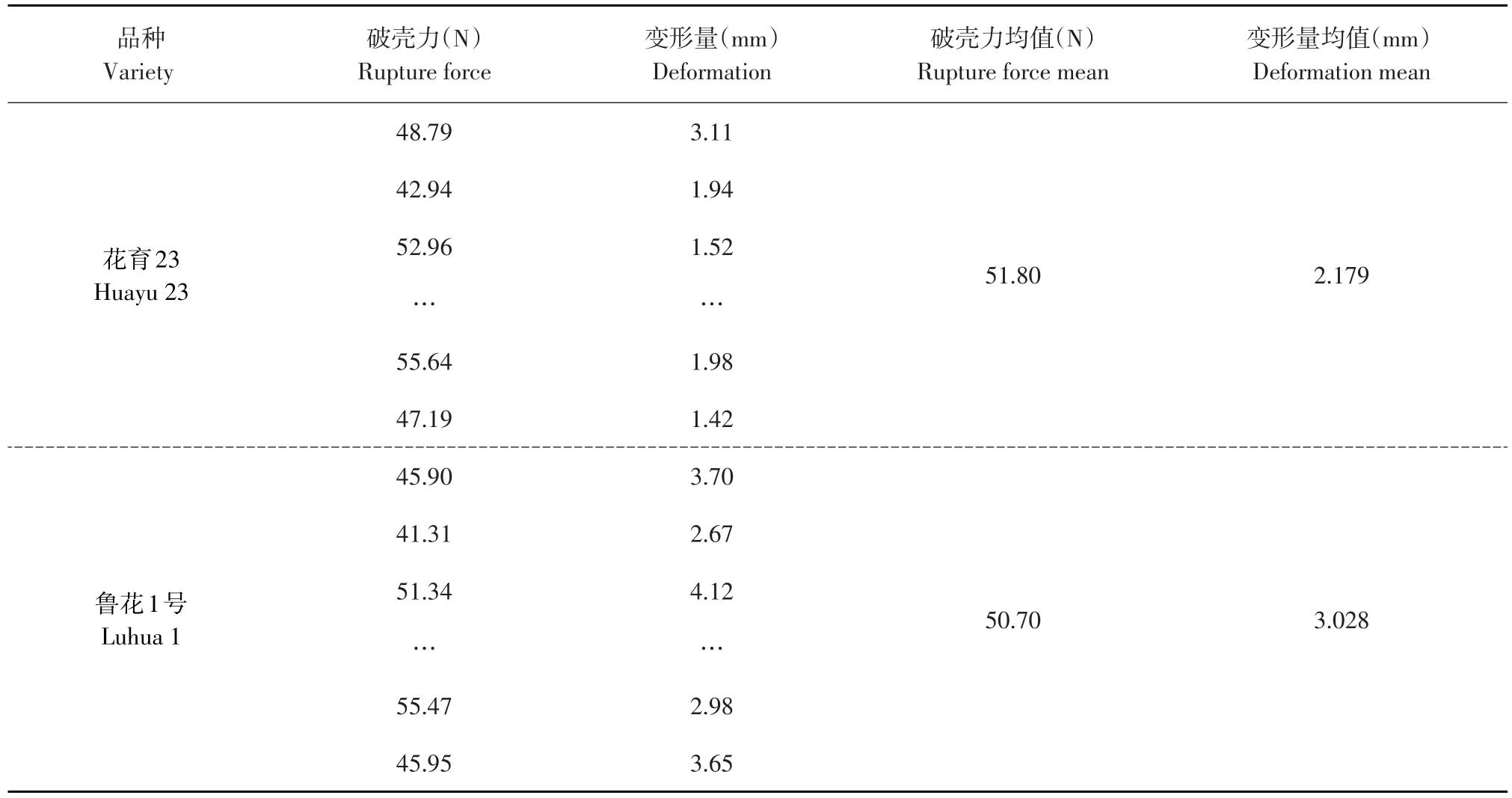
表7 品种对破壳力和变形量影响Table 7 Effects of varieties on rupture force and deformation

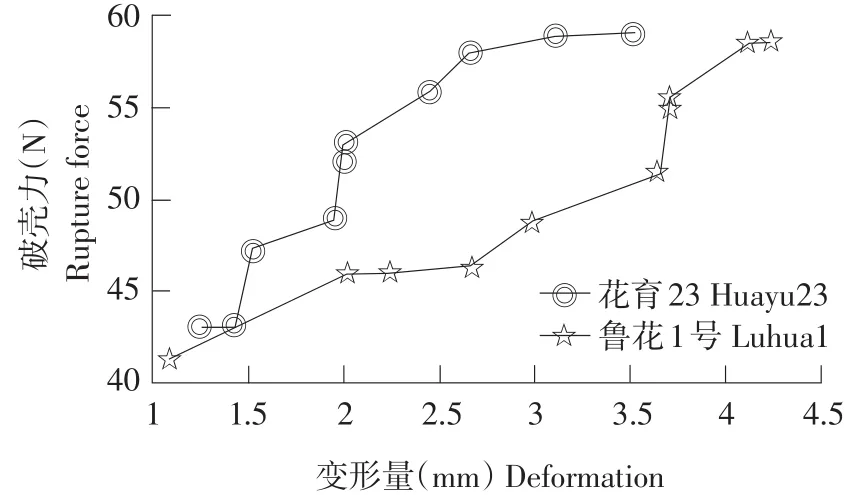
图10 品种对破壳力与和形量影响Fig.10 Effects of varieties on rupture force and deformation

2.3 创建接触形式

通常接触问题可以分成两大类：刚体—柔体接触和柔体—柔体接触。花生种子力学试验分析中，接触部件刚度大于花生壳刚度，将花生种子破壳接触形式定义为刚体—柔体接触。

2.4 花生种子弹性模量

固体农业物料力学性质同金属材料有相似之处。因此，计算公式和力学指标同金属材料表达方式一致[16]。

花生种子弹性模量是脱壳过程中重要参数，弹性模量与含水率有关。根据花生种子在载荷下受力与变形关系，计算出其应力和应变为：

式中，σ-应力（MPa）；F-试件所受轴向力（N）；S-试件横截面积（mm2）。

式中，ε-试件发生应变；ΔH-试件破损时实际变形（mm）；H-试件原有高度（mm）。

由式（5）和（6）得花生种子弹性模量为：式中，E-弹性模量（Mpa）。

选取不同含水率鲁花1号花生种子计算，获得不同含水率对应弹性模量（见表8）。

图11 花生种子三维模型Fig.11 Three dimensional model of peanut seed

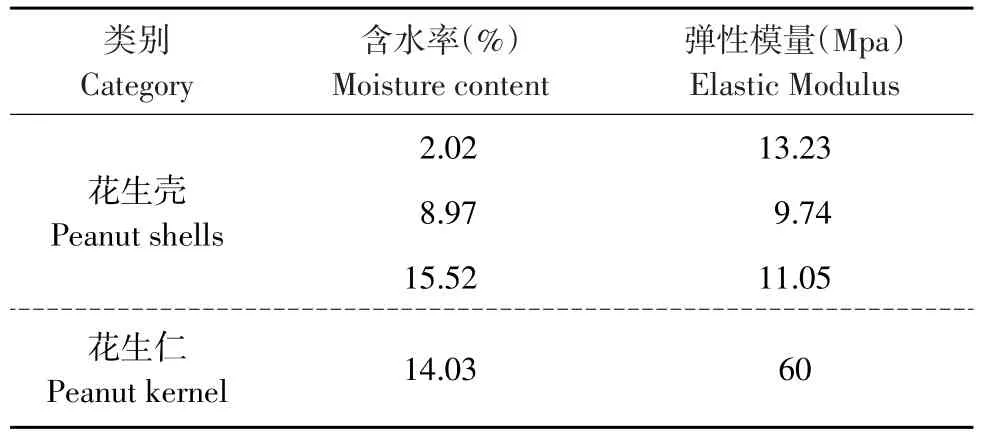
表8 花生种子不同含水率弹性模量Table 8 Elastic modulus of different moisture content of peanut seed

3 花生种子有限元模型

有限元法（Finite element method，FEM）计算中，常将整体离散成多个网格单元分析，依据极限逼近思想，用有限未知量逼近真实物理系统。单元内部各点位移用单元节点表示，当给定单元任意未知变量位置时，即可用形函数和相应节点值计算该点位移。张永生等建立土体稳定性有限元模型，解决土体稳定性弹塑性变形问题[17]。假设平面上任意一个节点单元分别用i，j，k表示，单元节点中x和y方向位移分量分别为u和v，节点处形函数分别为Si，Sj和Sk，节点位移分量分别为Uix，Uiy，Ujx，Ujy，Ukx，Uky，则节点单元中应变能和位移分别为[18]：

式中，Ue为应变能，J，ε为应变矩阵，V为单元体积（mm3）。

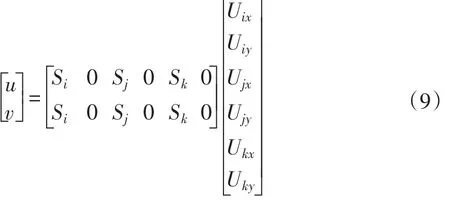
对于平面应力问题，物体内任意一点应变状态可用3个独立变量表示：

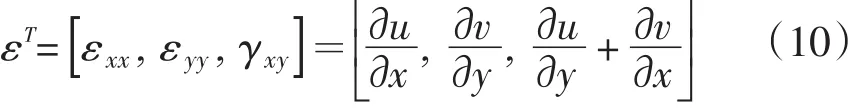
式中，εT为花生种子内任意一点应变矩阵转置，εxx，εyy为应变分量，γxy为切应变。

花生种子在压缩过程中，等效应力符合第四强度理论，设σi，σj，σm为每个单元三个主应力，则花生种子等效应力为：

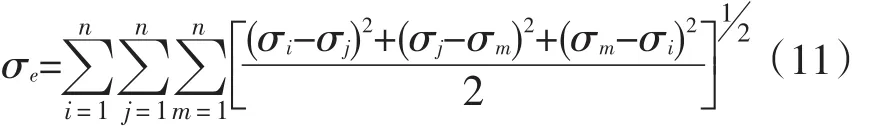
式中，σe为等效应力，n为单元总数。

在对有限元静力学仿真时，难点在于非线性方程组求解，钱巍等利用预处理共轭梯度算法解决有限元中线性方程组求解[19]，而在有限元求解时，实质是拉格朗日方程泛函问题，通过变分原理和插值函数求出数值解[20]，求解误差精度与划分单元尺寸有关。因此，给出花生种子有限元计算最优收敛准则。

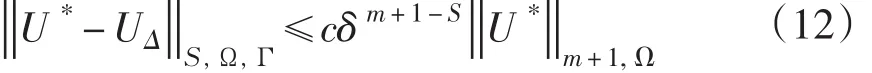
式中，U*为精确解；UΔ为有限元解；C为常数；δ为单元尺度；S，Ω，Γ为有限单元边界条件；m为场函数最高导数阶数。

4 花生种子有限元仿真

由于花生种子物理模型与实体存在误差。因此，有限元仿真时，需对非主要因素简化处理。本文在花生种子有限元仿真中，假设花生种子含水率和温度为定值；开始施加载荷时，花生种子应力为零；花生壳和花生仁分别等效于各向同性材料；不考虑其内部结构对花生壳影响。加载方式为正放加载、侧放加载和立放加载。网格划分时，设置单元类型为solid 186，自动划分网格，花生壳网格单元为4670，花生仁网格单元为12525。花生壳弹性模量为9.74 Mpa，花生仁弹性模量为60 Mpa，泊松比为0.4，仿真时间设置为1秒，网格划分结果如图12所示。

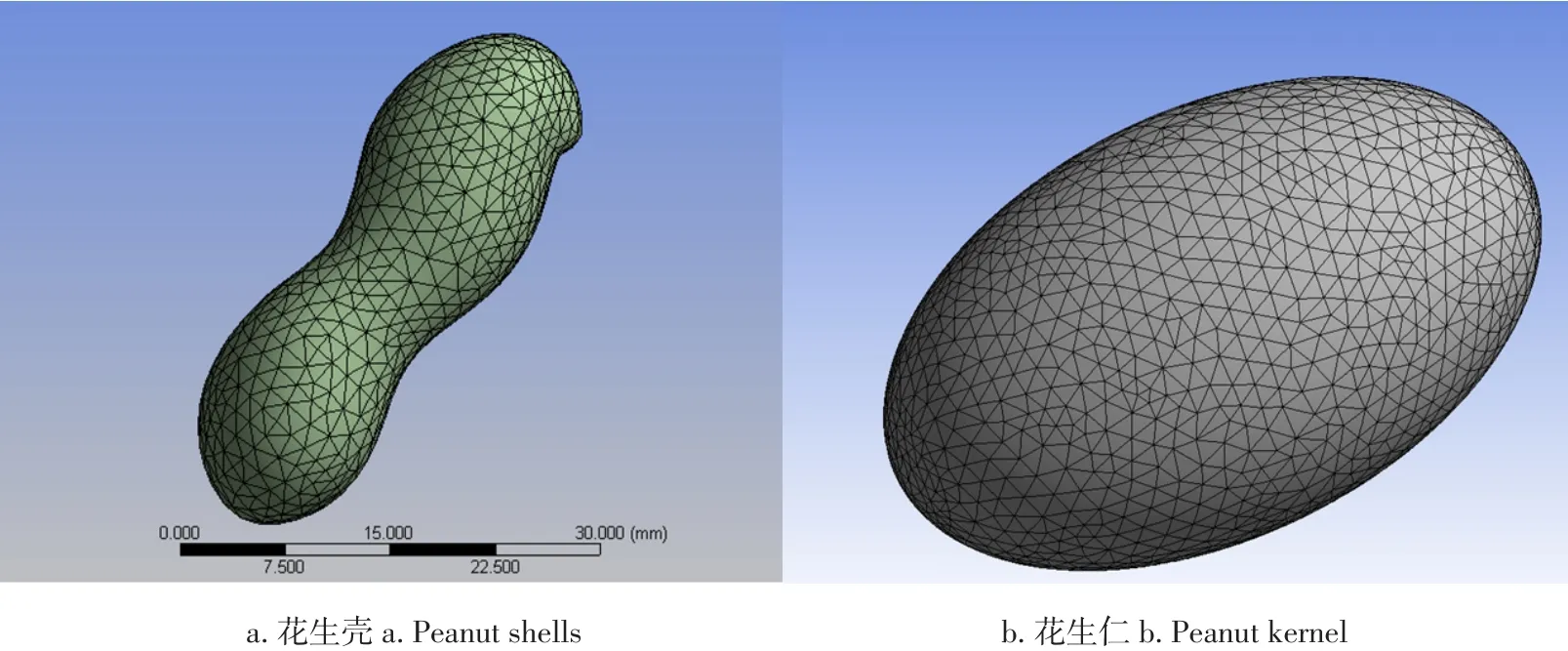
图12 花生模型网格划分Fig.12 Peanut model grid division

4.1 花生壳有限元分析

花生壳有限元分析结果见图13，由图a，c，e压缩位移变化云图可知，花生壳从不同方向施加载荷时，压缩位移沿受压中心以一定梯度向四周扩散，强度逐渐降低，最大压缩位移在花生壳受压中心处，且最大压缩位移分别为2.34、3.23和3.86 mm。图b，d，f反映不同加载方式时，花生壳等效应力（VonMises Stress）变化云图。由图b，d，f可知，花生壳在不同方向加载时，其抵抗材料应力强度等效应力沿载荷加载方向扩展，等效应力最大值在受压点棱边处，说明在受压过程中，随加载时间增加，花生壳等效应力不断增大，当等效应力达到材料应力极限时，产生裂纹，且沿着等效应力最大区域破裂。

为了解花生壳在加载过程中位移变化形式，涉及花生壳内部位移场局部流线，如图14所示。花生壳在施加载荷时，内部位移沿受压中心以一定梯度向四周辐射，强度逐渐降低。所以花生壳在受压时，受压区域位移变化量最大。图15为不同加载方式下，变形量等势值与加载时间变化关系。

由图15可知，在相同加载时刻，变形量等势值为立放加载＞侧放加载＞正放加载。因为载荷与花生壳接触面积越小，内部产生等效应力越大。说明在相同载荷情况下，立放加载变形速度最快，最易破壳。图16为花生破壳之前，压缩载荷与变形量关系。

由图16可知，随着压缩载荷增加，变形量增加，压缩载荷与变形量之间存在非线性关系，试验结果与有限元计算结果基本吻合，相对误差为6.16%。其相对误差可由式（13）计算：

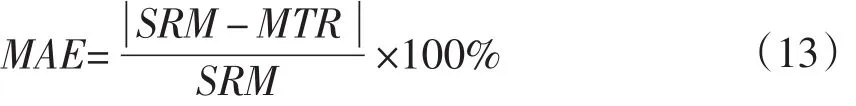
式中，MAE-相对误差；SRM-变形量均值仿真结果；MTR-变形量均值试验结果。

4.2 花生仁有限元分析

由于花生壳和花生仁材料属性不同，其受压破损特性差异较大。花生仁有限元分析结果如图17~18所示，由图17可知，从顶部施加载荷，花生仁受压变形呈多边形向四周延伸，由于花生仁弹性模量比花生壳弹性模量大约6倍，因此，在相同加载方式和载荷条件下，其最大变形量约为花生壳32%，且受压中心处变形量最大，最大值为1.24 mm。

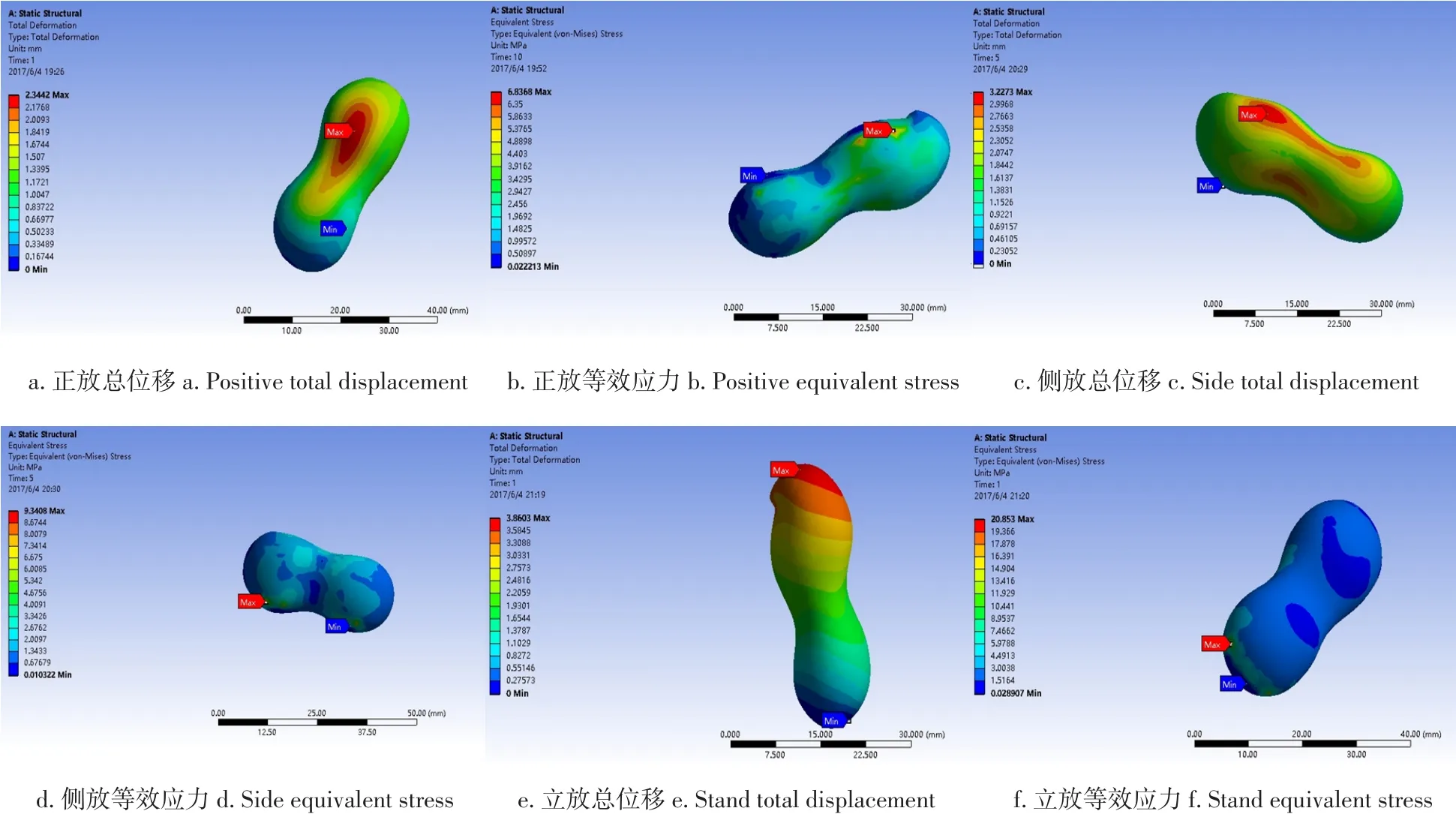
图13 花生壳有限元分析结果Fig.13 Results of finite element analysis of peanut shells

图14 花生壳内部位移场流线Fig.14 Flow chart of the displacement field inside the peanut shell

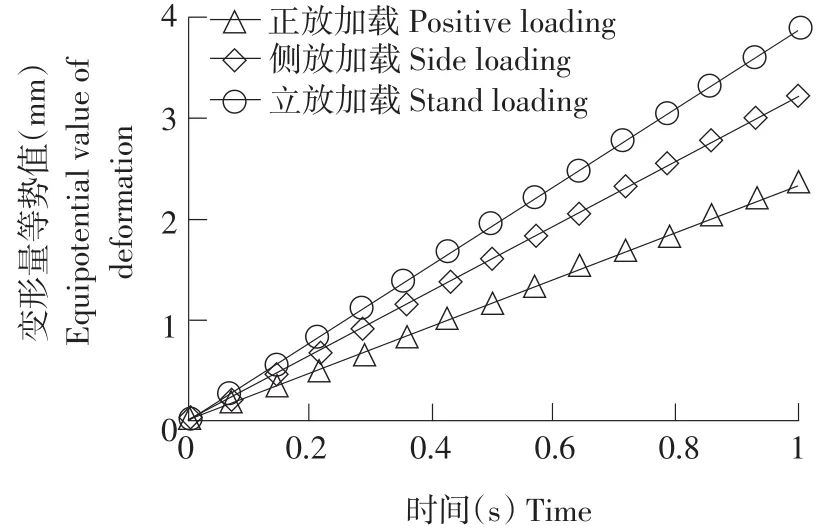
图15 变形量等势值与仿真时间关系Fig.15 Relationship of displacement equipotential and time

图18 为花生仁截面等效应力剖面云图，由图18可知，花生仁内部等效应力在加载区域较大，中间较小。因时，花生仁从顶端裂成两瓣。花生仁不同加载方式变形量等势值与加载时间变化关系见图19。

由图19可知，立放加载最大变形量大23.3%，试验初期，立放加载变形量变化率快于正放加载。因为花生仁在压缩过程中，立放加载接触面较正放加载接触面小。因此，立放加载更易使花生仁破裂。

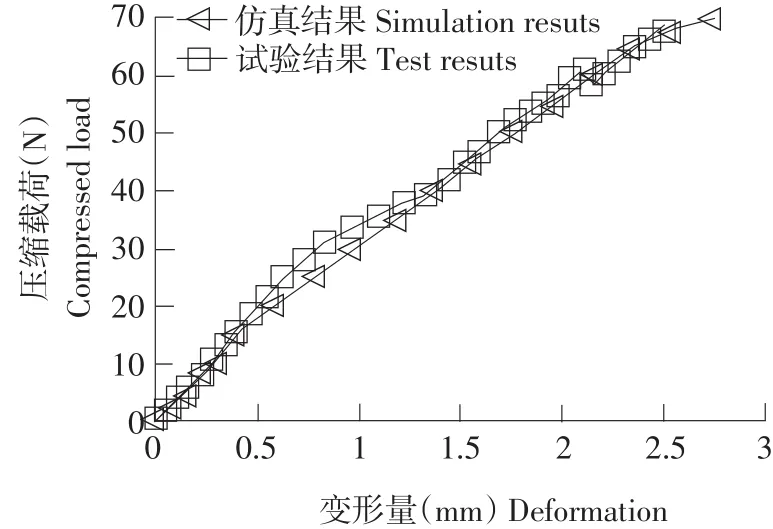
图16 压缩载荷与变形量关系Fig.16 Rlationship of compression load and displacement

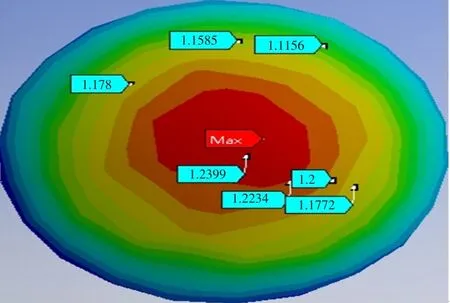
图17 花生仁受压位移等势值云图Fig.17 Peanut kernel displacement equipotential value cloud map

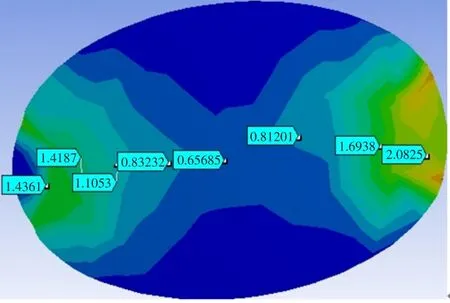
图18 花生仁等效应力截面云图Fig.18 Peanut kernel equivalent stress section cloud map

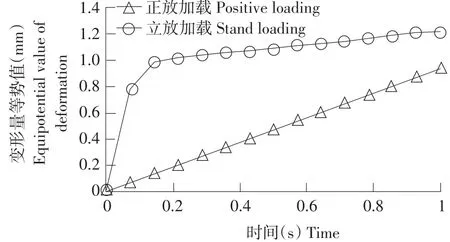
图19 花生仁变形量等势值与仿真时间关系Fig.19 Relationship of deformation equipotential and time

5 讨 论

花生种子脱壳是种子加工重要环节，脱壳特性对花生种子脱壳设备设计具有理论价值。因此，深入研究花生种子受力变形和等效应力对优化脱壳设备关键部件，降低脱壳损伤具有重要意义。

花生种子加载速度、含水率、加载方式和品种对破壳力有显著性影响，直接影响脱壳效果。杨亚洲等研究加载方式和含水率对花生壳及花生仁破壳力影响，结果表明含水率和加载方式对破壳力影响显著，与本研究结果一致[21]。易克传等研究含水率对花生壳和花生仁破壳力影响，结果表明随含水率增加，破壳力相应增加，与本研究结果一致[22]。本研究与王京等研究花生仁力学特性及有限元仿真结果存在差异[14]，由于花生种子脱壳过程中力学特性复杂，其脱壳过程中碰撞力学特性等相关问题有待进一步研究。

6 结 论

a.本研究以辽宁地区主产花育23和鲁花1号为试材，破壳力和变形量为试验指标，通过单因素试验研究加载速度、含水率、品种及加载方式对花生种子脱壳特性影响。研究结果表明，加载速度增加25%时，破壳力和变形量下降7.54%及2.11%，含水率增加6.6%时，破壳力和变形量上升19.7%及8.5%。相对于正放加载，立放加载更易破壳；鲁花1号和花育23对比中，鲁花1号更易破壳。

b.建立花生壳和花生仁有限元模型，采用ANSYS软件对其静力学仿真。仿真结果表明，花生壳在不同加载方式下，立放加载变形量最大，最大变形量为3.86 mm；等效应力沿受压中心向棱边延伸，变形量与压缩载荷之间存在非线性关系，得出变形量等势值与仿真时间数值解，花生仁最大变形量为花生壳32%。变形量仿真结果与试验结果基本一致，相对误差为6.16%。

[1] 高连兴,陈中玉,Charles Chen,等.美国花生收获机械化技术衍变历程及对中国的启示[J].农业工程学报,2017,33(12):1-9.

[2] 那雪姣,刘国明,张文,等.机械脱壳时花生仁损伤特征及规律[J].农业工程学报,2010,26(5):117-121.

[3] 吕小莲,胡志超,于向涛,等.花生种子挤压破碎机理的试验研究[J].华南农业大学学报,2013,34(2):262-266.

[4] 王京,高连兴,刘志侠,等.典型品种花生种子尺寸及均齐性研究[J].华中农业大学学报,2016,35(5):131-136.

[5] Dilmac M,Altuntas E.Selected some engineering properties of peanut and its kernel[J].International Journal of Food Engineering,2012,8(2):1168-1174.

[6] Balasubramanian S,Shama R,Sardana V.Studies on some engineering properties of peanut pod and its kernel[J].Journal of Agricultural Engineering Research,2011,48(2):38-42.

[7] Fasina O O.Compressibility and physical properties of peanut hull grinds[C].2007 Minneapolis,Minnesota,2007.

[8] Aydin C.Some engineering properties of peanut and kernel[J].Journal of food Engineering,2007,79(3):810-816.

[9] Bitra V S P,Banu S,Ramakrishna P,et al.Moisture dependent thermal properties of peanut pods,kernels,and shells[J].Biosystems Engineering,2010,106(4):503-512.

[10] 史建新,赵海军,辛动军.基于有限元分析的核桃脱壳技术研究[J].农业工程学报,2005,21(3):185-188.

[11] 张荣荣,李小昱,王为,等.基于有限元方法的板栗破壳力学特性分析[J].农业工程学报,2008,24(9):84-88.

[12] 张克平,黄建龙,杨敏,等.冬小麦籽粒受挤压特性的有限元分析及试验验证[J].农业工程学报,2010,26(6):352-356.

[13] 李震,俞国胜,曲迪.基于ANSYS的生物质液压成型机双锥度模具特性研究[J].东北农业大学学报,2013,44(11):132-136.

[14] 王京,高连兴,刘志侠,等.典型品种花生米静压力学特性及有限元分析[J].沈阳农业大学学报,2016,47(3):307-313.

[15] Iraj B,Sayed H P,Fatemeh R.Mechanical behavior of peanut kernel under compression loading as a function of moisture contents[J].Elixir Agriculture,2011,36:3552-3557.

[16] 徐对来,魏晓东,刘磊,等.固体农业物料力学特性的研究[J].黑龙江八一农垦大学学报,1998,10(3):40-44.

[17] 张永生,刘庆华.大变形有限元法计算水闸地基稳定性基本原理[J].东北农业大学学报,2006,37(2):232-234.

[18] 李心平,高连兴,马福丽.玉米种子力学特性的有限元分析[J].农业机械学报,2007,38(10):64-72.

[19] 钱巍,张燕晖,迟媛.机群环境下基于PCG法的有限元并行算法[J].东北农业大学学报,2006,37(3):390-392.

[20] 杨咸启,李晓玲.现代有限元技术与工程应用[M].北京:北京航空航天大学出版社,2007.

[21] 杨亚洲,刘姗姗,杨立权.花生荚果及花生仁力学特性试验研究[J].中国农机化学报,2016,37(10):108-111.

[22] 易克传,张新伟,沈永哲,等.含水率对花生脱壳及花生仁破壳力学性质的影响[J].扬州大学学报:农业与生命科学版,2013,34(3):65-69.

Experimental and finite element simulation of typical peanut seeds shelling characteristics/

HOU Junming,YANG Yong,DONG Shuai,HE Tao,BAI Jingbo,LI Jinpeng
(School of Engineering,Shenyang Agricultural University,Shenyang 110866,China)

In order to study the deformation and equivlent stress for peanut seeds during the processe of mechanical shelling,and improve the design of the shelling equipment,the single factor tests of peanut seeds were conducted.Two kinds of peanuts that cultivated in Liaoning Huyu 23 and Luhua 1 were selected as tested objects.The rupturing force and deformation were selected as the test indexes,the loading velocity,moisture content,loading method and variety as the influence factors.Based on ANSYS software,finite element model of peanut shell and peanut kernel were set up,and conducted static simulating for it.The results showed that the loading rate,moisture content,loading method and variety had significant influence on the rupturing force(p＜0.05);as the loading velocity increased by 25%,the rupture force and the deformation decreased by 7.54%and 2.11%;as the moisture content increased by 6.6%,the rupture force and the deformation were increased by 19.7%and 8.5%.The maximum deformation of peanut shell with different loading methods of in finite element simulation were 2.34 mm,3.23 mm and 3.86 mm,the relation between deformation and compressive load was nonlinear.The maximum deformation of peanut kernel was approximately 32%of peanut shell deformation.The simulation results were near to the experimental results.This study will providereference data for further improving the performare of peanut shelling machinekey components and reducing shelling damage.

peanut;mechanical property;finite element;compression test;ANSYS

S565.2

A

1005-9369（2017）11-0074-12

时间2017-12-7 12:38:36 [URL]http://kns.cnki.net/kcms/detail/23.1391.S.20171207.1238.016.html

侯俊铭,杨勇,董帅,等.典型花生种子脱壳特性试验及有限元仿真研究[J].东北农业大学学报,2017,48(11):74-85.

Hou Junming,Yang Yong,Dong Shuai,et al.Experimental and finite element simulation of typical peanut seeds shelling characteristics[J].Journal of Northeast Agricultural University,2017,48(11):74-85.(in Chinese with English abstract)

2017-08-22

国家自然基金项目（51475312）；中国博士后基金（2012M510077）

侯俊铭（1978-），男，博士，副教授，研究生导师，研究方向为农业机械设计与制造。E-mail:junming_hou@163.com