让探究成为习惯 使学习更加自然
——以“等比数列的前项n和”教学为例
吴新建
(江苏省张家港市沙洲中学 215600)
1 问题的提出
苏霍姆林斯基说:“在人的心灵深处,都有一种根深蒂固的需要,这就是希望感到自己是一个发现者、研究者、探索者.在儿童的精神世界中,这种需要特别强烈.”[1]笔者认为,学生的数学学习活动不应只限于接受、记忆、模仿、和练习.高中数学课还应引导学生进行自主探究,动手实践等学习活动.应将数学探究活动植根于日常教学活动中,让更多的教学环节渗透探究的元素、探究方法、探究思想.让数学探究真正成为学生学习的习惯. 这样才能真正改变学生的学习方式,提高学生的创新能力.
等比数列的前n项和公式的教学是高中数学的经典内容.推导公式的典型方法-“错位相减法”是高中阶段数列求和的基本方法之一.笔者曾听过该内容多节次的教学观摩课,虽有不少老师在课上也尝试通过一些方式引导学生探究错位相减法,但效果似乎大多不太理想,最终大多还是教师直接“告知”或学生自己看教材得知.这样的方式让学生觉得很不自然, 也不是真正的探究学习.如何让学生更自然地自主探究发现错位相减法是教学的难点.下面笔者结合自己设计的一节以猜想发现为先导的“等比数列的前n项和”探究教学为例,就如何让探究教学更加真实自然,谈一些肤浅认识,仅供同行参考.
2 教学设计及意图
2.1 梳理旧知,提出问题
以表格的形式让学生梳理等差、等比数列的有关概念及性质,并提出以下问题.

等差数列等比数列1. 定义an-an-1=d(n≥2)anan-1=q(n≥2)2. 通项an=a1+(n-1)dan=a1qn-13. 性质由m+n=p+q⇒am+an=ap+aq由m+n=p+r⇒am·an=ap·aq4. 前n项和公式:Sn=n(a1+an)2=na1+n(n-1)2d推导方法:倒序相加
问题1从表中可知,等比数列中还有什么内容需要研究?
学生:等比数列的前n项和公式.
问题2类比等差数列的前n项和公式,你认为求等比数列的前n项和公式的目标是什么?
学生:用等比数列{an}的首项a1,末项an,公比q,项数n等基本量表示前n项的和Sn.
设计意图通过等差数列与等比数列的对比,一方面让学生通过类比的方式自然地提出需要探究的课题及目标.同时也培养了学生从数学内部提出问题的意识和能力.
问题3Sn=a1+a2+…+an中含有n个未知量,如何计算呢?
学生:可以利用通项公式an=a1qn-1,将其转化为仅含有三个未知量,即
Sn=a1+a1q+…+a1qn-1
=a1(1+q+q2+…+qn-1).
因此,要求Sn,只需求
Bn=1+q+q2+…+qn-1.
教师:如何求Bn呢?
教师:(学生思考后)逐项相加,行吗?
学生:项数少可以,项数多了不行.
教师:用推导等差数列的前n和的方法(倒序相加)行吗?
学生:不行,因为等比数列中ak+an-k+1≠a1+an,倒序相加后还是有很多不同的项.
学生:考虑到在等比数列{an}中,有ak·an-k+1=a1·an,可不可以将Bn倒序相乘呢?
教师:想法有一定的道理,请大家尝试一下看行不行?
学生尝试后, 发现Bn·Bn=(1+q+q2+…+qn-1)(qn-1+qn-2+…+q2+q+1)展开后远不止qk·qn-1-k这样的项,很难直接求出展开各项的和.探究陷入了困境.
教师:(故意带着怀疑的神情)等比数列的前n项和会有统一的公式表示吗?
设计意图教师有意稚化了自己的思维,提出一些学生在探究过程可能的一些想法,虽然教师明白这些方法不能推导出求和公式,但这些问题有利于引起与学生的思维共振,促进各层次学生的思维参与.同时,也让学生体会到数学探究过程需要不断的尝试,并不是每一次都能成功.
2.2 合情推理,发现公式
教师:当我们对一个数学问题的一般情形研究有困难时,我们常常可以从问题的特殊情形开始研究.
问题4如何将Bn=1+q+q2+…+qn-1进行特殊化呢?
学生:可以将公比q和项数n取一些特殊值.比如:q=1时,Bn=n.
教师:q=2时呢?设Tn=1+2+22+…+2n-1,再让n取一些特殊值,会得到什么结果?
学生:T1=1T2=3,T3=7,T4=15,T5=31, 归纳猜想:Tn=2n-1.
教师:那么可猜想Bn=1+q+q2+…+qn-1=qn-1了吗?
学生:q=3时显然就不成立.
教师:设Xn=1+3+32+…+3n-1,那么Xn与3n-1有什么关系呢?请完成下表1.
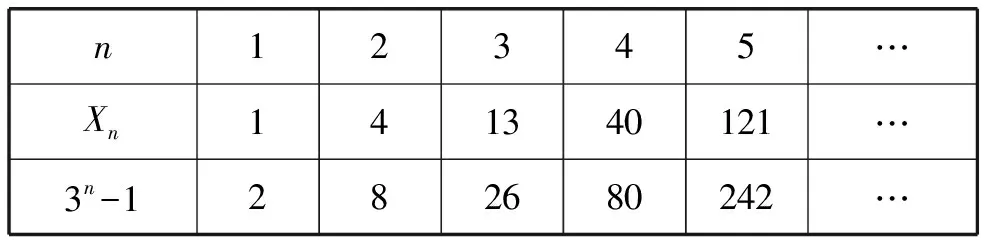
表1
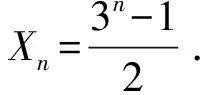
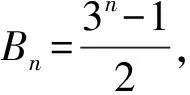

表2
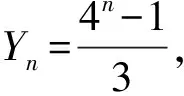
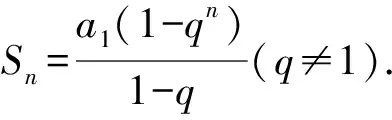
设计意图牛顿说:“没有大胆的猜想,就做不出伟大的发现”.由特殊到一般是数学发现的基本方法.通过对几个特殊的、简单的等比数列求和结果归纳出一般公式,一方面降低了思维的坡度,另一方面也培养了学生发现问题的意识.
2.3 演绎推理,证明公式
问题5现在可以用归纳出的公式去求等比数列的前n项和了吗?
学生:不行,因为这只是通过归纳猜想得到的,其正确性还需要严格证明.
问题6如何证明以上公式呢?
学生:当q=1时,Sn=na1显然成立.
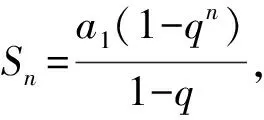
只要证明:Sn(1-q)=a1(1-qn),
要得到上式,只需将等式
Sn=a1+a1q+…+a1qn-1
①
两边同时乘以公比q,得
qSn=a1q+a1q2+…+a1qn-1+a1qn
②
将①式减②式即得Sn(1-q)=a1(1-qn).
教师:①式右边有n-1项与②式右边的n-1项“错位”相同,两式相减时相同的n-1项就消去了,我们将这样的方法称为错位相减法.
设计意图问题5对教师和一些思维比较严密学生来说,答案显然是否定的,但对一些逻辑思维不是很严谨学生来说,也许就认为公式可以直接用了.教师再次通过稚化思维的方式提出问题,目的是让学生将错误的思维充分暴露出来.
2.4 回顾小结,反思再发现
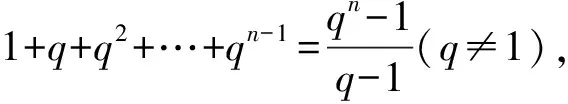

教师:将以上两个等式左边推广到一般情形即:(q-1)(1+q+q2+…+qn-1),将其展开后的结果为qn-1,因此,等比数列的求和公式实质是源于一个恒等式:(q-1)(1+q+q2+…+qn-1)=qn-1, 这正是错位相减法的本质所在.
设计意图将错位相减法与学生头脑中已有知识与方法联系起来,目的是适当降低学生理解错位相减法的突兀感,有助于学生形成更加完整、和谐的知识结构.让新知识的学习变得更加自然.
2.5 公式应用及课堂小结(略)
3 让探究活动更自然的几点教学建议
高中数学人教A版主编寄语:“数学是自然的,清楚的”,数学概念、数学方法与数学思想的起源与发展都是自然的,它们是水到渠成的浑然天成的产物.[2]因此,基于数学学科自身特点的探究学习过程不是强加于学生.教师应引导学生研究探究对象背景、形成过程及与其他对象之间的联系. 让学生真正经历探究的过程,这样探究活动才是真实且自然的.下面笔者就如何让探究活动更自然谈几点建议.
3.1 选择的探究内容要自然
并不是所有学习内容都需要用探究学习的方式来进行,接受学习也是必要的.因此,数学探究首先要选择好适合探究的对象,不能为探究而探究,让探究成为课堂的“标签”.要让学生感到提出的探究内容是自然的,必要的.同时,探究内容难度要适当.内容太简单,学生会觉得没有探究的必要,不能激发学生探究的兴趣;内容太难,学生感到无从下手,失去探究的信心.探究内容的选择要让大多数学生做到“跳一跳能摘到”.这样才能让更多学生参与到探究活动中来.
以本节课为例,如果设计成一开始就直接让学生探究一般等比数列的求和公式,这对大多数学生来说是很困难的,探究活动很难进行下去.而先从一些特殊的等比数列的前n和的结果去归纳猜想发现公式,再结合公式的特点去寻找证明公式的方法,则要容易得多,这样也有利于提高学生探究学习的信心.
3.2 创设的探究情境要自然
探究的情境既可以从生活情境中抽象出来,也可以从数学内部产生.其作用除了能够激发学生的探究兴趣,让学生产生探究的必要性以外,还应在探究活动进一步展开中对学生的探究起到导向作用,这样的情境才更加符合学生的认知规律,才能让学生觉得更加真实、自然.
以本节课为例,不少教师喜欢选择一个生活中等比数列的求和问题作为问题情境,如国际象棋发明者与国王的故事等.笔者认为,这样的情境的确可以用来说明研究等比数列求和公式的必要性,但对进一步探究求和公式的作用不大,而且对一个已具备一定理性思维的高中学生来说,这样情境似乎过于做作,不能真正激发学生的探究欲望.而从等差数列与等比数列知识体系和研究方法一致性角度提出等比数列的求和问题,则会让学生感觉更自然,且有利于培养学生通过类比方式去提出问题和解决问题的意识.而探究活动开始前让学生梳理等差、等比数列概念、性质及方法也有助于学生发现推导求和公式方法.这正是笔者设计教学环节2.1的意图.
3.3 设计的探究过程要自然
探究过程的设计要充分体现知识发生发展及学生心理认知的过程,并能促进学生有效参与探究活动.在教学设计时,要充分预设学生可能的探究方向,对教学过程中学生出现的一些“意外”想法即使不能探究成功,也要分析其合理的因素并给予肯定和鼓励,要保护学生探究的积极性.这样才能让探究的过程更加真实、自然.
比如在本课例中,学生提出将等比数列前n项和倒序相乘后求和,这样的想法虽然不能得到求和公式,但学生能从等差数列的倒序相加求和类比到等比数列的倒序相乘求和,体现了其通过类比进行合情推理的意识.法国数学家、天文学家拉普拉斯(Laplace, 1749—1827)说:“甚至在数学里,发现真理的主要工具也是归纳和类比.”[3]这句话深刻说明归纳和类比等合情推理方式在数学探究中的意义.因此笔者没有过早打断学生的思路,而是及时肯定了他的想法,并给出一定时间让学生尝试.这样学生可以充分经历公式的探究过程.
3.4 提出的探究问题要自然
在数学探究中,探究活动首先是基于问题的活动,恰当的问题是促进学生进行探究的引擎,也是学生探究历程中的航标灯.因此,教师在设计探究的问题时要充分研究学生的认知水平,本着“惑学生所惑,难学生所难,错学生所错”的原则,提出符合学生思维状态的问题.为了让提出的问题更加符合学生课堂上真实的心理状态,“稚化思维”是教学中常用的一种提问策略和艺术.
所谓“稚化思维”,就是教师有意识把自己的思维降格到与学生想仿的水平,退回到初学者的状态,设身处地地揣摩学生的认知状态,在此基础上因势利导,实现师生“思维共振”的一种教学艺术[4].本节课中笔者多次采用“稚化思维”方式提出了学生在探究公式过程的可能想法,有效地促进了学生的思维的参与,让整个探究过程显得更自然、流畅.
——由倒序相加想到倒序相乘

