揭示解题方法的数学本质 改进数学解题教学
孔德宏 贺政刚
(云南师范大学数学学院 650092)
在中学数学解题教学中,教师往往只是讲了一道题的多种解法,而对为什么可以这样解(解法的依据),以及解法的数学本质往往揭示得不够,呈现出课堂解题教学热热闹闹、方法多样的表象.但这样的解题教学事实上却是低效甚至无效的,本质上也是有害学生学习的.本文以一个问题(已知一条二次曲线,求一次式的最值)的三种典型解法为例,谈谈数学解题教学中如何揭示解法的数学本质,从而改进数学解题教学.
问题已知x2+y2-xy=3,求2x+y的最大值.
分析由于条件是一个二次式,很难把这个二次式直接代入目标式.于是大体有两种思路:一是令2x+y=t,把该一次式反向代回条件消y,得到关于x的二次方程,进而用判别式法求t的最大值;二是改变看问题的角度,想办法转化条件,使之可以正向代入目标式子中,以达到消元的目的,进而解决问题.正向代入又有两种思路:一是借助余弦定理;二是借助坐标变换.
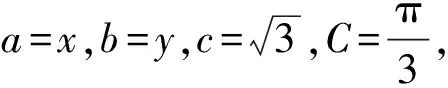
由正弦定理
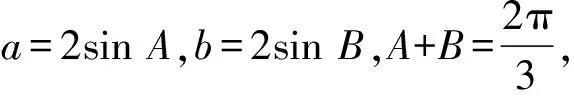
于是
2a+b=2·2sinA+2sinB
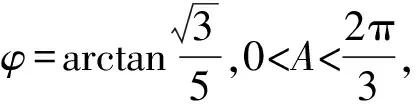
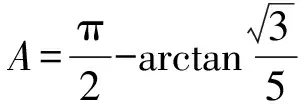
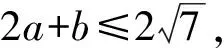
评析由于条件是一个二次式,很难把这个二次式直接代入目标式子.于是根据条件的结构,创造性地使用余弦定理,把一个一般的代数问题转化为解三角形问题.接下来使用正弦定理,把条件“直接正向”代入目标式子,达到了消元的目的,最后解决问题.
对于解法1,学生一方面感受到了知识间纵横联系之美,方法之妙外,也许还会有一些疑虑和顾忌:还有没有其他情形?这样解会不会用特殊代替了一般?
变式不妨把问题改为已知x2+y2-xy=3,求y-x的最大值.
仍然沿用解法1的解法,则
y-x=b-a
=2sinB-2sinA
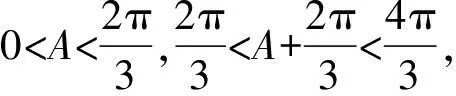
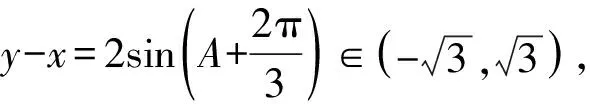
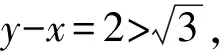
事实上,用解法1来解本类问题有很多的局限,比如,为了使用余弦定理,条件就必须是二次齐次式等于常数的形式,即形如mx2+ny2+pxy=q的式子.
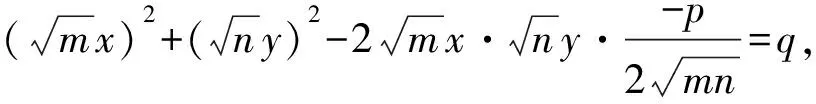
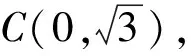
解法2(判别式法)令2x+y=t,
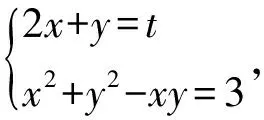
消y得7x2-5tx+t2-3=0
①
因为①式是关于x的二次方程,并且有实数解.
所以Δ=(-5t)2-4×7×(t2-3)≥0,
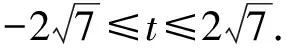
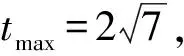
评析直接把条件正向代入目标式子很困难,这里逆向思维为之,令2x+y=t后,把目标反向代入条件消y,得到关于x的二次方程,进而用判别式法求t的最大值.
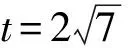
上述思考看起来很有道理,但事实上果真如此吗?答案是否定的,解法2是完全正确的.
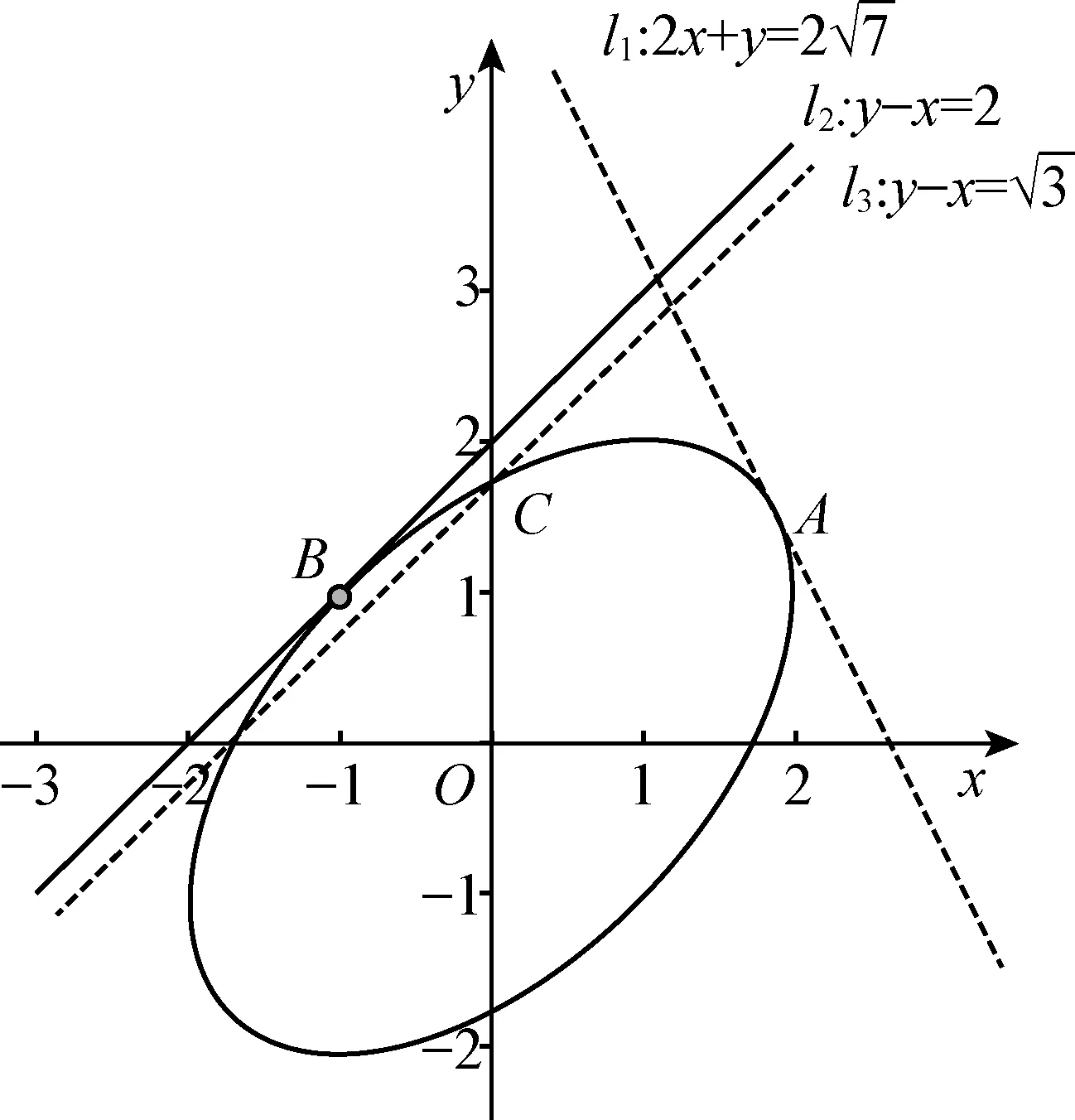
我们不妨从解析几何的角度进行分析:
在平面直角坐标系xOy中,2x+y=t为一组平行直线,记为l;x2+y2-xy=3为一条圆锥曲线,记为τ.由解析几何的知识知l与τ有交点的充要条件为方程①有实数解,进而等价于Δ≥0,且此时交点的横坐标x一定在自然定义域D上.所以,上述思考中的检验是多余的,也就是说今后在已知二次曲线,求一次式的最值时,只需用Δ≥0解出即可,并不需要检验.
另一类易犯的错误如果教师在解法2的教学过程中,不说清楚为什么不需要考虑x的限制条件的本质原因,那么这又会带来另一类错误,即无视x的取值范围,比如我们对题目进行一点改变:已知x2+y2-xy=3,且-1≤x≤1,求2x+y的最大值.
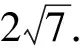
令f(x)=7x2-5tx+t2-3,则问题转化为f(x)在[-1,1]有解,求t最大值.
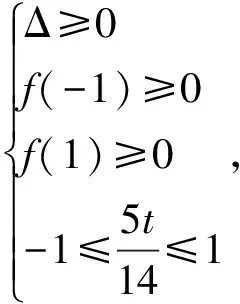
解得-4≤t≤4,故t的最大值为4,即2x+y的最大值为4.
所以教师在解法2的教学过程中,应对x的取值范围的作用进行深入揭示,并概括出结论:当二次曲线的x的范围为自然定义域时,我们可以直接用Δ≥0求出t的范围;当二次曲线的x的范围不是自然定义域时,在设出t后,通常要用二次方程根的分布加以解决.
解法3(坐标变换+三角换元)令
②
的最大值.
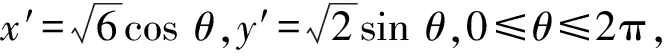
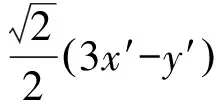
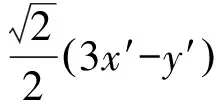
评析问题中的二次曲线含交叉乘积项,而通过坐标变换②,使得交叉项消失了,接下来就可以利用三角换元法快速得到答案,解法不得不说是很精彩的.但这样的解题教学,除了让学生感到数学是从天而降的,神奇、难学和不解外;除了让学生对教师能想出这样的解法而感到膜拜外,并没有任何教学价值.为什么可以这样换元?一定要这样换元吗?学生一点也不清晰,从而对这类问题的解题能力没有任何提升.
实际上解法3的背景是几何变换中的转轴变换.
我们知道ax2+bxy+cy2+dx+ey+f=0(a、b、c不同时为0)是平面xOy上的一条二次曲线.当b≠0时,总可以通过转轴变换
③
将原坐标系xOy逆时针旋转角θ后得到新坐标系x′Oy′,从而消除交叉项.
将③式代入方程ax2+bxy+cy2+dx+ey+f=0,得到原二次曲线在新坐标系下的方程为F(x′,y′)=0,F(x′,y′)为关于x′,y′的二元二次多项式.其交叉项为
[(c-a)sin 2θ+bcos 2θ]x′y′.
令(c-a)sin 2θ+bcos 2θ=0,

④
选取满足④式的θ就能通过旋转变换③,使得交叉项消失.得
F(x′,y′)=a′x′2+c′y′2+d′x′+e′y′+f′=0
⑤
此时,通常a′,c′不能同时为0,否则就不能成为题目中的二次曲线了.
(1)若a′、c′均不为0,就可以对⑤式中的x′项、y′项分别配方,化成椭圆或双曲线型a′(x′+p)2+c′(y′+q)2=r′的形式,接下来就能用三角换元解决问题;
(2)若a′、c′中有一个为0,不妨设a′=0,c′≠0,就可以对⑤式中的y′项配方,化成c′(y′+q)2+d′x′+r′=0的形式.当d′≠0,则为抛物线型,接下来就可以直接把条件中的x′解出来,正向代入目标式子求解;当d′=0,化成c′(y′+q)2+r′=0的形式,题目通常不会出现这种情况,因为此时就无法求目标一次式的最大值了.
事实上,对于二次曲线,经过旋转变换得到⑤式,接下来再作一个坐标系的平移变换,也就是通过配平方后换元,则最终可以把二次曲线化成下列三种情形:λ1x2+λ2y2=λ3(椭圆型或双曲线型);λ1y2+λ2x=0(抛物线型);λ1y2+λ2=0(直线型).
总结在数学解题教学过程中,教师只有在自己理解通透的前提下,才能更好地启发学生弄清楚解法的来龙去脉,并提炼数学思想方法,突出数学本质.也只有这样的解题教学,才能确实提升学生的数学解题能力.反之,则会使学生一知半解,知其然而不知其所以然,这样的教学是非常有害的.

