建国以来高考数学试题演变分析与展望

郑雪静 陈清华

(1福建师范大学数学与计算机科学学院 350117；2泉州师范学院数学与计算机科学学院 362000)

今年是恢复高考40周年，数学作为高考的重要学科，也走过了40年的历程，回首40年高考，我们就建国以来高考数学试题的演变进行梳理，为即将到来的新一轮高中数学课程改革在命题与考试方面提供借鉴.

1 民国时期(1912-1949)高考数学简介

民国时期的高考大都是高校单独命题招考，类似于现在的自主招生．抗日战争时期的1938～1940年为适应战时需要，保证招生质量，曾实行三年的国立各院校统一招生，1941年因抗战形势紧迫被中止统一招生，之后部分高校采用联合招生，比如1947年南开大学、清华大学、北京大学三校实行联合招生．[1]这一时期的高考数学试卷多为用英文表达，这与当时的数学教育采用英文原版教材和使用英文授课有关系．考查内容包括：初等代数、平面几何和立体几何、三角函数、解析几何、高等代数等五部分，其中前三部分是必考内容，后两部分根据考生报考专业不同，考试题目会有差别．试题数目以一般考生能在规定时数内做完试卷为准(数学3个小时)[2]，比如1923年国立北京大学高考理科试卷[3]，该试卷共10道题，其中初等代数、三角函数、解析几何各3题，立体几何1题，相对于现在高考试题，其难度不大，主要考查基础知识和基本技能，考查的内容和方式相对单一.

例1【1923年高考国立北京大学卷·理6】

Ifα，β，care the roots of the equationx3-px2+qx-c=0，find the value ofα2+β2+c2．

解析：若α，β，c是三次方程x3-px2+qx-c=0的三个根，求α2+β2+c2的值．该试题属于初等代数问题，考查方程的根及相关运算．依题意α，β，c是方程的根，则(x-α)(x-β)(x-c)=0，将式子展开与x3-px2+qx-c=0进行系数对比，得α+β+c=p，αβ+βc+cα=q，再由α2+β2+c2=(α+β+c)2-2(αβ+βc+cα)，可得α2+β2+c2=p2-2q．

2 建国以来高考数学命题与考试方式简况

建国以来，高考数学主要是全国统一命题与省市自主命题两种命题形式．1949年大部分高校沿袭民国时期单独招考的方法，少数高校采用联合招生的形式．1950年和1951年的高考有分区(东北区、西北区、华北区、中南区、西南区、华东区)联考也有统一招考．[4]1952年到1965年维持了14年的全国统一命题制度，1966～1976年十年“文化大革命”取消高考，1977年恢复高考，当时由于来不及组织高考试卷命题，最终由各省市自主命题，1978年恢复全国统一命题．[5]直至1985年上海率先实行自主命题，2002年北京也实行自主命题．从2004年起，开始分省命题，以后分省自主命题的范围不断扩大，而到2016年全国26个省又回归全国统一命题，山东部分采用全国卷(山东高考数学自主命题)，北京、天津、上海、江苏、浙江五省市仍自主命题.

值得纪念的是1952年，那年是全国高等学校实行统一命题考试的第一年，它形成了高考制度的基本框架，开启了中国高考的时代[4]．那年的高考在8月15、16、17日举行，每个科目考试时间为1小时40分钟．每个考生必须参加8个科目的考试，具体考试科目和时间见表1．1952年高考录取时高校根据专业要求，按各科不同比例计分，但此方法不能很好地体现各专业特点．[6]因此，1954年高考科目设置成文、理两类，1955年改成文、理、农医三类，1964年再改成文、理两类．1978年恢复高考后也是按文、理两类进行科目设置，直至2014年上海、浙江率先进入高考文理不分科试点．

表1 1952年全国高等学校统一招生考试时间和科目

3 建国以来高考数学试题的演变

建国以来高考数学试题经历了多重演变，我们主要从题型与题量、试题的背景、试题的性质三个方面进行分析.

3.1 题型与题量的演度

以全国统考卷，有文、理卷的以理科卷为统计对象，就建国以来高考数学试卷[7]的题型与题量进行统计分析，见表2．

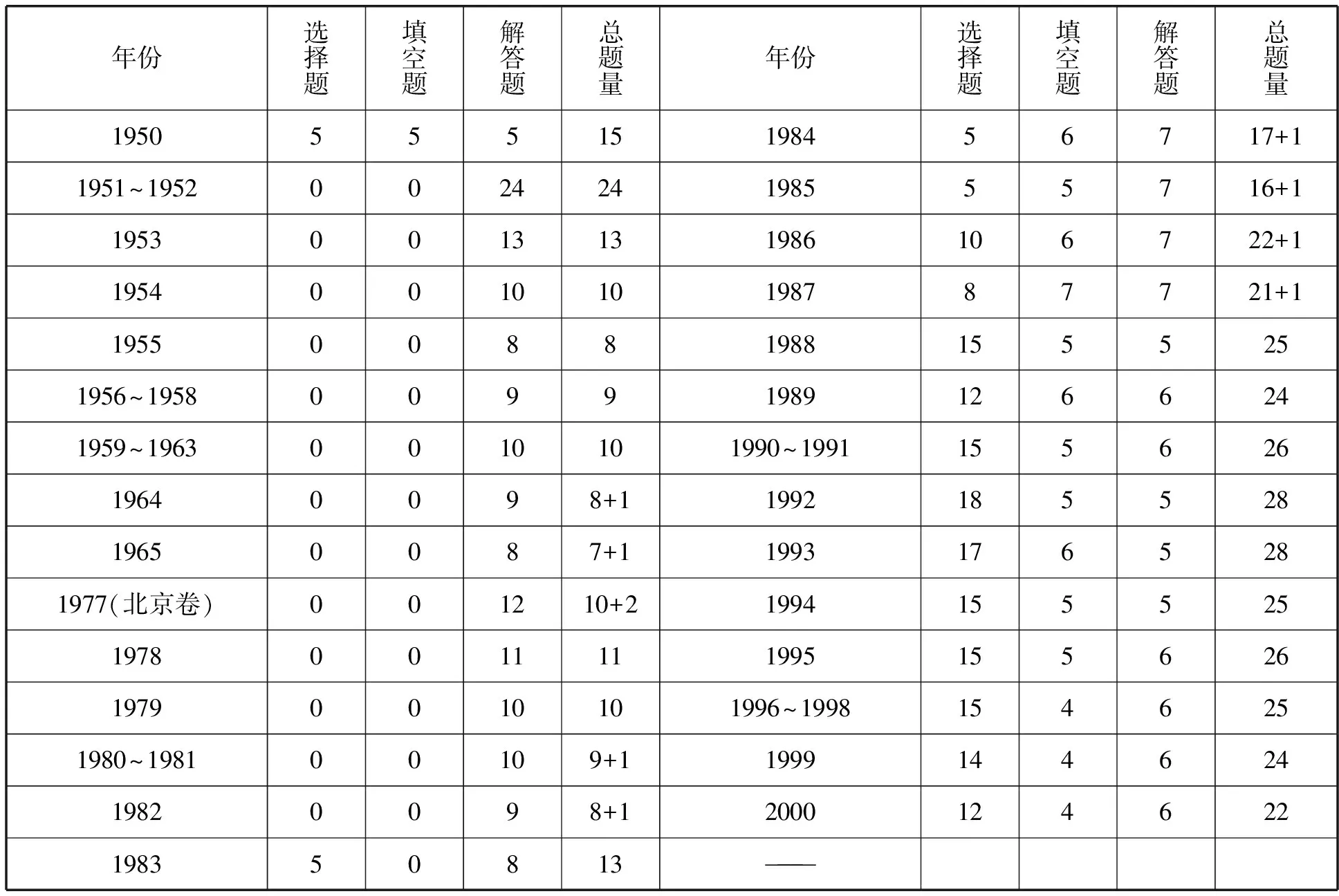
表2 建国以来全国高考数学试卷(理)题型与题量

表2显示，建国以来，高考数学试题有选择题、填空题、解答题三种题型．1950年高考数学试卷分为两组：甲组和乙丙组(类似于现在的全国Ⅰ、Ⅱ卷)，题目分为两部分：第一部分是5道单项选择题和5道填空题；第二部分是5道解答题．1951年和1952年也分为两部分，但题量达到24题．1953～1961年试卷一般由5道大题组成，有些大题再分小题，如第1大题以十个天干作为题名再设置甲、乙、丙、丁、戊、己、庚、辛、壬等小题，有些试卷有附加题．1951～1982年的试题都是解答题，题量一般在10道大题左右，到1983年开始有所增加，题量在13～28题之间，并且重新出现单项选择题，选择题题量在5～18题之间．1984年开始重新出现填空题，虽然1984～1988年试卷中第二大题没有明确是填空题，但题目只要求直接写出结果，因此我们把它当成填空题，题量在4～7题之间．2000年至今试题总量一般是22题，其中12道单项选择题、4道填空题、6道大题，有些大题有2～3个小题．特殊的，江苏省从2008年开始取消选择题．另外，1977年恢复高考后，有几年在高考试卷最后设置参考题或附加题，主要考查微积分知识，其成绩一般不计入总分，只作为招生时的参考.

3.2 试题背景的演变

高考数学试题背景的来源非常广泛，有教材背景、高等数学背景、竞赛数学背景、学科交叉背景、社会生活背景等等，我们从数学自身的性质出发，对建国以来高考数学试题从纯数学背景到应用数学背景的演变进行分析，同时对目前高考数学两类特殊背景：“数学阅读理解背景、数学文化背景”加以剖析.

(1)纯数学背景

建国后，我们主要学习苏联严谨、形式化的数学风格，这一时期的高考数学试题主要是纯数学背景，相比于现今高考数学试题，难度不大．在那个为实现“四个现代化”培养又红又专人才的年代，强调的是打好基础、掌握基础知识和基本技能，强调的是对概念的记忆和命题的理解，掌握证明和运算的技能．那时候是精英教育，1978年有610万考生，录取人数40.2万，录取率仅7%．[8]之后，为了提高区分度，数学试题的难度有所提高，有些试题内容甚至涉及微积分的知识．到了20世纪80年代初期，国际上对数学教育培养能力型、应用型人才的关注影响着我国，高考数学试题在1984年出现一个历史性转折，提出“出活题、考基础、考能力”的命题指导思想．[9]但主要还是一些纯数学背景试题，重点考查逻辑推理能力、数学运算能力、空间想象能力三大能力.

例2【1984年高考全国卷·理六(1)】

设p≠0，实系数一元二次方程z2-2pz+q=0有两个虚数根z1，z2．再设z1，z2在复平面内的对应点是Z1，Z2．求以Z1，Z2为焦点且经过原点的椭圆的长轴的长.

解析：该试题以一元二次方程、复数、椭圆等纯数学知识为背景，考查一元二次方程根与系数的关系、复数加减法几何意义、椭圆性质．由于p、q为实数，p≠0，z1，z2为虚数，因此Δ=(-2p)2-4q<0，即q>p2>0．由于两个虚数根z1，z2是共轭复数，所以它们在复平面内的对应点Z1，Z2会关于x轴对称，从而椭圆短轴在x轴上．又因为椭圆经过原点，因此原点为椭圆短轴的一个端点，从而短轴长为：2b=|z1+z2|=2|p|；

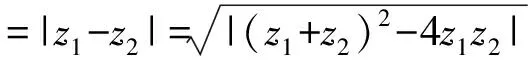
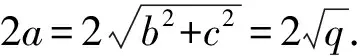
(2)应用数学背景

把数学应用当作实用主义、短视行为进行批判的情形，直到1990年代开始才有所改观．张奠宙先生曾指出：国内外的数学家多次评论我国学生考试成绩往往不错, 但一到写论文阶段就显得力不从心．这是我们数学教育上的一种通病，可能与我们的试题单一、纯数学化不无关系．1992年冬张奠宙、严士健、苏式冬走访了国家考试中心，建议在高考题中应该有一些应用题．他们说：这些年来，高考八股化的趋势并未得到遏制，[10]高考应该按照九年制义务教育数学教学大纲的要求：“要使学生受到把实际问题抽象成数学问题的训练，形成应用数学的意识．”[11]这与新一轮高中课程改革提出的数学教育的终极目标是一脉相承的．即：一个人经过数学教育之后，即便他将来从事的工作与数学无关，也会用数学的眼光观察世界，会用数学的思维思考世界，会用数学的语言表达世界．[12]建国以来的高考数学只是零星的出现一些应用背景的试题，比如1960年有一道求船与灯塔距离的问题，1979年全国高考理科卷有一道国防海岸线的问题(例3)，1995年高考全国卷理科卷第24题、文科卷第25题有一道关于淡水鱼养殖的函数模型问题．此后的高考数学试卷，或多或少均有一些应用背景的试题出现．1997年启动高中课程改革试点工作后，应用问题的形式更加灵活多样，背景更加丰富，在应用背景、试题设问方面都有所创新．2001～2007年新课程教育改革期间，增加了概率与统计知识，这一阶段主要以概率与统计内容为应用背景．之后，应用背景更注意源于社会、源于生活的真实情境[13]，使学生认识到数学来源于社会、生活，又应用于社会、生活中，把冰冷的数学回归生动、有趣、现实的情境中，更加有效地考查学生抽象、概括、建立数学模型的能力，体现数学的价值，提高学生分析问题和解决问题的能力.

例3【1979年高考全国卷·理五】

外国船只，除特许外，不得进入离我海岸线D里以内的区域．设A及B是我们的观测站，A及B间的距离为S里，海岸线是过A、B的直线，一外国船只在P点，在A站测得∠BAP=α，同时在B站测得∠ABP=β．问α及β满足什么简单的三角函数值不等式，就应当向此未经特许的外国船只发出警告，命令退出我海域？

图1

(3)两类特殊背景

①数学阅读理解背景

《普通高中数学课程标准(实验稿)》指出：高中数学课程还倡导自主探索、动手实践、合作交流、阅读自学等学习数学的方式．[14]这里强调了对学生数学阅读能力的培养，阅读理解背景试题成为近几年高考试题的一个亮点，这类试题一般结合文字语言、图形语言、符号语言进行叙述，题目比较长，信息量和阅读量一般比较大，考查学生阅读理解能力、语言转化和表达的能力，体现“多想少算”的理念，是对学生综合素质和能力的考查，成为高考的热点题型之一.

分析历年高考数学阅读理解背景试题，主要有以下几种类型：以教材内容为阅读材料，要求学生揭示所学内容的本质，掌握思想方法；呈现一些模拟学生解题过程的阅读材料，让考生判断解题过程的正误，正确的写出解题依据，错误的写出正确的解答过程；给定一些文字、图表的阅读材料，让考生通过归纳、探索，提取相关信息，发现规律，得出结论；提供新定义、新定理要求考生阅读后解决新问题．[15]或是由一些相互联系的条件组成的具有逻辑推理的背景，要求考生根据相关逻辑知识进行推理分析(比如2014年高考全国卷理科、文科第14题填空题：要求根据甲乙丙的陈述，推断乙去过的城市)．在信息化时代、大数据时代，从海量文字、数据、图表中进行阅读理解提炼是一项基本能力.

例4【2016年高考新课标Ⅰ卷·理16】

某高科技企业生产产品A和产品B需要甲、乙两种新型材料．生产一件产品A需要甲材料1.5kg，乙材料1kg，用5个工时；生产一件产品B需要甲材料0.5kg，乙材料0.3kg，用3个工时．生产一件产品A的利润为2100元，生产一件产品B的利润为900元．该企业现有甲材料150kg，乙材料90kg，则在不超过600个工时的条件下，生产产品A、产品B的利润之和的最大值为元．

解析：该试题给出一些文字阅读材料，学生要能够通过阅读提取相关信息，建立数据间的关系，并且懂得利用数形结合的方法直观看出利润最大值的情况．主要考查不等式、线性规划、最值．设生产A产品x件，生产B产品y件，利润之和为z，由相关数据，可建立关系式：1.5x+0.5y=150，x+0.3y=90，5x+3y=600(x≥0,y≥0)，在直角坐标系中画出满足关系式的区域图，即可找到目标函数z=2100x+900y当x=60，y=100的时候取得最大值216000，从而得到生产产品A、产品B的利润之和最大值为216000元.

②数学文化背景

关于数学文化背景试题，虽然它具有数学阅读理解背景的特点，但由于这类试题是近年高考的热点题型，特别是自教育部考试中心《关于2017年普通高考考试大纲修订内容的通知》([2016]179号)指出：“高考在能力要求内涵方面增加数学文化的要求”之后，数学文化更是引起教育界的广泛关注，渗透数学文化的高考试题是新时期高考数学考试改革的热点，因此我们单独作为一种试题背景加以分析.

数学文化体现了数学的人文价值和科学价值，一个人的成长应该是才、学、识三者兼顾．我们往往只强调知识和能力的“学”与“才”，忽视了“识”，即见识．其实，见识是将知识和能力引向何方的根本性问题，是知识、能力形成后的个人见解，其背后的支撑是世界观、人生观、价值观．数学文化在这方面可以起到有效作用．[10]从2003年开始，无论是高考自主命题的地方卷还是全国卷，高考数学试题从数学史、数学精神、数学应用三个方面陆续渗透数学文化[16]，比如2003年高考全国卷理科第15题、文科第16题，就以著名的“四色定理”为题材进行数学文化的渗透考查．众观近年高考数学文化试题，主要涉及名著和数学名题，[17]数学文化试题的呈现有些是以“本来面目”或取其特例；有些是稍作雕琢，以简化形式呈现，但保留原有思路和方法；有些是加以拓展和推广．[18]

数学文化背景试题，在考查数学的同时也考查学生的阅读理解能力．然而，学生对数学文化试题的心声值得我们给予关注，我们曾对1007名高中生进行调查：你喜欢这种具有数学文化背景的试题吗？为什么？调查结果回答“不喜欢”的有605人，占60.08%，回答“喜欢”的有302人，占29.99%，回答“还行”的有100人，占9.93%．学生回答“喜欢”的原因大致为：“这种试题蕴含着丰富的文化背景，可以了解数学的发展史，拓展视野，领略先人们的智慧，让枯燥的数学有了文化背景，在紧张的学习之余提供了文化环境熏陶，不知不觉提高了文化自信，增加了对数学的兴趣，提高文化素养．”回答“不喜欢”的原因大致为：“这样的试题题目太长，需要大量的文字理解，很难看懂题目，考试时间紧迫，浪费读题时间，表面上极具新意，但无意中加重了考生的阅读负担，繁琐的阅读材料很容易让学生抓不到入手点，找不到关键信息，干扰学生数学思维，给对深奥文字不易理解的同学带来困难，失去了数学的意义，难以起到提升数学文化涵养的作用．”有六成的学生不喜欢这种具有数学文化背景的试题，这值得我们深思！也警示我们，要重视对学生数学阅读理解能力的培养；要创新数学文化试题的呈现方式；要将数学文化有效的渗透在常态的教学中，真正揭示数学文化的内涵，提高学生的数学文化素养；要注意数学文化试题科学、严谨的表述，不要让“阅读”成为学生高考的“拦路虎”(如例5).

例5【2017年高三质检福建卷·理4】

朱世杰是历史上最伟大的数学家之一，他所著的《四元宝鉴》卷中“如像招数”五问有如下问题：“今有官司差夫一千八百六十四人筑堤．只云初日差六十四人，次日转多七人．每人日支米三升，共支米四百三石九斗二升，问筑堤几日”．其大意为：“官府陆续派遣1864人前往修筑堤坝．第一天派出64人，从第二天开始，每天派出的人数比前一天多7人，修筑堤坝的每人每天分发大米3升，共发出大米40392升，问修筑堤坝多少天．在这个问题中，第5天应发大米

(A) 894升 (B)1170升

(C)1275升 (D)1467升

3.3 试题性质的演变

(1)封闭性试题

封闭性试题一般是指试题所给条件完备、过程确定、结论唯一，建国以来的高考数学试题，甚至从民国时期的高考数学试题，都是以封闭性为主旋律，这类试题比较普遍，我们这里就不展开分析.

(2)开放性试题

高考数学命题坚持稳中求变，变中求新，从1999年开始陆续出现一些考查探究能力的开放性试题，有条件开放、解题策略开放、结论开放和综合性开放等类型．开放题(Open Ended Problem)原是1971年日本学者岛田茂为首的一个小组的研究课题的副产品，起初只是作为检测学生数学学习水平的一种手段．在我国开始介绍开放题当始于1980年日本学者泽田利夫的一篇文章《从“未完结问题”提出的算术、数学课的教学的方案》刊登在《外国教育》第4期的时候[19]，这里的“未完结问题”就是指开放题．我国对数学开放题的集中研究当属浙江教育学院的戴再平教授，戴教授编著了5本从小学到高中的开放题集，在全国广为流传，开放题的理念迅速在全国扩展，高考数学试题中也陆续出现开放题，如1999年全国卷文科、理科第18题，2000年全国卷文科、理科第16题，之后开放性试题成为高考试题改革的一个关注点.

例6【2002年高考全国卷·文22】

(Ⅰ)给出两块相同的正三角形纸片(如图1，图2)，要求用其中一块剪拼成一个三棱锥模型，另一块剪拼成一个正三棱柱模型，使它们的全面积都与原三角形的面积相等，请设计一种剪拼方法，分别用虚线标示在图1、图2中，并作简要说明；

(Ⅱ)试比较你剪拼的正三棱锥与正三棱柱的体积的大小；

(Ⅲ)(本小题为附加题，如果解答正确，加4分，但全卷总分不超过150分)如果给出的是一块任意三角形的纸片(如图3)，要求剪拼成一个直三棱柱，使它的全面积与给出的三角形的面积相等．请设计一种剪拼方法，用虚线标示在图3中，并作简要说明.

图1

图2

图3

评析：这是一道典型的开放性试题．戴再平教授利用19世纪初波尔约——盖尔文(Bolyai-Gerwien)定理说明该题的三个小题的解法和结论有无穷多个．戴教授指出：开放性试题有利于考查学生的探究能力，特别是对创新能力的考核，而第(Ⅲ)小题采用加分的方法，这在高考评分中是一大创新．[20]对于开放性试题的评分应该采用“满意原则”、“加分原则”，只要学生给出满足问题要求的答案，就应该满意而给满分，对于解答超过一种甚至说明有无穷多种的，应该加分鼓励．如何命制更能考查学生创新意识和思维过程的开放性试题，还需要我们不断地探索与实践.

4 未来高考数学试题命制与考试时间展望

4.1 “素养立意”命题

建国以来，高考数学试题的命制经历了“知识立意”到“能力立意”的过程，《普通高中数学课程标准(征求意见稿)》[12]提出新的命题理念：要基于数学核心素养的考试命题．这也就意味着高考数学命题将向“素养立意”演进．“双基”是我国的优良传统，高考命题在保持传统精华的基础上，应该与时俱进，不断创新，在考查知识技能的同时，关注学生基本思想和基本活动经验的形成，有效考查学生发现和提出问题、分析和解决问题的能力，注重对学生核心素养达成水平的评价．以“素养立意”为导向命制试题，处理好数学核心素养与知识技能的关系，充分发挥考试对教学的积极导向作用，为人才培养，人才选拔作出贡献.

4.2 题型、题量与考试时间

建国以来，高考数学考试题量在8～28题之间摆动，2000年以来基本隐定在22题．对于高考数学考试时长，我们搜索了自1952年全国高等学校实行统一命题考试以来的高考准考证，统计发现：除1952年高考数学时长为1小时40分钟，从1953年至今，一般为2个小时，只有1977年省市自主命题时部分省(如湖北、广东)高考数学考试时长达到2个半小时．不同题型与题量却要求在相同长度的时间内作答，这一问题也许值得我们进一步思考.

2个小时的考试时间，大部分考生和老师都反映做不完．2010年张奠宙先生就“呼吁延长高考数学考试时间”，他指出：考试是检测学生解题的能力，而不是解题快慢，学生会解就行，速度并没那么重要．[21]未来高考数学要适度调整考试时间和题量[12]，也就是在不增加题量的前提下延长考试时间，给学生足够的思维时间；或在不延长考试时间的情况下，充分发挥各类试题的考查优势，科学地进行题型和题量的调整，逐步减少选择题、填空题的题量；命制一定数量的应用问题，问题情境的设计真实，来源于现实世界；以“素养立意命题”，命制更能考查学生创新意识和思维过程的开放题，以满意原则和加分原则进行评分，评分的原则和标准是思维和结果的一致性程度，如果学生的思维和结果一致，就应该满意给满分，如果学生的思维分析更深刻，就应该加分．