实际应用背景下向量法探析三角函数问题
刘淑贞 曾大恒
(湖南安全技术职业学院基础课部数理教研室 410151)
1 问题“I1sin(ωt+θ1)+I2sin(ωt+θ2) =?”的提出
以往教材中“函数y=Asin(ωx+φ)”的研究主要是“图像变换”,即参数A,ω,φ对函数图像的影响.由此,教师在教学中就把注意力集中放在三角函数图像的平移和伸缩上,让学生形式化地记住“左加右减,上加下减”,再进行大量解题操练,而对这个函数的实际意义却不加关注,结果是偏离了这一教学内容的主题,学习效果不好而且负担很重.[1]很多学生记住了大量的三角公式,能进行单纯的三角函数的计算,但却不能从内涵上去理解三角函数,在实际问题中运用三角函数.
我们在进行三角函数教学时就遇到这样一个思考题“已知有三角函数y1=I1sin(ωt+θ1),y2=I2sin(ωt+θ2)请问y=y1+y2的周期、初相位、幅值有哪些变化?”这个问题难倒了很多的同学,从教学的反馈来看,其主要原因是,一方面很多同学思考的角度是从两个三角函数的图形出发,因此面对叠加之后是怎样的图形无从下手,也就无法分析相加之后幅值、周期及相位发生了什么改变;另一方面有些同学习惯用三角公式进行推演,但由于参数较多,并且运用三角公式展开之后式子较复杂,很难整合,因此未能解决问题.下面我们首先分析一下如何从三角函数本身代数运算出发解决该问题.
2 运用三角函数公式并构建三角函数进行逻辑演绎
首先运用正弦函数的两角和公式“sin(A+B) = sinAcosB+cosAsinB”展开进行直接计算,大部分同学能做到下面一步:
由y=y1+y2=I1sin(ωt+θ1)+I2sin(ωt+θ2)
=I1(sinωtcosθ1+cosωtsinθ1)+
I2(sinωtcosθ2+cosωtsinθ2)
=sinωt(I1cosθ1+I2cosθ2)+
cosωt(I1sinθ1+I2sinθ2).
关键点及难点在于以下(1)式和(2)式的三角函数构建,需要在老师引导下少部分学生可以做到:
设I1cosθ1+I2cosθ2=Imcosθ
(1)
I1sinθ1+I2sinθ2=Imsinθ
(2)
则y=y1+y2=sinωt·Imcosθ+cosωt·Imsinθ=Im·sinωtcosθ+Im·cosωtsinθ=Imsin(ωt+θ),
其中Im和θ的取值可由前面的构建的三角函数(1)和(2)式左右两边分别平方相加解出:
(I1cosθ1+I2cosθ2)2+(I1sinθ1+I2sinθ2)2

(3)
同时将(1)式比(2)式得

(4)
最终得出结论
y=y1+y2=I1sin(ωt+θ1)+I2sin(ωt+θ2)
=Imsin(ωt+θ),
可知两个同周期的三角函数相加后周期不发生改变,并且由(3)、(4)知新的幅值
以上的这种运用三角公式、构造三角函数来进行逻辑演绎是解决三角函数有关问题的常用方法,通常情况下都会想到用这种方法直接对这两个三角函数相加,然后来分析y1+y2的周期、初相位、幅值情况,但是假设构建“I1cosθ1+I2cosθ2=Imcosθ(1),I1sinθ1+I2sinθ2=Imsinθ(2) ”这两个式子很难从代数角度想得到.
同时,用公式进行逻辑演绎严谨抽象,思维缺少一个具体直观的载体,学生很难将思想集中起来,对问题本身的理解和应用都不是很深刻,如若借助一些实际背景、直观形象的处理方法,则可收到较好的效果.
3 电学背景中与数学中的三角函数y=Imsin(ωt+θ)的关联
从函数的本质看,应强调三角函数作为描述周期现象的重要数学模型的地位,因为“三角函数与其它学科的联系与结合非常重要,最重要的是它与振动和波动的联系,可以说,它几乎是全部高科技的基础之一”.[2]
比如生活中最简单常用的交流电,其电流与电压等物理量的大小和方向会随时间按正弦函数的规律发生周期性的变化.因此,生活及电力工程中所用的电流与电压,通常都采用正弦函数的形式来进行电路电波的分析.[3]正弦交流电中,电流强度i随时间t变化的规律可以用函数表示为i=Imsin(ωt+θ),(Im>0,ω>0,-π≤θ≤π),其中Im是电流强度的最大值,称为幅值(或峰值);ω称为角频率,表示电流变化的快慢;θ称为初相位,ωt+θ称为相位,相位可以表示电流强度在某时刻的大小和方向.正弦交流电的幅值、频率、初相位三要素对应正弦三角函数的最值、周期、角度初值三个函数特征.如下表一:

表一 y=Imsin(ωt+θ)各指标在数学与电学中对应
4 电学背景下三角函数y=Imsin(ωt+θ)的向量表示
正弦交流电产生原理是:闭合线圈在匀强磁场中绕垂直于磁场的轴匀速转动时,线圈里就产生大小和方向作周期性改变的正弦交流电.依据这样的一个原理,我们可以在数学上用旋转向量来对应正弦波函数y=Imsin(ωt+θ),具体如下图1.

图1
5 向量法求解问题“I1sin(ωt+θ1)+I2sin(ωt+θ2)=?”
问题“I1sin(ωt+θ1)+I2sin(ωt+θ2)=?”在生活中是指两个同频率的正弦交流电相叠加之后,角频率、幅值和相位会有哪些变化?前面我们知道,可以用模为Im,初始角度为θ,角频率ω的旋转向量在纵轴上的投影来对应一个形式为y=Imsin(ωt+θ)的正弦函数量.因此我们可以通过两个对应的向量相加来解决.
BIM技术的应用实现了对整个施工过程的空间、时间和资源的动态统一管理,提高了施工生产效率,降低了能耗,有效促进了绿色施工。施工场地基坑平面布置如图2所示。
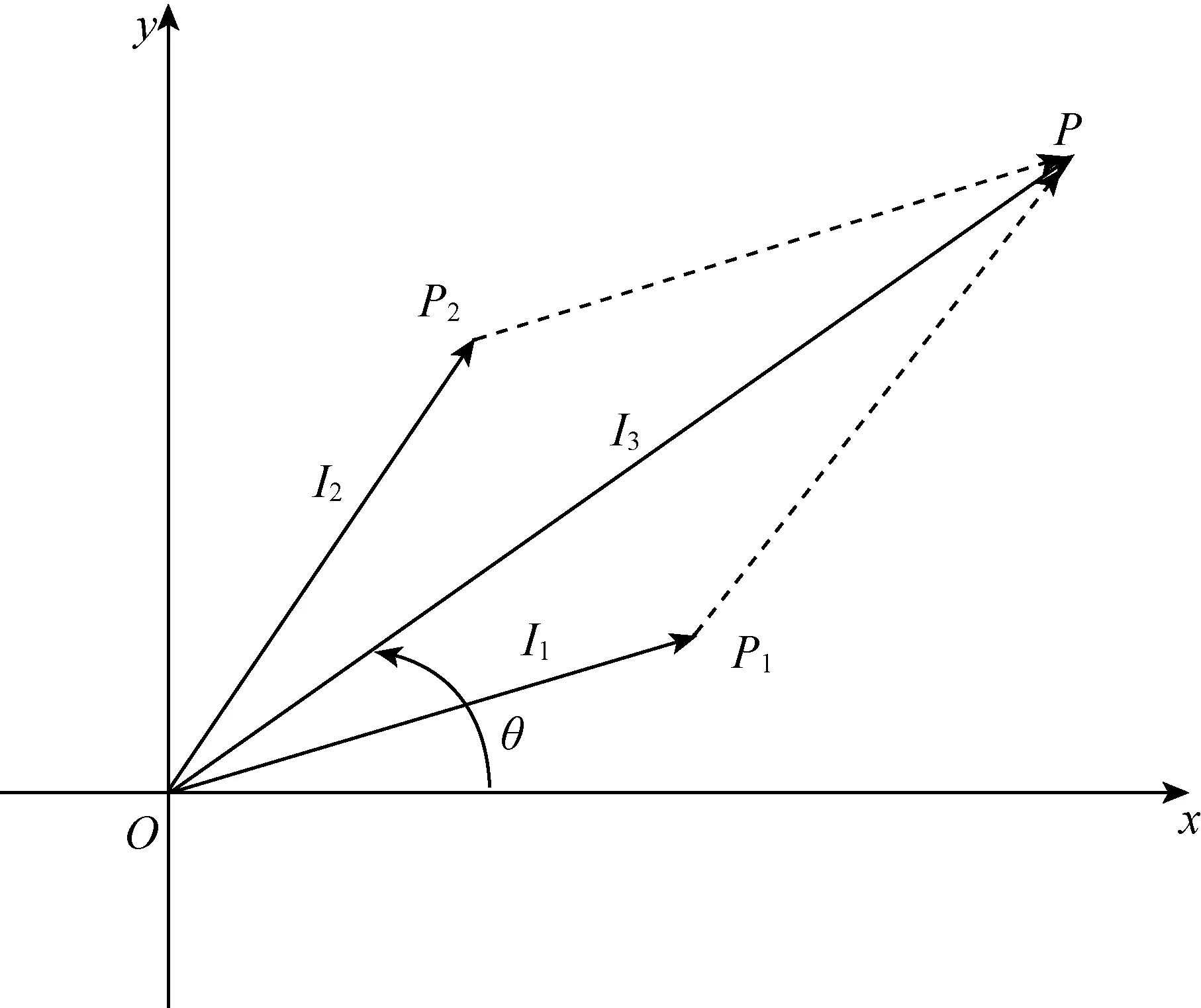
图2


图3


也可以在△OPP2中利用余弦定理同样可得到

因此可得到I1sin(ωt+θ1)+I2sin(ωt+θ2)的最大幅值


这种在实际电路背景下,借助向量加法在几何上的意义,以及向量与三角函数的映射可以直观具体地让学生理解两个正弦向量的叠加的深度含义,对数学的应用意识的培养有积极的作用.
6 总结
弗莱登塔尔在他的“数学现实”教学原则中就提出,数学来源于现实,也必须扎根于现实,并且应用于现实.他强调数学教育要引导学生了解周围的世界,周围的世界是学生探索的源泉.[5]思考和解决数学问题如若借助恰当的生活实际背景去处理比单从数学逻辑出发会理解的更深入、更具体、更能培养数学的应用意识,从而让学生能直观地体会到数学的价值感.有许多人正是通过一种“非正规”的方法来接受来理解数学的概念、数学的公式、数学的思想方法,从而爱上数学.不得不说以上的向量法解决三角函数问题放弃了逻辑的严格性,但却更生动形象并具有创造性思维.因此,数学教学中应该严谨的逻辑演绎与直观形象的几何解释相并存,从数学本身出发与从生活实际出发思考问题相辅助,才能让学习者更深刻的、更丰富的、更全面的理解并掌握数学.

