正方体模型的开发和利用

周顺钿

(浙江省杭州高级中学 310003)

2016年以来，“核心素养”成为教育界关注的一个焦点.在“基本运算、逻辑思维、空间想象”的“老”三大能力和“数学抽象、数学建模、数据分析”的“新”三大能力的基础上，提出了数学核心素养的六个要素：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.章建跃先生指出：为培养和发展学生的数学核心素养，需要我们扎实开展数学教育的实践研究，搞出一批“核心素养统领下的数学教学案例”，使抽象的“核心素养”获得具体事例的支撑[1].

“数学建模”包含模型建立和模型应用两大方面，是数学核心素养之一.单墫先生说：“模式教育容易产生定势思维，束缚创造性，但完全没有模式，也使初学者难以把握，正如围棋中的定式，需要根据情况灵活应用、不可拘泥.”[2]正方体就是一个极具价值的空间模型，掌握正方体的结构特征，以正方体为模型可以“生成”许多优美的空间问题，许多空间问题如果将它置于正方体模型之中，其结果甚至可以一望而解.

1 正方体模型的价值分析

1．正方体是空间图形中最特殊且内涵最丰富的几何图形，它享有“万能模型”的美称.正方体作为立体几何教学的一个关键突破口，是因为它具有如下四个特征.

(1)正方体是学生最早接触和最熟悉的空间图形，具有很强的空间感.借用它进行立体几何教学，有利于学生建立空间概念、克服畏难情绪，有助于学生观察点、线、面位置，降低思维难度.

(2)正方体能完美体现立体几何核心知识.正方体包含了众多的空间中基本的线线关系、线面关系、面面关系，基于正方体模型，即可把立体几何中的基本概念与基本定理梳理清楚.

(3)对正方体进行切截、割补，可以得到多种多样的柱体、台体、锥体等，既可以拓展、丰富立体几何的研究空间，又体现出图形与知识间的内在联系.

(4)正方体是探索解题思路的重要突破口.很多立体几何问题由于线面关系复杂或图形不容易画出，容易导致思路阻塞，借助正方体模型，可以把研究对象置于更大的背景之中，从而在整体上更好地看清各部分之间的关系.

2. 正方体包含了众多的点、线、面及其相互关系，剖析正方体，有助于学生理解正方体，并高度重视正方体的作用.

(1)棱长为a的正方体有以下常见特征

(i)正方体有6个面、8个顶点、12条棱，满足面数+顶点数-棱数=2(欧拉定理)；

(ii)正方体的12条棱可以组成24对异面直线；

(iii)正方体有13条对称轴、9个对称面；

(iv)由正方体的顶点组成的三角形中，锐角三角形8个，直角三角形48个；

(v)正方体绕其对角线旋转120°后，与原正方体位置重合；

(vii)一个平面截正方体，其截面可以是：三角形、正方形、菱形、矩形、梯形、平行四边形、五边形、六边形.

(2)正方体中具有特殊意义的线、面往往单独形成研究系列.例如正方体的棱、面对角线、体对角线通常简称为正方体的三类线，正方体的底面、对角面、与同一顶点相邻的三个顶点构成的截面，通常简称为正方体的三类面，围绕这些线与面可以编制出一系列有趣的空间问题.

(i)求三类线两两所成角的大小；

(ii)求三类线与三类面间线面所成角的大小；

(iii)求三类面间分别组成的二面角的大小；

在学习数学的过程中，所积累的知识经验经过加工，会得出有长久保存价值或基本重要性的典型结构与重要类型――模式，将其有意识地记忆下来，并作有目的的简单编码，当遇到一个新问题时，我们辨认它属于哪一类基本模式，联想起一个已经解决的问题，以此为索引，在记忆贮存中提取出相应的方法来加以解决，这就是模式识别的解题策略[3].在教学实践中，教师可充分发挥正方体模型的价值，积极高效地引导学生进行立体几何的学习.

2 正方体模型的开发和利用

“生”和“成”是构成“生成”的两个方面.“生”是指事物从无到有的过程，含有产生、出现、创造之意；“成”为形成之“成”或成果之“成”，强调事物变化的过程和结果.“生成”指事物的出现、产生与形成过程，具有过程性、发展性和创造性的意义，它是一种既有起点又有终点的过程.教师要鼓励学生成为生成性资源的发掘者，正方体模型具有很好的开发和利用的价值.

2．1 提取

“有效提取数学信息”是指学生能够在有限的时间内从文字、图表等信息呈现方式中提取准确、必需的数学信息．正确提取数学信息的能力是学生分析与解决问题的基本途径，也是新课改理念下高中数学教学所必需关注的基本目标．正方体具有丰富的点、线、面的关系，是一个很好的信息源，从中“提取”一部分加以研究，就可以“生成”许多优质的空间问题.

2．1．1 生成概念辨析问题

立体几何中许多概念性问题，都可以从正方体中找到相应的模型.

例1(1)三棱锥的四个面最多可以有多少个直角三角形？

(2)三个内角为直角的四边形一定是矩形？

(3)一个二面角的两个面分别与另一个二面角的两个面垂直，这两个二面角的大小相等或互补？

图1 图2 图3

分析：以正方体ABCD-A′B′C′D′为模型进行有效提取.(1)如图1，三棱锥D′-ABD的四个面均为直角三角形，故三棱锥的四个面最多可以有4个直角三角形；(2)如图2，空间四边形ABB′D′有三个内角为直角，但它不是矩形；(3)如图3，二面角A′-AD-C的两个面分别与二面角D′-CC′-M的两个面垂直，这两个二面角的大小没有必然联系.

2．1．2 生成三视图的问题

三视图问题常常是由几何体提取部分后逆向编制而成的.

例2(1)(2014全国1理12题)如图4，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为( )

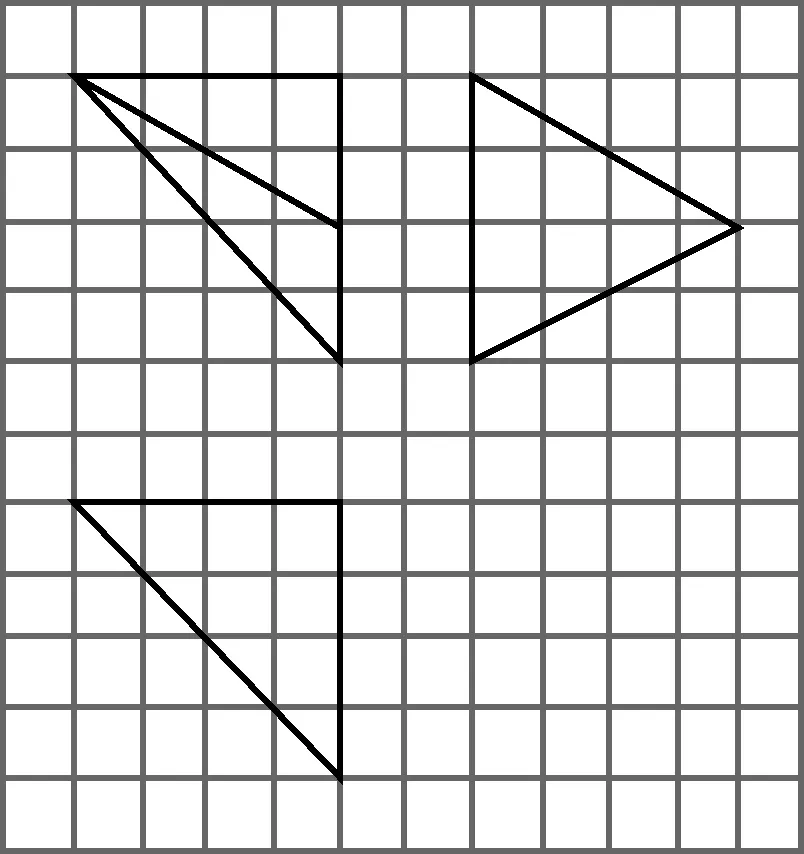
图4

图5

分析：如图5，从边长为4的正方体中提取三棱锥D-ABC，再画出三视图就“生成”了这个高考题，其最长的棱长为DA=6，选B.

(2)某几何体的三视图如图6所示，则该几何体的体积为.

图6

图7

目前，全国各地设计的三视图问题的难度都有上升趋势，实际上要设计一个这样的问题是容易的，但要学生逆向画出直观图，的确有些强人所难.

2．1．3 生成角与距离的计算问题

角与距离的计算是立体几何的核心问题，由正方体“生成”问题是一条讨巧的捷径.

例3(2016年天津理17题)如图8，正方形ABCD的中心为O，四边形OBEF为矩形，平面OBEF⊥平面ABCD，点G为AB的中点，AB=BE=2.

(1)求证：EG∥平面ADF；

(2)求二面角O-EF-C的正弦值；

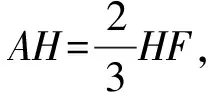
图8

图9

分析：如图9，在棱长为2的正方体中提取多面体EF-ABCD，就“生成”了2016年天津理17题，在这个正方体模型中，可轻松地解决相关问题.

(1)求证：ADBC；

(2)求二面角B-AC-D的大小的余弦值；

图10

(3)在直线AC上是否存在一点E，使ED与面BCD成30角？若存在，确定E的位置；若不存在，说明理由.

图11

分析：如图11，在单位正方体中提取三棱锥A-BCD，就“生成”了2006年江西理20题.

2．1．4 生成球的切接问题

正方体的内切球和外接球都是很好的研究对象.

例5如图12，在棱长为a的正方体ABCD-A1B1C1D1内有一个内切球，M、N分别为AB、CC1的中点，且MN与球交于E、F两点，线段EF长为( )

图12

例6(2007年复旦自主招生题)棱长为a的正方体内有两球互相外切，且两球各与正方体的三个面相切，则两球的半径之和为( )

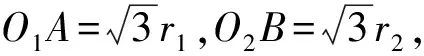
图13

2．2 嵌入

“嵌入”的字面解释是“牢固地或深深地固定或树立”，如果一个空间问题的研究对象可以置于一个正方体中，那么可以从整体上更好地看清各部分之间的内在关系.“嵌入”和“提取”是矛盾对立统一的两个方面，是相辅相成的.

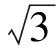
图14

评注：本题考查球与正三棱锥的切接问题，若直接利用三棱锥来考虑难度较大,注意到条件中的垂直关系,把三棱锥转化为正方体来考虑就容易多了.

例8(2009年江西理9题)如图15，正四面体ABCD的顶点A，B，C分别在两两垂直的三条射线Ox，Oy，Oz上，则在下列命题中，错误的为( )

A．O-ABC是正三棱锥

B．直线OB∥平面ACD

C．直线AD与OB所成的角是45°

D．二面角D-OB-A为45°

图16

分析：如图16，将正四面体ABCD“嵌入”正方体中，则正四面体的棱为其所在正方体的面对角线，从正方体中观察此图，易知直线OB∥平面ACD是不可能的.选B.

评注：利用正方体与正四面体之间的“蕴含”关系，借助正方体模型可轻松解决正四面体中点、线、面之间的位置关系.

例9(2006年江苏9题)两相同的正四棱锥组成如图17所示的几何体，可放在棱长为1的正方体内，使正四棱锥的底面ABCD与正方体的某一个平面平行，且各顶点均在正方体的面上，则这样的几何体体积的可能值有( )

A．1个 B．2个 C．3个 D．无穷多个

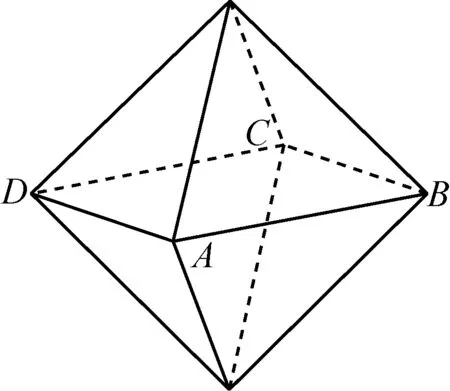
图17

图18

分析：如图18，由于两个正四棱锥相同，所以所求几何体的中心为正四棱锥底面正方形ABCD中心，由对称性知正四棱锥的高为正方体棱长的一半，影响几何体体积的只能是正四棱锥底面正方形ABCD的面积，于是问题转化为考察边长为1的正方形可以有多少个内接正方形，显然有无穷多个.选D.

评注：正方体是大家熟悉的几何体，它的一些内接或外接图形需要一定的空间想象能力，要学会将空间问题向平面问题转化.

2．3 运动

“动态”立体几何问题由于注入了某些变化的点、线、面、体等元素，常常集“知识的交汇性与综合性、方法的灵活性与多向性、思维的变通性与深刻性”于一体，使立体几何问题更富思辨性、开放性和挑战性，这与“以能力立意”的高考命题指导思想和“将知识、能力与素质的考查融为一体，全面检测考生的数学素养”的高考数学命题原则相吻合.将正方体中的某些要素“动”起来，甚至将整个正方体“动”起来，是一个很“时髦”的“生成”手段.

例10(2017年4月金华十校模考题)如图19，在正方体ABCDA1B1C1D1中，点M、N分别是直线CD、AB上的动点，点P是△A1C1D内的动点(不包括边界)，记直线D1P与MN所成角为θ，若θ的最小值为则点P的轨迹是( ).

图19

A.圆的一部分 B.椭圆的一部分

C.抛物线的一部分 D.双曲线的一部分

例11如图20，直线l⊥平面α，垂足为O，正方体ABCD-A1B1C1D1的棱长为2，点A是直线l上的动点，点B1在平面α内，则点O到CD1中点P的距离的最大值为( )

图20

图21

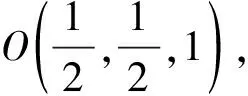
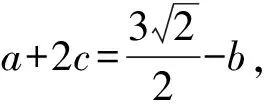
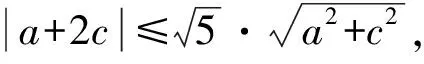
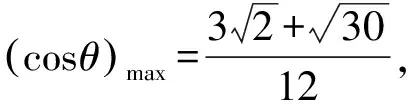
图22

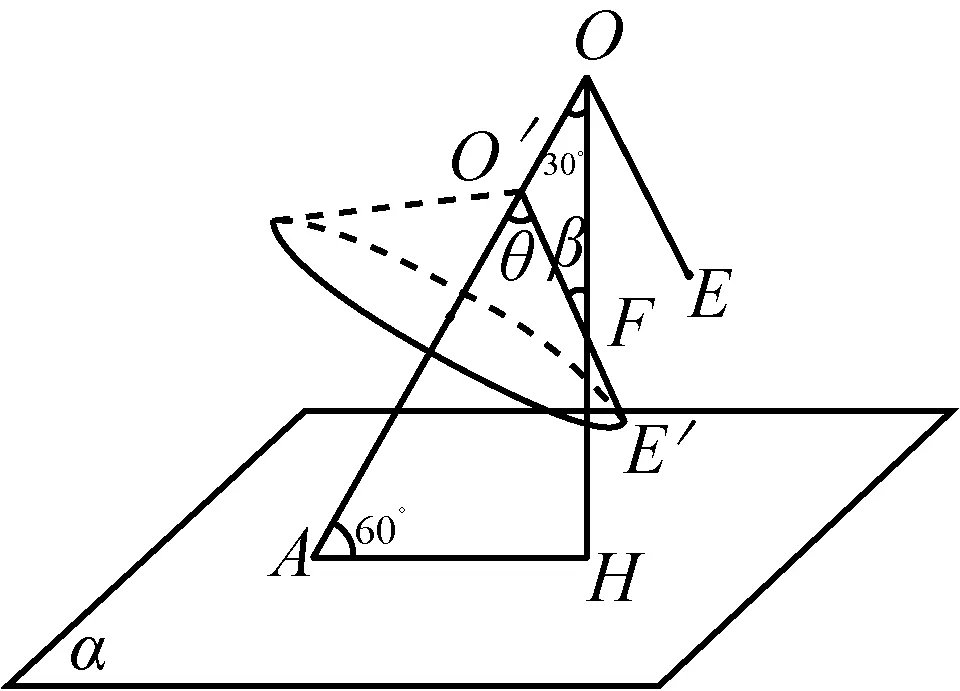
图23

如图23，为了便于观察，我们将OE下移至O′E′.当正方体ABCD-A1B1C1D1绕着OA旋转一周时，平面C1D1DC的法线OE(也即O′E′)绕着OA旋转一周时形成一个圆锥的侧面.记平面C1D1DC的法线O′E′与平面α的法线OH所成角的最小值为β，平面C1D1DC与平面α所成

教学是在资源的不断“生成”与“利用”的反复交替过程中进行的，是在学生已有经验的基础上，推动学生的认知发展和知识建构.教师作为教学信息的重组者，在开发和利用动态生成性资源时，应努力激发学生的动机、尊重学生的兴趣、把握信息的价值、推动信息的增值，实现课堂教学的动态生成.

从双基教学的产生，到素质教育、情感态度价值观、学生学科核心素养等一系列理念的提出、研究和实施，不难发现，在这个变化发展的过程中，教育教学目标的实施一步步具体、明确、可操作，充分体现了基础教育研究的不断深入，体现了教育研究水平的不断提高.布鲁纳曾经指出：“我们教师的目的在于：我们应当尽可能使学生牢固地掌握学科内容.我们还应当尽可能使学生成为自主而自动的思想家.这样的学生，当他们在正式学校教育结束之后，将会独立地向前迈进.”