高三复习不可忽视立体几何的作图问题

宋建辉

(福建省福州格致中学 350001)

本文缘起2016年全国乙卷文科第18题立体几何解答题，该题实测得分率非常低，堪称2016年文科考生的“黑色18题”，这一现象引起了笔者的关注与思考.

实际上像此类作图问题，课本中就有，如人教A版必修2第59页例3，人教A版必修2第63页B组第1题，人教A版必修2第78页A组第2题等；历年的高考试题也不少，如2016年四川理18题；2013年福建理19题；2013年福建文18题；2013年湖北理19题；2013年四川理19题，文19题；2013年安微理15题，文15题；2009年安微理18题；2002年全国高考文科22题.于是我们可以看到，这不是新的题型，但是在高三复习时，甚至在高一高二时就被忽视！原因之一是立体几何作图问题较少考到，原因之二是广大教师没有意识或认识到作图在立体几何中的教学价值和问题解决中的作用.本文主要归纳出蕴含“推理论证”型的立体几何的作图问题，以引起广大教师的关注，为高三复习带来一点启示.

1 正方体的截面

关于平面截正方体的问题，在初高中的教材均有所呈现，但多数教师在教学中基本上采用课件或几何画板演示来教学，而忽视了从作图(实际操作)角度来进行教学，导致考生在具体情境中仍无法顺利解决问题.

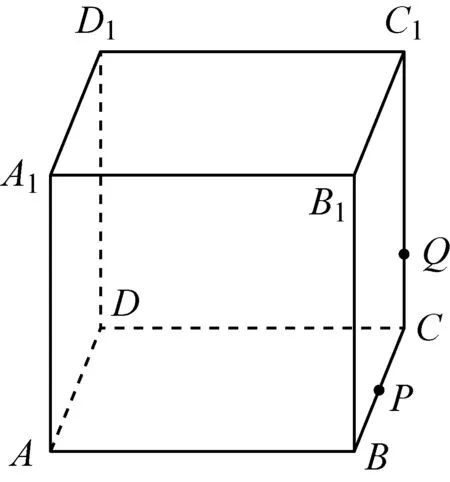
例1(2013年安徽理(文)15题)如图，正方体ABCD-A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的动点，过点A，P，Q的平面截该正方体所得的截面记为S.则下列命题正确的是________(写出所有正确命题的编号)．

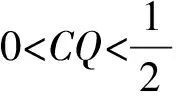
分析对该题的解答，多数都是从证明的角度逐一解决，无疑背离了该题的命题意图和考查目标，立足“作图”，从整体上给予问题的解决，方是本题考查的宗旨.

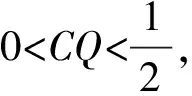
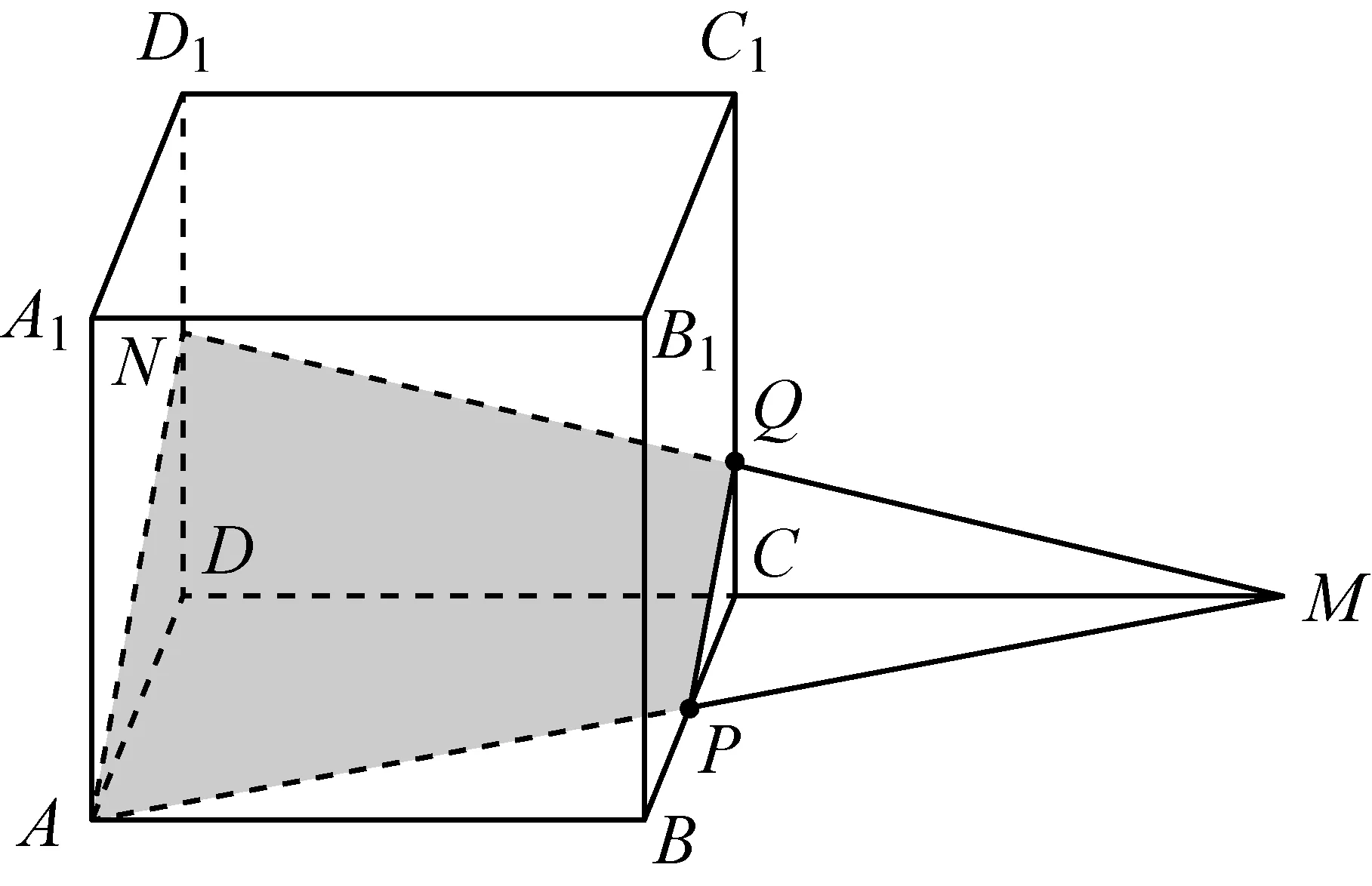
此题对考生来讲并不陌生，甚至似曾相似，但考生完成的并不理想，究其原因就是我们的教学出了问题，我们只让学生“眼观空想”，而没有让学生实践操作，真正作图.该题还可以作为公理3教学的很好的素材.

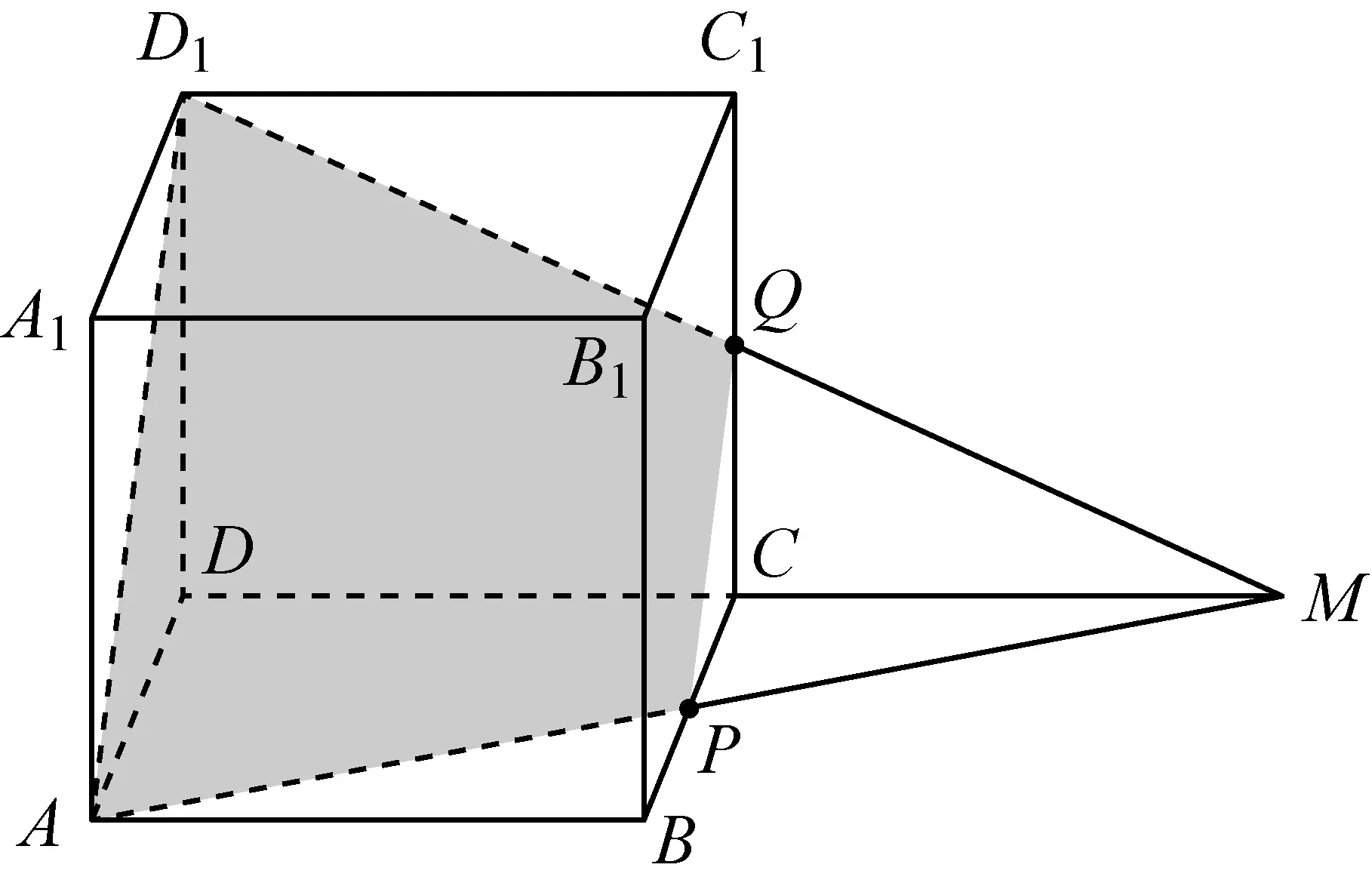
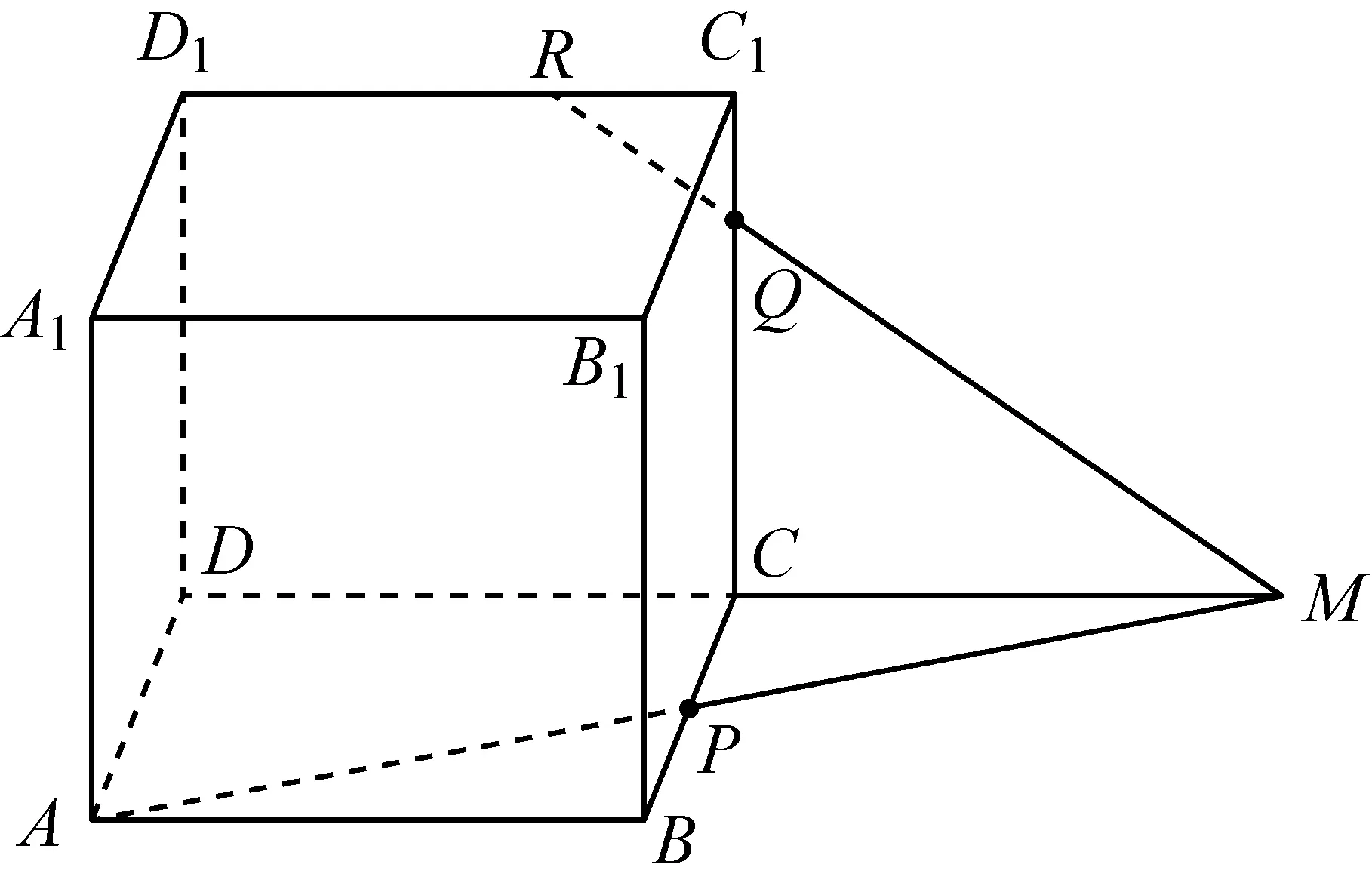
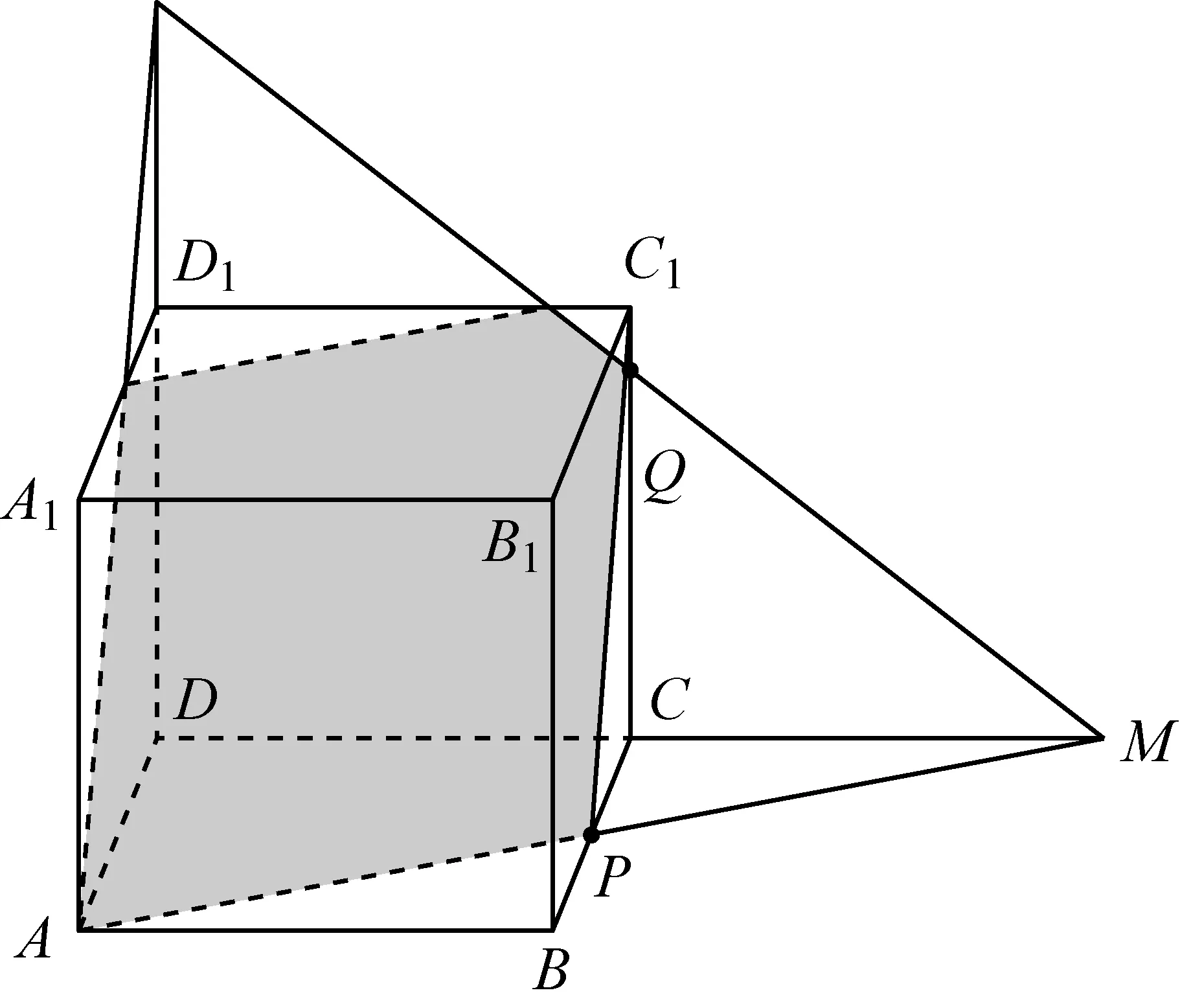
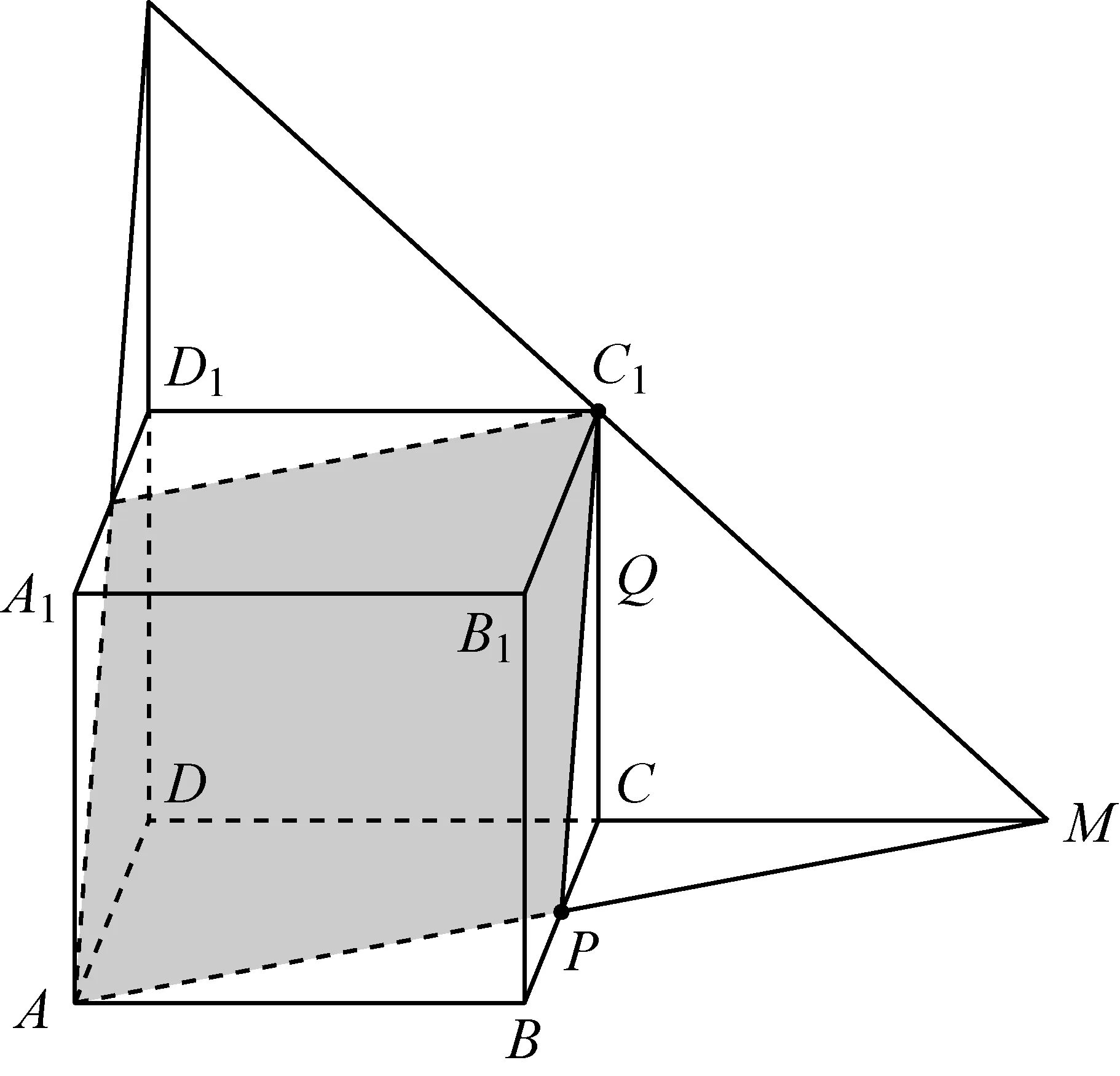
该题还可以继续拓展：用平面截正方体，①截面何时是三角形？是锐角三角形，钝角三角形，还是直角三角形？有没有可能是等腰三角形或等边三角形？②截面何时是四边形？并说明四边形的形状；③截面会是五边形？六边形吗？我们说，容易的做熟了，就没有难的了；简单的做细了，就没有复杂的了，本题的教学若能从作图的角度展开，无疑会让我们的学生再遇到截面问题就有思路可寻了.

2 平行问题

例2(2015年全国Ⅱ卷文理19题)如图，长方体ABCD-A1B1C1D1中，AB=16，BC=10，AA1=8，点E，F分别在A1B1，C1D1上，A1E=D1F=4．过点E，F的平面α,与此长方体的面相交，交线围成一个正方形．

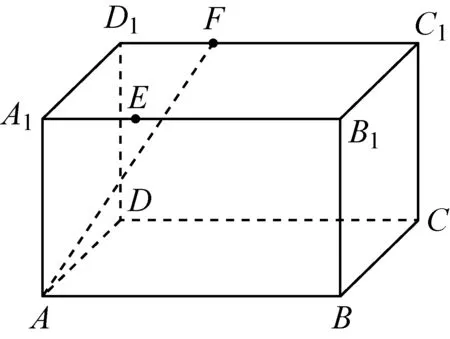
(Ⅰ)在图中画出这个正方形(不必说明画法和理由)；(Ⅱ)略.

分析这道题当时特别受到大家的好评，一方面是考到了很多年没有考到的作图问题，能够引导大家真正去重视基础；另一方面，也是因为命题专家认为这道题考查了学生的实践能力.这道题来源于哪里呢？源于课本，源于人教A版必修2第59页例3的改编.本题解答要求是不必说明画法和理由，因此完成它还是比较容易的.

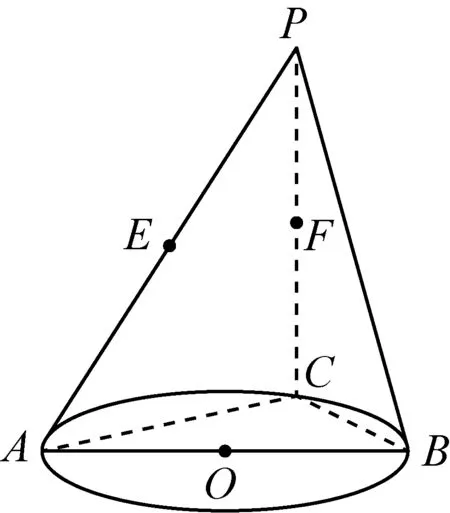
例3(2013年湖北理科19题改编)如图，AB是圆O的直径，点C是圆O上异于A,B的点，直线PC⊥平面ABC，E,F分别是PA,PC的中点.

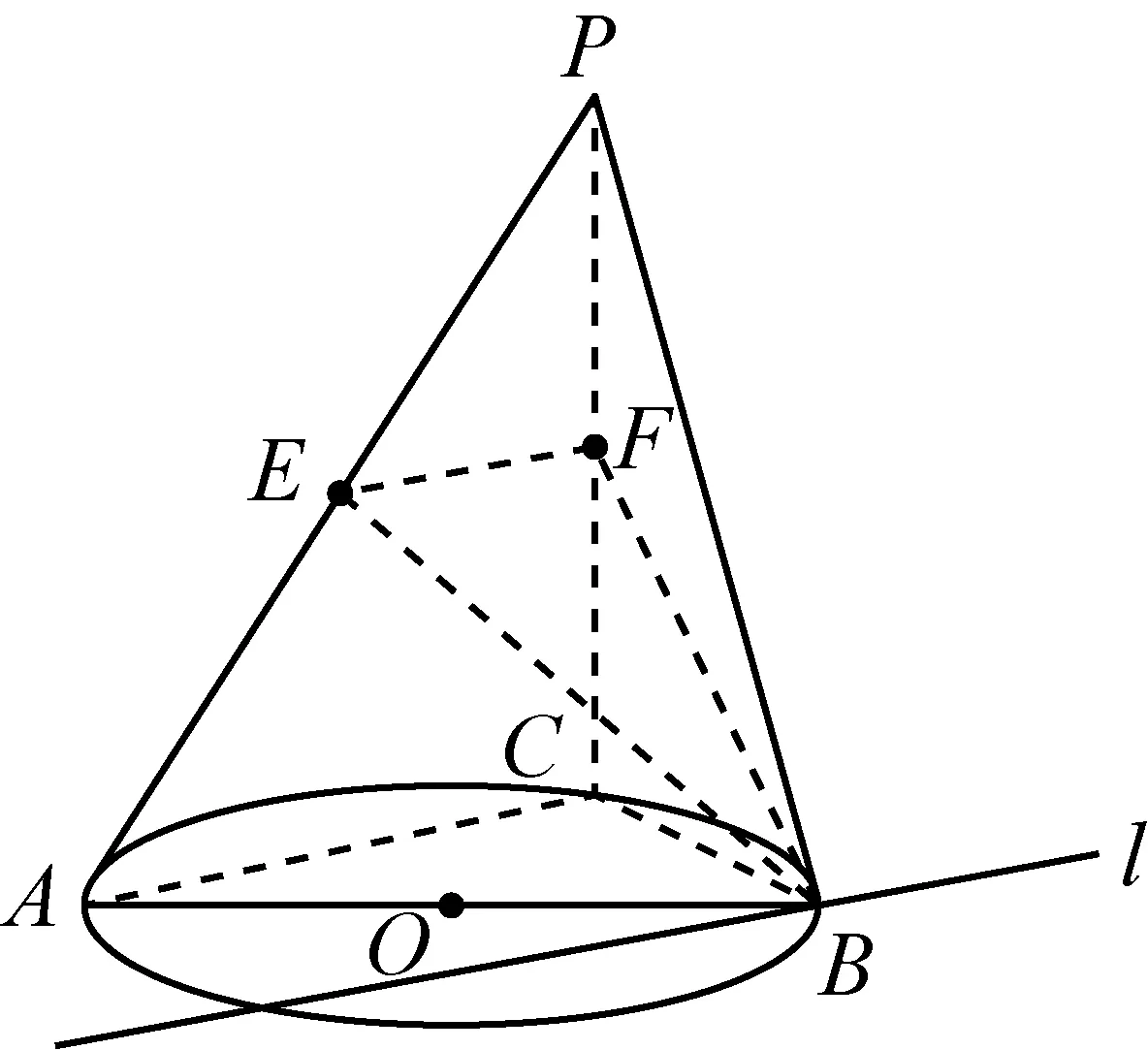
(Ⅰ)请你画出平面BEF与平面ABC的交线l，并说明画法和理由；(Ⅱ)略.

分析本题显然比例2略难一点，因为图中只出现了平面BEF与平面ABC的一个公共点B，要画出交线，则需确定另外一个公共点，那如何画呢？此时需要考生从理性到感性，从证明回归作图，是对空间想象能力完美的考查.

解析连接EF，因为E,F分别是PA,PC的中点，所以EF∥AC，从而易证EF∥平面ABC，而EF⊂平面BEF，且平面BEF∩平面ABC=l，所以EF∥l，从而AC∥l，故在平面PAC上，过点B作直线l∥AC，l即为所作的平面BEF与平面ABC的交线.

立体几何中的平行作图，不同于平面几何，它需要考生对直线与平面平行的性质与判定定理、平面与平面平行的垂直与判定定理的深刻理解，以及较强的空间想象能力.

3 垂直问题

实际上垂直问题比平行问题更难，因为在直观图中垂直关系基本上不能依赖直观观察，它的解决需要学生更强的空间想象能力，推理论证能力和更熟练完备的知识体系.人教A版必修2第78页A组第2题就是一个垂直的作图问题，在实践中学生就完成不好，下面且看2016年全国乙卷文科第18题分析.

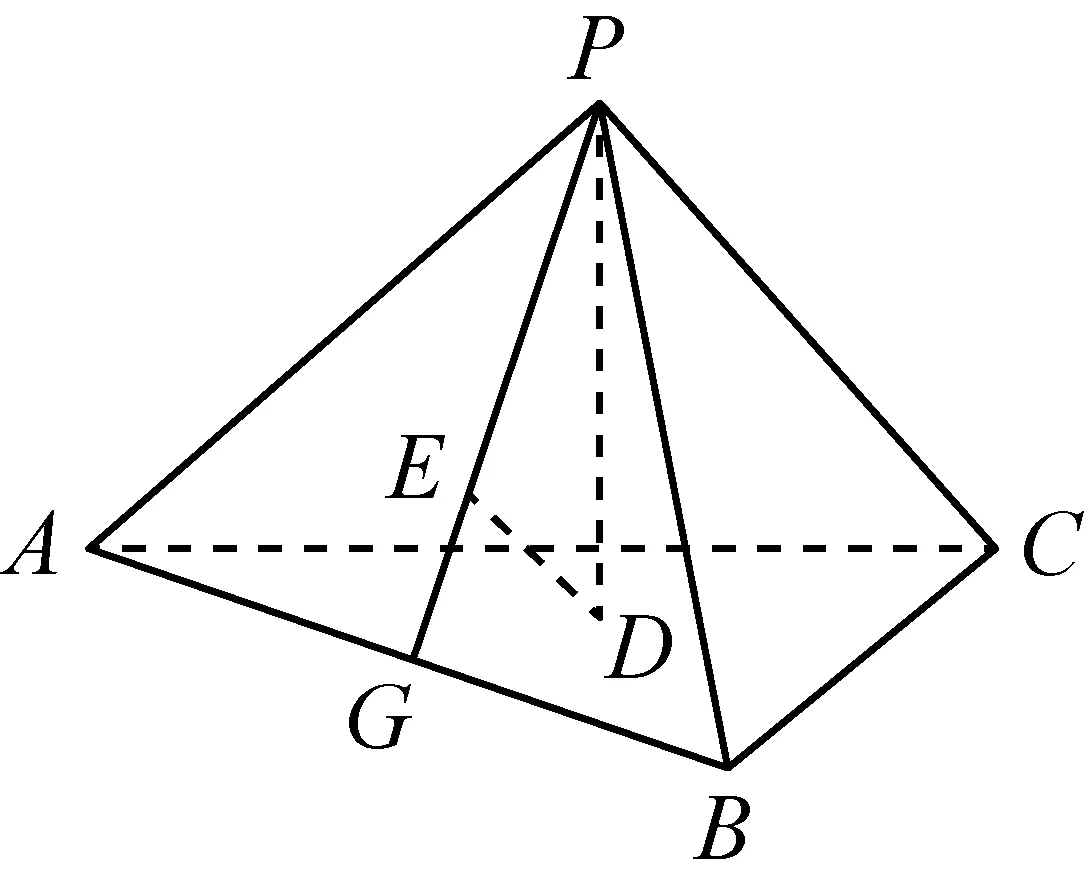
例4(2016年全国乙卷文科第18题)如图，已知正三棱锥P-ABC的侧面是直角三角形，PA=6，顶点P在平面ABC内的正投影为点D，点D在平面PAB内的正投影为点E，连接PE并延长交AB于点G.

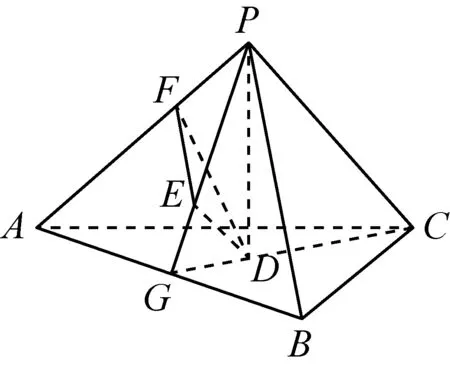
(Ⅰ)略；(Ⅱ)在答题卡第(18)题图中作出点E在平面PAC内的正投影F(说明作法及理由)，并求四面体PDEF的体积．

解法1在平面PAB内，过点E作PB的平行线交PA于点F，F即为E在平面PAC内的正投影.

理由如下：由已知可得PB⊥PA，PB⊥PC，又EF∥PB，所以EF⊥PC，因此EF⊥PA，EF⊥PC，又PA∩PC=P，所以EF⊥平面PAC，即点F为E在平面PAC内的正投影.(求体积略)

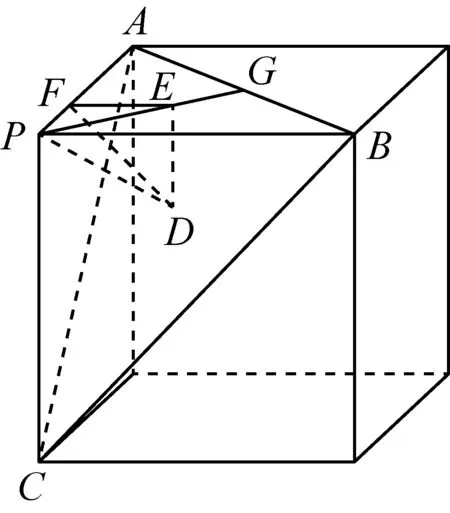
解法2若注意到该题的正三棱锥的侧面是直角三角形，与正方体这个典型的几何体相联系，将该问题放置在正方体中研究则显得更为直观、易证.

如图，正方体中P-ABC显然是满足条件的三棱锥，过点E作EF⊥PA于F，在正方体中，平面PAB⊥平面PAC，且平面PAB∩平面PAC=PA，所以EF⊥平面PAC，即F为E在平面PAC内的正投影.

笔者曾将该题给理科生做，同样也完成得非常不理想，这是我们教学中长期忽略作图问题的后果，应引起广大教师的关注，同时应思考我们立体几何教学的问题所在.

4 翻折拼接问题

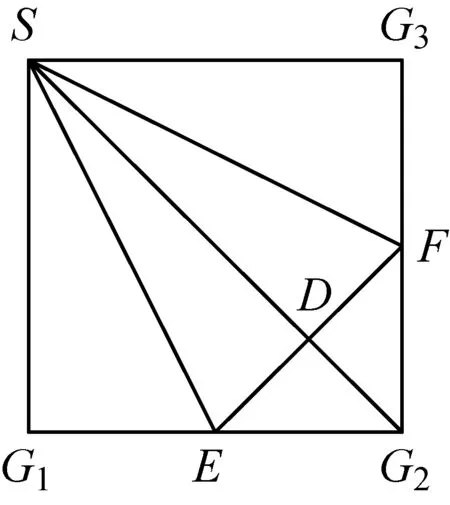
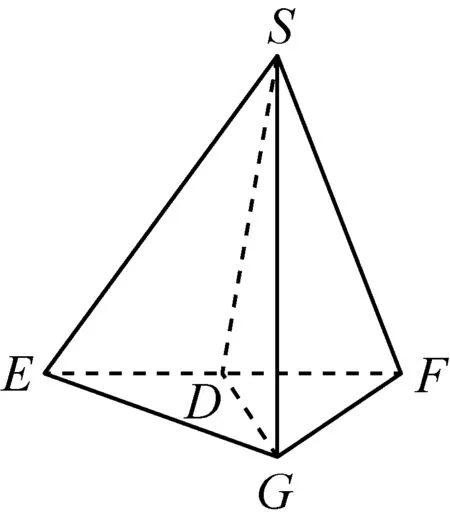
例5(人教A版第73页练习改编)如图，正方形SG1G2G3中，E,F分别是G1G2，G2G3的中点，D是EF的中点，现在沿SE,SF及EF把这个正方形折成一个四面体，使G1,G2,G3三点重合，重合后的点记为G.

(1)画出翻折后几何体的直观图；(2)求证：平面GEF⊥平面GDS.

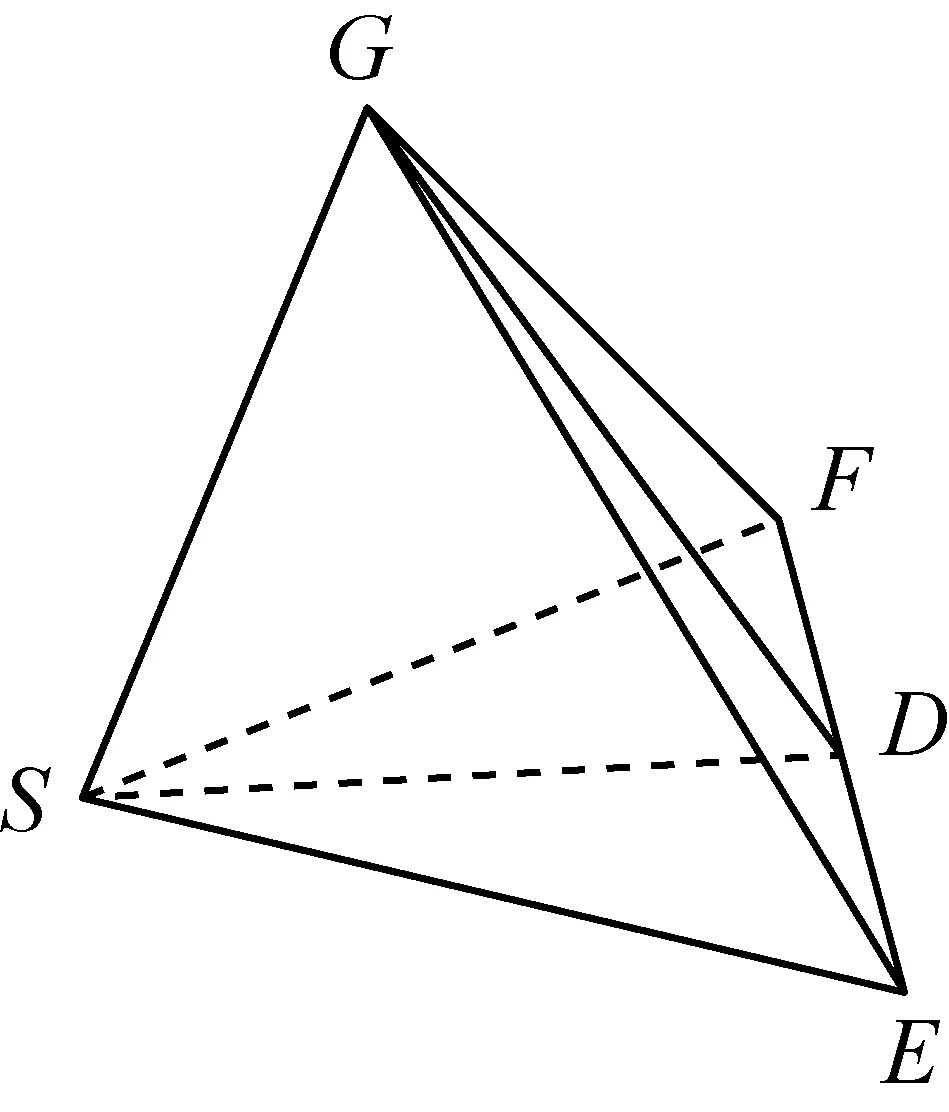
分析本题源于一节听课后的思考.授课教师在上课时，将该题改编为证明平面GEF⊥平面GDS，并给出了翻折后的图形(如右图). 对于这道题来说，最难的一点就是，学生怎样画这个立体图，怎么画这个立体图，老师给画出来了，让学生去证，怎么可能证不出来呢？老师给了图，就背离这道题的命制意图，它的价值也就大打折扣了.讲这道题最理想的方法是，就是让学生画图，画图的过程实质就是证明过程，画完图，这题也就证明完了.如此，该图形有以下三种画法，均体现了对这个翻折前后几何关系的深刻理解和把握.

因此该题应作如下改编.

问题1：动手操作：请同学们拿出一张A4纸裁成正方形，根据题目的要求，折出这个四面体.

问题2：根据你折成的四面体，画出四面体S-EFG的直观图.

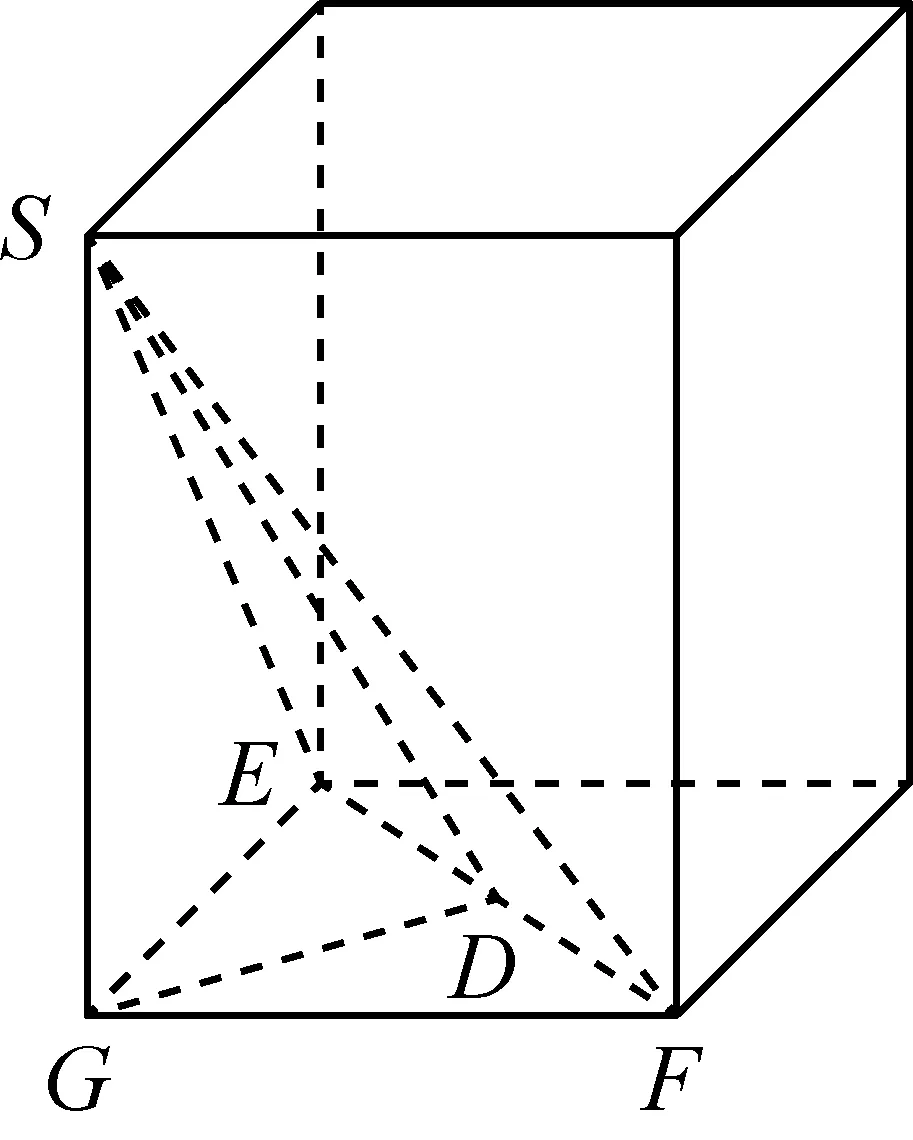
问题3：请你判断平面GEF垂直于平面GDS吗？若垂直，请证明；若不垂直，请说明理由.

问题4：你还能提出哪些问题？(预期：求四面体S-EFG外接球的体积；求点G到平面SEF

的距离；求证：点G在平面SEF的正投影是△SEF的垂心；如果点D是EF上的任意一点，平面GEF⊥平面GDS吗？……)

以翻折为背景命制的立体几何试题，随处可见，但基本上都是给出了翻折后的几何体的直观图，如果让学生画出直观图，无疑会加大试题的难度，从更高层面上考查学生的空间想象能力.至于裁剪拼接问题，在这里就不一一赘述了，读者可以关注2002年全国高考文科22题和2013年福建高考理科第19题.

以上这类蕴含“推理论证”的立体几何作图试题，让我们看到了与传统立体几何解答题不同的、别具一格的崭新面貌，问题的解决需要学生综合运用立体几何知识，对能力要求较高.因此，在高三复习阶段，尤其在日常教学中，我们要认识到作图问题是立体几何中最基础、最基本的知识，是学习立体几何最重要的基本功，更要重视蕴含“推理论证”的立体几何作图问题的研究，切忌遇到作图问题只用课件或几何画板让学生“眼观空想”，应切实让学生动手画图，引导学生理性作图，我们有理由相信，通过这些作图问题可以大大提高学生的空间想象力和推理论证能力，领悟学习立体几何的核心所在，拓展学生理性思维的广度和深度.