数学教学 不要丢掉根本

吴 彤

(江苏省盐城市教育局教科院 224000)

1 不正常现象

日常教学中，经常出现一些“怪”现象，令我们教师费解.如教师认为很简单的题，学生却发生了高错误率；教师认为很好理解的问题，很多学生却想不通等等.最近，笔者在高三一轮复习中，碰到了两个不正常现象，印象非常深刻.

现象之一：一些重要的数学公式、定理等，学生记得，但不知其成因.如向量数量积的坐标运算，由a=(x1,y1)，b=(x2,y2)，学生知道a·b=x1x2+y1y2，为什么呢？几乎无人知晓；余弦定理的公式，学生基本记得，怎么证明呢？很少有学生会；若问学生alogaN等于多少？不少学生知道等于N，什么原因呢？不知道.这类现象在高三一轮复习中，非常普遍.

现象之二：一些问题本应该有两个解题思路，而学生的方法却一边倒.如下题：

题：如图，海上有A,B两个小岛相距10 km，船O将保持观望A岛和B岛所成的视角为60°，现从船O上派下一只小艇沿BO方向驶至C处进行作业，且OC=BO.设AC=xkm.

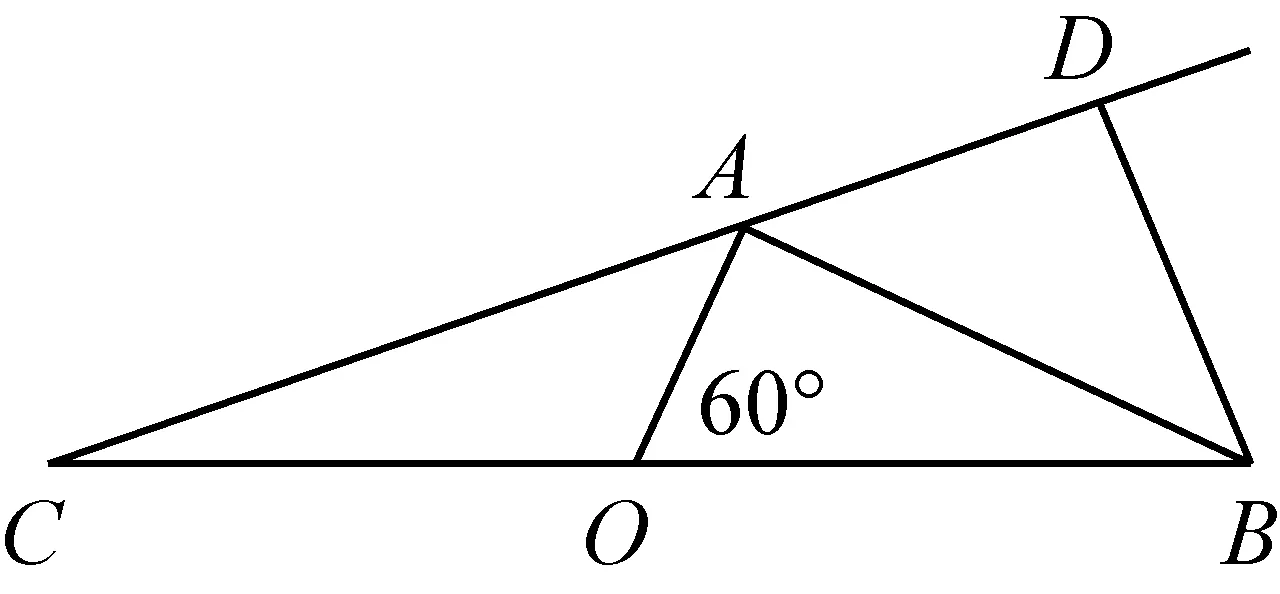
图

(1)用x分别表示OA2+OB2和OA·OB，并求出x的取值范围；

(2)晚上小艇在C处发出一道强烈的光线照射A岛，B岛至光线CA的距离为BD，求BD的最大值.

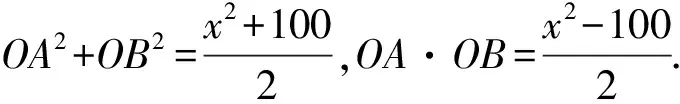
问题是第(2)小题，笔者所教班级只有3名学生完成了解答，全班没有发现1名学生建立坐标系，用解析法完成，他们的解析思想都哪里去了？真是令人匪夷所思！他们都是在寻求几何图形中的边角关系，而本题中的边角关系的建立较为灵活，使得绝大多数学生以失败告终.

2 原因分析

对现象之一，也许有人认为，这些数学结论，只要学生能灵活运用就行，能否理解其成因并不重要.这样的观点显然不妥，这是应试教育的典型表现.在高等数学中，确实有不少结论很难理解，要求学生记住，能套用公式就行，就像汽车驾驶员一样，只需要熟练掌握驾驶技术，而不需要掌握汽车原理一样.但中小学数学的内容简单，学生有必要理清其成因，其实，知识方法的本质搞不清楚，也很难灵活运用，就如现象之二，学生对解析法的本质理解不深，而无法把解析法用到几何问题的解答中去.此外，中小学数学的这点简单知识，都不弄清其内涵而建空中楼阁，学生将来怎能进一步深造学习？

那么，是什么原因造成上述两个现象的呢？是急功近利的思想在作怪.社会和教育主管部门对学校的高考期望值很高，学校向教师要高考成绩，加快教学进度，高中数学课程两年学完，高三一年复习.教师为了考试成绩，一些重点问题，反复讲，让学生反复练，因为现在的数学试卷题量偏大，要求学生快速反馈方法，并能熟练准确运算，这种教学方法的应试效果还就很好.其实，这种快节奏的教学方法，淡化了学生对数学内涵的理解，使我们的数学教学丢掉了根本！

新课程理念强调以学生为主体，得到了广大教师的认同，大多数课堂教学都注意引导学生思考，让学生学会解决问题.然而，依笔者看，过度引导的课堂教学比比皆是，不然，学生自己思考出来的东西，怎么到了高三就荡然无存的呢？纵观我们的一些公开课，课堂气氛活跃，教师问题一出，很多学生都能回答，全没有冷场现象，这正常吗？要么是学生已经预习过，他们就是说说答案而已；要么是教师的问题过细，千方百计让学生能回答他的问题，也就是笔者所讲的“过度引导”.学生的思考并不深刻，根本谈不上探究发现！试想，一个知识方法的构建，哪有这么容易？不少时间花在问题情境上，一半时间花在知识方法运用上，20分钟左右就生成一些重要的知识方法，难道我们的学生都是天才吗？当然不是，我们的学生到了高三，出现上述两种现象，也就不足为怪了.

3 教学案例分析

不知读者有没有注意到，一些快节奏教学的教师，他们所教班级平时成绩确实不错，然而高考成绩却平平，有时还不如人意，笔者所在学校确有此情况. 其原因很简单，很多知识方法快速生成，甚至直接告诉学生，速度快，课堂容量就大，学生成绩的提高见效快，但这是一种急功近利的短期效应，平时考试熟题多，这些班级的学生熟能生巧，分数高点，而高考有不少新题，这些班级的学生理解水平、分析能力并不强，分数就不高了.因此，笔者认为，不过度引导，真正以学生为主体，落实好探究教学，为促进学生的理解而教(见文[1])，这不仅对学生的高考成绩有帮助，对学生的终生发展大有裨益.以下结合一些具体的教学片段，谈谈笔者解决现象一、二的做法，与读者交流，以期抛砖引玉.

3.1 不过度引导 自然生成

知识方法的生成，重在“自然”.所谓自然生成，笔者是这样理解的，教师主要指明研究方向，以学生探究为主，尽量减少过程干预，通过学生的思考、以及合作交流，顺其自然地发现一些有价值的规律、定理等，教师再帮助学生总结归纳.如学习了正弦定理之后，怎样生成余弦定理呢？笔者将分析以下一个慢生成的教学过程.

问题1前几节课，我们通过探究发现了正弦定理，并且发现正弦定理在三角形中有广泛的应用，由此，同学们能联想到什么呢？

有些教师的课堂导入是：“前面我们已经学习过正弦定理，实际上还有余弦定理，本节课我将和大家一起来探讨余弦定理”.这就是过度引导，它严重削弱了学生的问题意识，是教师要求学生去找余弦定理，而问题1是要让学生想到余弦定理.如果学生长期在类似问题1的熏陶下，他们在发现正弦定理之后，很可能自己就会主动思考，是不是还有余弦定理和正切定理呢？有学习能力的学生，课后通过自主探究，自己发现余弦定理或正切定理，那才是更本真的自然生成！比学生多做几道关于“正、余弦定理”的题目，不知要强多少倍！只可惜我们现在的学生缺乏这种能力.

问题2既然同学们联想到了余弦定理和正切定理，那我们今天先来看看到底有没有余弦定理，是否有正切定理？大家课后再探讨.在三角形中，我们要去找余弦定理，有什么思路入手呢？请同学们交流研讨，看能不能找到探究思路？

如果我们课堂上，经常研讨类似问题2这种指向性不强的问题(特别是生源好的学校，更有必要)，学生的研究分析能力会大大增强.虽然难度比较大，但只要我们给足时间，学生还是能够找到解决方案的.既然是余弦定理，当然要侧重研究三角形内角的余弦了，那么如何研究三角形一个内角的余弦呢？

方案1：可以作高，在直角三角形中研究一个内角的余弦；

方案3：建立平面直角坐标系，可以利用三角函数的定义，也能研究一个内角的余弦；

至此，大约需要半节课左右的时间，但这费时的讨论是有意义的，学生自己思考出来的方法，他们印象深刻，记忆持久.剩下的半节课，让学生根据3个方案，自主解决发现余弦定理，学生代表交流发现余弦定理的过程，最后总结归纳余弦定理(其实，一些生源不好的学校，还未必能完成余弦定理的最终归纳).

也许有人会提出质疑，你这节课课堂结构不完整，没有余弦定理的运用.确实是没有运用余弦定理解决三角形问题，但不能说是没有运用，我们这里运用直角三角形的边角关系、运用向量的数量积、运用解析法等去研究三角形的一个内角的余弦，是实实在在的运用，而且是综合运用.余弦定理的运用放到下一节课，又何妨呢？慢一点，让余弦定理自然生成，使学生深刻理解余弦定理并经久不忘，这就是这节课的教学目标.

3.2 不过度引导 注重成因

方法的生成教学，其成因是关键，得有道理，否则学生只能生搬硬套，遇到新情境，就不能灵活运用了.上述现象之二，学生为什么想不到解析法？因为他们没有深刻解析法的内涵“用代数的方法解决几何问题”.新授课中，我们为什么要研究“直线与圆的方程”以及“椭圆的标准方程”，得分析清楚道理，才能建立起学生的解析思想.那么，“椭圆的标准方程”的新授课教学，如何帮助学生建立解析思想呢？

苏教版2-1“椭圆的标准方程”这节内容有一段引言，提出“汽车贮油罐的外轮廓线的形状像椭圆，是不是椭圆？”，“聚光灯泡的反射镜等仪器都是运用椭圆的性质制造的，怎样才能精确制造？”.随后指出，借助椭圆的方程，可以回答上述问题.(详见文[3])这是一种解析思想的建立，不能一带而过，我们要创造性地使用教材，让学生慢慢思考，逐步内化.

与教材一样，课堂导入从一些实际的椭圆问题入手，也可以替换一些问题，如“过椭圆上一点，怎样准确作出椭圆的切线呢？”，虽然高中阶段没有定义椭圆的切线，但学生肯定认可这样的问题.然后，提出如下问题引导学生思考.

问题1这几个问题，同学们能解决吗？(停顿)那这是一类什么样的问题呢？

前者，学生显然无法回答；后者，让人感到有点可笑，学生还不怎么好回答.其实，不就是几何问题吗？笔者的目的，就是要让学生知道，椭圆的学习，就是要研究椭圆这个几何图形的性质，为怎样研究椭圆的几何性质作铺垫.

问题2前面我们刚刚学习过椭圆的定义，现在就要我们研究椭圆的几何性质，同学们有思路吗？

如果教师直接告诉学生，借助椭圆的方程，我们可以研究椭圆的几何性质，可以解决上述问题，那就是照本宣科，就是过度引导，学生的解析思想就很难建立.事实上，如果学生在“直线与圆”的学习中，解析思想建立的好，就应该有不少学生能回答问题2，否则会冷场，没有学生能回答.假如是后者，我们还需要再进行问题的引导.

问题3请同学们思考：在初中，我们已经研究过三角形、四边形、圆等图形的性质，为什么高中阶段，我们还要学习直线与圆的方程呢？

读者试想：我们的学生能够回答这样的问题吗？他们的解析思想真的建立了吗？恐怕未必.初中阶段研究过这些基本图形，建立了一套定理体系，由此研究关于“多边形和圆”的更复杂的图形的几何性质，我们称之为“几何法”；而高中阶段学习“直线与圆的方程”，是用代数的方法研究与“直线和圆”相关图形的几何性质，是“解析法”.至于多边形，它是由线段构成的，只要研究直线的方程即可.

如此，再让学生思考问题2，就容易了.对于椭圆，才刚学习过它的定义，根本无法用几何法研究其几何性质，我们可以建立坐标系，研究其方程，通过方程计算处理研究几何性质.总之，这里教学一定要慢一点，多让学生思考，为什么要研究椭圆的方程？让学生领悟解析思想，知道解析法的用途，就是解决几何问题的，面对一个几何问题，我们有两个思考方向：一个是几何法；一个是解析法.这会耗去不少教学时间，知识的运用会减少，但这是根本，不能忽视.如果我们的学生只会做所谓的“解几题”，没有建立坐标系的几何题，他们只能想到几何法，那我们高中的数学教学是不是很失败呢？其实，哪有什么“解几题”？几何问题是客观存在的，坐标系是为了研究几何图形而人为建立的，是一种方法，是要我们去运用的.

3.3 不过度引导 突出分析

如果高一、高二将课堂节奏放慢，充分尊重学生的主体地位，不过度引导，以学生的探究发现为主，那么，学生对知识方法的理解水平必然有较大的提升.但我们面对的是不同层次的学生，总会存在一些学生理解不到位的情况，他们的知识方法或多或少还会存在一些漏洞，当然这些漏洞，在高三的复习教学中，我们还需要帮助学生弥补.高三教学不能仅仅是知识的回归，要深化理解知识体系；不能仅仅是题型的总结归纳以及机械重复的训练，要突出问题的分析，突出学生的思维过程，要让学生领悟方法的内涵，达到灵活运用的目的.纵观各类中学数学教学类杂志，发现有不少教师提出高三复习“一课一题”的教学方法，笔者非常认同这种教学方法，一节课强化分析一、两个问题，透彻理解其中所涉及的知识方法，有助于学生的灵活运用.就如上文现象之二的那道题，其中第(2)小题，学生的正确率很低，需要加强分析引导.

问题1在第(1)小题中，我们已经用x表示了OA2+OB2和OA·OB，并求出了变量x的范围，现在第(2)小题要研究BD的最大值，我们的解题目标是什么呢？

日常的备课组听课中，我们发现大多数教师的处理方法是，先请学生谈方法，并问学生：你是怎么想到这个方法的？让学生谈思维过程，教师帮助补充分析，然后进行方法的自总结归纳.对此，笔者认为有点操之过急，部分学生的解题方法及其思维过程，其他学生未必能顺利内化.有必要从解题方向上进行思维监控，让学生先从整体上把握解题方向，再进行具体分析.问题1，要学生分析解题目标，怎样求BD的最大值呢？第(1)小题选取了变量x，并求出其范围，因此，若能建立BD关于x的函数f(x)，就可以求其最大值.这既是一种理性分析，也是一种解题经验的分析，即要注意各个小题间的关联.

问题2怎样用变量x表示BD建立函数f(x)呢？我发现同学们都非常注重寻找图形中边角关系，但由于其复杂性，很多同学难以建立边角关系式而失败；只有少数同学找到了简洁的边角关系而迅速完成函数关系的建立.同学们注意，你们解决这个几何问题，缺少了一个方向性思考，你们再想想，少了一个什么解题方向？

现象之二说明学生解析思想建立的缺失，面对纯粹的几何题，想也不想就直接找边角关系而不能自拔，问题2的目的就是要让学生思考，对几何题而言，除了这种几何法外，还有另一个研究方向，用代数方法解决几何问题，即解析法.问题2的提问有点琐碎，但简洁的提问，学生又无从思考，如“这样的几何问题，我们有哪些思考方向呢？”，学生往往只回答自己的思考方法，不得已，统称为“边角关系的思考”即几何法，这样再让他们思考另一个解题方向，目的是要让他们恍然大悟，原来我们忘记了一个重要的方法，即“解析法”.最后作方向性思考的总结，面对一道纯粹的几何题，我们应有两个解题方向，一是几何法，侧重于几何关系的建立，以寻找边角关系为主；二是解析法，侧重于代数运算，主要是建立坐标系，以坐标运算为主.当然，几何法与解析法也不是完全割裂的，如坐标系下研究直线与圆的问题，我们也可以适当运用一些圆的基本性质，以简化运算.

问题2的研究后，先让学生用解析法完成这道题，要让他们体会解析法的思路，思路很清晰，运算也不很难，要让他们知道，解决问题不能一棵树上吊死，要多方向思考.最后，再让部分学生谈谈几何法的思考过程，教师作一些总结性分析等等.

4 几点反思

两个现象的发现，以及几个教学案例的分析，笔者对高中数学教学有以下几点思考，与读者研讨，以期抛砖引玉.

(1)数学教学，不要丢掉根本.让学生掌握基本数学知识和重要的数学思想方法，并学会运用这些基本知识方法思考解决问题，是我们数学教学的重要任务，这些知识方法的生成过程是教学的根本，如果高考之后，学生不从事数学方面的学习工作，他们高中所学习的知识方法很快就遗忘了，那其实就是根本不牢.笔者对高中阶段数学归纳法的学习，一直历历在目，记得有一节课，我们高二数学老师，在黑板上画了一排小矩形，他问道：假设这是一排砖块，现在要让它们全部倒下，需要满足什么条件呢？然后让我们讨论，学生代表发言，教师提取有效信息总结数学归纳法，课堂气氛很活跃.这其实就是现在的探究教学理念，教学效果很好，那为什么现在还会出现上述现象之一的呢？可能与我们问题过细、引导过度有关；与我们舍不得花时间让学生讨论有关，大型公开课还行，平时上课只是象征性地让学生讨论，要节省时间进行知识方法的运用.其实，我们教师不缺少教学理念，只要我们合理创设教学情境，合理设问，让学生充分思考，应该不会丢失数学根本.

(2)让课堂节奏慢下来，促进学生的理解.不知读者有没有注意这样一个现象，当我们与考试有问题的学生交流时，有不少学生都表示上课听得懂，这就是我们所讲的“懂而不会”的现象.为什么会出现这种现象呢？学生虽然听懂了知识方法，但他们未必真懂其内涵，“依葫芦画瓢”还行，问题一变，就不能灵活运用了.因此，我们的课堂教学不仅仅是让学生听得懂，还要让学生真正地理解，有必要让课堂节奏慢下来，认真落实课程理念，尊重学生、注重探究教学.知识方法的生成，不能引导过度，要不惜时间充分引导学生自主发现，他们的理解自然深刻，不仅能记忆持久，还能激发学生的探究热情；例题教学要少而精，题型讲得多，学生见识广，短时间内可能有效，时间一长，仍然不会，不如一节课只讲一、两个问题，引导学生学会思考，真正把问题研究透彻了，这样逐步培养学生解决问题的能力，即使问题变化，但所用的知识方法不变，他们还是能够解决.

(3)提高自身的专业素养.一名数学教师要教好学生，要具备两个条件：一是要有较强的专业素养，仅仅会解题是不够的，要能站得高看得远，他所教的学生才能视野开阔，问题的认识才深刻；二是要会教，要有较强的教育教学理论知识，要有先进的教学理念，他所教的学生接受能力才强，接受速度才快.因此，我们要积极参加一些正规的教学研讨活动，多聆听那些专家的教学指导；要多阅读一些数学专业书籍，加强自身的认识水平；要多订阅一些中学数学教学类杂志，拓宽视野，一节数学内容，大家都教过，人家却整理发表了，与我们日常的教法有什么不同？一个数学问题，我们都研究过，为什么人家能成文发表？作者的理解比我们深刻吗？多学习、多研究，我们的专业素养定能提高，我们教出的学生定能更优秀！