古罗马建筑艺术中的数学文化——以维特鲁威的《建筑十书》为例

王 敏 代 钦

(内蒙古师范大学科学技术史研究院 010022)

1 前言

建筑发展的历史也是一部人类生活文化史，是建筑艺术与理论知识积累的历史.不同的历史时期，有着不同的建筑式样，纵观古今中外几千年建筑艺术的杰作，体验历代建筑艺术大师丰富的建筑理论与经验，就会发现一座活的建筑，其中蕴含着丰富的人类学、哲学、美学、数学与机械等知识.所以对于建筑师而言，不再只是建造了一座建筑物，同时还形成了自己的理论.从数学文化的角度剖析，建筑艺术中蕴含着丰富的数学文化，其中理性的、抽象的、基于数学的研究方法能对建筑设计有所裨益，同时许多建筑师也提出要以数学方法表达建筑造型的可能性.另外对于建筑艺术中的诸多之谜，可以从数学的角度去解释，如埃及的金字塔中，齐奥普斯金字塔几乎是精确的等边三角形，塔身与周边的倾角为51°—52°，而齐夫伦金字塔的塔基是一个十分精确的正方形.[注][英]帕瑞克·纽金斯.世界建筑艺术史[M].顾孟潮，张百平，译.合肥：安徽科学技术出版社，1990：35.维特鲁威的《建筑十书》是西方古典时代唯一幸存下来的建筑全书，对其有“一部西方建筑史就是一部维特鲁威的接受史”[注][古罗马]维特鲁威.建筑十书[M].[美]I.D.罗兰，英译，[美]T.N.豪，评注，陈平，译.北京：北京大学出版社，2012：封皮.的评价.维特鲁威的手稿被罗马教廷波基奥(G.F.Poggio)在瑞士的圣盖尔(St Gall)图书馆发现的，并于1451年完成译本，在1487年，维特鲁威成为当时第一批以印刷作品问世的作者之一，其影响是巨大的，新的交流手段使得建筑艺术从泥瓦工拜师学艺的经验传统的延续，变成了一种文艺上的构想.文中以维特鲁威的《建筑十书》为例，分析其中的数学知识，体验其中的数学文化.

2 维特鲁威及其《建筑十书》简介

马尔库斯·维特鲁威·波利奥(Marcus Vitruvius Pollio)，公元前1世纪生活于罗马共和制向帝制过渡的重要转折时期，他是一个“保守主义者”，不遗余力地维护从古希腊传承下来的人文价值观和建筑理想.他的父母给予了他较为宽泛的“自由艺术”教育，同时也接受了赖以谋生的职业教育，但他的学识靠的是自己终身学习，或利用自己的藏书，或利用富人和当权者的图书馆，另外，他还熟习一些技术，并且坚持认为技术如果没有文学及综合一切知识是不能被验证的.所以，维特鲁威的课程表中，有绘画、几何学、算术、光学、历史学、哲学、音乐、医学、法律、天文学、古典语言学、写作以及古文献学，他强调一个人不可能成为所有学科的专家，但掌握这些学科的基础知识是至关重要的.维特鲁威认为，要成为一名理想的建筑师，应该洞察自然物性和人生真谛，要掌握广泛的知识，他的这一想法对于后人的影响是深远的，如文艺复兴时期的“文艺巨匠”——列奥纳多·达·芬奇.总之，维特鲁威重视基础教育，强调终身学习，为提升建筑师的社会地位，他为建筑师的教育努力奋斗，以他的博学与才干为世人提供了理想建筑师的楷模.

维特鲁威的《建筑十书》是欧洲中世纪以前遗留下来的唯一一本建筑学专著，这本书后来成为文艺复兴时期(14世纪—17世纪)、巴洛克时期(17世纪—18世纪)和新古典主义时期(18世纪末—19世纪)建筑界的经典，并且至今仍对建筑学界产生着深远的影响.《建筑十书》主要是一本建筑技术手册，从城市的选址、建筑的类型、建筑的材料一直延伸到施工机械和构件的细节，但是其中有一半以上的内容并非论述建筑本身，而是讨论一些与此相关的基础知识，如数学、天文学、地理学和自然哲学等.由于其涉及领域广泛、内容丰富，被称为一部真正的“古代文化百科全书”.

在建筑技术如此发达的今天，东西方学者对它的翻译和研究仍络绎不绝，因为不管在建筑学还是其他学科领域，人们都不仅将其视为一本古代科技著作，对它抱有一种实用主义的态度，而且更多地关注其文化史意义，以及书中强调的建筑师的教育、知识的统一性、建筑的意蕴、理论与实践的关系、建筑与社会伦理、人类健康与环境等问题.

《建筑十书》的主题涉及两个方面：一是“建筑”的范围涵盖整个营造和机械领域，是一门综合性很强的艺术，也是社会人文艺术中最基本的艺术形式之一；二是真正意义上的建筑实践是建立在综合把握范围广阔的理论与实践知识的基础上的.[注][古罗马]维特鲁威.建筑十书[M].[美]I.D.罗兰，英译，[美]T.N.豪，评注，陈平，译.北京：北京大学出版社，2012：53.它不只是一本指导罗马建筑师如何去接受训练和实践的书，而更像是提出一种主张去教导建筑师该如何实践的一本书.

图1 1684年画作，维特鲁威(右)向奥古斯都大帝展示《建筑十书》.

3 《建筑十书》中的数学文化

3.1 数字发明于人体四肢

古希腊哲学家普洛塔高瑞斯(Protagoras)曾说过：“人是万物的尺度.”[注][英]帕瑞克·纽金斯.世界建筑艺术史[M].顾孟潮，张百平，译.合肥：安徽科学技术出版社，1990：228. [英]萨拉·巴特利特.符号中的历史[M].范明英，王敏雯，译.北京：北京联合出版公司，2016：179.对人类本身的关注与研究是设计的前提，“以人为本”的观念，更是维特鲁威建筑设计的首要理念.测量作为工程建筑中必不可少的步骤之一，在建筑设计中非常重要.维特鲁威汲取了毕达哥拉斯学派及其他一些数学家的观点，认为测量的单位来源于人体，如，指、掌、足、肘等.毕达哥拉斯学派的神秘数论认为“十”为完美数，因为完美的双手手指为十个.并且十是由最初的一二三四相加而构成的，在古希腊，十是由四个被称为单位的元素相加得出的，一旦得出十一或十二，就超过了“十”并且超过了四个一组的四，便不再是完美数，直到下一个十，最初的四个数就是完美数的构成单位.

图2

然而，还有一些数学家认为“六”才是完美数，因为这个数中包含了六个单位，他们的比值又与数字六相吻合.如，六的六分之一等于一，六的三分之一等于二，六的二分之一等于三，六的三分之二等于四，六的六分之五等于五，尽善尽美的数字便是六.六为完美数字的另一个解释就是：1+2+3=6,1·2·3=6.如果再加上另一个单位，使数字向六的双倍增加，即给六加上它的六分之一便是七；到八时，给六加上它的三分之一；给六加上它的二分之一便得到了九个单位，等等.又因为他们认为脚长是人体身高的六分之一，该数使得脚的尺寸完美起来，乘以六便得出人体的身高，所以他们坚持认为六这个数字是完美数.

维特鲁威经过对常见事物的观察，研习前人的研究，将六和十这两个完美的数字加起来，得出最完美的数字十六.这项发明起源于脚，按照古人的观察，肘是由六掌或二十指构成的，如果一肘中扣除两掌，余下的四掌等于一足，每掌由四指组成，由此得出一足为十六指，具体如图2所示.于是，维特鲁威指出，按照大自然对人体尺寸的安排，测量中常用的单位为：四指为一掌，四掌为一足，六掌为一肘，四肘为人身高.

3.2 几何学——建筑师的必修课

自古希腊以后，几何学成为西方理性思想和科学精神的根基，建筑思想和技术亦不例外，也以几何学为主要工具来实现其设计.建筑师要掌握识字、绘图的基本技能，但是要想得心应手地用图形来表现想要建造的作品的外观，几何学的知识是必不可少的.几何学对建筑助益良多，它传承了圆规与直尺的技术，有助于实施现场的平面布局，画出直角线、水平线和直线等.

图3

神庙作为西方不朽之神的神圣居所，在西方建筑史中占有重要地位，维特鲁威在第3书中对其设计方法进行了说明，神庙设计的基本原理决定了其平面形式，其中大多数以柱形为主要表现形式，那么圆柱就成为大多神庙中的主要设计.圆柱的柱槽为二十四条[注]意思是将一个圆划分成二十四等份，再从一个六边形开始逐渐对它的各个边进行对分，便可以做到这一点.，它向内凹进，若将直尺置于槽沟内并转动，直尺的角便会触及柱槽左右边缘(如图3).[注][古罗马]维特鲁威.建筑十书[M].[美]I.D.罗兰，英译，[美]T.N.豪，评注，陈平，译.北京：北京大学出版社，2012：97.维特鲁威的这一设计是对公元前6世纪初“泰勒斯定理”的一个推论的应用，相传米利都的泰勒斯证明了现称“泰勒斯定理”的命题：半圆上的圆周角是直角.而维特鲁威在对圆柱中槽沟的设计中演示证明了泰勒斯定理的推论.即“所有内接于圆的三角形，直径为斜边，均为直角三角形.”

图4

西方古代计算上的麻烦导致古代的建筑师宁可采用几何学的方法而非计算的方法来思考问题[注]这是因为毕达哥拉斯学派发现无理数后之后，其“万物皆数”思想受到不可换回的冲击后，他们认为计算不可靠，只有几何证明才可靠.从那时起直到笛卡尔创立解析几何，极端崇尚几何学的这一思想才逐渐减弱.，如，在维特鲁威的《建筑十书》中，他改写了柏拉图《美诺篇》中所记述的一段轶事，即苏格拉底引导无知的奴隶推算正方形面积加倍的基本原理，具体内容如下：

有一块正方形的土地，十足长十足宽，面积100平方足.如果需要使它的面积翻倍，成为一块200平方足的土地，同时保持各边相等，问题便是，这正方形的边长应该是多少，从而使这翻倍的面积等于200平方足.

如前所述，维特鲁威称通过计算是不可能求出的，所以他按照柏拉图面积倍增的方法给出了几何的解法(如图4所示)，即在原先边长为十足的正方形内划一条对角线，将它分为面积相等的两个三角形，每个三角形的面积为五十平方足，然后再以这条对角线为边长画一个正方形，于是，无论一个较小的正方形中的对角线所划定的两个三角形的尺寸是多少，每个三角形的面积均为五十平方足，同理，在较大的正方形中便创建出了四个大小相等的三角形.显然维特鲁威应用了正方形的两条对角线将其分成四个面积相等的等腰直角三角形，然后用五十平方足的三角形还原成正方形的方法即将原来的正方形的面积增倍.

另外，毕达哥拉斯学派发现和证明了“角尺的原理”(即毕达哥拉斯定理)后，维特鲁威面对工匠们做出的不精确角尺，根据毕达哥拉斯所发现的定理，按照下面的方式做了一把角尺：他先取了三根直尺，一根三足长，另一根四足长，第三根五足长，将它们拼在一起，使其端部互相接触，形成一个三角形，便做成了一个完美的角尺板(如图5).同时，维特鲁威发现：边长为三足与四足的两个正方形的面积之和，就相当于[注]“相当于”就是“等于”的意思.边长为五足的正方形的面积.[注][古罗马]维特鲁威.建筑十书[M].[美]I.D.罗兰，英译，[美]T.N.豪，评注，陈平，译.北京：北京大学出版社，2012：156.

这些原理在许多测量中都有用处，维特鲁威将其运用到建造楼梯时计算倾斜角，他将最上部的托梁到下面地板之间的楼层高度划分为三等份，那么楼梯坡度的合适长度便是五等份，所以维特鲁威强调不管托梁与地面之间的三等份的尺寸是多少，楼梯的水平长度都为四等份，这样就可以准确确定出台阶的位置，具体设计如图6所示.

图5

图6

3.3 比例思想研究的源头之一

建筑设计有它固有的、天生的比例方法.[注][丹麦]S.E.拉斯姆森.建筑体验[M].刘亚芬，译.北京：中国建筑工业出版社，1990：111.维特鲁威的《建筑十书》内容涉及建筑学中制图的基本原理及方法，比例思想是其中应用最广泛的内容，在第3书和第4书中都涉及到比例问题，维特鲁威在开篇就给出了比例的定义：“比例就是建筑中每一构件之间以及与整体之间相互关系的校验.”[注][古罗马]维特鲁威.建筑十书[M].[美]I.D.罗兰，英译，[美]T.N.豪，评注，陈平，译.北京：北京大学出版社，2012：90.由于古代西方没有统一的度量单位，比例在建筑学中的应用就显得异常重要，维特鲁威主要涉及两方面的比例问题，一是把人体的自然比例应用到建筑的丈量中；一是在神庙建筑中由比例产生均衡.

图7

图8

另外，神庙建造的重要部分——圆柱的设计对于神庙体系的完备是十分重要的.圆柱的设计包括圆柱的高度、直径以及柱头与柱础的高度等，维特鲁威给出的比例体系有两种方式：一种是直径是一定的，降低圆柱的高度从而增加柱距或跨度；一种是圆柱的高度不变，增加圆柱的直径减少圆柱之间的跨度.所以，圆柱顶端柱颈的收分必须按照如图8设计，具体的比例分配如表1所示.

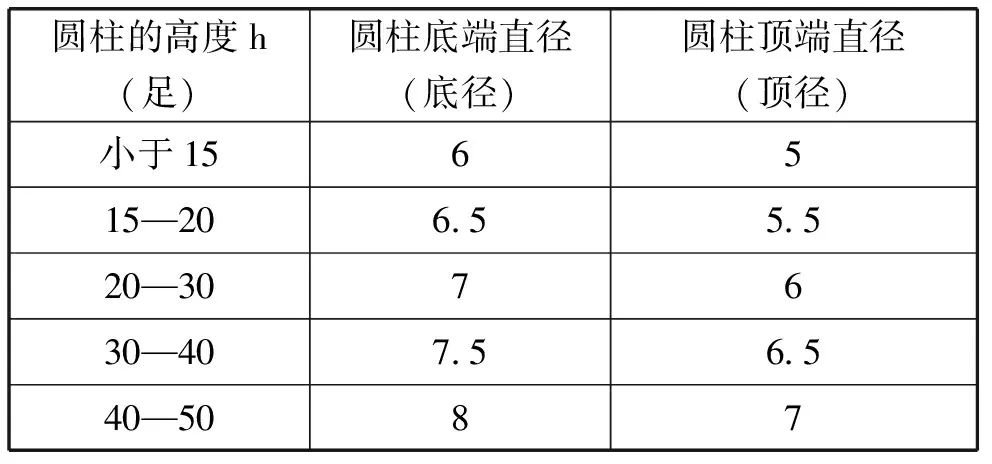
表1 圆柱设计中各部分比例分配表

若圆柱比五十足更高，则根据相同的原理对柱颈进行收分.这样运用比例的理论对建筑物进行的设计仍有许多，如圆柱间距与圆柱直径之间的比例以及柱头与柱础的高度与柱高的关系等.只要按照规定比例进行的设计在维特鲁威的建筑学中才是合理的.这些圆柱设计中的比例关系，在之后柱子的设计中都能找到，如帕拉第奥别墅中的古典式柱子的设计，其中柱子的划分直到最微小部分的设计都有定则，其基本的单位是柱径，不仅柱身柱头及柱础的尺寸都由柱径演算而得，而且连柱子上所有线盘的部分及柱距都由此得到.

4 结语

建筑艺术作为人类艺术宝库中的瑰宝之一，其中蕴含着丰富的哲学、天文学、地理学等知识，作为“古代文化百科全书”的《建筑十书》被誉为西方建筑理论的源头.在学科划分越来越细专业林立的今天，从数学文化的视角回顾其中的文化意义、科学内容、通识教育和知识统一等观念，会使我们得到教益.同时领略维特鲁威的建筑学体系中从古老的毕达哥拉斯、赫拉克利特、亚里士多德等那里所借鉴的丰富哲学和数学，也足以窥见古希腊学者对数学的深刻研究以及数学作为一门古老学科的广泛应用性，同时将人体比例与建筑比例的完美结合也体现了数学知识的自然观及神秘性.

在以往数学文化、数学史方面的论著中涉及建筑学方面的内容也不少，在中小学数学教学中数学文化的融合已不再少见，维特鲁威《建筑十书》中的诸多案例也可以融入中小学数学教学中，如小学生认识数字的教学，可以引用维特鲁威的观点，测量的单位来源于人体.通过对人体各部位的测量及度量其中的关系，更加形象地认识数字，同时维特鲁威按照人体尺寸给出的测量常用单位的介绍，可以使得学生更好地对数字的大小有估算意识，进而培养学生的数感.另外，通过在校本课程或数学活动课中讲授维特鲁威利用毕达哥拉斯定理制作角尺的过程，更好地理解毕氏定理的应用.神庙建造中的圆柱设计中比例思想的应用也可以使学生认识到数学应用的广泛性.