对数学问题2134的整理与探索
2017-12-24 13:35:18季潮丞
数学通报 2017年5期
季潮丞
(浙江省宁波中学 315100)
《数学通报》2013年第7期第2134号数学问题引起广泛关注,其中安振平老师在他的博客[5]中对该问题有多种有别于本刊[1]的证明.特别罗列了张云华、熊昌进老师的独立证明.本人也学习了这些老师的解答,并参考了相应文献,有体会如下.
问题a,b,c是满足(a+b+c-2)2=2abc的任意实数,
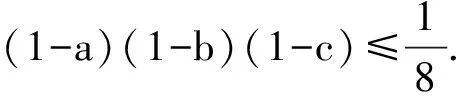
证明设1-a=x,1-b=y,1-c=z,则原问题等价于

下面利用基本不等式和简单的分类就可以得到证明,详见[1],[5].
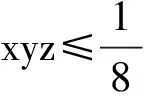

笔者通过对上述问题的研究并了参考文献[2],[3],[4],提出以下不等式:
已知x,y,z为非负实数,且满足x2+y2+z2+2xyz=1,

证明由原问题易知(1)成立;
由x2+y2+z2=1-2xyz及(1)知(3)成立;
由x2+y2+z2≥yz+zx+xy知不等式(4)要强于(2),下面证明(4):

即
cosBcosC+cosCcosA+cosAcosB
由室内考种表可见,使用免耕机械处理的产量明显高于对照,亩增产46.4kg。虫食率下降1.4个百分点,单株荚数增加9.5个,单株粒数增加15.2个,增产率为30.5%
不妨设A为最大角,则1-2cosA≥0,

事实上,运用琴生不等式易知
2cosBcosC=cos(B+C)+cos(B-C)
≤1-cosA.
所以(4)成立.
z2+2cosAcosBz+cos2A+cos2B-1=0.
解上述方程得
z=cos(π-A-B)或-cos(A-B),
由于z∈[0,1]所以z=cos(π-A-B),在此我们设C=π-A-B.综上可知换元是等价的.

《数学通报》2013年第7期第2134号数学问题相关的内容还有很多丰富多彩的地方,作者限于篇幅无法详述,请读者参考文献[2],[3],[4].
猜你喜欢
中学数学研究(2024年4期)2024-05-23 13:15:19
中学生数理化·七年级数学人教版(2023年3期)2023-03-21 00:45:16
聊城大学学报(自然科学版)(2022年2期)2022-11-19 07:03:54
数理天地(高中版)(2022年9期)2022-07-24 05:56:01
中学生数理化·七年级数学人教版(2018年3期)2018-05-30 06:58:13
中文信息(2017年12期)2018-01-27 08:22:58
戏曲研究(2017年3期)2018-01-23 02:50:52
中学生数理化·中考版(2017年3期)2017-11-09 02:07:30
中学生数理化·七年级数学人教版(2016年2期)2016-05-30 21:20:57
中央民族大学学报(自然科学版)(2015年2期)2015-06-09 08:45:18

