谈数学课堂的有效设问
陈 樑
(绍兴市稽山中学 312000)
课堂设问是数学课堂中师生互动的重要途径,是师生间交流的“桥梁”.课堂设问有助于培养学生的数学思维,树立问题意识,激发积极思考问题的能力,同时还能活跃课堂气氛,控制教学时间.
因此,课堂设问功能是多样的,有效的课堂设问是一门艺术,艺术讲究多彩,但在设计时还需讲究严谨.有效的课堂设问,受问题的内容、设问的形式以及学生的参与度等因素的影响,教师在进行课堂设问时,需要严谨对待.
近日,笔者连续听了两堂校本研讨课,课题“数系的扩充和复数的概念”.听后,笔者最大的感想是:一节有效的数学课,离不开一系列教师设计的有效设问.同样的教学内容采用不同的设问,以及相同的设问内容,不同的教师采用不同教学方式、教学语言和表现形式进行设问,所得到的效果是截然不同的.
1 有效不有效,在于问什么、怎么问
换言之,这就是我们常提的“注重问题质量”,也是实现课堂有效设问的关键因素.如何在教学实践中保证问题质量,笔者总结出以下几点:
(1)问题内容必须是清楚的
在《数系的扩充和复数的概念》这节课中,当课堂进行至“给出复数一般形式z=a+bi(a,b∈R)”前,教师需要作适当引导.其中教师A设计了如下课堂片段.
片段1:
师A:……我们把i叫做虚数单位,且i2=-1.……我们规定i可以与实数进行四则运算(板书),相当于我们可以把i看成一般的实数,可以与其他实数进行运算.
那么,现在请同学们列出几个关于i的运算结果.
(教室里鸦雀无声,学生有点无所适从,不知从何入手)
师A:我的意思是,给出几个i参与的运算结果.比如1+i就是一个结果.请同学回答一下.
生1:(怯生生地)2加上i等于2+i.(显然错误理解了教师的设计意图)
(教室里哄堂大笑,师A和生1都感觉到很尴尬)
(师A又点了几名学生回答,感觉都不满意)
师A:其实我的意思很简单,就是给出几个有i的结果就可以了,比如2i,-3i,-6+i,1-7i……
(哦,原来如此!教室里发出会意的声音)
至此,笔者也和在座学生一样,才刚刚领会了师A设计问题的意图是为给出复数一般形式z=a+bi(a,b∈R)作引导,但显然设计并未达到预期目的.
反思:问题的给出并不很自然,内容本身很模糊,学生很难入手.课堂设问必须要让学生清楚“问的是什么”!学生学习本课之前尚未接触过i这个虚数单位,单凭一句“我们规定i可以与实数进行四则运算”,学生是无法体会到的,更何况是列出几个关于i的结果了.
该教师的课堂设问失败,从根本上探究是低效.低效设问往往表现为问题内容极端化,集中体现在两点:(i)教师设置问题太直观,答案很容易得出;(ii)问题设置过偏过难,学生无法把握教师设问的意图.种种如是,是将学生排斥在课堂之外,课堂效果也无从谈起.
(2)问题的内容必须存在价值
在《数系的扩充和复数的概念》的另一节课中,教师B在面临同样的课堂设问“引导学生“给出复数一般形式z=a+bi(a,b∈R)”时,他设计的片段则十分精彩.
片段2:
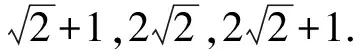
………………
师B:问题二 现有实数集合和i,你能构造出更多的数吗?
(有了问题一的铺垫,学生们都跃跃欲试)

……
师B 很顺利地给出了复数的一般形式.
反思:本片段体现教师B对问题价值判断准确的能力.问题一和问题二相呼应,问题一作为问题二的铺垫,可以说是辅助问题,但对于整个问题串的提出相当有效,这正体现了问题本身的价值.学生参与其中,关键是思维参与了问题,而该问题具有一定的开放性,给学生广阔的思维空间.
问题是否有价值,与学生的思维量有关,与学生的积极性和主动性有关.一些概念性的问题再现和非推理性的问题是简单而低级的,学生并未通过积极深入思考,而采用简单记忆和复述而回答问题,设问题将真成为了“问题”,而课堂将成为传统教学模式下的课堂.
2 有效不有效,在于能倾听、反馈
设问不能浮于表面,注重形式,提个问题,叫个学生回答,再把自己准备的结论展示出来,这纯粹是浪费宝贵的课堂时间.许多教师对于一些学生不经意间展现出来的智慧闪光点或者一些智慧资源不理不问,无视学生的情感培养,把课堂当作展示备课内容的平台而忽略了课堂是师生交流知识情感交流的舞台.
在片段1中有一个细节:生1怯生生地回答“2加上i=2+i”,这个回答虽然不符合课堂需要,达不到教师设计意图,但此时教师若能认真体会生1 的回答,取其结果“2+i”而省去运算式“2加i”,那么几乎所有参与课堂的人将马上意识到教师的设计意图,而课堂也不会在后续讨论中陷入尴尬.然而令人遗憾的是,师A一味地点名设问其他学生,“执着”地等待出现设计意图中的答案.这对于当事学生乃至整个课堂应该算是一个沉重的心理打击.
再来看片段3:
师B:问题三 请你列举几个复数,并说出它们的实部和虚部.
师B:(教师此时马上追问)哪里出现过了?
生1:第一个i+4.
师B:你认为出现过了的意思是这两个数字i+4和4+i是一样的?
生1:是呀!
师B:那什么叫做两个复数一样?
生1:……
师B:我们所熟悉的两个实数一样,实际上是这两个数字……
生1:相等!
师B:对!两个复数一样就是两个复数相等,那如何定义两个复数相等?
生1:实部与实部相等,虚部与虚部相等!
……
反思:多么机智的老师!老师认真倾听学生的回答,包括学生的错误回答.老师面对学生错误并没有及时纠正其或者任其自我纠正,却采取紧急追问法,把思路引导到两个复数相等的讨论上来,既帮助学生下了“台阶”,又十分自然地引出了下一问题.
课堂的预设是很重要,但不是决定性的,课堂的实际和预设会存在偏差,这是很正常的,教师要具备课堂驾驭能力,关键是具备临场应变能力.一些出乎意料的场面或者是一些小意外,在一些教师面前是尴尬,但在更多的教师面前可能就是机遇,这些小尴尬往往是课堂有效教学的生成点.教师需要做的是借助与学生的交流,找到学生的观点,根据数学学科的特点,把握学生思维活动的恰当时机.
3 有效不有效,在于会讨论
数学课堂面向的是全体学生,但课堂设问又只是针对个人,教师往往将课堂知识联结点设置为某个学生回答出教师预期中的答案.如果这位学生回答错误,则请下一位学生作答,直到正确答案出现为止.在这中间,学生正确与否全由教师一人来评定,而其他学生充当“看客”.学生参与度不高,思维量不大,有效性大打折扣.
片段4:
师A:好,下面请同学来小结一下,本节课你学到了那些知识?
(教室内仍然鸦雀无声,有的低下了头,有的似乎在思考,1分钟过后,师A点名请生1回答)
生1:这节课我们学习了虚数单位和复数.
师A:还有呢?
生1:学习了虚数和实数组成了复数.
师A:还有呢?
生1:还有……
(教室内气氛很尴尬也很僵硬,空气似乎凝固了)
师A:请坐,这节课我们还学习了……
片段5:
师B:问题六 比较一下复数与实数有什么不同,你认为在处理复数问题时通常会采用什么方法?
(学生分组前后左右4人讨论,时间3分钟)
生1:我们认为复数的范围比实数大,而且复数形式上比实数复杂,所以处理复数的时候要分清楚是实数还是虚数,如果是虚数,就要分析是否是纯虚数,所以要同时考虑实部和虚部!这样考虑起来将比较麻烦.这叫“分而治之”的方法.
生2:我们认为复数是实数的推广,是实数集合的扩充.我认为在处理复数的时候要同时考虑两方面问题即实部和虚部,而实数只要考虑单方面问题就可以了.虽然复数看上去考虑的部分多,但由于实部和虚部都是实数,处理起来未必如生1所说那样麻烦.
生3:两方面考虑毕竟比单方面考虑要麻烦点!
师B:我们学过的知识中有没有要同时考虑两方面的问题的?
生4:有,向量,还有坐标,还有曲线的方程……
师B:很好!……
反思:笔者非常反对课堂设问结果由教师评定,其实学生评判问题结论,是其数学思维训练的结果,是数学思想方法集中应用的体现,是是非辨别能力的培养,也是一个辩论能力的提高的过程.教师的设问,可以让学生小组讨论、辩论,也可以是师生之间讨论、辩论.这种形式看上去会浪费不少时间,但是通过这样的个体反思和集体探讨,培养了学生自主参与意识,反而提高了课堂设问的效率,增强了设问的有效性.
通过对两堂课的认真比较学习,我们认为有效的课堂设问还应做到:1.多给学生一些思考问题的时间;2.鼓励学生多向老师设问,而不是总是老师设问学生;3.多设问一些开放性的问题,对于一些记忆性的层次较低的、特别是低效甚至是无效的问题要尽可能避免提及等等.
在新课程实施过程中,作为新时期的数学教师应该在课前认真设计好问题串,利用数学课堂设问的一些技巧,合理设问,启发学生;鼓励学生更多更有效地参与课堂,培养学生基本数学素养和数学思想,争取把学生培养成为具有实践能力和创新精神的人才.

