一道IMO平面几何试题的形变探究

杨标桂

(福建师范大学数学与计算机科学学院 350117)

1 问题背景

问题1[1]设J为△ABC顶点A所对旁切圆的圆心. 该旁切圆与边BC相切于点M，与直线AB和AC分别相切于点K和L. 直线LM和BJ相交于点F，直线KM与CJ相交于点G. 设S是直线AF和BC的交点，T是直线AG和BC的交点. 证明：M是线段ST的中点.(2012年第53届IMO试题)

分析: 如图1，只须证明MJ是线段ST的垂直平分线，也只须证明△JST是等腰三角形且JS=JT. 问题的难点就是如何定位点F,G. 于是自然考察△BFM，数量分析如下：

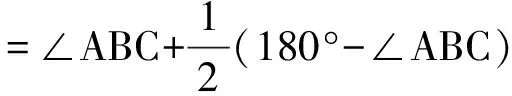
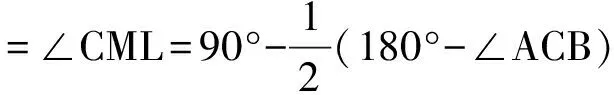
因此

∠BFM=180°-∠BMF-∠MBF

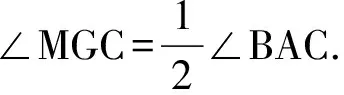
从而A,L,J,F和A,K,J,G都四点共圆，并且都以AJ为直径，故A,F,K,J,L,G六点共圆. 再考察S,T两点的位置如何确定. 在△BAS中，BF⊥AS，且BF平分∠ABS，从而BF是AS的中垂线，于是JA=JS. 同理JA=JT. 所以JS=JT.

至此问题已获解决.

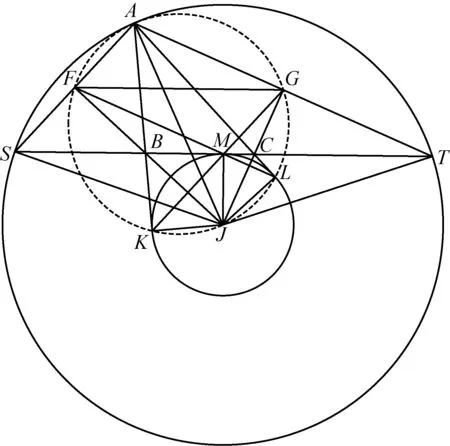
图1

同时，我们还可以发现了不少好的结果，比如:

(1)A,F,K,J,L,G六点共圆;

(2)M,J,S,F及M,J,T,G皆四点共圆;

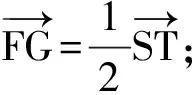
(4) 四边形AFMG是平行四边形.

问题到此是不是结束了呢？笔者认为，解题后的反思是一件非常必要而有意义的事情，问题还能得到什么引申结果？问题还有什么别的证明方法？问题形变以后又可以得到什么新的结果？下面我们将研究这道试题的形变问题.

2 问题形变

上面问题给出了三角形一个旁心所对应的性质，于是自然想到其他两个旁心也有类似的性质，由局部到整体，我们可以考察旁心三角形，希望探究出一些新的有趣性质. 为了使得字母符号具有轮换性，我们对问题1的构形图中的字母符号表示作一些调整.

问题2如图2，在△ABC中，I1,I2,I3分别为顶点A,B,C所对的旁心，于是△I1I2I3是△ABC的旁心三角形，且旁切圆Ii分别与△ABC的三边BC,CA,AB所在的直线相切于点Ai,Bi,Ci，i=1,2,3. 设线段B1C1分别交线段I1I2,I1I3于点U2,V3，线段C2A2分别交线段I2I3,I2I1于点U3,V1，线段A3B3分别交线段I3I1,I3I2于点U1,V2. 求证:U1,U2,U3,V1,V2,V3六点共圆.

图2

这个结论是怎么得到的呢？关键也是分析U1,U2,U3,V1,V2,V3这六点的位置.笔者感觉，有些平面几何题之所以难，就是我们对问题中的某些特殊点的位置难以把握，不知道如何重新定位它们. 从下面我们结合问题1来分析.

事实上，点U1,V1其实就是问题1中的F,G. 也就是我们有：

I1I3∩A3B3=U1=I1B∩A1B1，I1I2∩A2C2=V1=I1C∩A1C1.

U2,V2和U3,V3的位置类似得到.

利用问题1所得到的引申结论(3), 问题2中的U1,U2,U3,V1,V2,V3，还有如下新的定位方法：

问题3如图3，在△ABC中，I1,I2,I3分别为顶点A,B,C所对的旁心；点M1,M2,M3分别为边BC,CA,AB的中点，且直线M2M3分别与I1I2,I1I3交于点V1,U1，直线M3M1分别与I2I3,I2I1交于点V2,U2，直线M1M2分别与I3I1,I3I2交于点V3,U3. 求证:U1,U2,U3,V1,V2,V3六点共圆.

图3

下面说明这两种定位的方法是一致. 如图4，我们的想法是，先由问题1的方法产U1,V1;U2,V2;U3,V3，即假设I1B∩A1B1=U1，I1C∩A1C1=V1.U2,V2;U3,V3类似得到. 由问题1的引申结论(3)可知，U1V1∥BC，并且直线U1V1平分边AB,AC，也就是说直线U1V1通过边AB,AC的中点M3,M2；类似的直线U2V2通过边BA,BC的中点M3,M1；直线U3V3通过边CA,CB的中点M2,M1. 为了说明两种定位方法一致，只须证明A3,U1,V2,B3四点共线就行了. 因为U1V1∥BC，所以

∠BU1M3=∠M3BU1，从而M3B=M3U1. 同理，M3A=M3V2. 于是

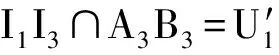
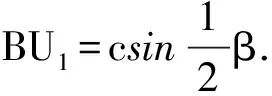
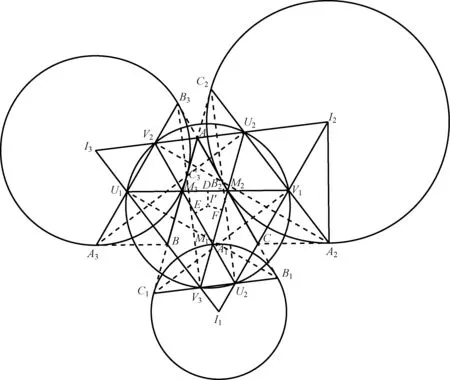
图4

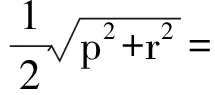
由上面的计算分析，我们还可以得到一些有趣的结论:

(5)四点组A,B,U1,V2；B,C,U2,V3；C,A,U3,V1都四点共圆；

(6)U1V1=U2V2=U3V3=p；

(7)△U1U2U3≅△V1V2V3；

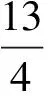
其中(5)、(6)由上述分析过程显然成立，而(7)、(8)需要一番计算分析，留给有兴趣的读者进一步讨论.

问题3中的结论其实就是有趣的Conway圆[3]:

问题4(Conway圆) 如图5，在△ABC中，边CA,BA分别延长至A1,A2，使得AA1=AA2=BC=a；边CB,AB分别延长至B1,B2，使得BB1=BB2=CA=b；边BC,AC分别延长至C1,C2，使得CC1=CC2=AB=c. 则有A1,A2,B1,B2,C1,C2六点共圆.

图5

由此可见，问题2或问题3中的旁心三角形上的六点圆其实就是中位三角形的Conway圆, 这样其实又找到了第三种定位U1,U2,U3,V1,V2,V3的方法. 笔者认为，这或许可以看作是问题1的出题背景. 由整体到局部，隐藏了很多关联信息，从而给解题者增加了解题障碍. 而解题者又可以通过由局部到整体的思想还原隐去的关联信息，从而找到解题思路. 因此，由整体到局部是一种重要的命题方法，而由局部到整体又是一种常用的解题策略.

3 问题联想

通过对原问题的探究分析，我们得到了两组有趣的六点共圆. 由此笔者又联想到了2008年第49届IMO试题第一题[2]：

问题5已知H是锐角△ABC的垂心，以边BC的中点为圆心，过H的圆与BC交于两点A1,A2；以边CA的中点为圆心，过H的圆与CA交于两点B1,B2；以边AB的中点为圆心，过H的圆与AB交于两点C1,C2. 证明: 六点A1,A2,B1,B2,C1,C2共圆.

问题5的证明及形变探究不妨留给读者思考. 形变探究，推陈出新，是一种重要的命题思路，遇到好的问题，我们不妨试着形变探索，或许会有很多惊喜和意外发现，甚至可以得到连命题者也意想不到的漂亮结果.