教会学生思考比教给学生方法更重要
黄桂君
(江苏省高邮中学 225600)
读了贵刊2016年第6期《函数结构任繁杂 巧妙转化变通达》一文,很有收益,雷波老师善于将函数表达式通过巧妙的转化,使得复杂的问题得以化解从而轻松解决.
也很受启发:教给学生解题方法当然重要,然而更重要的是教会学生思考,即探寻从无到有或从有到优的思路,并能帮助学生理解数学本质.
关于原问题与转化的关系,笔者以为应该首先着力研究原始问题,遇到困难时,再考虑转化.
1 关于2015年新课标全国卷Ⅰ文科第21题
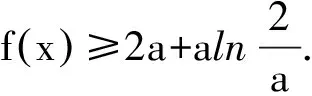
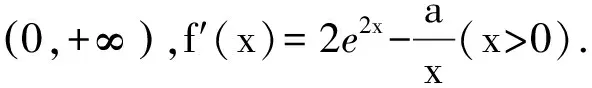

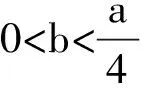
尽管可通过转化另解,如雷老师将其转化为两个比较简单的函数(法2),最好其中有一个是常数函数(法3)的图像交点问题,回避了寻找自变量b使f′(b)<0的“难点”,但上述对原始问题的探寻、思考对学生来说还是很重要的.从简单开始思考,就显得自然(许多时候我们由于思维定势往往把问题想复杂了).
无独有偶,2016年还是新课标全国卷Ⅰ,第21题文(2)、理(1)都是同一个类似问题:已知函数f(x)=(x-2)ex+a(x-1)2有两个零点,求a的取值范围.
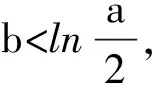
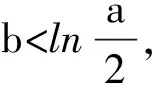
实际情况是这似乎是一个难点.在寻找函数的一个自变量b,使f(b)>0时,学生习惯具体数据,不习惯抽象的字母;习惯答案就是一个,不习惯灵活的探寻(多了反而找不到).这往往能反映出一个学生的数学学科素养,所以成为高考考查的重点.
如,2013年江苏高考第20题一片段:试求函数f(x)=lnx-ax(a<0)零点的个数,并证明你的结论.很多考生通过转化,简单的说因为函数y=lnx与y=ax(a<0)的图像只有一个交点,所以函数f(x)=lnx-ax(a<0)有一个零点(受平时老师教给方法的影响).这不能算作证明,也不知道怎么用数学语言表达(推理),所以被扣了分喊冤.
而应该根据函数零点存在性定理论证:因为f(1)=-a>0,f(ea)=a-aea=a(1-ea)<0,且函数f(x)图像在[ea,1]上不间断, 所以f(x)在(ea,1)上存在零点.

2016年江苏高考第19题同样对此进行了重复考查:“g(loga2)=aloga2+bloga2-2>aloga2-2=0”,同前面考生不会尝试选取“ea”一样,还是有很多考生不习惯选取诸如“loga2”等自变量进行探索.
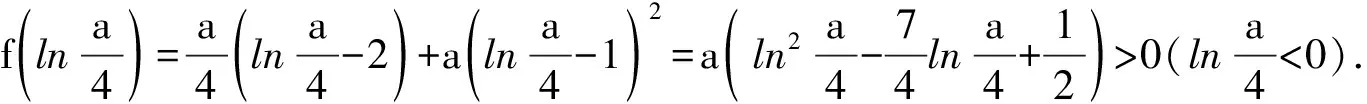
抛弃思维定势围绕核心又结合实际的做法,谁说不也是一种创新呢?
对于(2):雷老师由于受到文章论点的限制,没有解析,只是说“只要突破了第(1)问,第(2)问则迎刃而解”.其实并非如此,通过如下透视同样能说明思想比方法更重要.
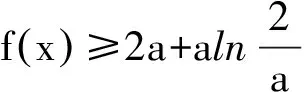

问题1求函数f(x)=ex(2x-1)-x的单调区间.(f′(x)=ex(2x+1)-1有一个零点x0=0)

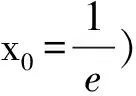
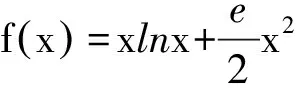
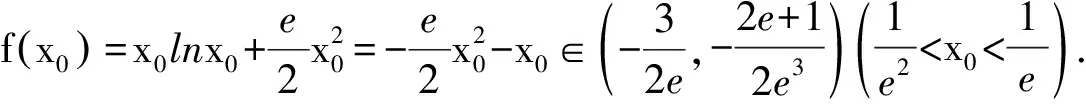
问题3下面的证明过程中有问题吗?(投影一道试题局部学生的书面表达)
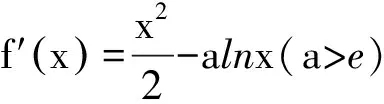

上述推理是不严谨的,特别是a取e2得g(e2)>0更是不可靠的.教学中甚至有许多数学优秀的学生觉得结论明显,没有必要找自变量验证!我就提出了一个问题:如果函数f(x)在区间(-∞,1)上单调递减,在(1,+∞)上递增,图像连续不间断,且f(1)<0,那么函数f(x)有几个零点?为什么?动手画图试试看,如f(x)在(1,+∞)上递增且穿过x轴,或不穿过x轴而以它为渐近线等.让他们懂得:重结果,也要重过程.讲推理,更要说道理.
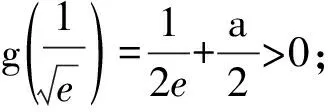
问题4记问题3中两个零点为x1,x2,再设问:如证明x1x2>e.(改编的,过程略)
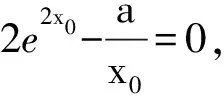
同样无独有偶,2016年新课标全国卷Ⅰ理科第21题(2)恰恰考的就是这样的问题:“设x1,x2是f(x)的两个零点,证明:x1+x2<2”.(过程略)
2 关于原文例2

我有个疑问:“务必实施分离”的道理是什么?要淡化技能技巧,重视通性通法(基本方法).其实可以从下面几个出发点引导学生去思考(说一点实施分离的缘由):
常规思路1:即证明f(x)min>1,但是有困难,因为遇到了
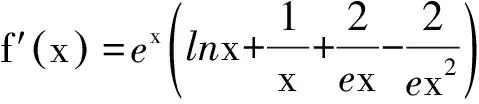



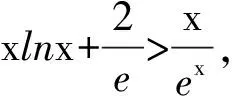
至此可以感觉到,如果对于2015年新课标全国卷Ⅰ的导数解答题在训练中过于强调转化等方法,没有让学生练习思考到位,那么对2016年的类似问题有可能还是做不好,考不出.
教学中我们既要教给学生一些方法,更要注重教会学生思考,让学生思考探究一些他们的能力能够“够得着”的问题,培养学生的数学学科素养.

