一个教学片段引发对纠错教学的思考*

花 奎 童旗军

(江苏省仪征中学 211900)

近日，在学校的“抽签听课”(事先不通知授课教师，电脑随机抽取教师课堂听课，便于了解真实的课堂)的活动中.笔者听了一节高一数学课，教师对一道习题进行了纠错教学.课后，笔者对师生进行了访谈交流，并对学生进行了检测分析，引发了笔者对数学纠错教学的思考.

1 教学实录片段

教者出示题目(这是学生作业中一道习题，课前教师进行纠错教学)：已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)图象上的一段(如图1所示)，那么在区间(0,2π)上，使等式f(x)=f(0)成立的x的取值集合为.

图1

所以f(x)=sin(2x+φ)，

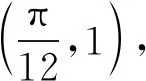
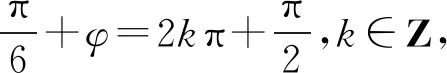
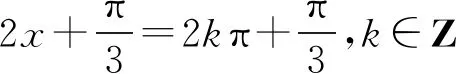
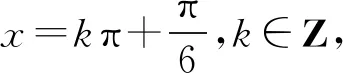
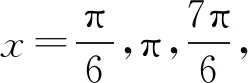
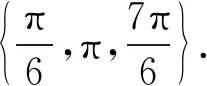
师：做的很好！本题就是由最值确定振幅A，周期确定ω，代入特殊值确定φ，要注意的是一定要代入最大值点或者最小值点，然后根据三角函数值求出角.

然后，教者开始讲授其他新课内容了.(听课中发现部分学生面露困惑之色.)

2 课后调测反馈分析

这次讲评，看似教会了学生这道题解法，也让学生展示，暴露了学生的“思维”，其实只是让学生展示了答案，教师只是强调了注意点.笔者认为这道题的纠错教学是不成功的，只唯正确答案为目标.教者对这道习题的研究不透，没有揭示本质.这道习题为什么要讲，学生的错误有哪些？通过讲评，是否实现了本题的纠错教学的目的？为此，笔者分别对教者和学生进行了访谈交流，并设计了两道测试题对学生进行了检测，以观察纠错教学之效果.

2.1 课后与教者的访谈交流

笔者：您为什么讲评这道习题？

教者：因为错误率比较高，全班大概有30%的学生出错.

笔者：学生主要错在哪里呢？

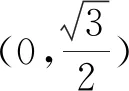
笔者：您认为本题教学目的实现了吗？

教者：学生的展示很完整，我也进行了强调，而且前面上课也强调好几次了，应该没有问题了.

2.2 课后与部分学生的访谈交流

笔者：对于这道习题，你们听懂了吗？现在再做类似的题，会不会出错呢？

学生(众)：听懂了.类似的题应该不会出错了.

笔者：你们之前做错了，错在哪里呢？

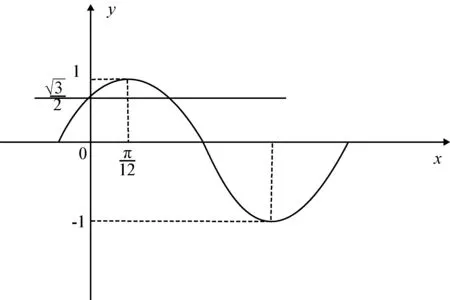
图2

笔者：你们现在还有什么困惑呢？

学生的错误和困惑就是纠错教学的关键.师者传道授业解惑也，这道题纠错教学如此草草，传道了吗？解惑了吗？揭示问题的本质了吗？

2.3 测试情况及统计分析

正如教者所说，类似的习题没有问题了吗？如果给出的问题中函数图象上不能找到最大值点或最小值点，学生还能解决吗？如果f(0)不是特殊角的三角函数的值，学生还会求x的值吗？为此，设计了两个问题来检测学生课堂学习的掌握情况，问题如下：

(1)如图3是函数f(x)=Asin(ωx+φ)(A>0,0<ω<3，0<φ<π)图象的一部分，试写出此函数f(x)的解析式.

图3

通过检测并统计分析发现，学生处理的非常不好.

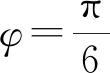
由此说明，通过本次纠错教学，学生并没有真正领悟到根据三角函数图象求解析式及根据三角函数值求角的通解通法之本质，从而不能灵活地运用.

3 对数学纠错教学的思考

3.1 纠错不应当简单告诉正确答案

3.2 开展微型探究揭示问题的本质

从个体对问题解决感受、体验的角度，我们可以将学生的错误原因分为两类：(1)我为什么不可以这样想?这类问题纠错主要帮助学生对解题策略的理性选择.(2)我这样想错在哪里?这类问题纠错主要帮助学生梳理相关概念的联系和区别.为了帮助学生解决这两个问题，可以设计问题串引导学生开展微型探究.以本文中的纠错教学为例，可以设计如下一个探究过程.

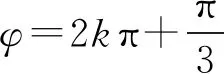
上述解法有错吗？如何去检验呢？为什么会出错呢？

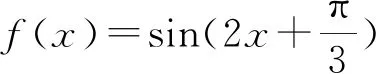
师：很好！抓住了图象的关键特性，看来可以通过画图检验，去伪存真.为什么会出现增解的呢？

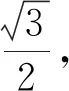
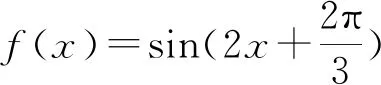
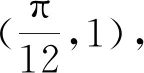
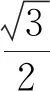
通过上述问题驱动学生进行微型探究，帮助学生弄清了错在哪里及如何解决问题.建议数学纠错课堂教学尽可能以What， How,Why等问题驱动微型探究，揭示数学本质.

3.3 适当变式 完善认知结构

纠错教学不仅帮助学生发现错误寻找错因得到正解，还要弄清学生的想法及其蕴含的道理，挖掘本原.也就是要弄清学生原始的朴素的想法，来自哪里？就是让学生错误的隐性知识或隐性认知模式伴随师生共同探究和反思过程“显现”出来，并通过自身的内在修正，明晓其中之道，完善其自身的认知结构.如本文中的纠错教学中，可以设计如下一个变式探究的过程.

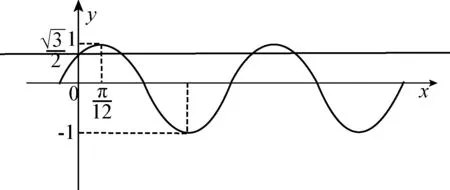
图4

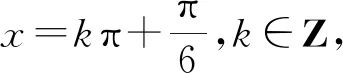
通过问题探究和变式训练发现这类问题中所蕴含的数学概念、方法或思想的本质属性，在知识迁移上达到重组水平，这也是我们经常说的“融会贯通”.通过学生E的解法展示和修正，师生自然会有这样的问题：这种解法的道理是什么？这就需要我们设计问题挖掘本原来回答学生的困惑，发现其中的道理，有了知其然，更要知其所以然的深刻认识.

“错解”在教学的过程中是不可避免的，教师在纠错教学过程中应该引导学生通过微型探究发现与分析错解原因，揭示本质，还要以学生的解法和困惑为资源，适度变式引申，帮助学生达到认识错误，完善其自身的认知结构，提高理解水平.