以兴安盟为例的布病传播及风险分析
杨新爱, 邓明明
(1. 山西工程职业技术学院 计算机工程系, 山西 太原030009;2. 中北大学 经济管理学院, 山西 太原 030051)
以兴安盟为例的布病传播及风险分析
杨新爱1, 邓明明2
(1. 山西工程职业技术学院 计算机工程系, 山西 太原030009;2. 中北大学 经济管理学院, 山西 太原 030051)
针对兴安盟地区人间病例呈周期性, 且各斑块间存在羊群调运和细菌传播的现象, 建立了一类周期斑块动力学模型. 对模型进行了理论分析, 包括基本再生数以及无病周期解的稳定性; 通过对人间病例的数据拟合, 反推出羊群布病阳性率; 结合ArcGIS给出布病风险分布图, 对防控措施进行了评估. 结果表明: 提高免疫覆盖率、 控制旗县间的羊群调运可有效抑制布病传播.
布病; 动力学模型; 周期性; 羊群调运; ArcGIS
布病在我国50年代开始流行和高发, 之后开始下降. 然而, 随着我国畜牧业的发展, 自20世纪90年代起, 布病人间发病病例数呈现增长的趋势, 尤其是21世纪, 布病发病数呈现指数增长[1]. 布病作为人畜共患病, 目前主要在我国畜牧业发达的几个区域流行, 主要传播以羊群布病为主, 人间布病主要由患病的羊群传染, 环境中的布鲁氏菌也是易感人群的另一种传播方式. 布病的传播严重危害人民的正常生活和生产发展, 需要找到根除或控制布病的措施.
布病的研究已有很多工作. 其中, 统计学者运用统计方法建立统计学模型, 得到一些结果[2-3]. 近年来, 侯强、 李明涛等[4-8]通过对内蒙古进行实地考察, 结合实际数据研究了牛羊公用牧场的混合交叉传染布病模型, 人群-羊群交叉传染布病模型, 以及分阶段的羊群布病传播模型. 这些研究都为布病的防控提供了理论依据, 但在动物疫病的防控过程中, 不同区域的羊群调运和细菌传播也增大了布病传播的风险. 因此, 针对斑块之间的风险因素, 研究布病的流行规律、 防控措施, 以及对防控措施进行风险评估, 也是一项迫在眉睫的任务.
兴安盟人间病例呈周期性, 且地理位置上呈自东向西传播规律. 为探索兴安盟地区布病在各斑块的传播规律, 并有效控制布病的流行, 本文建立了带周期的斑块布病动力学模型, 对模型进行动力学分析和数值模拟, 并结合ArcGIS给出了兴安盟羊群布病阳性率等级分布图.
1 动力学模型的建立
兴安盟人间布病主要由患布病的羊群传染, 而环境中的布鲁氏菌也可以传染易感人群. 因此, 模型所考虑的种群包括羊群(N)、 人群(N1)、 环境中的细菌(W). 将羊群(N)分为四个状态: 易感者状态S, 病菌携带者状态I, 病菌阳性状态C和免疫状态R, 将人群(N1)分为三个状态: 易感状态U, 患病急性状态V, 患病慢性状态D.

图 1 布病感染流程图Fig.1 Transmission diagram on the dynamical transmission of brucellosis
将兴安盟地区按县界线划分, 布病在羊群、 人群之间, 六个旗县之间的传播流程图见图 1. 由流程图(图1), 建立如下周期斑块动力学模型(1), 所涉及的变量和参数意义见表 1. 其中,Ai(t),ki(t),di(t),pi(t),δi(t)均为周期函数.





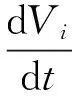
其中,

表 1 模型(1)中有关参数的说明Tab.1 Description of parameters in model (1)
2 模型的动力学分析
因为周期斑块动力学模型(1)中的前5个方程独立, 只需通过前5个方程(系统(3))来研究模型(1)的动力学性态.




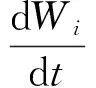
引理1 系统(3)的正向不变集为

证明首先, 引入两个记号. 假设g(t)是一个周期为ω的周期函数
将系统(3)的前4个方程相加, 可得
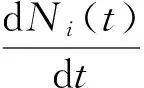
因此,
进而,
证毕.
2.1 基本再生数
疾病的基本再生数是疾病最主要的特征量之一, 用文献[10]的方法计算周期流行病的基本再生数. 首先, 令系统(3)右边为0, 且Ii=Ci=Ri=Wi=0, 得

将式(4)展开为
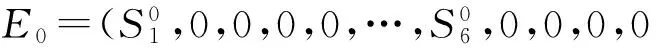
再利用文献[10]方法, 计算系统(3)的基本再生数.
现只需考虑Ii,Ci,Wi, 在无病平衡点处分别对Ii,Ci,Wi求偏导, 得
其中,
考虑系统
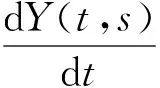
当t≥s,Y(s,s)=I,
其中,I为3×3单位矩阵.

于是, 周期系统(3)的基本再生数为
R0=ρ(L).
2.2 无病周期解的全局稳定性
由辅助系统和比较定理[9], 证明系统无病周期解E0的全局稳定性.
首先, 考虑辅助系统

其雅可比矩阵为

定理1 当R0<1时, 无病周期解E0在Γ内是全局渐近稳定的.
证明只需证明E0的全局吸引性.
当R0<1, 可得[11]ρ(ΦF-V(ω))<1, 对于充分小的ε,ρ(ΦF-V+M(ω))<1, 其中

显然,

1≤i≤n.
因为辅助系统(5)的正平衡点S0全局稳定. 则得, 对于ε, 存在T, 使得t>T时,S(t)≤S0+ε, 其中,S(t)=(S1(t),S2(t),S3(t),S4(t),S5(t),S6(t)). 于是, 可得如下系统
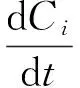
1≤i≤6,
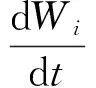

利用比较定理[9], 可得
((Ii(t),Ci(t),Wi(t))→(0,0,0),t→∞,
i=1,2,…,6.
再利用渐近自治系统理论[12], 可得
((Si(t),Ii(t),Ci(t),Ri(t),Wi(t))→
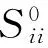
所以, 当R0<1时, 无病周期解E0是全局吸引的. 因此, 当R0<1时, 系统(3)的无病周期解全局渐近稳定.
证毕.
3 模型的合理性验证
图 2 为兴安盟地区各旗县人间布病发病数据与动力学模型(1)的拟合曲线图. 由图2可知: 扎赉特旗、 前旗和乌兰浩特地区的数据拟合结果较好. 由图2(a) 和图2(b)可以看出, 12月份扎赉特旗和科尔沁右翼前旗的数据点比其它月份都高; 由图2(d),图2(e)和图2(f)可以看出, 科尔沁右翼中旗发病数在2011年第3季度明显突增, 随后一个月突然降低, 突泉县和阿尔山市也出现同样的现象, 且无较好周期现象, 具体原因尚且不明, 可将这些特殊的数据点视为奇异点. 综上, 说明模型(1)具有一定的合理性, 可以利用模型(1)来预测疾病流行趋势, 并对疾病防控措施进行评估.
另外, 可以从拟合结果反推出的模型(1)参数值. 进而结合布病在人间的发病数据, 来反推兴安盟各旗县的羊群布病阳性数据, 见图3. 同时, 为了结果更加直观明显, 本文应用ARCGIS软件绘出了羊群布病阳性率分布图, 见图4. 由图3和图4可得, 2011年和2012年兴安盟六个旗县羊群布病的阳性率. 2011年阳性率由高到底依次为: 前旗(约8%)、 扎赉特旗(约7%)、 乌兰浩特市(约7%)、 突泉县(约5%)、 中旗(约4%), 阿尔山(1.2%). 对比2012年, 羊群阳性率下降最快和最慢的分别为前旗和乌兰浩特.
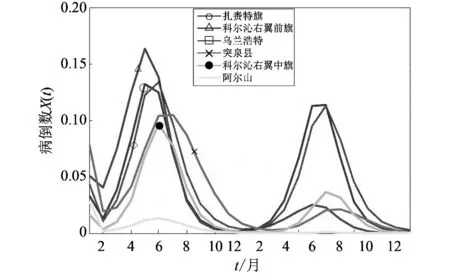
图 3 2011~2012兴安盟各旗县的羊群实际阳性率时间序列图Fig.3 The actual positive rate of sheep brucellosis in six counties from 2011 to 2012

图 4 2011~2012兴安盟各旗县羊群阳性率GIS分布图Fig.4 The GIS distribution graph about actual positive rate of sheep brucellosis from 2011 to 2012
4 风险分析
据调查所知, 兴安盟各旗县之间存在羊群的调运, 羊群调运究竟会给布鲁病的传播带来何种影响, 由于调运数据的缺失, 为了探讨这一问题, 这里仅从理论上做相关分析. 在保持其他参数不变的前提下, 假设兴安盟地区除扎赉特旗的其余五个旗县都为健康羊群, 仅扎赉特旗有3只携带布病细菌的羊. 由图5(a)发现, 目前的免疫覆盖率为40%, 5年内, 布病仅在阿尔山未流行. 综上可知, 布病流行初期, 布病的传播与斑块间的羊群调运有不可分离的关系. 由图5(b)知, 若将免疫覆盖率增加为90%, 布病在10年内仅在初期发病斑块内流行. 换句话说, 将免疫覆盖率力度提高到现在的90%, 便可以为无病区域的安全提供保障.
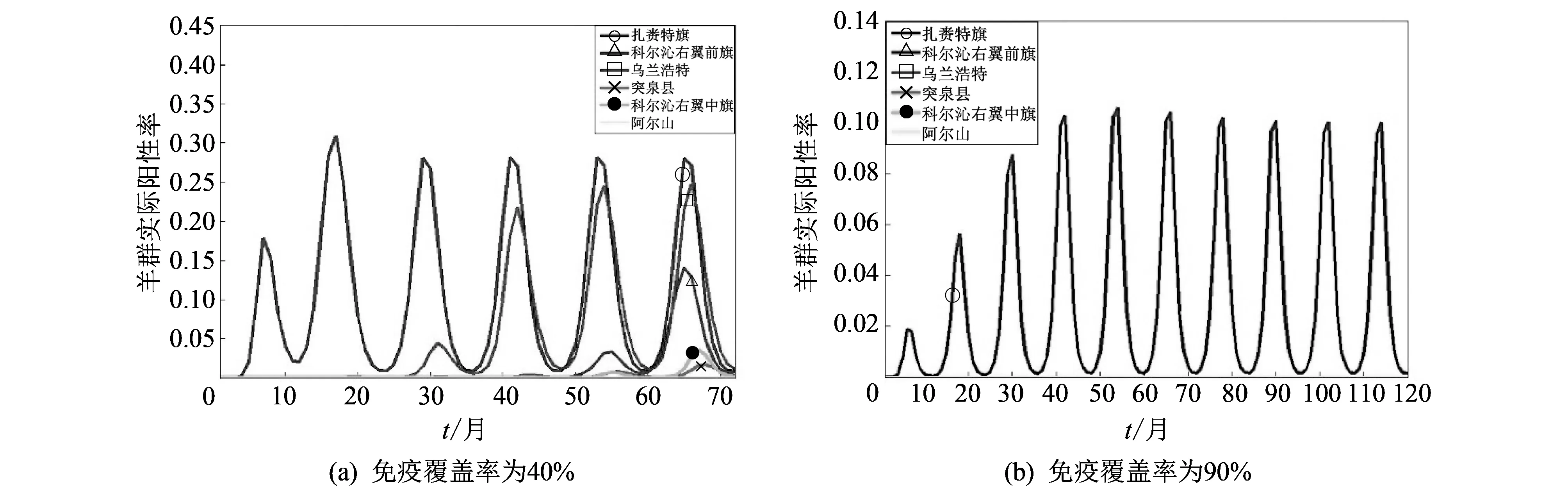
图 5 存在羊群调运时, 不同免疫覆盖率下各旗县的羊群布病阳性率时间序列图Fig.5 The time evolution about positive rate of sheep brucellosis under sheep movement with the different coverage rate of immunity
根据兴安盟羊群调运的实际背景, 绘制图 3 各旗县羊群存在调运时的羊群布病阳性率变化曲线图. 为探讨控制调运是否会对布病传播的控制起作用, 绘制了图6 各旗县控制羊群调运时的羊群布病阳性率变化曲线图. 对比图3和图6, 可以发现: 当布病在各旗县均已流行时, 控制调运对控制布病传播没有作用.
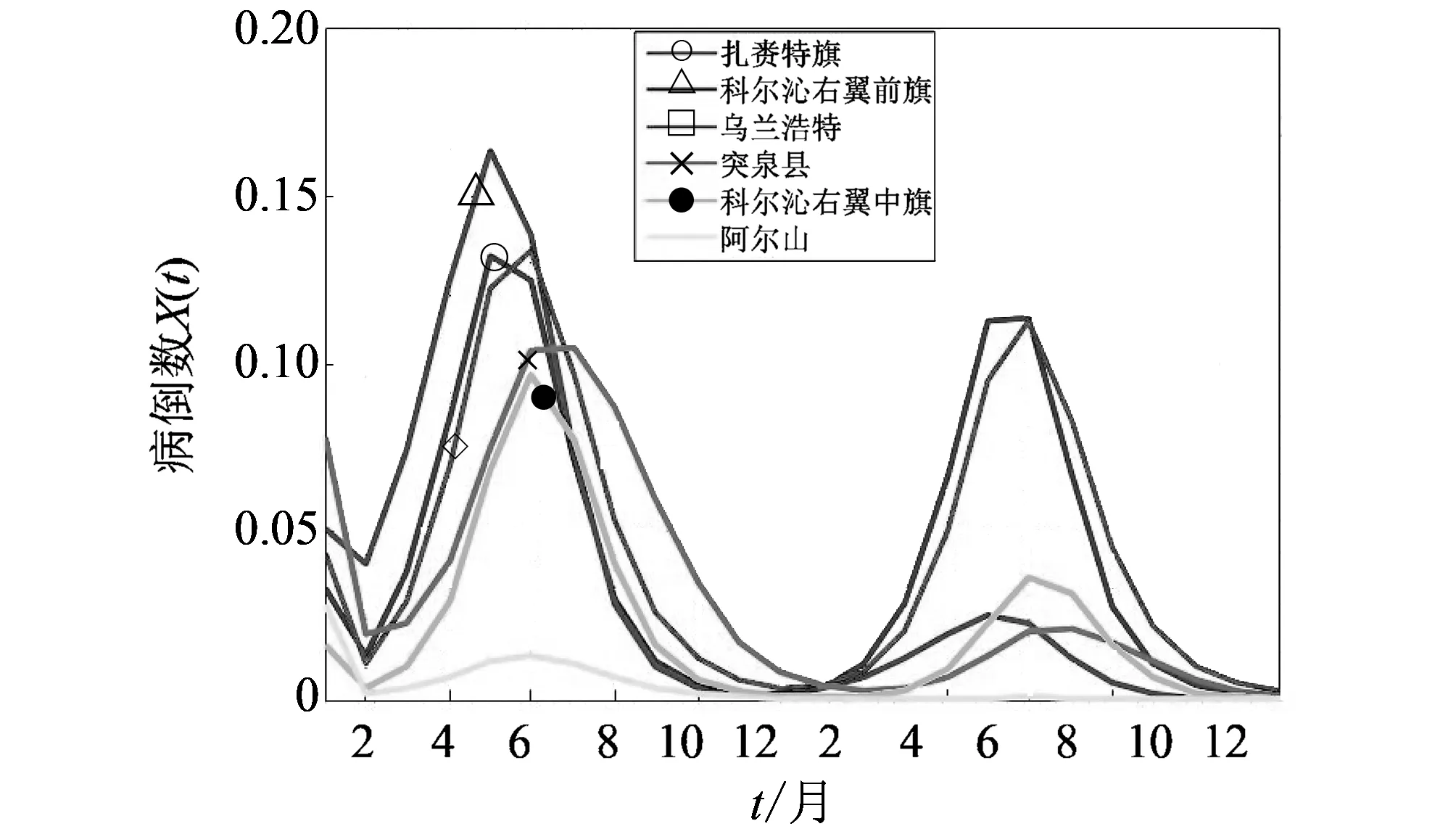
图 6 控制羊群调运时, 2011~2012兴安盟各旗县的羊群布病阳性率时间序列图Fig.6 The positive rate of sheep brucellosis in six counties from 2011 to 2012, when control the movement of sheep
5 结 论
本文建立了周期斑块布病动力学模型, 模型考虑了出生、 出栏、 免疫、 排菌、 检测的周期性以及各旗县间的调运, 并运用实际数据对模型进行拟合, 实际数据与模型解的拟合结果较好. 另外, 利用模型和兴安盟六个旗县人间布病新发病例数据, 反推出各旗县羊群的实际阳性率. 进一步结合ArcGIS给出兴安盟羊群布病等级分布图, 对防控措施进行评估, 可知: 提高免疫覆盖率有利于布病的防控; 在布病传播初期, 控制旗县之间的羊群调运可有效控制布病传播, 当布病已在各旗县均已流行时, 再控制调运不会对控制布病起作用.
[1] Pappas G, Papadimitriou P. Challenges in Brucella bacteraemia[J]. Int. J. Antimicrob Agents, 2007, 30(S1): 29-31.
[2] 吕爱军, 李槿年, 余为一.布鲁氏菌病感染预测模型的建立与精度比[J].中国动物检疫, 2000, 17(10): 21-22.
Lu Aijun, Li Jinnian, Yu Weiyi. Establishment of Brucellosis infection rate forcasting models and their accuracy comparison[J].China Animal Health Inspection, 2000, 17(10): 21-22. (in Chinese)
[3] 李仲来, 吕景生, 赵永利, 等.数学模型在全国布鲁氏菌病监测点疫情预测的应用[J].中国地方病防治杂志, 2000, 15(5): 273-275.
Li Zhonglai, Lu Jingsheng, Zhao Yongli, et al. Application of mathematical models to forecast for inspection district of Brucellosis in China[J]. Chinese Journal of Control of Endemic Disenaces, 2000, 15(5): 273-275. (in Chinese)
[4] Hou Qiang, Sun Xiangdong, Zhang Juan, et al. Modeling the transmission dynamics of sheep brucellosis in Inner Mongolia Autonomous Region, China[J]. Mathematical Biosciences, 2013, 242(1): 51-58.
[5] Li Mingtao, Sun Guiquan, Jin Zhen, et al. Transmission dynamics of a multi-group brucellosis model with mixed cross infection in public farm[J]. Applied Mathematics and Computation, 2014, 237(5): 582-594.
[6] Li Mingtao, Jin Zhen, Sun Guiquan, et al. Modeling direct and indirect disease transmission using multi-group model[J]. Journal of Mathematical Analysis and Applications. 2017, 446 (2): 1292-1309.
[7] Li Mingtao, Sun Guiquan, Zhang Wenyi, et al. Model-based evaluation of strategies to control brucellosis in China[J]. International journal of environmental research and public health. 2017, 14(3), 295.
[8] Li Mingtao, Sun Guiquan, Zhang Juan, et al. Transmission dynamics and control for a Brucellosis Model in Hinggan League of Inner Mongolia[J]. China. Mathematical Bioscience and Engineering, 2014, 11 (5): 1115-1137.
[9] Li Li. Monthly periodic outbreak of hemorrhagic fever with renal syndrome in China[J]. Journal of Biological Systems, 2016, 24(4): 519-533.
[10] Wang Wendi, Zhao Xiaoqiang. Threshold dynamics for compartmental epidemic models in periodic environments[J]. Dynam Differential Equations, 2008, 20(3): 699-717.
[11] Zhang Fang, Zhao Xiaoqiang. A periodic epidemic model in a patchy environment [J]. J Math Anal Appl, 2007, 325: 496-516.
[12] Thieme H R. Convergence results and a Poincar′e-Bendixson trichotomy for asymptotically automous differential equations[J]. Journal Mathematical Biology, 1992(30): 755-763.
TheSpreadandRiskAnalysisofBrucellosisTakingHingganLeagueasanExample
YANG Xin-ai1, DENG Ming-ming2
(1. Dept. of Computer Engineering, Shanxi Engineering Vocational College, Taiyuan 030009, China;2. School of Economics and Management, North University of China, Taiyuan 030051, China)
Brucellosis in Hinggan League presents characteristics of seasonal human cases and sheep migration, bacteria diffusion between regions. Based on this, a periodic sub-regional paths dynamic spreading model was established. Dynamic characteristic of the model was analyzed, it include the solution of transmission threshold and the proof about global stability of the disease-free periodic solution. Besides, the rationality of the model was confirmed by data fitting about human cases, the positive rate of sheep brucellosis was simultaneously obtained. Finally, with the help of geographic information system (ArcGIS), risk charts of Hinggan League sheep brucellosis were shown, and precaution and control measures were assessed. The simulation results illustrate that increasing the immunization coverage rate and controlling the sheep transportation between plaques can effectively restrain brucellosis spread.
Brucellosis; dynamical model; periodicity; sheep migration; geographic information system (ArcGIS)
1673-3193(2017)05-0536-08
2017-06-11
山西省软科学基金项目(2017041016-1)
杨新爱(1963-), 女, 副教授, 硕士, 主要从事计算机应用的教学与研究.
O175
A
10.3969/j.issn.1673-3193.2017.05.006

