能量梯级利用型温差发电系统的动态特性研究

许昊煜

(中国大唐集团科学技术研究院有限公司华东分公司， 安徽 合肥 230011)

能量梯级利用型温差发电系统的动态特性研究

许昊煜

(中国大唐集团科学技术研究院有限公司华东分公司， 安徽 合肥 230011)

为了增强对温差发电系统的动态特性的认识， 提高系统级发电效率， 从而拓展温差发电技术在分布式能源以及耦合常规热源发电方面的应用前景， 针对一种能量梯级利用型温差发电系统进行数学建模及仿真计算， 并据此搭建了实验台. 实验与仿真计算的结果证明， 温差发电系统的数学模型能够较好地反映系统的动态性能， 且合理地布置高、 中、 低温温差发电模块能够有效地实现对热源的梯级利用， 系统级发电功率及发电效率可分别达到393.33 W和7.05%.

温差发电； 梯级利用； 数学建模； 动态特性

温差发电技术作为一种全固态热电转化方式， 具有体积小、 结构简单、 无运动部件且输出稳定等优点， 因此可以结合废余热、 太阳能或天然气燃烧产生的热源进行发电[1-2]， 在分布式能源方面也具有较好的应用前景. 尽管如此， 相较于传统的发电方式， 温差发电系统的系统效率较低[3-4]， 且由于缺乏可以较为准确地描述其动态特性的仿真模型， 因此温差发电技术的性能预测及系统优化的相关研究也受到了一定的制约.

虽然有相关研究在提高热电材料及温差发电系统性能方面均取得了一些成果[5-8]， 但其中大多围绕单级温差发电系统进行， 对于高、 中、 低温耦合的温差发电系统的动态性能的研究甚少[3]. 因此， 本文着眼于耦合高、 中低温热源， 提出一种能量梯级利用型温差发电系统， 构建该系统的仿真模型， 并结合实验的手段分析系统的动态特性.

1 温差发电系统基本原理

1.1 梯级利用型温差发电系统介绍

温差发电是指当金属、 半导体以及一些纳米材料受热时， 其中的电子(空穴)顺温度梯度迁移从而产生电能的技术[9]. 单个温差发电模块的发电量大小主要取决于模块冷热端的温差， 而在高温热源供热的系统中， 通过耦合高、 中低温温差发电模块， 并通过合理的布置， 使其工作在相应的最佳温度区间， 可以提高温差发电系统的整体效率， 从而形成对于热源的能量梯级利用[10]. 基于以上的背景， 本文构建了一个能量梯级利用型温差发电系统的仿真模型， 通过数值计算和实验的方法对于该系统进行了研究.

梯级利用型温差发电系统的基本结构如图1所示. 主要包括： 燃烧系统(风机、 混合室和遮焰罩)、 温差发电模块(高、 中、 低温温差发电模块)、 散热套、 冷却水再热装置、 引风装置、 数据采集系统等子系统. 通过计算估计热源在系统中各处的温度， 确定高温温差发电模块采用PbSnTe型环形热电模块， 其最佳工作区间约为500～700 ℃[11]， 中温温差发电采用最佳工作温度区间在350 ℃(623.15 K)左右的Bi-Te半导体热电模块[12]， 低温温差发电模块选取工作温度区间在100 ℃以下的碲化铋温差发电模块[13].

1.2 系统基本工作原理

图 1 中， 虚线表示燃气以及高温烟气的走向， 与之对应的实线则表示了冷却水的走向. 在图中所示的混合室中， 燃气与空气按照规定比例进行强制预混并喷入遮焰罩燃烧， 火焰及高温烟气通过遮焰罩上的孔洞进入高温模块热端进行换热； 随后， 烟道中高温烟气一方面为中温温差发电模块提供热源， 另一方面与冷却水再热管中的冷却水进行换热； 最后通过引风装置排出系统.

冷却水流经高温温差发电模块冷端， 与模块热端进行热交换后， 通往冷却水再热器， 吸收烟道中高温烟气放出的热量， 温度进一步提高， 随后进入低温温差发电模块进行发电.

结合以上工作过程可知， 由预混器以及遮焰罩组成的燃烧系统提供了高温烟气， 其直接作为高温与中温温差发电模块的热源， 同时间接地为低温模块提供了热源(再热后的冷却水)， 体现了对系统热源热能的梯级利用.

图 1 能量梯级利用型温差发电系统的结构示意图Fig.1 Schematic diagram of cascade utilization TEG system

2 系统动态特性仿真

根据上文提出的系统设计思路， 构建反映整体系统动态特性的数学模型， 并用以预测系统的动态性能.

2.1 系统物理模型的构建

系统的模型主要分为两个方面， 一方面为烟道和管路组成的传热模型， 另一方面是以高、 中、 低温温差发电模块为主的输出功率性能计算模型.

图 2 显示了系统的整体结构模型图， 其中高温温差发电模块为环形模块， 中、 低温则为方形模块， 由热电材料、 电镀层、 陶瓷耐热层、 导电片以及焊锡层等材料构成夹层结构.

系统中高温模块的热端与燃烧产生的烟气进行对流和辐射方式传热； 中、 低温温差发电模块则分别与烟气和再热冷却水进行对流换热. 以高温温差发电模块为例， 构建各级的传热模型. 如图 3 所示， 高温烟气首先与高温热电模块进行对流换热以及辐射换热， 将环形模块离散为若干微元， 通过定义不同微元的物性参数， 模拟热量在不同材料夹层中传导的过程.

图 2 热能梯级利用型温差发电系统模型图Fig.2 Model of the cascade utilization TEG system

图 3 环形高温温差发电模块模型Fig.3 Model of annular high temperature thermoelectric module

高温模块冷端向冷却水中的传热为Qout_htem， 以此计算模块冷热端的温度差， 结合赛贝克系数求解出模块输出电压和功率. 由于高温温差发电模块呈现环形， 因此在简化为一维热传导模型时需要将每个微元的传热面积与当地半径联系起来. 使用类似的模型计算中、 低温温差发电模块的传热， 不同之处在于中、 低温模块为方块， 因此使用统一的截面积作为传热面积即可. 图中，r_out 为环形模块外壁处半径、Ar_out为环形模块外壁面积、r_in为环形模块外壁处半径、Ar_in为环形模块外壁面积、r为环形模块外壁任意位置的半径、Ar为环形模块外壁任意位置的半径处的截面积、 Q_fl1为环形模块内壁吸收热量、 P_htem为环形模块发出电能、Qout_htem为环形模块外壁释放热量.

除了各级模块与相应热源的传热以外， 系统中还涉及到一些能量损失， 例如烟道以及管路壁面对于环境的换热等， 如图 4 所示. 在高温烟气进入中温模块以及冷却水再热管前， 模型中添加了这一换热模型以计算热损失.

图 4 烟道与环境换热模型Fig.4 Model of heat exchange between flue and environment

2.2 数学模型的建立

本系统的动态数学模型基于如下的简化假设：

1) 甲烷与空气充分预混， 烟道出口处烟气中无甲烷残留；

2) 热电模块除赛贝克、 电导率以及帕尔贴等热电性能系数以外， 其余物性参数都设为常数；

3) 高温烟气和冷却水在管道流动过程中的能量损失， 仅考虑为对流换热损失；

4) 忽略模块计算中由于接触界面不平导致的接触热阻， 假设同一平面上的温度梯度为零， 采用一维导热模型进行处理[14].

建立一维非稳态的微分控制方程如下[15]

式中：ρ为密度；c为比热容；S为源项；x为当地所处的位置；A(x)为随长度变化的截面积. 若计算环形模块， 需要关联半径r与换热面积的关系， 表示为

综上， 可以构建如图 5 所示的非稳态导热的数学模型， 其中P点为当前的位置，W点以及E点分别代表该点左右相邻的控制体中心点， 其边界为w与e， 该边界处位置值为xe与xw， 对应的换热面积为A(xe),A(xw). 计算高温环形模块时， 边界散热面积与边界所处的半径值有关. 例如环形模块内外径分别为r_in以及r_out， 取参考半径为r0=(r_in+r_out)/2， 则当半径为r时， 当地换热面积可换算如下[16]

图 5 非稳态热传导模型Fig.5 Non-steady thermal conduction model

2.3 发电性能计算模型[12]

根据以上传热模型计算所得的热电模块冷热端的温度， 结合不同位置的赛贝克系数可以计算模块输出.

以高温温差发电模块为例， 在P型和N型半导体材料物性均一化的假设下， 赛贝克电动势

为发电模块匹配相应的负载RL， 可计算出高温模块发电功率

由此可得单级模块的发电效率

式中：Qhtem为高温温差发电模块的吸热量.

同理， 可以分别计算出中、 低温模块的赛贝克电动势Voc_mtem,Voc_ltem， 输出功率Pmetm,Pltem， 以及发电效率ηmtem,ηltem.

Is“ sensitive muscle nursing” the antidote for cosmeceuticals? 8 7

使用Matlab编制以上非稳态导热模型以及发电模块发电性能计算模型， 以燃烧产生的高温烟气温度随时间变化的测量值作为输入， 从而可以计算出高、 中、 低温热电模块的开路电压以及系统功率.

3 发电实验台的实验研究

3.1 实验装置介绍

根据前文的设计思路搭建了一种梯级利用型温差发电实验台， 如图 6 所示.

图 6 实验台三维系统图Fig.6 Three-dimensional diagram of the experimental testbed

燃气瓶、 风机与预混器通过管道相连， 燃气与升压后的空气按照1∶1.2的比例在混合器中预混. 其中燃气流量通过与气瓶连接的阀门控制， 空气的流量调节通过控制风机的功率实现. 预混好的气体随后被喷入燃烧器燃烧， 产生的高温烟气受到环形带孔遮焰装置的扰流， 透过孔洞进入高温模块热端完成换热后流向烟道； 随后， 烟道中的高温烟气一方面为中温温差发电模块提供热源， 另一方面冲刷冷却水再热管， 最后排出系统.

冷却水在冷却水套中为高温温差发电模块提供冷源， 与模块热端进行换热后通往冷却水再热器， 与烟道中的高温烟气进一步换热， 其温度继续升高； 随后进入低温温差发电模块作为热源. 在此系统中， 高、 中、 低温温差发电模块被布置于系统的不同温度区间， 并通过冷却水或空气冷却发电模块的冷端以产生电能， 从而实现热能的梯级利用.

3.2 实验和仿真结果对比及分析

为了考察本系统的动、 静态性能， 验证系统的动态特性仿真模型的合理性， 分别采集实验台启动过程以及燃料流量做扰动过程时的发电性能参数， 并与仿真计算结果进行对比.

3.2.1 系统启动过程中仿真与实验结果对比

固定燃气流量为0.16 m3/h， 冷却水流量为12.5 L/min， 测量高、 中、 低温温差发电模块的内阻， 并调整负载的阻值与各级模块的内阻一致， 从而测量最大输出功率下的各模块电压.

图 7 系统启动过程各模块开路电压的模拟与实验值Fig.7 Simulative and experimental value of open circuit voltages in different modules during system starting

图 7～图 8 分别显示了在启动过程中， 高、 中、 低温热电模块的开路电压以及系统功率的仿真值与实验值的对比.

图 8 系统启动过程系统输出功率的模拟与实验值Fig.8 Simulative and experimental value of system’s output power during system starting

随后通过标准差与平均相对误差衡量实验与仿真数据的重合度， 以下为各项指标试验值与仿真值的标准差表达式

式中：σ为标准差；N为实验值的总数；ti为当前的时刻；fs(ti),fe(ti)分别为当前时刻对应的对比项(电压或功率)的仿真值以及实验值.

为了更好地衡量实验值与仿真值之间的重合度， 引入平均相对误差

式中：lmax=(fs(ti)-fe(ti))max， 即仿真值与实验值的最大偏差. 高温温差发电模块开路电压的标准差为3.189 2 V， 其平均相对误差为9.12%， 中温温差发电开路电压的标准差为0.502 7 V， 其平均相对误差为5.11%， 低温温差发电开路电压的标准差为0.182 5 V， 其平均相对误差为3.09%. 由于平均相对误差揭示的是实验与仿真数据的绝对偏差量与最大偏差量之间的相对关系， 而高、 中低温模块电压的平均相对误差均未超过10%， 说明本模型在计算系统启动过程发电模块的动态特性方面较为可靠.

3.2.2 系统扰动过程中仿真与实验结果对比

图 9～图 10 显示了高、 中、 低温温差发电模块的开路电压以及系统功率在燃料侧作20%流量负向阶跃扰动后， 再作20%流量正向阶跃扰动时随时间变化的曲线图.

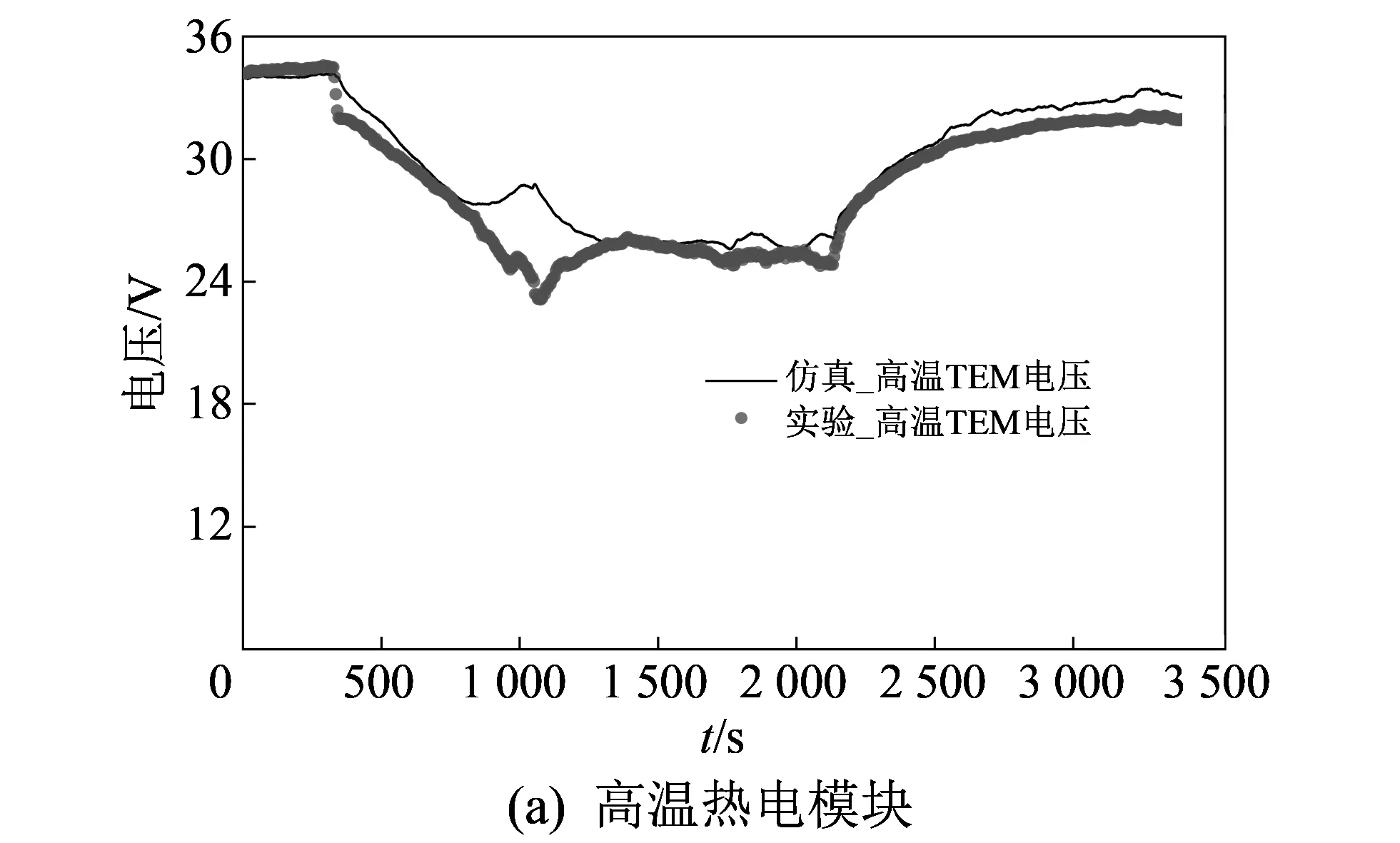
图 9 热源温度扰动时各热电模块开路电压的模拟与实验值Fig.9 Simulative and experimental value of open-circuit voltageswith temperature disturbance of heat source

通过标准差衡量实验与仿真数据的重合度， 高温温差发电开路电压的标准差为1.3 V， 中温温差发电开路电压的标准差为0.90 V， 低温温差发电开路电压的标准差为0.271 2 V. 图 10 所示的系统输出功率图中， 实验值与仿真值的标准差为29.51 W， 约占稳定功率的8.1%.

图 10 热源温度扰动时系统输出功率的模拟与实验值Fig.10 Simulative and experimental value of system’s output power with temperature disturbance of heat source

通过各级模块的开路电压计算出相应的输出特性参数， 将其统计在表 1 中. 对比各项参数的稳定时间以及稳定值， 可以看出高温模块的输出功率响应最快， 中温模块其次， 低温模块达到稳定所需时间最长. 系统各模块的输出功率在燃料流量作正向阶跃扰动时的稳定时间一般比其在燃料流量作负向阶跃扰动情况下的稳定时间短. 这是由于系统中的中、 低温热电模块等部件的使用了与空气的自然对流散热， 因此冷却能力较弱， 在燃料侧做流量负向阶跃扰动时， 各点温度更难达到稳定.

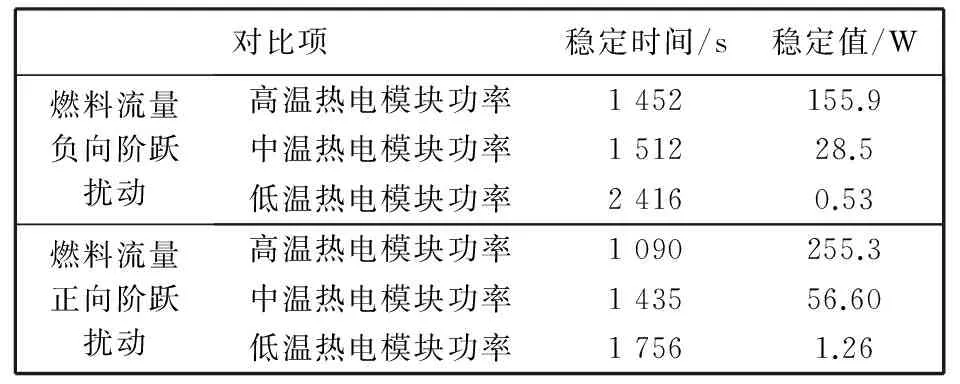
表 1 扰动过程中系统不同参数的动态特性Tab.1 Dynamic characteristics of different system parameters with the step disturbances

4 结 论

本文对于一种能量梯级利用型温差发电系统进行了数学建模与计算， 通过数值模拟和物理实验研究了系统的动态性能， 得出如下结论：

1) 本文所构建数学模型能较精确地反映整个系统在启动和扰动过程中的动态特性， 可以作为类似分析问题的工具；

2) 在燃料侧作流量正向阶跃扰动时， 系统的各项动态性能参数恢复稳定的时间更短， 在系统热源温度做斜坡下降扰动时， 达到稳定的时间更长. 这是由于系统的中、 低温热电模块等部件的冷端使用了自然对流散热， 因此冷却能力较弱， 在燃料侧做流量负向阶跃扰动时， 各点温度更难达到稳定；

3) 将高、 中、 低温温差发电模块合理地布置于一个以燃烧产生的高温烟气为热源的系统的不同温度区间中， 可以有效地对高温热源进行梯级利用. 在本文所提到的系统中， 系统级发电效率可以达到7.05%， 相较于单级高温温差发电实验台系统效率， 提升了1.93%， 增幅达到37.7%.

[1] Bell L E. Cooling, heating, generating power, and recovering waste heat with thermoelectric systems[J]. Science, 2008, 321(5895)： 1457.

[2] 赵建云, 朱冬生, 周泽广, 等. 温差发电技术的研究进展及现状[J]. 电源技术, 2010, 34(3)： 310-313.

Zhao Jianyun, Zhu Dongsheng, Zhou Zeguang, et al. Research progress of thermoelectric power generation[J]. Chinese Journal of Power Sources, 2010， 34(3)： 310-313. (in Chinese)

[3] 栾伟玲， 涂善东. 温差电技术的研究进展[J]. 科学通报， 2004， 49(11)： 1011-1019.

Luan Weiling， Xu Shandong. Study progress of the thermoelectric power generation[J]. Chinese Science Bulletin， 2004， 49(11)： 1011-1019. (in Chinese)

[4] Rowe D M. CRC handbook of thermoelectrics[M]. New York: CRC Press， 1995.

[5] 刘宏， 王继扬. 半导体热电材料研究进展[J]. 功能材料， 2000， 31(2)： 116-118.

Liu Hong， Wang Jiyang. Progress of semiconductor thermoelectric materials[J]. Journal of Functional Materials， 2000， 31(2)： 116-118. (in Chinese)

[6] 李红星， 赵新兵， 李伟文. 新型热电材料研究进展[J]. 材料导报， 2002， 16(6)： 20-23.

Li Hongxing， Zhao Xinbing， Li Weiwen. Recent development in new thermoelectric materials[J]. Materials Review， 2002， 16(6)： 20-23. (in Chinese)

[7] 鲍亮亮， 韩永辉， 张永忠， 等. 温差发电技术及工业余热温差发电系统设计研究[J]. 兵器材料科学与工程， 2015(2)： 110-114.

Bao Liangliang， Han Yonghui， Zhang Yongzhong， et al. Thermoelectric generation technology and design of thermoelectric generation system for industrial waste heat recovery[J]. Ordnance Material Science and Engineering， 2015(2)： 110-114. (in Chinese)

[8] 许昊煜. 多级热源利用型温差发电系统的流场与温度场优化设计[J]分布式能源， 2017， 2(1)： 44-49.

Xu Haoyu. Flow field and temperature field optimization study on the design of a multi-level heat source utilization thermoelectric generation system[J]Distributed Energy ， 2017， 2(1)： 44-49. (in Chinese)

[9] Gulian A M， Zharkov G F. Thermoelectric Phenomena[M]. Berlin: Springer， 2002.

[10] Hadjistassou C， Kyriakides E， Georgiou J. Designing high efficiency segmented thermoelectric generators[J]. Energy Conversion & Management， 2013， 66(66)： 165-172.

[11] Qiu K， Hayden A C S. Development of a thermoelectric self-powered residential heating system[J]. Journal of Power Sources， 2008， 180(2)： 884-889.

[12] 平会峰. 高温温差发电系统的性能分析[D]. 重庆： 重庆大学， 2015.

[13] Gou X， Xiao H， Yang S. Modeling， experimental study and optimization on low-temperature waste heat thermoelectric generator system[J]. Applied Energy， 2010， 87(10)： 3131-3136.

[14] Gou X， Ping H， Ou Q， et al. A novel thermoelectric generation system with thermal switch[J]. Energy Procedia， 2014(61)： 1713-1717.

[15] 陶文铨. 数值传热学[M]. 第2版. 西安： 西安交通大学出版社， 2001.

[16] Shen Z G， Wu S Y， Lan X. Theoretical analysis on the performance of annular thermoelectric couple[J]. Energy Conversion & Management， 2015， 89(89)： 244-250.

DynamicPerformanceStudyonaCascadingThermoelectricGenerationSystem

XU Hao-yu

(China Datang Corporation Science and Technology Research Institute Co., Ltd.East China Branch, Hefei 230011, China)

In order to obtain the dynamic characteristics and achieve higher generating efficiency of the thermoelectric generation(TEG) system so as to earn greater application prospect in distributed energy sources and the conventional energy supply, a cascading TEG system simulation model is built and analyzed, based on which, a test-bed is designed and built. The simulative and experimental results prove the correctness of the mathematical model and the rational arrangement of the high, medium and low temperature thermoelectric modules can make the cascading utilization of the heat source more effective. The output power and efficiency of the system increase to 393.33W and 7.05%.

thermoelectric generation; cascading utilization; mathematical model; dynamic characteristics

1673-3193(2017)05-0580-07

2017-05-05

许昊煜(1982-)， 男， 助理工程师， 硕士， 主要从事热力设备及系统节能、 优化和故障诊断的研究.

TM619

A

10.3969/j.issn.1673-3193.2017.05.013