变压器设计专家系统初始方案的决策方法研究

杜 江， 张烨烨， 王景芹， 岳 帅

(1. 河北工业大学 电磁场和电器可靠性省部共建重点实验室， 天津 300130；2. 首都航天机械公司， 北京 100071)

变压器设计专家系统初始方案的决策方法研究

杜 江1， 张烨烨1， 王景芹1， 岳 帅2

(1. 河北工业大学 电磁场和电器可靠性省部共建重点实验室， 天津 300130；2. 首都航天机械公司， 北京 100071)

针对现有变压器设计专家系统尚不能根据已有设计方案智能确定出最优初始方案的问题， 提出了一种基于加权灰靶理论确定最优初始方案的方法， 包含靶心度分析和贡献度分析. 在构建加权灰靶理论数学决策模型的基础上， 对10 kV级油浸式配电变压器设计专家系统初始方案的确定进行了实例演示， 并将演示结果与采用模糊理论方法得到的结果进行对比， 验证了基于加权灰靶理论确定最优初始方案的方法的可行性和优越性.

变压器； 专家系统； 加权灰靶理论

0 引 言

当前电力建设发展迅速， 变压器的市场广阔， 竞争激烈. 以节能降耗省材为目标的变压器优化设计越来越受到人们重视. 目前常用的变压器优化设计方法有正交试验法、 正多面体法、 循环遍历法等传统优化算法和粒子群算法、 人工鱼群算法、 遗传算法等智能仿生算法[1-2]， 这些算法均未涉及专家经验. 而变压器设计是一个复杂多变量非线性问题， 设计过程非常依赖于专家经验， 如何将优秀设计人员的丰富经验运用到设计中， 建立准确完善的设计方案， 是当前研究的热点. 在此背景下， 变压器设计专家系统[3]应运而生. 变压器设计问题不能用具体的函数形式求解， 只能用尝试变换再判断的方法， 因此专家系统中初始方案的质量一定程度上决定设计周期的长短和设计结果的好坏. 然而现有的变压器设计专家系统确定初始方案一般都是直接法， 即根据用户的要求和已有方案凭经验给出初始方案， 因此存在大量的主观因素. 针对这个问题， 人们引进了数学的方法， 如模糊理论的方法[4]， 对已有的多个方案进行综合评价， 相对客观、 完善的确定初始方案. 本文运用加权灰靶理论的方法[5-9]， 对此问题进行决策， 并分别从待解决问题的特点、 加权灰靶理论和模糊理论的标准序列的选取方法以及两种方法的决策结果等方面进行了分析， 证明了加权灰靶理论方法的特殊适用性.

1 加权灰靶理论的决策方法

加权灰靶理论[10]是运用灰色理论的知识处理模式序列的一种分析方法， 包括靶心度分析和贡献度分析. 按照命题要求在模式序列中找到最靠近目标值的数据构造标准模式， 各模式与标准模式一起构成灰靶， 标准模式即为灰靶的靶心. 然后对其它序列进行模式识别， 模式变换， 并计算模式接近靶心的程度， 即靶心度分析； 由于各指标对模式靶心度的影响不同， 将各指标对靶心度影响的程度进行分析， 即贡献度分析.

加权灰靶理论的实现过程： 首先针对被决策的事件集提出待选方案集和评价指标集， 根据评价指标的不同极性， 确定灰靶的靶心. 用各方案对应各指标的属性值与靶心向量构造决策矩阵. 由于各指标的极性、 量纲不同， 需对决策矩阵进行模式识别和模式变换， 将决策矩阵的属性值统一为正极性， (0,1)之间的值. 其次对各指标进行权重计算， 即灰贡献度分析， 将变换后的决策矩阵进行加权处理. 最后求得各方案与靶心的距离， 进行靶心度分析， 靶心距越小方案越合理.

1.1 决策矩阵R的确定

确定被决策事件集A={a1,a2,a3,…,an}， 从数据库中选出初步符合条件的方案集B={b1,b2,b3,…,bn}， 确定各个评价指标， 构成指标集合V={v1,v2,v3,…,vn}， 根据B和V确定理想最优决策方案r0， 列出方案集B对指标集合V的决策矩阵

通常， 在应用加权灰靶理论进行灰度决策时， 参考序列即理想最优决策方案是未知的. 由于不同事件不同评价指标存在不同的极性， 因此， 设计者在构造理想最优决策方案时， 可以根据不同的极性找到对策矩阵的参考向量r0. 一般情况下， 评价指标的极性分为极大值极性、 极小值极性和适中值极性. 不同极性计算参考向量的公式如下：

1.2 无量纲处理

由于事件ai的各个评价指标vj的属性值的量纲不一致， 导致数据差异大， 不能进行直接比较， 所以要对R进行统一变换. 要求变换后的数据均为正极性， 且都为(0,1)之间的数据. 针对指标的不同极性模式变换公式如下：

变换后的对策矩阵

1.3 加权处理

对于多目标决策问题， 方案由多个评价指标构成， 方案的优劣与指标有关. 由上述可知， 灰靶贡献度就是考虑各个评价指标对方案优劣的影响程度， 即求得每个评价指标的相对重要程度， 最简单的方法就是计算评价指标的权重. 权重分主观权重和客观权重. 对于设计型专家系统初始方案的选择问题， 主观权重反应了设计者的丰富经验； 客观权重反应了各指标间客观存在的联系. 本文采用主观的层次分析法和客观的熵权法进行灰贡献度计算. 层次分析法的权重由变压器设计专家依据丰富的设计经验以及用户要求给定. 熵权重则是由系统熵确定. 熵是评价系统无序程度的一个度量， 一般指标的信息熵越小， 该系统有序度越大， 权重就应该越高.

层次分析法的权重

熵权法权重的求法：

1) 求各指标在各方案中所占的概率

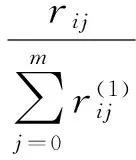
2) 求各指标的熵值

3) 求各指标的有序度

4) 求各指标的熵权重

总灰贡献度为

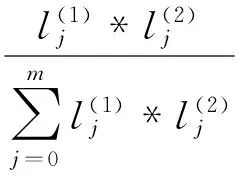
1.4 靶心及靶心距的确定

1) 经加权处理的决策矩阵

2) 靶心

3) 靶心距

si=

1.5 加权灰靶评估

将各个方案下的靶心距进行比较， 靶心距越小， 方案越接近标准值越优. 最优方案即为靶心距最小的方案.

2 实例验证

2.1 实验设计

本文以10 kV级不同容量油浸式配电变压器为例， 以用Microsoft Visual C++ 6.0开发环境建立的变压器设计专家系统为平台， 对基于加权灰靶理论决策方法确定专家系统的最优初始方案进行了实例验证. 并将该方法的决策结果与用模糊数学理论方法所得结果进行了对比、 分析.

本文被决策的事件集A={a1,a2,a3}={确定容量为200 kVA油浸式配电变压器设计专家系统的初始方案； 确定容量为315 kVA油浸式配电变压器设计专家系统的初始方案； 确定容量为500 kVA油浸式配电变压器设计专家系统的初始方案}； 评价指标集合V={v1,v2,v3,…,v7}={短路损耗、 空载损耗， 阻抗电压， 高压温升， 低压温升， 空载电流， 成本}； 方案集Bi={bi1,bi2,bi3,bi4}，i=1,2,3， 具体内容为符合条件的待选初始方案数据， 如表 1 所示.

由此列出方案集Bi对指标集合V的决策矩阵Ri， 并对其进行上述基于加权灰靶理论的相应操作， 得到决策结果. 需要注意的是， 本文在进行灰贡献度分析时， 以计算各评价指标的权重来衡量其贡献度， 而主观权重即层次分析法所得的权重由设计者根据对各指标侧重点不同凭设计经验给出， 本案例中各容量的主观权重均为l(1)={0.16,0.12,0.10,0.16,0.14,0.14,0.18}.

作为评价函数对各设计方案进行决策， 从而确定最优方案.

表 1 待选初始方案数据Tab.1 The data of proposed scheme

2.2 结果分析

利用加权灰靶理论、 模糊理论两种不同的方法对10 kV级容量分别为200, 315, 500 kVA的油浸式配电变压器设计专家系统最优初始方案的确定进行实例验证的结果如表 2 所示.

表 2 比较分析结果Tab.2 The results of comparative analysis

由上述可知， 加权灰靶理论和模糊理论两种数学方法无论在解决问题的基本思想上， 还是在标准序列的选取上， 以及对表 1 中待选初始方案的决策结果上都存在差异. 本文变压器设计专家系统初始方案的确定方法为从已有的几个符合各项指标要求的合格方案中通过综合评价选出最优的作为初始方案. 在方案均符合要求的情况下要求各损耗越小越好， 而不是越接近标准值越优. 因此模糊理论中， 以各指标的额定值作为标准， 以标准量化公式求得各方案接近标准值的方法就不尽合理. 而且模糊理论中求得各方案的欧几里得距离为其它序列与标准序列向量间的平均距离， 对各指标对方案影响程度不同的场合， 此决策方法将难以顺利发挥作用. 加权灰靶理论在确定变压器设计专家系统初始方案的问题上有更强的适用性. 由表2中两种方法的决策结果可知， 利用加权灰靶理论所得方案比灰理论所得方案的各项指标值都低， 模糊理论所得方案较加权灰靶理论得到方案的各项指标只是更接近于指定值， 而加权灰靶理论所得结果更优， 验证了上述分析结果.

3 结 论

本文提出了一种基于加权灰靶理论的决策方法， 运用该方法对已有的变压器设计方案进行综合评价， 从而确定变压器设计专家系统的最优初始方案. 并将此方法的结果与模糊理论方法的评价结果进行比较分析， 从理论和实验结果上说明了加权灰靶理论的适用性. 克服了传统变压器设计专家系统通过直接法确定初始方案的不足， 使此过程更加科学、 完善.

[1] 李俊萍， 盖国权. 基于自适应遗传算法的电力变压器优化设计[J]. 电子设计工程， 2015， 23(8)： 129-131.

Li Junping， Gai Guoquan. Optimization design of a power transformer by automatically adaptive genetic algorithm[J]. Electronic Design Engineering， 2015, 23(8)： 129-131. (in Chinese)

[2] 潘再平， 张震， 潘晓弘. 基于QPSO算法的电力变压器优化设计[J]. 电工技术学报， 2013, 28(11)： 42-47.

Pan Zaiping， Zhang Zhen， Pan Xiaohong. Optimal design of power transformers using quantum-behaved particle swarm optimization[J]. Transactions of China Electrotechnical Society ， 2013， 28(11)： 42-47.(in Chinese)

[3] Hernandez C， Arjona M A. Design of an efficient distribution transformer based on an expert system and FE[C]. Proceeding of the IEEE Conference on Electrical Machines (ICEM), 2010： 1-5.

[4] 赵振卫， 王秀和， 孙兴东. 永磁直流电动机初始设计方案的事例模糊设计法[J]. 电机与控制学报， 2001， 5(3)： 159-162.

Zhao Zhenwei， Wang Xiuhe， Sun Xingdong. The fuzzy case design method of permanent magnet direct current motor preliminary design scheme[J]. Electric Machines and Control， 2001, 5(3)： 159-162. (in Chinese)

[5] Li Shuwei， Yang Jie， Zhang Dongsheng. Application of weighted gray target theory in health status assessment of electromechanical actuating system[C]. Proceedings of IEEE International Conference on Mechatronics and Automation, 2014： 3-6.

[6] Luo Dang， Zhang Jing. The development model of new energy vehicle in Henan Province based on the weighted grey target decision[C]. Proceedings of IEEE International Conference on Grey Systems and Intelligent Services, 2011： 597-600.

[7] 雷春燕， 刘从法， 罗日成. 基于多目标智能加权灰靶理论的电力变压器状态维修决策[J]. 电力科学与技术学报， 2013， 28(2)： 85-88.

Lei ChunYan， Liu Congfa， Luo Richeng. Condition-based maintenance decision of transformer based on multi-attribute intelligent grey target[J]. Journal of Electric Power Science and Technology， 2013, 28(2)： 85-88. (in Chinese)

[8] 郑玲峰， 王建元， 白志亮， 等. 用改进灰靶理论评价变压器状态[J]. 中国电力， 2011， 44(1)： 28-31.

Zheng Lingfeng， Wang Jianyuan， Bai Zhiliang， et al. Transformer state evaluation based on improved grey target theory[J]. Electric Power， 2011, 44(1)： 28-31. (in Chinese)

[9] 刘思峰， 袁文峰， 盛克勤. 一种新型多目标智能加权灰靶决策模型[J]. 控制与决策， 2010， 25(8)： 1159-1163.

Liu Sifeng， Yuan Wenfeng， Sheng Keqin. Multi-attribute intelligent grey target decision model[J]. Control and Decision， 2010， 25(8)： 1159-1163. (in Chinese)

[10] 邓聚龙. 灰理论基础[M]. 武汉： 华中科技大学出社， 2002.

声明

本刊已许可中国学术期刊(光盘版)电子杂志社在中国知网及其系列数据库产品中，以数字化方式复制、汇编、发行、信息网络传播本刊全文。该社著作权使用费与本刊稿酬一并支付。作者向本刊提交文章发表的行为即视为同意我编辑部上述声明。

DecisionMethodResearchonInitialSchemeofTransformerDesignExpertSystem

DU Jiang1， ZHANG Ye-ye1， WANG Jing-qin1， YUE Shuai2

(1. Province-Ministry Joint Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability，Hebei University of Technology， Tianjin 300130， China；. The Capital Aerospace Machinery Company， Beijing 100071， China)

An approach to determine the optimal initial solution based on the weighted grey target theory was proposed considering the problem of the current transformer design expert system cannot determine the initial solution intelligently according to the existing design. The approach included approaching degree analysis and contribution degree analysis .How to determine the initial solution of 10 kV level oil-immersed distribution transformer design expert system was demonstrated on the basis of building weighted grey target theory mathematical decision model .The feasibility and superiority of the method is verified by comparing with the results obtained by the fuzzy theory method.

transformer； expert system； weighted grey target theory

1673-3193(2017)05-0587-05

2016-06-20

河北省人社厅项目(A2013007001)； 河北省科学技术研究与发展项目(13210129)； 河北省科技支撑计划项目(12212171)

杜 江(1972-)， 男， 副教授， 博士， 主要从事变压器优化设计和现代智能仿生算法及其应用研究.

TM402

A

10.3969/j.issn.1673-3193.2017.05.014