非自治Fitzhugh-Nagumo方程在周期边界下的整体解

张 珊， 柴玉珍

(太原理工大学 数学学院， 山西 太原 030024)

非自治Fitzhugh-Nagumo方程在周期边界下的整体解

张 珊， 柴玉珍

(太原理工大学 数学学院， 山西 太原 030024)

Hodgkin-Huxley方程是描述神经纤维膜电流、 膜电压关系的微分方程， Fitzhugh-Nagumo方程是Hodgkin-Huxley方程的简化模型.讨论了具有周期边界的非自治FitzHugh-Nagumo系统在外刺激下的初边值问题， 首先利用Galerkin方法及常微分方程理论证明了具有周期边界的非自治Fitzhugh-Nagumo方程存在局部解; 其次利用了一种新的方法对局部解作一致先验估计证明了整体解的存在性; 最后利用Gronwall不等式证明了非自治Fitzhugh-Nagumo系统整体解的唯一性.

Fitzhugh-Nagumo系统； 非自治方程； 外刺激项； Galerkin方法； Gronwall不等式

FitzHugh-Nagumo方程是一类描述了在高于阈值的常电流刺激下神经元动作电位的周期性振荡的非线性演化方程， 同时也是一个著名的反应扩散模型， 这类模型在实际中有广泛的应用， 因此是近年来很多学者研究的热点方程之一.这类方程是由Richard FitzHugh和南云仁一于1961年由H-H模型[1]简化得到的一个二维系统， 亦即F-N模型[2]

ut=uxx+f(u)-v,vt=δu-γv.

近年来人们对神经脉冲传导的F-N方程做了很多研究[3-5]， 如M.Osman Gani和Toshiyuki Ogawa分析了广义F-N模型的不稳定周期行波解[6], Gianni Arioli和 Hans Kochb研究了F-N方程的旅游脉冲解的存在性和稳定性[7]， 吴永辉等研究较为广义F-N方程组的整体吸引子及惯性流形[8], 简化了P.Constantin等人的工作， 王慕洁等讨论了F-N模型以2D为周期的初值问题[9-10]， 但是对外刺激下的非自治神经元传导模型研究得甚少.

本文研究非自治F-N系统在周期边界条件下的初边值问题

边界条件和初值条件为

式中：u表示跨膜电压的特性;v描述钾激活和钠失活的慢变过程;I1(x,t,u),I2(x,t,u)为外加刺激电流项(外刺激项依赖于时间变量、 空间变量以及它们的函数)， 且x∈Ω，Ω为R上的有界区间，a,λ,b是非负常数，f∈L2(Ω),g∈L2(Ω).

1 预备知识

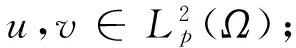
P2)h是一个非线性光滑函数, 且满足

h(s)s≥0,h(0)=0,h′(s)≥-c,s∈R,

|h′(s)|≤c(1+|s|r),s∈R,

其中,n≤2,r≥0, 当n≥3时,

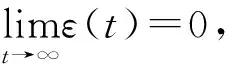
P4)I1(x,t,u),I2(x,t,u)关于x,t可测, 对u连续， 且∀t>0, ∃0≤hi(x,t)∈L2(0,t,L2(Ω)),i=(0,2), ∃0≤hj(x,t)∈L2(0,t,L∞(Ω)),j=(1,3), 使得

I1(x,t,u)≤h0+h1|u|,

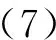
|fg|dx≤‖f‖Lp(Ω)‖g‖Lq(Ω).

引理3[12-15]已知Φ(t) (t∈R+)是绝对连续的正值函数， 且存在ε>0使得微分不等式

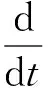
成立. 其中存在α≥0和a∈[0,1]， 使得g(t)满足

存在β≥0， 使得h(t)满足

|h(y)|dt≤β,

α,β是与t无关的常数.则存在γ(γ是与α和ε有关的常数)使得

成立.

2 主要结果及其证明

式中：αjm,βjm为未知函数. 那么由Galerkin方法可知，um,vm应满足下面的常微分方程组

(umt-aΔum+λum+h(um)+vm-f(x)-

(vmt-ε(t)(um-bum+g(x)+

再由peano定理, 方程(8)～(9)满足初始条件

的解在[0,tN]上存在. 其中, 初值ajm,bjm的选取满足

由常微分方程理论, 方程(8)～(10)存在唯一局部解um,vm.

下面对um,vm作一致先验估计.

引理4 假设式(5)～(7)成立， 则对方程(8)和(9)的近似解um,vm有如下估计

ε(t)‖um‖2+‖vm‖2≤γ[ε(0)‖um(0)‖2+‖vm(0)‖2]eη1t+ρ, ∀t>0,

证明在式(8)中令ωs=ε(t)um, 在式(9)中令ωs=vm， 两式相加有

(umt-aΔum+λum+h(um)+vm-f(x)-I1m(x,t,u),ε(t)um)+

对式(12)利用分部积分及格林函数有

对式(13)右边各项利用引理1和引理2， 可得

以及

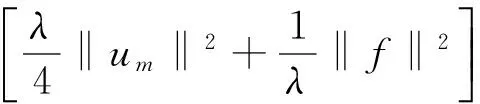
将上述估计代入式(13)有

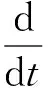
2aε(t)‖

式(14)两边同时加上

karctan(t+t0)[ε(t)‖um‖2+‖vm‖2].

其中

karctant0≥

t0为大于零的常数， 令Φ(t)=ε(t)‖um‖2+‖vm‖2，

则有

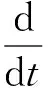
(∀t∈R+),

其中

由ε(t)的假设

由引理3知

ε(t)‖um‖2+‖vm‖2≤

γ[ε(0)‖um(0)‖2+‖vm(0)‖2]eη1t+ρ.

再对式(14)从[0,2D]积分即完成引理的证明.

引理5 若满足引理4的条件， 则有

ε(t)‖um‖2+‖vm‖2≤M1,

式中：Mi(i=1～3)及以下诸引理中的Mi均为与N无关的常数.

证明用-ε(t)Δum与式(8)作内积， 用-Δvm与式(9)作内积, 两式相加得

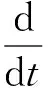
2bε(t)‖vm‖2=2ε(t)(h(um),Δum)-2ε(t)[(f,Δum)+(g,Δvm)+

利用Sobolev不等式、 引理1和引理2对式(15)估计有

2ε(t)(h(um),Δum)=-2ε(t)(h(um),um)=-2ε(t)(h′(um)um,um)≤2cε(t)‖um‖2·

(I1(x,t,um),Δum)≤‖h0‖2‖Δum‖+‖h1‖∞‖um‖‖um‖≤

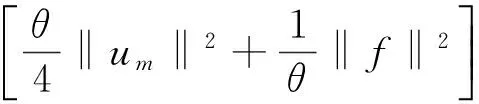
同理

(I2(x,t,vm),Δvm)≤‖h2‖2‖Δvm‖+‖h3‖∞‖vm‖‖vm‖≤

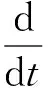
3ε(t)‖Δvm‖2≤Q1(t)[ε(t)‖um‖2+

将式(17)从0～2D积分， 得

[ε(t)‖um‖2+‖vm‖2]+

记

Wm(t)=[ε(t)‖um‖2+‖vm‖2]+

则

Wm(t)≤

其中 0≤Qi(t)∈L1(0,t),i=1,2.

由前述假设知，Wm(0)对N一致有界， 从而

由Gronwall不等式， 并利用引理4的结论即得本引理的证明.

注意到上面估计式中各常数M均为与N无关， 因此由紧致性原理即有下面的结论.

推论在定理1的假设下， 有

‖u‖∞+‖v‖∞≤C, ∀t≥0,

其中,C是与‖u0‖1, ‖v0‖1有关与t无关的常数.

定理2 在定理1的条件下， 方程(8)～(10)的整体解是唯一的.

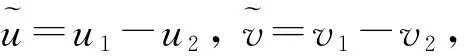
利用微分中值定理得

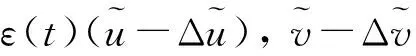
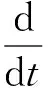
由Gronwall不等式和式(20)有

[1] Hodgkin A L, Huxley A F. A quantitative description of membrane current and its applications to conduction and excitation in nerve[J]. J. Physiol., 1952(117)： 500-544.

[2] FitzHugh R. Impulses and physiological states in theoretical models of nerve membrane[J]. J. Biophys, 1961(1)： 445-446.

[3] Zhou Shengfan, Wang Zhaojuan. Finite fractal dimensions of random attractors for stochastic FitzHugh-Nagumo system with multiplicative white noise[J]. J. Math. Anal. Appl., 2016(441)： 648-667.

[4] Zheng Qianqian, Shen Jianwei. Pattern formation in the FitzHugh-Nagumo model[J]. Computer & Mathematics with Applications, 2015, 70(5)： 1082-1097.

[5] Jia Junyi, Liu Haihong, Xu Chenglin, et al. Dynamic effects of time delay on a coupled FitzHugh-Nagumo neural system[J]. Alexandria Engineering Journal, 2015, 54(2)： 241-250.

[6] Osman Gani M, Toshiyuki Ogawa. Instability of periodic traveling wave solutions in a modified FitzHugh-Nagumo model for excitable media[J]. Applied Mathematics and Computation, 2015, 256(1)： 968-984.

[7] Gianni Arioli, Hans Koch. Existence and stability of traveling pulse solutions of the FitzHugh-Nagumo equation[J]. Nonlinear Analysis, 2015(113)： 51-70.

[8] 吴永辉， 王明新 .广义FitzHugh-Nagumo方程组的整体吸引子及惯性流形[J]. 应用数学学报， 1996, 19(2)： 185-195.

Wu Yonghui, Wang Mingxin. Global attractor of the generalized FitzHugh-Nagumo equations and its inertial manifold[J]. Applied Mathematics, 1996, 19(2)： 185-195. (in Chinese)

[9] 王慕洁, 张仲. Fitzhugh-Nagumo神经传导方程的周期初值问题[J]. 数理医药学杂志, 2000, 13(1) ： 13-14.

Wang Mujie, Zhang Zhong. Fitzhugh-Nagumo nerve conduction equation of the periodic initial value problem[J]. Journal of Mathematical Medicine, 2000, 13(1) ： 13-14. (in Chinese)

[10] 郑宋穆, 沈玮熙. Fitzhugh-Nagumo方程组初边值问题的整体存在性[J]. 科学通报, 1984(16)： 966-969.

Zheng Songmu, Shen Weixi. Fitzhugh-Nagumo equations, the global existence of the initial-boundary value problem [J]. Chinese Science Bulletin, 1984(16)： 966-969. (in Chinese)

[11] 王术, 空间与偏微分方程引论[M]. 第1版. 北京： 科学出版社， 2009.

[12] Xie Yongqin, Deng Jianbin. Global attractors for a class of nonlinear evolution equations[J]. Mathematical Theory and Application, 2010, 30(4)： 13-19.

[13] Pata V, Squassina M. On the strongly damped wave equation[J]. Communications in Mathematical Physics, 2005, 253(3)： 511-533.

[14] Pata V, Zelik S. Smooth attractors for damped wave equation[J]. Nonlinearity, 2006(19)： 1495-1506.

[15] Xie Y Q, Zhong C K. Asympotic behavior of a class of nonlinear evolution equations[J]. Nonlinear Anal., 2009(71)： 5095-5105.

IntegralSolutionofNon-AutonomousFitzhugh-NagumoEquationUnderthePeriodicBoundary

ZHANG Shan, CHAI Yu-zhen

(College of Mathematics, Taiyuan University of Technology, Taiyuan 030024, China)

Hodgkin-Huxley is a kind of differential equation describes the relations of nerve fiber membrane electric current and the membrane voltage and it is a simplified model of Hodgkin-Huxley. The initial-boundary value problem of non-autonomous Fitzhugh-Nagumo system with periodic boundary under the external stimulation is discussed. Firstly, using the Galerkin method and theory of ordinary differential equations the existence of local solution of non-autonomous Fitzhugh-Nagumo equations with periodic boundary; Secondly, with a new method of local solution for consistent prior estimate proves the existence of global solution; Finally, using Gronwall inequality proves the uniqueness of global solutions of non-autonomous Fitzhugh-Nagumo system as a whole.

Fitzhugh-Nagumo systems; non-autonomous equation; outside stimulus items; Galerkin method; Gronwall inequality

1673-3193(2017)05-0531-05

2016-07-06

张 珊(1991-)， 女， 硕士， 主要从事偏微分方程及应用研究.

O241.8

A

10.3969/j.issn.1673-3193.2017.05.005