基于Fluent自振脉冲射流腔体结构参数的数值优化

张 洪， 祝锡晶， 赵 韡， 石亦琨

(1. 中北大学 机械与动力工程学院， 山西 太原 030051； 2. 煤与煤层气共采国家重点实验室， 山西 晋城 048000；3. 首都航天机械公司， 北京 100044)

基于Fluent自振脉冲射流腔体结构参数的数值优化

张 洪1,2， 祝锡晶1， 赵 韡1,2， 石亦琨3

(1. 中北大学 机械与动力工程学院， 山西 太原 030051； 2. 煤与煤层气共采国家重点实验室， 山西 晋城 048000；3. 首都航天机械公司， 北京 100044)

自激振荡脉冲射流可以有效提高深部煤岩破蚀效率. 为设计破蚀煤岩效率较高的自激振荡脉冲射流发生装置， 基于流体力学基本原理， 利用Fluent软件对自激振荡脉冲射流进行数值模拟， 分析不同的腔体结构对脉冲射流峰值速度的影响. 采用大涡模型(LES)进行计算， 通过数值模拟发现， 自激振荡脉冲射流速度云图和压力云图符合涡旋碰撞理论和脉冲射流发生原理. 在特定的参数(腔长L=4.5 mm, 腔径D=8 mm， 下碰撞壁收敛角α=120°， 上下喷嘴直径分别为d1=1 mm，d2=1.1 mm)下， 自激振荡脉冲射流峰值速度最大， 为231.21 m/s， 相比于入口速度提高了92.68%， 脉冲射流冲蚀效果较好.

破蚀煤层； 自激振荡； 脉冲射流； 大涡模拟

0 引 言

煤炭资源为我国提供了70%的能源， 支撑着国民经济的快速发展. 我国的煤层气资源丰富， 2014年底全国煤层气探明地质储量达7 000亿立方米. 煤层气的开发利用， 可以减少甲烷对大气的污染[1]. 高瓦斯压力和高地应力的综合作用是造成煤与瓦斯问题突出的主要原因， 并且开采过程中产生的煤尘会引发爆炸和肺病等危害[2]， 极大地影响了煤层气开采效率.

自激振荡脉冲射流是通过流体力学、 流体弹性力学、 流体共振和水声学等发展起来的一种新型高效脉冲射流， 它不需要外加激励元件， 依靠流体本身在自激振荡腔中产生振荡， 将连续射流变为脉冲射流[3-4]. 自激振荡脉冲射流相比于连续射流有很好的破岩效果， 在脉冲振幅为250 m/s时， 自激振荡脉冲射流破岩的效率提高了48.7%， 在脉冲频率为2.5 kHz时， 自激振荡射流的破岩效率提高了29.3%[5]. 裴江红[6]等证明了脉冲峰值频率取决于系统的固有频率和系统阻尼比， 当来流脉动主频率和系统固有频率相近时脉冲射流峰值压力可以达到最大. 刘新阳[7]等研究了结构参数和运行参数对于自激振荡脉冲射流的影响. 唐川林[8]等系统地研究了自激振荡腔体结构对于自激振荡脉冲射流性质的影响， 对于自激振荡脉冲射流的腔体结构进行了优化. 王乐勤[9]等对低压大流量自激振荡脉冲射流喷嘴系统进行了试验研究， 优化了自激喷嘴结构参数并与高压小流量喷嘴结构参数进行了对比.

自激振荡脉冲射流能够产生较强的冲蚀作用， 可以有效地切割破蚀煤岩. 本文通过Fluent流体仿真软件对不同结构参数的自激振荡腔进行仿真研究， 探讨自激振荡腔内液体的流动状态， 并优化自激振荡腔体结构参数(腔长L、 腔径D、 下碰撞壁收敛角α和下喷嘴直径d2)， 优化后的结构参数可作为自激振荡脉冲射流发生装置设计依据， 并将射流发生装置用于开采煤岩.

1 激振荡腔体几何模型及数学模型

1.1 自激振荡腔的几何模型

自激振荡脉冲射流装置是轴对称结构， 射流的分布也具有对称性. 因此， 将自激振荡射流发生装置简化为X-Y平面上的二维问题， 如图 1 所示.

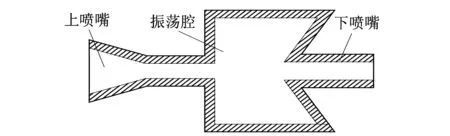
图 1 自激振荡腔的几何模型Fig.1 Geometric model of the self-excited oscillation cavity

1.2 自激振荡腔数学模型

自激振荡脉冲射流流动方式为湍流， 湍流数值模拟的方法包括雷诺平均模拟(RANS)、 直接模拟(DNS)和大涡模拟(LES). 对比三种模拟的方法可知， 雷诺平均数值模拟把变量做均化处理， 比较难以得到射流脉动的细节， 直接模拟对计算机的要求很高， 一般难以达到其要求， 而大涡模拟正好介于直接模拟和雷诺平均模拟之间， 而且能够较好地描述脉冲射流的脉动过程[10-11]. 因此， 文中选用大涡模拟的方法对自激振荡脉冲射流进行数值模拟， 并以射流峰值速度为监测指标， 优化自激振荡腔的几何参数.

1.2.1 大涡模拟控制方程

在进行大涡过程中， 为对大涡流场模拟计算， 并对小涡流场建立模型， 要通过滤波处理将大涡和小涡流场分开. 在大涡模拟中， 瞬时流动变量被分解为大尺度量和小尺度量， 可以用物理区域上的加权积分来表示大尺度量.

本文大涡模拟使用BOX滤波函数.

对完全的N-S方程

进行滤波， 得到

其中，τij通过涡粘性模型来模拟.

自定义涡粘性系数为

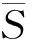
式中： Smagorinshy常数Cs=0.1； 滤波宽度Δ=(Δx2+Δy2+Δz2)1/2, Δx2, Δy2和Δz2分别是在x,y和z方向上的网格宽度.

由于经典的Smagorinshy涡粘性模型近壁面区域湍流行为不能准确地给出， 因此可在壁面附近进行处理. 依据Van Driest的指数粘滞函数， 修正Smagorinshy模型的涡粘性系数

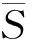
将式(4)， 式(6)代入式(3)中， 得到控制方程

2 CFD几何建模和自激振荡腔流场的建立

2.1 模型的建立

利用ICEM CFD软件对自激振荡腔体结构进行网格划分， 选用四面体非结构性网格， 并对自激振荡腔拐角处和圆柱段的网格进行加密处理.

自激振荡脉冲射流发生装置的结构参数对能否形成良好的脉冲射流有重要的影响. 因此， 用Fluent仿真软件， 探讨自激振荡脉冲射流装置腔长L、 腔径D、 下喷嘴直d2、 下碰撞壁收敛角α对自激振荡脉冲射流性质的影响， 自激振荡腔几何参数如表 1 所示.

表 1 自激振荡腔几何参数Tab.1 Geometric parameters of self-excited oscillation cavity

2.2 边界条件设置

采用Fluent软件对自激振荡脉冲发生装置进行数值分析， 其边界条件设置如下： 入口边界条件定义为压力入口(Pressure-inlet)， 出口边界条件定义为压力出口(Pressure-outlet)， 出口压力设置为0(1个大气压)， 其他边界条件设置为壁面条件(Wall).

3 结果分析与讨论

3.1 Fluent模拟效果分析

图 2 为腔长L=2.5 mm， 腔径D=8 mm， 上、 下喷嘴直径分别为d1=1 mm，d2=1.2 mm， 初始压力p1=5 MPa， 计算总时间为t=0.002 s时， 自激振荡脉冲射流速度云图随时间的变化情况.

图 2 不同时刻自激振荡脉冲射流速度状态Fig.2 Velocity state of self-excited oscillation pulse jet in different time

图 2 为不同时刻的速度云图. 当t=0.000 05 s时， 射流进入振荡腔与腔内的空气发生动量交换产生不稳定剪切层并即将形成涡环， 这时候中心轴线上速度变化较小. 当t=0.000 1 s时， 自激振荡腔内已经产生了明显的涡环， 并且涡环随着射流向下游运动与下游碰撞壁碰撞产生反馈， 这时中心轴线速度变化仍不明显. 当t=0.000 15 s 时， 涡环与碰撞壁碰撞后产生的反馈开始向上游运动， 这时中心轴线上速度较前一时刻速度变大， 涡环中心处的速度值最大. 当t=0.000 5 s 时， 涡环经过不稳定剪切层的选择放大， 逐渐形成了大尺度的涡环， 中心轴线上速度云图颜色有变化但不明显， 说明还未产生明显的脉冲射流. 当t=0.001 s时， 振荡腔内涡环逐渐趋于稳定. 当t=0.002 s时， 自激振荡腔内形成稳定且往复循环的大尺度涡环， 振荡腔中心轴心上的速度有较为明显的变化， 振荡腔内形成了效果较好的脉冲射流. 自激振荡脉冲射流瞬时速度云图的变化符合自激振荡脉冲射流的发生机理.

3.2 自激振荡腔长对脉冲射流性质的影响

设定振荡腔上、 下喷嘴直径分别为d1=1.0 mm,d2=1.2 mm， 腔径D=8 mm， 下碰撞壁收敛角α=120°. 通过改变振荡腔长与前喷嘴直径之比L/d1探索自激振荡腔长对射流性质的影响规律， 如图 3 所示. 不同的初始压力， 在相同条件下， 脉冲射流的峰值速度随着振荡腔长的增加而增大， 当腔长增加到一定程度时峰值速度开始下降， 说明存在着一个最佳腔长使自激振荡脉冲射流的冲击效果最好. 形成这种现象的原因是自激振荡脉冲射流要求振荡腔内的反馈和扰动有一定的相位关系， 如果腔长过短， 射流在腔体中未形成有效的振荡就从后喷嘴喷出. 如果振荡腔过长， 射流在振荡腔内流动变得复杂， 能量耗散较大， 峰值速度降低.

图 3 不同泵压下振荡腔腔长与峰值速度的关系Fig.3 The relationship between the cavity length and the peak velocity under different pump pressures

从图 3 中可以看出， 在L/d1=4.5， 也就是腔长L=4.5 mm时自激振荡效果最优. 在相同条件下， 自激振荡脉冲射流的峰值速度随着初始压力的增大而呈现非线性增长， 初始压力越大， 峰值速度越大.

3.3 自激振荡腔直径对射流性质的影响

自激振荡腔径是影响脉冲射流效果的主要参数之一， 取优化后腔长L=4.5 mm，d1=1.0 mm，d2=1.2 mm，α=120°. 探寻腔径对自激振荡脉冲射流性质的影响， 如图 4 所示. 由自激振荡脉冲射流峰值速度随腔径与上喷嘴直径之比变化情况可知， 初始泵压不变时， 相同条件下自激振荡脉冲射流峰值速度随着腔径的变大先增大后减小， 当D=7 mm时， 脉冲射流峰值速度最大. 形成这种现象的原因是， 当腔径较小时， 振荡腔内不能形成较好的大尺度涡环， 脉冲射流效果较差. 当腔径较大时， 自激振荡腔内流动形式较为紊乱， 能量耗散较大， 所以射流的峰值速度较低.

图 4 不同泵压下自激振荡腔腔径与峰值速度的关系Fig.4 Relationship between cavity diameter and peak velocity of self-excited oscillation cavity under different pump pressures

3.4 下喷嘴直径对于射流性质的影响

保持腔长L=4.5 mm,D=8 mm,d1=1.0 mm,p1=5 MPa不变， 对下喷嘴直径d2进行优选. 图5为下喷嘴直径与自激脉冲射流峰值速度的关系曲线. 由图可知， 下喷嘴直径对自激振荡脉冲射流性质有一定的影响. 在相同的压力条件下， 自激振荡脉冲射流峰值速度随着下喷嘴直径的增大先增加后减小， 存在一个最优的值d2=1.1 mm. 形成上述趋势的原因为， 下喷嘴直径过小， 射流在进入圆柱段管路时急剧收缩， 能量损失较大从而影响射流流出的速度. 当下喷嘴直径过大时， 由自激振荡脉冲射流发生原理可知， 上、 下喷嘴直径相差过大不易在前喷嘴出口处形成“涡”的放大， 导致自激振荡脉冲射流效果较差， 从而影响冲蚀煤层的效率.

从图 5 分析可知， 当上、 下喷嘴直径分别为d1=1 mm,d2=1.1 mm， 腔长L=4.5 mm， 腔径D=8 mm时， 自激振荡脉冲射流峰值速度最大， 冲蚀煤层的效果最好. 当给定初始压力为p1=5 MPa时， 自激振荡脉冲射流的峰值速度为231.21 m/s， 相比上喷嘴入口速度提高了92.68%， 有效提高了射流的冲击力.

图 5 不同腔长条件下喷嘴直径与射流峰值速度的关系Fig.5 Relationship between nozzle diameter and jet peak velocity under different cavity length

3.5 碰撞壁收敛角α对脉冲射流性质的影响

保持优化参数L=4.5 mm，D=7 mm，d2=1.1 mm不变， 取下碰撞壁收敛角分别为90°， 120°， 150°， 180°和210°. 通过数值模拟得出自激振荡脉冲射流峰值速度与下碰撞壁收敛角的关系， 如图 6 所示. 高速射流在振荡腔内能否形成有效的反馈， 振荡腔碰撞壁是其关键结构之一. 碰撞壁的收敛角度合适， 射流经过碰撞壁能够形成较强的压力扰动波， 有利于形成较好的脉冲射流.

图 6 不同泵压下碰撞壁收敛角α与峰值速度的关系Fig.6 The relationship between the angle of convergence of the wall and the peak velocity under different pump pressures

从图 6 可知， 相同条件下， 脉冲射流峰值速度随着收敛角的不同有较大的变化. 初始压力不同时， 脉冲射流峰值速度变化的趋势基本一致， 收敛角为120°时脉冲射流的峰值速度最大. 在相同条件下， 自激振荡脉冲射流峰值速度随着初始泵压的增大而增大.

4 结 论

利用Fluent流体计算软件， 采用大涡模型对自激振荡喷嘴进行了数值模拟， 得出以下结论：

1) 从数值模拟云图可知， 射流在振荡腔内形成了明显的涡环， 振荡腔内的压力变化和速度变化符合涡旋碰撞理论和脉冲射流发生机理.

2) 自激振荡腔长、 腔径、 下喷嘴直径和下碰撞壁收敛角对脉冲射流峰值有较大影响， 当腔长L=4.5 mm， 腔径D=7 mm， 下喷嘴直径d2=1.1 mm， 下碰撞壁收敛角α=120°， 脉冲射流峰值速度最大， 优化后的自激振荡腔结构参数可作为自激振荡脉冲射流发生装置的设计准则.

3) 在相同的条件下， 自激振荡脉冲射流峰值速度随着初始压力的增大呈现非线性增长， 在一定范围内初始压力越大， 峰值速度越大.

4) 当初始泵压p1=5 MPa， 腔长L=4.5 mm， 腔径D=7 mm， 上、 下喷嘴直径分别为d1=1 mm,d2=1.1 mm时， 自激振荡脉冲射流峰值速度为231.21 m/s， 相比于入口初始速度(120 m/s)提高了92.68%， 说明自激振荡脉冲射流可以产生较好的冲蚀效果.

[1] Han F X, Lindner J S, Wang C. Making carbon sequestration a paying proposition[J]. The Science of Nature, 2007, 94(3)： 170-182.

[2] 许满贵， 魏攀， 何鹏程， 等. 表面活性剂降尘效果试验研究[J]. 煤炭技术， 2016， 35(3)： 139-142.

Xu Mangui， Wei Pan， He Pengcheng， et al. Experiment study on efficiency of reducing dust by using surfactants[J]. Coal Technology， 2016， 35(3)： 139-142. (in Chinese)

[3] Keller J J. Non-linear self-excited acoustic oscillations in cavities[J]. Journal of Sound & Vibration， 1984， 94(3)： 397-409.

[4] Ozalp C， Pinarbasi A， Rockwell D. Self-excited oscillations of turbulent inflow along a perforated plate[J]. Journal of Fluids & Structures， 2003， 17(7)： 955-970.

[5] 周维. 自激振荡脉冲射流破岩特性数值模拟[D]. 重庆： 重庆大学， 2014.

[6] 裴江红， 廖振方， 唐川林， 等. 自激振荡脉冲射流频率特性实验研究[J]. 中国机械工程， 2009， 20(1)： 60-63.

Pei Jianghong， Liao Zhenfang， Tang Chuanlin， et al. Experimental study on characteristics of self-excited oscillation pulsed water jet[J]. China Mechanical Engineering， 2009， 20(1)： 60-63. (in Chinese)

[7] 刘新阳， 王松林， 高传昌， 等. 自激脉冲射流装置参数对性能影响试验研究[J]. 振动与冲击， 2012， 31(24)： 112-114.

Liu Xinyang， Wang Songlin， Gao Chuanchang, et al. Effects of parameters of a self-excited pulsed jet equipment on its performance[J]. Journal of Vibration and Shock， 2012， 31(24)： 112-114. (in Chinese)

[8] 唐川林， 王晓明， 胡东， 等. 自振脉冲喷嘴中异形结构对射流振荡频率的影响[J]. 矿山机械， 2015， 43(1)： 15-20.

Tang Chuanlin， Wang Xiaoming， Hu Dong, et al. Influence of special-outlet self-exciting oscillation pulsed nozzle on oscillation frequency[J]. Mining Machinery， 2015;43(1)： 15-20. (in Chinese)

[9] 王乐勤， 王循明， 徐如良， 等. 低压大流量自激振荡脉冲射流喷嘴结构参数优化研究[J]. 流体机械， 2004， 32(3)： 7-10.

Wang Leqin， Wang Xunming， Xu Ruliang， et al. Structure-parameter optimized study of self-exicited oscillation pulsation-jet nozzle in low-press and amount-flux[J]. Fluid Machinery， 2004， 32(3)： 7-10. (in Chinese)

[10] 肖友刚， 张晓缝， 康志成. 高速列车车头曲面脉动压力的大涡模拟[J]. 四川大学学报(工程科学版)， 2010， 42(1)： 227-232.

Xiao Yougang， Zhang Xiaofeng， Kang Zhicheng. Large eddy simulation for fluctuation pressure of high speed train head surface[J]. Journal of Sichuan University (Engineering Science Edition)， 2010， 42(1)： 227-232. (in Chinese)

[11] 赵新泽， 汪坤， 徐翔， 等. 风琴管空化清洗喷嘴结构改进及数值分析[J]. 科学技术与工程， 2015， 15(35)： 131-137.

Zhao Xinze， Wang Kun， Xu Xiang， et al. Structure improvement and numerical analysis of organ pipe cavitation cleaning nozzle[J]. Science Technology and Engineering， 2015， 15(35)： 131-137. (in Chinese)

NumericalOptimizationoftheStructureParametersoftheSelf-VibrationPulseJetCavityBasedonFluent

ZHANG Hong1,2, ZHU Xi-jing1, ZHAO Wei1,2, SHI Yi-kun3

(1. School of Mechanical and Power Engineering, North University of China, Taiyuan 030051, China；2. Coal and Coal-Bed Methane Mining State Key Laboratory, Jincheng 048000, China；3. The Capital Aerospace Machinery Company， Beijing 100044, China)

The efficiency of deep coal rock burst can be effectively improved by self-excited oscillation pulsed jet. In order to design the self-excited oscillation pulsed jet device with higher coal rock burst efficiency , based on the basic principle of fluid mechanics, Fluent software is used to do the numerical simulation of the self-excited oscillation pulsed jet, and to do the analysis of the influence of cavity structure of different pulse jet peak velocity. The large eddy model (LES) is used to calculate. The numerical simulation shows that the velocity chart and pressure cloud diagram of self-excited oscillation pulse jet accord with the vortex collision theory and the principle of pulse jet generation. The peak velocity of self-excited oscillation pulsed jet is gotten under the particular parameters (LengthL=4.5 mm, Cavity diameterD=8 mm, Collision wall convergence angle alphaα=120°, the upper and lower nozzles diameter are respectivelyd1=1 mm,d2=1.1 mm), The maximum velocity of self-excited oscillation pulsed jet is 231.21 m/s, which is 92.68% higher than that of inlet velocity, and the effect of pulse jet erosion is better.

broken coal seam; self-excited oscillation; pulsed jet; large eddy simulation

1673-3193(2017)05-0556-05

2017-03-02

山西省煤层气联合研究基金资助项目(2015012018)； 中北大学研究生科技立项资助项目(20161308,20161309)

张 洪(1991-)， 男， 硕士生， 主要从事自激振荡磨料水射流技术研究.

赵 韡(1987-)， 男， 讲师， 博士， 主要从事磨料水射流技术和水液压相关研究.

TE377； TD823

A

10.3969/j.issn.1673-3193.2017.05.009