互连耦合网络的SIR传染病模型
李淑萍
(中北大学 理学院, 山西 太原 030051)
互连耦合网络的SIR传染病模型
李淑萍
(中北大学 理学院, 山西 太原 030051)
考虑了包含层内接触和层间接触的双层相互连接的耦合网络, 研究了基于该网络的SIR 传染病模型. 利用渗流理论和概率生成函数, 研究了疾病的流行阈值和流行前疾病的平均暴发规模, 分析了层内传播和层间传播对疾病传播的影响. 通过研究发现, 层内传播存在, 引发疾病流行的层间传染率的临界值降低和流行规模增加.
互连耦合网络; 渗流; 概率生成函数; 流行阈值; 平均暴发规模
0 引 言
目前, 关于网络拓扑结构对传染病传播的影响, 大多局限于单个网络, 然而现实世界中往往是多种病毒在单一种群中的传播或同一病毒分别在不同种群的内部和种群之间的传播. 现实世界中的诸多复杂系统是由许多不同结构与功能的单个网络耦合而成的, 即耦合网络, 其中的单个网络仅仅是整个网络中的一个子网络. 根据耦合网络中的节点属性将耦合网络分为两类, 一类是节点属性相同, 边的属性不同的多重耦合网络; 一类是节点属性不同的耦合网络. 文献[1-4]给出耦合网络拓扑结构的定义框架及统计刻画, 并总结了网络属性对网络上的动力学的影响.
伴随着耦合网络拓扑结构的研究, 基于耦合网络的疾病传播研究也不断涌现. 针对节点属性相同, 边的属性不同的多重耦合网络, Wu等建立了基于多重网络的SIS的平均场模型, 并分析了疾病的流行阈值, 给出了多重网络的一般免疫策略理论[5]. 传染病的传播可以映射为网络的键渗流问题[6-10], 即疾病可以依一定的概率沿着网络中的占用边(染病接触边)而传播, 疾病传播的平均暴发规模则是从初始的染病节点出发, 沿着占用边能到达的网络的连通规模. 利用键渗流理论, Hackett等提出了多重网络的键渗流分析方法, 并利用该方法得到巨连通组成部分的规模和占用概率的临界值. 结果表明, 在层间相关和不相关的多重网络中, 多重网络和其单部投影网络的渗流阈值都是相同的; 进一步地, 当多重网络的度分布都是poisson分布时, 多重网络和其单部投影网络渗流的巨连通组成规模也是相同的[11]. 基于多重耦合网络的耦合强度, Dickison等给出了两类耦合网络: 强耦合网络和弱耦合网络, 研究了两类耦合网络上的疾病传播, 发现了两种不同的传播机制. 在强耦合系统中, 系统的两个子网络之间的相互连接增强了疾病的传播, 流行总是在整个耦合系统中发生, 在弱耦合网络中, 当传染强度小于临界值时, 疾病只在一个子网内部流行, 在整个耦合网络不会流行[12]. Funk等考虑到多种病原体在多重网络中的传染病传播, 研究了带有任意联合度分布、 任意重叠数量和免疫强度的重叠网络中, 两种不同菌株传播的边渗流之间的相互作用. 发现如果两个网络的度是正相关, 那么第一种菌株的暴发对第二个网络中的另一种菌株的暴发具有免疫作用, 并且, 如果两个网络的度分布的异质性越强, 保护作用越强. 另一方面, 如果度分布是不相关或者负相关, 度分布的异质性增强会使得第二种疾病的传播更为困难[13]. 考虑到重叠网络中节点重叠比例对疾病传播的影响, Buono等给出了一类节点重叠比例为q的部分重叠的重叠网络, 利用分支过程研究了重叠网络上的SIR疾病传播过程. 发现随着重叠比例q的增加, 整个系统的传播阈值减小[14].
考虑到耦合网络的节点属性不同, 2002年, Newman利用渗流理论研究了基于二部图的疾病传播的SIR模型[6], 文献[6]中仅考虑了疾病在不同性别人群之间的传播, 而忽略了疾病在相同性别人群之间的传播. 将文献[6]中的二部图看作一个双层网络, 文献[6]仅考虑了疾病的层间传播, 而忽略了疾病的层内传播. 文献[15]中尽管用推广的Miller模型讨论了互联耦合网络的SIR模型, 比较了各个子网与整个网络的再生数的大小关系, 并没有找到再生数之间的明确关系. 为此, 本文将利用渗流理论, 进一步地研究基于图 1 的双层互联耦合网络的疾病传播的SIR模型, 将网络中的一层记为m层, 另一层记为f层. 假定网络中的每个个体都具有双度指标, 其中, 一个度表示节点的自身所属层内的度; 另一个度表示节点的层间的度.

图 1 双层互联耦合网络Fig.1 Double-layer coupling network
1 互联耦合网络及概率生成函数

式中:pm,qm分别是只有m层接触或只有f层接触的m层节点占本层所有节点的比例, 1-pm-qm为既有m层接触又有f层接触的m层节点占本层所有节点的比例, 相应地有,pf,qf分别是只有f层接触或只有m层接触的f层节点占本层所有节点的比例, 1-pf-qf为既有m层接触又有f层接触的f层节点占本层所有节点的比例,ζ为Riemann zeta函数.
为了利用渗流理论研究网络上的疾病传播, 有必要给出网络联合度分布的概率生成函数. 定义m层节点的联合度分布的概率生成函数为
基于此生成函数及式(1)和式(2), 可以知道m层节点周围平均m层邻居数和平均f层邻居数
〈i〉m=
〈j〉m=
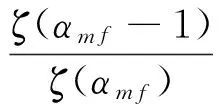


类似地, 沿任意一条f-m边到达的m层节点的余度分布的生成函数为

对于f层节点, 相应地有联合度分布的生成函数
f层节点的平均m层邻居数和平均f层邻居数为

沿任意一条m-f边到达的f层节点的余度分布的生成函数为
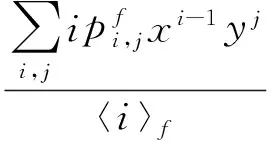
沿任意一条f-f边到达的f层节点的余度分布的生成函数为
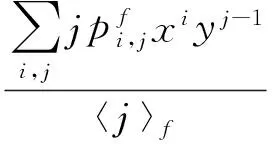
2 互联耦合网络上的疾病传播
下面考虑疾病在网络上的传播. 假设一个疾病从网络中的某一个节点开始传播. 因为网络中有同层接触和异层接触, 相应地存在疾病的层内传播和层间传播. 层内传播: 染病m层节点通过同层接触传染易感m层节点, 染病f层节点通过同层接触传染易感f层节点; 层间传播: 染病m层节点通过异层接触传染易感f层节点, 染病f层节点通过异层接触传染易感m层节点. 综上, 一共有四种传染方式. 因此, 假设单位时间内, 在上述四类接触过程中, 平均每次接触并传染的概率分别为:Tmm,Tmf,Tff,Tfm. 假设染病节点治愈后永久免疫, 不再参与疾病的传播, 即网络中的节点一共有三种状态,S态,I态和R态. 由于染病节点不会再返回到易感节点, 网络中的每条边至多发生一次疾病的传播, 所以,可以利用渗流理论来研究网络上疾病的传播. 为了研究的方便, 令Tmf=Tfm=T.
2.1 疾病传播网络的概率生成函数
为了解决这个渗流问题, 需要知道网络中每个节点周围的占用边的分布, 为此修正上一节中的概率生成函数. 对于一个有i个m层邻居和j个f层邻居的m层节点, 假设分别有a条m-m边和b条m-f边被占用, 那么层节点的占用边分布的生成函数

Gm(1+(x-1)Tmm,1+(y-1)T),

gmm(x,y;Tmm,T)=
Gmm(1+(x-1)Tmm,1+(y-1)T),
沿任意一条f-m边到达m层节点的剩余占用边分布的生成函数
gfm(x,y;Tmm,T)=
Gfm(1+(x-1)Tmm,1+(y-1)T).
类似地, 对于f层节点相应地有占用边的分布的生成函数
gf(x,y;T,Tff)=
Gf(1+(x-1)T,1+(y-1)Tff),
及沿任意一条m-f边到达f层节点的剩余占用边分布的生成函数
gmf(x,y;T,Tff)=
Gmf(1+(x-1)T,1+(y-1)Tff).
沿任意一条f-f边到达f层节点的剩余占用边分布的生成函数
gff(x,y;T,Tff)=
Gff(1+(x-1)T,1+(y-1)Tff).
为了研究疾病的暴发规模, 需要给出上述生成函数的一些性质
gX(1,1;Tmm,T)=GX(1,1)=1,
gXY(1,1;Tmm,T)=GXY(1,1)=1,
(X=m,f;Y=m,f),

注意到, 当x=1,y=1时,GX(1,1)=1,GXY(1,1)=1, 且记
一旦网络的联合度分布给定, 可以得到
其中,
〈i2〉m=
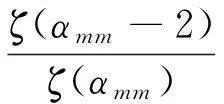
〈j2〉m=
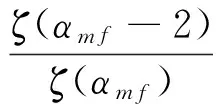
〈j2〉f=
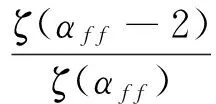
〈i2〉f=



为了书写方便, 引入下面记号, 记
2.2 流行阈值和暴发规模
利用生成函数, 可以预测疾病传播的平均暴发规模. 定义Φm(w;T)(Ψf(w;T))为从网络中任意一个m(f)层节点出发经过占用边到达的连通规模分布的生成函数, 其中,T=(Tmm,T,Tff). 为了预测疾病传播的平均暴发规模, 需要知道从任意一条m-m边出发经过占用边到达的连通的规模. 如果任意选择一条边, 那么疾病传播的可能传播途径如图 2 所示, 可能被选择的m-m边没有发生疾病传播(图中用虚线表示), 可能选择的m-m边发生疾病传播(图中用实线表示), 但到达的m层节点没有其他的接触邻居, 或除了那条被选择的边之外, 还有一个其他m(f)层的邻居传染, 或除了那条被选择的边之外, 还有两个其他m层邻居或两个f层邻居或一个m层邻居一个f层邻居被传染等等. 如果任意选择一条f-m边, 那么疾病的可能传播途径如图 3 所示, 定义Φmm(w;T)为从任一条m-m边出发经占用边到达的连通规模分布的生成函数,Φfm(w;T)为从任一条f-m边出发经占用边到达的连通规模分布的生成函数,Φmf(w;T)为从任一条m-f边出发经占用边到达的连通规模分布的生成函数,Φff(w;T)为从任一条f-f边出发经占用边到达的连通规模分布的生成函数. 显然有
Φm(w;T)=wgm(Φmm(w;T),Φmf(w;T);Tmm,T),
Φf(w;T)=wgf(Φfm(w;T),Φff(w;T);T,Tff),
其中,Φmm(w;T),Φfm(w;T),Φmf(w;T),Φff(w;T) 满足下列方程组

图 2 从任意选择一条m-m边出发的可能传播途径Fig.2 All possible transmission routes emanated from any chosen m-m edge

图 3 从任意选择一条f-m边出发的可能传播途径Fig.3 All possible transmission routes emanated from any chosen f-m edge
对式(7)两端求导可得
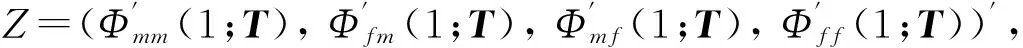
将式(8)写成下列矩阵形式
AZ=B,
从式(9)可求得
detA=

当degA>0时, 方程组(8)有解
].
利用上述解可得到从任意一个m层节点出发的疾病传播的平均暴发规模为

从任意一个f层节点出发的疾病传播的平均暴发规模为

当detA≤0时, 疾病流行.

其中,


进一步地, 可以得到层间传播的流行阈值

如果给定Tmm和Tff, 当T>Tc时, 疾病将在整个网络中流行.
从式(10)中可得

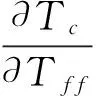

2) 当网络中的参数取值为下列几种特殊情况时, 有
①qm=qf=1
网络中所有节点仅有异层接触, 原来的网络变成了一个二部图网络, 所以, 〈i2〉m=〈i〉m=〈j2〉f=〈j〉f=〈ij〉m=〈ij〉f=0, 疾病流行的条件为


此时的阈值条件与文献[1]中的疾病流行条件相同.
②pm=pf=1
网络中所有节点都只有同层接触时, 原来的网络变成了两个不连通的子网络:m层节点构成的网络和f层节点构成的网络. 疾病在两个网络中的传播是相互独立的. 疾病在两个网络中流行的条件分别为
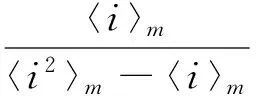

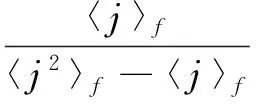

③pm+qm=1,pf+qf=1

3 模拟与敏感性分析

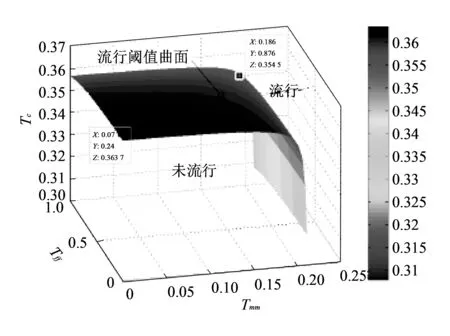
图 4 流行阈值曲面Fig.4 The surface of epidemic thresholds
下面考虑传染率对平均暴发规模的影响. 为了分别研究Tmm,Tff和T对平均暴发规模的影响, 需要固定两个参数而让另一个参数变化. 首先, 固定层内传染概率, 考虑层间传染概率的影响. 从图 4 中的临界值曲面上取参数值, 分别取两组层内传染概率Tmm=0.186,Tff=0.876 和Tmm=0.028,Tff=0.24, 从图 5(a) 可以看到, 在层间传染概率T到达临界值时, 平均暴发规模非常小. 如果取Tmm=0.186,T=0.354 5 和Tmm=0.028,T=0.362 7, 从图5(b)可以看到, 当Tff到达临界值时, 平均暴发规模最大能达到8×103. 如果取T=0.354 5,Tff=0.876 和T=0.362 7,Tff=0.24, 当Tmm到达临界值时, 平均暴发规模都超过了104. 比较图 5 中的图形, 发现Tmm和Tff对疾病的暴发规模影响较大, 尤其是m层层内传播影响更大.
因此, 为了消除或减小疾病流行风险, 应当控制层间传播的传染率, 使之小于临界值Tc, 当未达到流行之前, 减小层内传播的传染率Tmm和Tff, 可有效控制疾病的染病规模.

图 5 疾病的平均暴发规模Fig.5 Average outbreak size of diseases
4 结 论
通过将双层接触网络拆分为层内接触网络和层间接触网络, 假设网络中的每个节点都具有两个度, 分别表示给定节点在各个层内的邻居数, 利用渗流理论, 得到了网络上SIR模型的传染病的流行阈值曲面(即疾病流行时, 层内流行阈值和层间流行阈值满足的条件), 并研究了不同传染率对疾病传播的平均暴发规模的影响. 与文献[6]中的结论相比, 发现当仅考虑层间传播而忽略层内传播时, 引起疾病流行的层间传染概率临界值被高估. 说明层内传播存在, 引发疾病流行的层间传染率的临界值降低, 疾病在整个双层耦合网络中流行的风险增加. 另外, 由于层内网络结构不同,m层层内传播的临界值容易达到, 故m层层内传播比f层层内传播引发疾病流行的风险要大. 疾病未达到流行时, 控制层内传播的传染率, 可有效控制疾病的平均暴发规模.
[1] Gao J, Buldyrev S V, Stanley H E, et al. Networks formed from interdependent networks[J]. Nature physics, 2012, 8(1): 40-48.
[2] Boccaletti S, Bianconi G, Criado R, et al. The structure and dynamics of multilayer networks[J]. Physics Reports, 2014, 544(1): 1-122.
[3] Xu X L, Qu Y Q, Guan S, et al. Interconnecting bilayer networks[J]. Euro phy Lett, 2011, 93(6) : 68002.
[4] Zou S R, Zhou T, Liu A F, et al. Topological relation of layered complex networks[J]. Phys Lett A, 2010, 374(43) : 4406-4410.
[5] Wu Q, Lou Y, Zhu W. Epidemic outbreak for an SIS model in multiplex networks with immunization[J]. Mathematical Biosciences, 2016, 277: 38-46.
[6] Newman M E J. Spread of epidemic disease on networks[J]. Physical review E, 2002, 66(1): 016128.
[7] Meyers L A. Contact network epidemilogy: bond percolation applied to infectious disease prediction and control[J]. Bull. Amer. Math. Soc., 2007, 44: 63-86.
[8] Sander L M, Warren C P, Sokolov I M, et al. Percolation on heterogeneous networks as a model for epidemics[J]. Mathematical Biosciences, 2002, 180(1): 293-305.
[9] Meyers L A, Newman M E J, Martin M, et al. Applying network theory to epidemics: control measures for Mycoplasma pneumoniae outbreaks[J]. Emerging Infectious Diseases, 2003, 9(2): 204-210.
[10] Meyers L A, Pourbohloul B, Newman M E J, et al. Network theory and SARS: predicting outbreak diversity[J]. Journal of Theoretical Biology, 2005, 232(1): 71-81.
[11] Hackett A, Cellai D, Gómez S, et al. Bond percolation on multiplex networks[J]. Physical Review X, 2016, 6(2): 021002.
[12] Dickison M, Havlin S, Stanley H E. Epidemics on interconnected networks[J]. Physical Review E, 2012, 85(6): 066109.
[13] Funk S, Jansen V A A. Interacting epidemics on overlay networks[J]. Physical Review E, 2010, 81(3): 036118.
[14] Buono C, Alvarez-Zuzek L G, Macri P A, et al. Epidemics in partially overlapped multiplex networks[J]. PloS One, 2014, 9(3): e92200.
[15] Koch D, Illner R, Ma J. Edge removal in random contact networks and the basic reproduction number[J]. Journal of Mathematical Biology, 2013, 67(2): 217-238.
SIRInfectiousDiseaseModelonInterconnectedCouplingNetworks
LI Shu-ping
(School of Science, North University of China,Taiyuan 030051, China)
Referring to different transmission probabilities of intra-layer contacts and inter-layer contacts, an infectious model on interconnected networks with intra-layer and inter-layer contact patterns was proposed. With the framework of probability generation function, the surface of the critical value could accurately be obtained, which helped to evaluate whether the disease would be epidemic or not, and the average size of infection when there was no epidemic. Interestingly, it is unveiled that, compared with the case of purely inter-layer contact, the outbreak threshold of inter-layer transmission is overestimated in the bipartite network and inter-layer transmission plays a determinate role in activating the larger-scale infection. In addition, it is shown that intra-layer transmission is the major risk of increasing the number of disease incidences before the formal outbreak of diseases.
interconnected coupling network; percolation; probability generating function; epidemic threshold; average outbreak size
1673-3193(2017)05-0505-08
2016-11-15
山西省应用基础研究面上青年基金项目(201601D021015)
李淑萍(1979-), 女, 讲师, 博士, 主要从事复杂网络和动力系统的研究.
O211.65
A
10.3969/j.issn.1673-3193.2017.05.001

