高阶非齐次线性微分方程解的增长级
周 鉴, 龙见仁
(贵州师范大学 数学科学学院, 贵州 贵阳 550001)
高阶非齐次线性微分方程解的增长级
周 鉴, 龙见仁
(贵州师范大学 数学科学学院, 贵州 贵阳 550001)
运用微分方程复振荡的理论, 研究一类具有整函数系数的高阶非齐次复线性微分方程解的增长级, 其中方程的系数均为整函数且非齐次项不恒为零. 当方程的系数增长级满足一定的条件时, 方程任一非零解具有无穷增长级.
线性微分方程; 增长级; 整函数; 零点收敛指数

考虑给定k≥2阶线性微分方程
式中:Ai(i=0,1,…,k-1),F均为整函数且F不恒为零.
方程(1)对应的齐次方程为

定理1 设k≥2为自然数,A0,A1,…,Ak-1,F均为有穷级整函数且F不恒为零, 存在As(0≤s≤k-1) 使得对于正实数α>0,β>0, 有ρ(Ai)<β(i≠s)及ρ(F)<β且
i) 或者max{ρ(A),i=1,…,s-1}>ρ(A0)>ρ(F).
ii) 或者ρ(Ai)<ρ(F), (i=0,1,…,s-1).
如果对于任意给定的ε>0, 存在有穷实数序列{φm}, {θm}满足条件
φ1<θ1<φ2<θ2<…<φn<θn<φn+1=
且
使得当z→∞,φm≤argz≤θm(m=1,…,n)有

则
1) 方程(1)的任意不恒为零解f满足

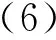
2) 对于任意的有穷级整函数φ有
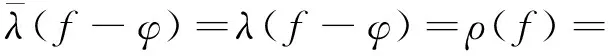

定理2 设k≥2为自然数,A0,A1,…,Ak-1,F均为有穷级整函数且F不恒为零, 存在As(0≤s≤k-1) 使得对于正实数α>0,β>0, 有ρ(Ai)<β(i≠s)及ρ(F)≥β, 且max{ρ(Ai),i=1,…,s-1}>ρ(A0).
如果对于任意给定的ε>0, 存在有穷实数序列{φm}, {θm}满足条件(3),(4) 使得式(5)成立, 则
1) 方程(1)的任意解f满足式(6), 至多一个有穷级解f0.


3) 如果f为方程(1)中的无穷级解,φ有穷级整函数但非方程(1)的解则
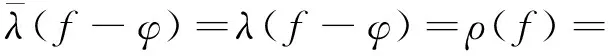
∞.
4) 如果f0为(1)中的有穷级解, 则对于方程(1)中的任一无穷级解f及任意常数c≠1有
∞.
1 预备知识
引理1[10]设f(z)为一个有穷ρ级超越亚纯函数, 对于给定的正数ε存在一个线性零测度集E1⊂[0,2π), 使得如果ψ1∈[0,2π)E1, 则存在一个常数R1(ψ1)>1使得对所有满足条件: argz=ψ1且|z|≥R1(ψ1)的复数z及所有的实数对(k,j)这里k>j≥0, 有不等式

引理2[11]设f(z)是整函数, |f(k)(z)|在某条射线argz=θ上无界, 则存在无穷序列zn=rneiθ(n=1,2,…)趋于无穷, 使得rn→∞时有f(k)(zn)→∞且
|zn|k-j

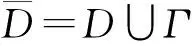
引理4 设k≥2为自然数,A0,A1,…,Ak-1, 均为整函数, 对于给定实数α>0,β>0,θ1<θ2, 存在As(0≤s≤k-1), 当z→∞,z∈S={z∶θ1≤argz≤θ2}有
Why does the“ the first generation of Post-00 s” win “the first generation of Post-90 s” in daily chemical industry? 5 50

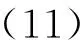
如果f为方程(2)非零解且ρ(f)=ρ<∞, 则对于任意ε>0, 存在M>0, 成立不等式|f(z)|≤M|z|s. 其中z∈Sε={z∶θ1+ε≤argz≤θ2-ε}, |z|≥R0>0.
证明由ρ(f)=ρ<∞, 由引理1知, 存在一个线性零测度集E1⊂0,2π), 使得如果ψ0∈[0,2π)E1, 则存在常数R0=R0(ψ0)>1使得对所有满足条件: argz=ψ0且|z|≥R0(ψ0)的复数z及i=s+1,…,k有

下证|f(s)(z)|在任意射线argz=ψ∈[θ1,θ2]E1上有界.
反设|f(s)(z)|在某条射线argz=ψ1∈[θ1,θ2]E1上无界, 由引理2知, 存在无穷序列zn=rneiψ1(n=1,2,…)趋于无穷, 使得rn→∞时有f(s)(zn)→∞且
|zn|s-i≤
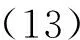
由方程(2)有



结合式(11)~(13)有
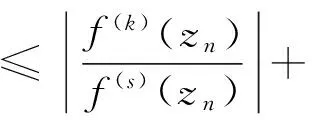



式中:M0,M1为某个正实数. 这与式(10)相矛盾.
进一步由引理3易知, 存在M2>0, 使得任意的z∈Sε={z∶θ1+ε≤argz≤θ2-ε}有

由f(z)的s阶Taylor展开式
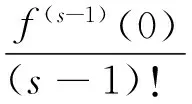
故
|f(z)|≤|f(0)|+|f′(0)||z|+…+

式中:M为某个正实数且z∈Sε, |z|≥R0>0.
引理5 设k≥2为自然数,A0,A1,…,Ak-1,α,β,ε,θ1,θ2,Sε, 如引理4所给,F为整函数且ρ(F)<β, 则对于方程(1)的任意有穷级解f有|f(z)|≤M|z|s. 其中z∈Sε, |z|≥R0>0,M为某个正实数.
证明由ρ(f)=ρ<∞及引理4的证明可知式(12)仍然成立.
下证|f(s)(z)|在任意射线argz=ψ∈[θ1,θ2]E1上有界.
反设|f(s)(z)|在某条射线argz=ψ1∈[θ1,θ2]E1上无界, 由引理4证明可知式(13)成立.
由于|f(s)(zn)|→∞, (n→∞), 不妨设|f(s)(zn)|≥1, 注意到ρ(F)<β, 故

结合式(1), 式(11)~(13), 式(18)可得



M0exp{o(1)|zn|β}|zn|M1,
其中,M0,M1为某个正实数. 这与式(10)相矛盾.
同引理4的证明, 可得
f(z)|≤M|z|s,
其中,M为某个正实数且z∈Sε, |z|≥R0>0.
引理6 设k≥2为自然数,A0,A1,…,Ak-1为有穷级整函数, 存在As(0≤s≤k-1)使得对于α>0,β>0有

如果对于任意给定的ε>0, 存在有穷实数序列{φm}, {θm}满足条件(3)和(4) 使得当z→∞,z∈Dm={z∶φm≤argz≤θm, (m=1,…,n)}有

则方程(2)的任意解f均为无穷级.


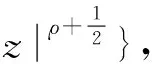
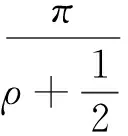
则当|z|=r>r0+1时, 有
故在角域θm-ε≤argz≤φm+1+ε, (m=1,…,n)中, 当|z|=r>r0+1时, 有
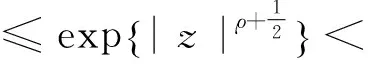

如果多项式f的次数degf≥s, 则
ρ(f(k)+Ak-1f(k-1)+…+A0f)=
ρ(As)≥β>0.
这与方程(2)相矛盾.
如果多项式f的次数degf≤s-1, 则
ρ(As-1f(s-1)+…+A0f)>ρ(A0)≥0,
这也与方程(2)相矛盾.
故方程(2)的任意解f均为无穷级.
引理7 设k≥2为自然数,A0,A1,…,Ak-1,α,β,ε,{φm},{θm},Dm, 如引理6所给,F为整函数且ρ(F)<β, 且成立
i) 或者ρ(Ai)<ρ(F), (i=01,,…,s-1),
ii) 或者max{ρ(Ai),i=1,…,s-1}>ρ(A0)>ρ(F),
则方程(1)的任意解f均为无穷级.


同理, 在角域θm-ε≤argz≤φm+1+ε, (m=1,…,n)可得|f(z)|≤M|z|s.
由此可知, |f(z)|≤M|z|s全平面成立, 因此f(z)为多项式.
如果多项式f的次数degf≥s, 则
ρ(f(k)+Ak-1f(k-1)+…+A0f)=
ρ(As)≥β>ρ(F),
这与方程(1)相矛盾.
如果多项式f的次数degf≤s-1, 则
i) 当ρ(Ai)<ρ(F), (i=0,1,…,s-1)时,
ρ(f(k)+Ak-1f(k-1)+…+A0f)=
max{ρ(Ai)∶i=0,1,…,s-1}<ρ(F).
这与方程(1)相矛盾.
ii) 当max{ρ(Ai),i=1,…,s-1)>ρ(A0)>ρ(F)时,
ρ(As-1f(s-1)+…+A0f)=max{ρ(Ai)∶
i=0,1,…,s-1)}≥ρ(A0)>ρ(F),
这也与方程(1)相矛盾.
故方程(1)的任意解f均为无穷级.
引理8[13]设A0,A1,…,An-1,F≠0为有穷级亚纯函数,f为方程
2 定理的证明
定理1的证明
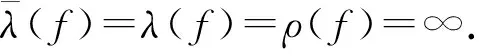
2) 令g=f-φ, 由于f为方程(1)的解, 且ρ(φ)<∞, 故
ρ(g)=ρ(f-φ)=max{ρ(f),ρ(φ)}=
ρ(f)=∞.
而f=g+φ, 将其代入方程(1)中有
g(k)+Ak-1g(k-1)+…+A0g=
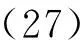
由于ρ(φ)<∞, 故φ不可能为方程(1)的解, 因此,
记G=F-(φ(k)+Ak-1φ(k-1)+…+A0φ)≠0, 则对于方程
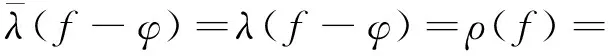
∞.
定理2的证明
1) 不妨设f0为方程(1)的一个有穷级解, 即ρ(f0)<∞.
如果方程(1) 还有另外一个有穷级解f1, 满足ρ(f1)<∞且f0≠f1.
由增长级的定义可知

另外,f0-f1显然应满足方程(2).
由引理6可知
ρ(f0-f1)=∞, 这与ρ(f0-f1)<∞相矛盾.
故方程(1)至多有一个有穷级解.
再由引理8知, 方程(2)的任一无穷级解f应满足


2) 设f0为方程(1)中的有穷级解,ρ(f0)<∞, 则由方程(1)可知, 当z0为f0的d阶零点且d>k, 则z0必为F的d-k阶零点, 因此
又由值分布理论的对数导数引理知识可知
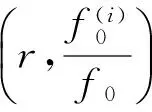
由方程(1)可得
故

由式(33), (34)和(36)有

记α=max{ρ(As),ρ(F)}, 则对于任意ε>0及充分大的r, 有
T(r,F) 由式(37)和(38)有 故 ρ(f0)≤max{ρ(F),ρ(As)}. 另一方面由方程(1)可见 ρ(f0)≥max{ρ(F),ρ(As)}. 故 3) 设f为方程(1)中的无穷级解,φ为有穷级整函数但非方程(1)的解. 令g=f-φ, 则ρ(g)=ρ(f-φ)=max{ρ(f),ρ(φ)}=ρ(f)=∞. 而f=g+φ, 将其代入方程(1)中有 g(k)+Ak-1g(k-1)+…+A0g= F-(φ(k)+Ak-1φ(k-1)+…+A0φ). 又φ非方程(1)的解, 因此 F-(φ(k)+Ak-1φ(k-1)+…+A0φ)≠0. 4) 设f0为方程(1)中的有穷级解, 则对于方程(1)中的任一无穷级解f及任意常数c≠1, 令g=f-cf0, 则g满足方程 g(k)+Ak-1g(k-1)+…+A0g=(1-c)F. [1] 杨乐. 值分布及其新研究[M]. 北京: 科学出版社, 1982. [2] Hayman W K. Meromorphic function[M]. Oxford: Clarendon, 1964. [3] 张广厚. 整函数和亚纯函数理论-亏值、 渐进值和奇异方向[M]. 北京: 科学出版社, 1986. [4] Chen Zongxuan, Gao Shian. Entire solutions of differential equations with finite order transcendental entire coefficients[J]. Acta Mathematica Sinica, 1997, 13(4): 453-464. [5] Li Yezhou, Wang Jun. Oscillation of solution of linear differential equations[J]. Acta Mathematica Sinica , 2008, 24(1): 167-176. [6] Wang Jun, Laine I. Growth of solutions of nonhomogeneous linear differential equations[J]. Abstract &Applied Analysis, 2009, 2009(1): 1-11. [7] Habib H, Beladi B. On the growth of solutions of some higher order linear differential equations with entire coefficients[J]. Theory Differential Equations, 2011, 93(2): 1-13. [8] Long Jianren. On complex oscillation theory of solutions of some higher order linear differential equations[J]. Journal of Math Research with Applications, 2012, 32(4): 423-430. [9] Grohn J, Rattya J. On oscillation of solutions of linear differential equations[J]. Journal of Geometric Analysis, 2015, 20(5): 1-18. [10] Gunderson G G. Estimates for the logarithmic derivative of meromorphic function plus similar estimates[J]. Journal of the London Mathematical Society, 1988, 37(2): 88-104. [11] Laine I, Yang Ronghua. Finite order solutions of complex linear differential equations [J]. Electronic Journal of Differential Equations, 2004, 2004(65): 281-286. [12] Chen Zongxuan, Gong Juan, Zheng Xiumin. On the growth of solutions to higher order differential equations[J]. Annals of Differential Equations, 2012, 2(2): 170-179. [13] 高仕安, 陈宗煊, 陈特为. 线性微分方程的复振荡理论[M]. 武汉: 华中理工大学出版社, 1998. GrowthofSolutionsofNon-HomogeneousHigherOrderLinearDifferentialEquations ZHOU Jian, LONG Jian-ren (School of Mathematics science, Guizhou Normal University, Guiyang 550001, China) This paper concerned with the growth of solutions of the non-homogeneous higher order linear differential equations with entire function coefficients by using complex oscillation theory of linear differential equations, where the coefficients are entire functions and the non-homogeneous term unequal to zero. It is shown when the coefficients order meets certain conditions then every non-zero solution of the equation is of infinite order. linear differential equations; growth; entire function; convergence exponent of zero 1673-3193(2017)05-0544-05 2016-09-30 国家自然科学基金资助项目(11501142); 贵州省科学技术基金(黔科合J字LKS[2009]04号) 周 鉴(1976-), 男, 副教授, 博士生, 主要从事复分析的研究. O174.52 A 10.3969/j.issn.1673-3193.2017.05.007