源荷储一体化的广义灵活电源双层统筹规划

李海波, 鲁宗相, 乔 颖

(1. 清华大学电机工程与应用电子技术系, 北京市 100084; 2. 电力系统及发电设备控制和仿真国家重点实验室, 清华大学, 北京市 100084; 3. 清华四川能源互联网研究院,四川省成都市 610200)

源荷储一体化的广义灵活电源双层统筹规划

李海波1,2,3, 鲁宗相1,2, 乔 颖1,2

(1. 清华大学电机工程与应用电子技术系, 北京市 100084; 2. 电力系统及发电设备控制和仿真国家重点实验室, 清华大学, 北京市 100084; 3. 清华四川能源互联网研究院,四川省成都市 610200)

高比例可再生能源电力系统中,逐渐减少的传统机组灵活性资源与增加的灵活性需求之间的矛盾日益严重,开展灵活电源专题规划的必要性日益凸显。基于灵活性供需平衡机理,提出了源荷储一体化的广义灵活电源概念,并建立了含资源投资决策和运行模拟校验的双层统筹规划模型。在证明了规划模型的凸性基础上,基于最大净收益增量比优化目标,设计了两阶段迭代求解优化算法。最后,通过中国北方某大型风电基地实际数据,对基准规划场景进行了评估,分析了系统灵活性缺额问题,并采用所述模型对源荷储资源进行优化规划,讨论了储能和需求侧响应在未来规划中的应用。算例表明,所提出的灵活性协调优化方法能够将灵活性量化评价指标纳入到电力系统规划中,优化得到不同约束阈值下的最优方案,能够快速进行参数灵敏度分析,从而提高优化方案的鲁棒性和适用性。

广义灵活电源; 源荷储一体化; 双层统筹规划; 高比例可再生能源; 净收益增量比

0 引言

灵活性资源规划对实现未来高比例可再生能源电力系统具有重要意义[1-3]。在传统电力系统中,灵活性资源主要依靠常规电源提供。但随着可再生能源电源比例大幅提高,常规电源容量进一步降低,仅靠常规电源提供灵活性不经济且技术不可行,逐渐减少的灵活性资源与增加的灵活性需求之间的矛盾凸显[4],因此需要充分挖掘系统源网荷储各个环节的灵活性资源潜力并对其进行统筹规划[5]。

灵活性规划是传统电力系统规划的扩展和优化,是针对系统不确定性特性及应对方案的专项规划。在低比例可再生能源系统中,系统不确定性较小,采用确定性的备用容量法即可以包络系统不确定性[6];随着可再生能源比例的增加,传统资源灵活性已经无法满足需求,已有研究在规划中考虑风电波动性和不确定性对规划方案的影响[7-8]。在灵活性规划方面,已有研究针对某一特定灵活性资源,如灵活机组[9]、储能[10]、需求侧响应[11-12]等进行规划。

纵观现有研究,仍然将传统电源规划与配电网资源(储能、需求响应)规划独立进行。然而,传统电源规划仅仅考虑留出备用裕度来提供灵活性,对于未来高比例可再生能源适应性不足,且定性方式容易带来规划方案的保守性和资源浪费。更加科学的方式是对源网荷储各环节资源建立定量的一体化统筹规划模型,从单一灵活性资源规划到多种资源潜力的全面综合利用,从而释放结果的保守性,达到成本效益的最佳平衡。

在源网荷储协同优化方面,已有研究进行了初步探索。文献[13]考虑热电系统,建立了多类灵活资源参与提高风电消纳的运行优化模型。文献[14]提出了同时考虑源荷储环节的优化调度模型。文献[15]提出了考虑需求侧资源的源网荷储协调优化调度模型。文献[16]提出了配电网层面源网荷协调的实时平衡调度模型。在规划领域,文献[17]提出源网荷协同规划的概念与模型,将能效电厂纳入电源规划。现有研究在规划阶段对于不确定性的处理,仍然采用传统的定性模式,缺乏灵活性需求和供给的定量化表示,难以准确回答灵活性资源是否充裕和最优规划容量的问题。其次,对于新能源出力的时序波动性和不确定性模拟,多以典型场景测算校验为主[18],模型的通用性较差;部分文献考虑详细的时序生产模拟模型[19-20],但是存在计算速度较慢的问题,难以纳入最优优化模型中考虑;也有文献不考虑详细的生产模拟[21],但是会忽略负荷及可再生能源的时序波动特性。

文献[22]提出了电力系统灵活性供需平衡机理及定量评价体系,从机理上阐述清楚了灵活性相关概念,并基于概率论建立了统一的数学框架。本文在此基础上,提出广义灵活电源的概念,即电力系统各环节能够提供灵活性的资源总称,并建立其双层统筹规划模型。通过该模型,在规划阶段充分挖掘系统各环节的调节潜力,参与到系统平衡中,从而弥补传统规划对系统灵活性需求考虑的不足。

本文主要围绕源荷储环节的灵活性优化规划开展,电网则作为支撑平台纳入约束考虑。首先,给出了电力系统源荷储一体化优化规划的思路,提出了广义灵活电源概念并对其特性进行了分析,简要介绍了灵活性规划的基础数学模型:生产模拟及灵活性评估。其次,提出了广义灵活电源协调优化的双层模型,证明了模型为凸规划。然后,基于最大净收益增量比算法提出了灵活性优化规划模型的两阶段算法。最后,基于实际系统对本文提出的模型进行了测算和验证。

1 广义灵活电源统筹优化规划的相关概念

1.1 广义灵活电源及灵活性供给的概念

本文基于文献[22]提出的电力系统灵活性定义,定义广义灵活电源如下:在给定时间尺度下,源、荷、储环节能够提供一定调节容量来适应电力系统随机变化的资源集合。与传统电源的概念不同,灵活电源提供的是灵活性而非电力,而广义则指源、荷、储多环节资源均可作为灵活电源。

灵活性供给指灵活电源在给定时间尺度下的调节能力,按照量纲的不同可分为爬坡型、功率型和能量型三类指标。爬坡型和功率型指标分别指该设备每分钟爬坡功率和功率调节范围占额定功率比例,而能量型指标与时间尺度相关,即功率型指标在给定时间尺度内的积分,不同环节各类灵活电源的调节能力参见附录A表A1。

广义灵活电源灵活性供给特性如图1所示。图中:Pg,Pst,PLi分别为机组出力、储能出力和负荷i水平；下标max和min分别表示上、下限值；yi(i=1,2,…,m)为场景i下的上调灵活性需求。图1(a)(b)右边的子图分别为电源和储能上、下调功率型灵活性供给随时间尺度的变化趋势,电源随时间尺度增加呈现饱和趋势,储能由于能量限制,在长时间尺度无法提供灵活性;左边的子图展示了在给定时间尺度下,其上调灵活性与设备出力状态的函数关系。以常规电源为例,在低出力阶段,其上调灵活性供给受爬坡约束为一常数,随着出力的进一步增加,上调灵活性供给降低。

图1(c)右边的子图描述了负荷带来的灵活性需求在不同时间尺度的变化规律,左边的子图描述了上调灵活性需求与负荷水平的关系,随着负荷水平的增加,上调灵活性需求减少。由于负荷变化存在不确定性,因此相应的曲线均有多条,每条曲线对应某一确切概率。

图1 源荷储灵活性资源多时间尺度调节特性Fig.1 Multiple time scale regulating characteristics for flexible resource in generation-load-storage

根据上述原理可知,电源、储能及负荷的灵活性供给或需求具有多时间尺度特性和状态相依特性,给定时间尺度和系统状态,则电源、储能及负荷环节资源的灵活性供给概率分布可参考文献[22]。

(1)

式中：Ss为灵活性供给源集合;A为灵活性方向,A∈{+,-}。

1.2 灵活性需求及裕量的数学模型

(2)

式中:D为灵活性需求源集合。

(3)

式中:Cmax和Cmin分别为条件参数上、下限;f(·)为概率密度函数。

1.3 广义灵活电源规划定义及其数学模型

灵活性规划定位是优化规划,即对基础规划方案的扩展及优化,是针对系统不确定性特性及应对方案的专项规划。本文基于灵活性平衡概念[22],对广义灵活电源规划定义如下:根据规划期负荷需求预测及传统规划方案Ω*,在满足系统灵活性水平的条件下,寻求经济性最优的广义灵活电源配置方案。

由于灵活性需求和供给源均具有不确定性和状态相依性,需要采用随机变量对其描述。因此,灵活性规划的约束方程和目标函数中均含有随机变量,其数学模型如式(4)所示,属于随机规划模型。

(4)

式中:X为灵活性资源投资决策变量;ξ和η分别为生产模拟中的待优化随机变量;c(·)为成本函数;f(·),gi(·),hj(·)为系统相关约束与决策变量间关系函数;M1和N1分别为不等式约束和等式约束的个数;P(·)和E(·)分别为求概率函数和求期望值函数。

本文选取灵活性不足概率和期望作为灵活性指标,其定义为:

(5)

(6)

可以看出,一旦系统边界条件集合Ω*以及优化模型确定,系统的灵活性指标为决策向量X的多元函数,即灵活性指标函数:

(7)

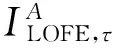
(8)

源荷储资源模型在灵活性平衡机理下具有统一性,不同环节的灵活性供需也具有相互转换特性,因此,为了得到最优规划方案,必须将此三者放入统一数学框架进行描述,进行一体化统筹规划,而电网作为灵活性资源传输的物理支撑平台,需要作为约束纳入考虑。本文中,“统筹”的内涵指在规划模型中,横向上考虑了多环节灵活性资源在不同时间尺度上的协调,纵向则实现了源荷储多类型资源的互补,从而能够从全局对资源配置进行优化决策。

2 广义灵活电源双层统筹优化规划模型

2.1 总体建模思路

如何在广义灵活电源优化规划模型中考虑灵活性指标约束,是本文建模的重点。从数学角度分析,灵活性、充裕性指标与系统决策变量之间呈现复杂的非线性关系,因此,灵活性平衡约束的加入使得规划问题成为高维度、非线性随机优化问题,在数学上具有较高的求解难度。

本文建立的灵活性规划模型采用双层协调规划方式,将其分解为灵活电源投资决策问题和运行模拟两个子问题,如附录A图A1和图A2所示。投资决策模型对灵活发电厂、储能、需求侧响应等灵活电源进行优化。生产模拟优化模型对目标年内系统电力、热力进行优化生产,输出各类资源的电力、热力生产情况。

在传统规划方案基础上,上层投资决策问题对源(深度调峰)、荷(需求响应)、储(储热、储能)等资源容量进行优化,得到方案。通过生产模拟优化模块得到净收益,并为灵活性评估模块输入系统运行点,计算系统灵活性指标,并反馈至上层投资决策模块,进行迭代优化。

双层优化规划的一般数学模型为:

(9)

s.t.h(xt)=0

(10)

g(xt)≤0

(11)

(12)

式中:t=1,2,…,T;F(·)和f1(·)分别为规划期内的总成本和单位时间的运行成本函数;CI为规划期t的总投资成本;CO为规划期t的总运行成本;xt和ut分别为规划期t的投资决策变量向量和运行变量向量;h(·)和g(·)分别为等式约束和不等式约束函数;T为规划周期长度,本文取8 760。

2.2 优化规划的数学模型

根据上述思路,灵活性规划问题可以分解为上层投资决策和下层运行模拟两个子问题,本节分别对其数学模型进行介绍。为了简化问题,本文先讨论单目标年的规划模型,多目标年的动态规划模型是后续的研究方向。

本文优化模型中,各类资源出力、灵活性供给和需求均采用随机变量描述,通过两层优化问题的交替迭代处理概率约束。对于下层运行模拟模型,采用文献[23]提出的机组安排策略,获取各类资源出力的概率分布,在此基础上进行概率卷和/卷差运算,计算得到灵活性指标,反馈到上层优化模型中,进行约束条件校验。

2.2.1上层问题:广义灵活电源投资决策模型

上层问题的优化目标为最大化系统总净收益增量。净收益增量为与规划前相比,系统的净收益变化与灵活性资源投资成本之差,如式(13)所示。

(ϖg+ϖc+ϖp)Δfgi(p|X,λi,μj)dp-

(13)

式中:ΔBκ(X)和ΔCκ(X)分别为资源κ在规划方案X下相对于规划前的效益变化和成本变化,从全系统角度看,系统净收益增加等于火电机组发电量降低带来的煤耗和碳排放成本降低、可再生能源出力增加效益,其中,下标κ表示灵活性资源类型,可取为g,st,dr,分别表示电源、储能及需求侧灵活性资源;ϖg,ϖc,ϖp分别为煤价、碳排放价及可再生能源单位收益;w为贴现率;Nμ和Nλ分别为条件参数μj和λi的数量;Ng为机组数量;fgi(·)为煤耗特性函数;Pgi,max为最大机组出力;Δfgi(·)为规划后机组出力概率密度与规划前的差值;LT为设备寿命周期;ci为设备i的单位投资成本。

约束条件为多时间尺度各方向灵活性水平约束和灵活电源投资约束等,其数学模型如式(14)所示。其中,第1个约束阐述了各类资源出力向灵活性供给的转化过程,第2个约束为灵活性裕量分布的计算公式,第3和第4个约束分别为灵活性概率和期望约束,第5和第6个约束为灵活性资源投资容量约束。

(14)

2.2.2下层问题:非时序概率运行校验模型

下层问题基于非时序模拟模型[22],以最大化可再生能源消纳为目标,约束条件为系统网络及电、热平衡约束,各类机组及灵活电源特性约束,获取系统运行状态的概率分布,其数学模型如式(15)所示。

(15)

式(15)属于泛函极值模型,决策变量为各类型常规机组出力累积分布函数Fi和概率密度函数fi,i=1,2,…,N;热电联产机组热功率累积分布函数Gi和概率密度函数gi,i=1,2,…,M,其中M为热电联产机组数量;可再生能源出力累积分布函数Fre,i和概率密度函数fre,i,i=1,2,…,Nre;灵活性资源出力累积分布函数Fxi和概率密度函数fxi,i=1,2,…,n。基于上述计算结果,采用1.1节和1.2节介绍的方法即能够进行灵活性评估。

2.3 模型最优解的存在性证明

借助灵活性指标函数的概念,可将上述双层模型转化为单层优化模型,如式(16)所示。

(16)

本节对上述模型最优解的存在性和唯一性进行证明,首先介绍相关的几个概念。

1)定义:最优搜索轨迹

(17)

2)推论:灵活性指标函数具有边际递增性和凸性

(18)

取任意两点∀s1≤s2(s1,s2∈S*),取λ∈[0,1],令s=λs1+(1-λ)s2,根据灵活性函数的性质,可得到如下关系:

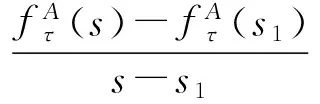
(19)

整理即得到:

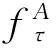
(20)

(21)

在上述单层优化问题中,如果沿最优搜索轨迹增加灵活性资源,根据实际工程的物理意义,总可寻找到灵活性资源配置满足罚函数为0。随着投资成本的增加,系统的净收益增量呈现先增后减的趋势,因此存在资源配置的局部成本最优值。下面证明最优值的全局最优性。

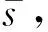
对于任意的s∈S*,有由于目标函数为凸函数[24],则式(22)成立。

(22)

3 模型求解

根据上文分析可知,系统灵活性指标依赖于决策变量(灵活性资源容量配置),且二者间不存在明确的解析函数形式。因此模型的求解难点在于如何在上层灵活性资源优化决策模型中考虑灵活性指标评价。有两个思路可解决上述问题。

1)通过大量仿真,研究灵活性指标与决策变量的近似函数关系,并进行拟合,得到多元线性或二次拟合解析式,并将其纳入灵活性优化规划模型中进行求解。

2)迭代求解。依据单位改善效果成本最低的原则增加灵活性资源,并计算灵活性指标判断是否满足需求,如果不满足继续按照上述原则进行迭代计算。

本文提出最大净收益增量比算法来求解灵活性优化规划模型,其中净收益微增率定义为增加单位灵活性付出的总成本,如式(23)所示。

(23)

由于灵活性机组同时在电力电量平衡约束和灵活性约束中,属于耦合变量。本文采用两阶段法进行求解,第一阶段不考虑上层投资决策模块,直接给出初始解,并进行生产模拟优化。第二阶段以该解为初始点,根据最大净收益增量比算法,进行迭代计算,获取最优灵活性资源配置。设当前在第k步迭代,则选取增加的灵活性资源类型按照式(24)确定。

(24)

式中:Di为优化模型可行域。

系统灵活性资源决策变量及总成本按照式(25)进行调整。

(25)

计算系统灵活性指标,如果不满足式(14)中的灵活性约束,令k=k+1,继续按照上述过程进行迭代计算;否则达到最优解,迭代结束。

根据灵活性电源最优数量,对传统电源规划结果进行调整,按照成本从高到低顺序,降低传统非灵活电源数量。详细两阶段算法流程参见附录A图A3。

4 算例分析

4.1 算例系统介绍

本文以中国北部某区域电网的历史预测、实测数据和电源结构等数据为基础,采用本文提出的灵活性定量评估模型和指标进行量化分析,主要研究以下内容:①系统规划年生产模拟及灵活性评估,分析基准情况下系统各环节的成本效益情况;②不同灵活性资源对系统成本效益的影响,并进行灵敏度分析;③目标年的最优灵活性投资规划方案;④各类参数对最优投资方案的影响。

本文算例系统目标年的可再生能源装机规划容量如下:风电装机容量为24 000 MW,光伏装机容量为6 460 MW,水电装机容量为540 MW,含水电可再生能源装机容量占负荷峰值64%,属于高比例可再生能源系统。研究时段内的最大负荷为48 400 MW,最小负荷为34 130 MW。该地区规划期电力供暖面积达2.025×108m2。仿真系统电网规划年拓扑图见图2,某典型仿真日系统电热负荷及可再生能源曲线和相关参数参见附录B图B1和表B1至表B3。

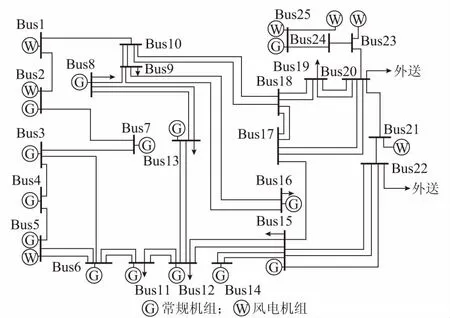
图2 仿真系统电网拓扑图Fig.2 Power grid topology diagram of simulation system

4.2 基准场景方案分析

根据算例系统的规划年的边界条件,进行生产模拟和灵活性评估,得到多时间尺度灵活性评价结果(0.25～24 h)、失负荷及可再生能源限电数据,如表1所示。表中:LOFP表示灵活性不足概率;LOFE表示灵活性不足期望。

表1 目标年灵活性评价结果及限电量分析Table 1 Flexibility assessment results and limited power analysis in planning year

通过表1可知,系统在各时间尺度的上调灵活性不足概率及期望较低,而相应下调指标较高,说明系统主要存在下调灵活性缺额,从而造成严重的再生能源限电现象。本文以上述成本数据作为基准点,考虑源荷储各环节的灵活性资源,以最大化净收益的轨迹进行优化规划。

4.3 规划方案下的最优灵活性投资方案

本节分别考虑电源(火电机组深度调峰)、负荷(需求侧响应)、储能(储热或储电)三类灵活性资源,需求侧响应考虑分时电价模型(TOU)。根据最大净收益增量比算法,灵活资源总容量从0至10 000 MW,选取步长500 MW,逐点计算灵活性资源的最优搜索轨迹,在此基础上,基于成本效益法分析不同灵活性指标阈值下的最优灵活性规划方案。在灵活性资源的最优搜索轨迹下,系统收益、投资成本及净收益与规划容量的关系如图3所示。

图3 收益、成本、净收益及灵活性指标与规划容量关系Fig.3 Relationship between benefit, cost, net benefit, flexibility index and planning capacity

图3同时给出了系统最优规划轨迹下的净收益曲线和制约灵活性指标变化曲线,两者结合可获取系统在满足灵活性要求下的最优灵活性资源投资决策方案。以灵活性约束为0.05为例,其对应的灵活性投资容量约为4 000 MW,即在横坐标不小于该值的范围内寻找净收益曲线最优值,可以看出最优投资容量为4 500 MW;如果灵活性约束为0.025,则对应的灵活性容量约为6 250 MW,此时净收益曲线开始递减,因此最优投资容量即为6 250 MW。考虑灵活性约束阈值分别为0.1,0.05,0.025,0.01,不同场景下各环节资源的最优投资方案如表2所示。

表2 不同灵活性阈值下的最优投资容量Table 2 Optimal planning capacity under different flexibility thresholds

由表2可知,不同阈值对最优热电调峰容量影响较小,主要原因是该资源的规划效益最高;阈值高于0.05时,系统仅通过热电机组调峰即可满足灵活性需求;阈值低于0.025时,需要增加储能、需求侧响应资源,并通过自备电厂调峰提供灵活性。规划前后系统多时间尺度灵活性不足概率如表3所示,可以看出本文的优化模型能够满足不同时间尺度的灵活性水平要求。

表3 规划前后多时间尺度灵活性指标对比Table 3 Comparison of multi-time flexibility indices before and after planning

规划模型同时可得到电网各节点灵活性资源最优配置,参见附录B图B2。可以看出,热电深度调峰机组主要集中在节点12,15,22,其次是节点2,4,5,而自备调峰机组主要集中在节点11,12,14;储能分布较为分散,主要集中在节点9至14及节点21和22,这几个节点的负荷较大,充分体现了储能与负荷的互补优势;需求侧响应则主要在节点8和9。

4.4 最优规划方案的灵敏度分析

最优规划方案与各类参数取值相关,在规划阶段各类参数具有一定不确定性,因此需要进行灵敏度分析。本节主要讨论以下几个方面的灵敏度分析:①灵活性不足惩罚因子;②储能投资成本;③可再生能源接入比例;④需求侧响应参与比例。

4.4.1灵活性不足惩罚因子

上述分析均是在不考虑灵活性不足惩罚因子的情况下进行的,本小节在净收益函数中增加灵活性不足惩罚项,分别考虑惩罚项为基准值的50%,75%,100%和125%这4个场景,系统最优净收益增量轨迹与灵活性投资容量的关系,如附录B图B3所示。

可以看出,随着惩罚因子的增加,系统灵活性资源最优投资容量轨迹向右偏移,即最优规划容量增加。原因分析如下:如果灵活性不足的惩罚项在总成本中权重增加,则灵活性不足带来的惩罚成本较高,因此投资更多灵活性资源会降低这部分成本,从而提高总的净收益,因此最优规划容量增加。

4.4.2可再生能源接入比例

本小节研究可再生能源接入比例对系统灵活性规划结论的影响。设灵活性约束阈值为0.025,分别计算可再生能源基准场景、装机容量的1.25倍、装机容量的1.5倍、装机容量的1.75倍、装机容量的2倍5个场景下的最优灵活性资源规划方案,计算结果如附录B图B4所示。

可以看出,主要靠热电调峰提供灵活性,储能和需求侧响应容量较少。随着可再生能源比例的增加,热电和自备调峰容量基本呈现线性增加,而储能由于成本较高,在较高可再生能源比例下才具有技术经济性。需求侧响应由于对灵活性的调节能力有限,增加比例并不明显。

4.4.3储能投资成本

根据预测,储能成本在2020,2025,2030年分别下降30%,60%,70%。分别计算各目标年下储能的最优配置容量,考虑未来可再生能源装机翻倍场景,计算结果如附录B表B4所示。

可以看出,随着储能LCOE的下降,其最优投资容量呈现上升趋势,且与灵活性指标阈值有较强关系。在低灵活性阈值下,储能最优容量较低,即较少的储能投资即可满足系统灵活性要求;在高灵活性阈值下,储能最优容量增加。例如在2030年,如果阈值从0.1降低到0.05,最优储能容量从4 000 MW增加到10 000 MW。

4.4.4需求侧资源

需求侧响应能够以较低成本提供灵活性,但由于需求侧弹性的限制,实际需求侧参与比例较低(不足2%)。在未来电力系统中,如果充分挖掘和释放需求侧的弹性,则需求侧响应参与比例可大大提高。本节分别讨论需求侧响应参与比例潜力从0增加至8.26%,实际最优需求侧响应的最佳参与比例,计算结果如附录B图B5所示,其中S1和S2分别对应基准场景和可再生能源装机容量翻倍场景。

可以看出,随着需求侧响应参与潜力的增加,实际最优响应容量先呈现增加趋势,然后趋于饱和。对于场景S1和S2,最优需求响应参与容量分别是1 500 MW(对应比例3.1%)和2 500 MW(对应比例5.2%),说明需求响应容量并不是越高越好,存在一个技术经济最优值。

5 结语

将灵活性定量评价纳入电力系统规划是实现高比例可再生能源并网的重要基础。本文对电力系统灵活性规划的定义、特征及协调优化的一般数学形式进行了阐述,分析了源荷储多元灵活性资源一体化协调优化思路,提出了含灵活性资源投资决策层和运行模拟层的双层统筹规划框架,揭示了电力系统灵活性规划的协调机理。

本文基于非时序生产模拟和灵活性评估模型,建立了考虑电网约束的详细灵活性规划数学模型,证明了模型的凸性,并提出了基于最大净收益微增率的两阶段求解算法,实现了系统在灵活性约束下的最优资源投资决策。

仿真分析表明,本文提出的灵活性协调优化方法能够将灵活性量化评价指标纳入到电力系统规划中,能够优化得到不同约束阈值下的最优方案。本文模型能够快速进行参数灵敏度分析,从而提高优化方案的鲁棒性和适用性。

由于模型复杂度的限制,本文仅考虑了电力系统源荷储环节的灵活性资源类型,电网灵活性资源暂未考虑。源荷储资源协调优化是灵活性规划的第一步,本文未来研究方向之一是在此基础上,研究如何通过优化电网结构降低灵活性资源投资量,研究方向之二是研究灵活性资源的市场激励模型。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] International Energy Agency. The power of transformation: wind, sun and the economics of flexible power systems[R]. 2013.

[2] North American Electric Reliability Corporation. Special report: accommodating high levels of variable Generation[R]. 2009.

[3] 国家发展和改革委员会能源研究所.中国2050高比例可再生能源发展情景暨路径研究[R].2015.

[4] PAPAEFTHYMIOU G, GRAVE K, DRAGOON K. Flexibility options in electricity systems[R]. 2014.

[5] 鲁宗相,李海波,乔颖.含高比例可再生能源电力系统灵活性规划及挑战[J].电力系统自动化,2016,40(13):147-158.DOI:10.7500/AEPS20151215008.

LU Zongxiang, LI Haibo, QIAO Ying. Power system flexibility planning and challenges considering high proportion of renewable energy[J]. Automation of Electric Power Systems, 2016, 40(13): 147-158. DOI: 10.7500/AEPS20151215008.

[6] 王锡凡.电力系统优化规划[M].北京:水利电力出版社,1990.

[7] 张节潭,苗淼,范宏,等.含风电场的双层电源规划[J].电网技术,2011,35(11):43-49.

ZHANG Jietan, MIAO Miao, FAN Hong, et al. Bi-level generation expansion planning with large-scale wind farms[J]. Power System Technology, 2011, 35(11): 43-49.

[8] 穆永铮,鲁宗相,周勤勇,等.基于可靠性均衡优化的含风电电网协调规划[J].电网技术,2015,39(1):16-22.

MU Yongzheng, LU Zongxiang, ZHOU Qinyong, et al. Optimized reliability balancing based transmission coordinating expansion planning for power grid with wind farms[J]. Power System Technology, 2015, 39(1): 16-22.

[9] MA J, SILVA V, BELHOMME R, et al. Evaluating and planning flexibility in sustainable power systems[J]. IEEE Trans on Sustainable Energy, 2013, 4(1): 200-209.

[10] 陆秋瑜,胡伟,闵勇,等.考虑时间相关性的风储系统多模式协调优化策略[J].电力系统自动化,2015,39(2):6-12.DOI:10.7500/AEPS20140922004.

LU Qiuyu, HU Wei, MIN Yong, et al. A multi-pattern coordinated optimization strategy of wind power and energy storage system considering temporal dependence[J]. Automation of Electric Power Systems, 2015, 39(2): 6-12.DOI: 10.7500/AEPS20140922004.

[11] ZENG Bo, ZHANG Jianhua, YANG Xu, et al. Integrated planning for transition to low-carbon distribution system with renewable energy generation and demand response[J]. IEEE Trans on Power Systems, 2014, 29(3): 1153-1165.

[12] 曾鸣,杨雍琦,向红伟,等.计及需求侧响应的电力系统鲁棒优化规划模型[J].电力系统自动化,2016,40(17):137-145.DOI:10.7500/AEPS20150615001.

ZENG Ming, YANG Yongqi, XIANG Hongwei, et al. Robust optimization planning model of power system considering demand response[J]. Automation of Electric Power Systems, 2016, 40(17): 137-145. DOI: 10.7500/AEPS20150615001.

[13] 凡鹏飞,张粒子,谢国辉.充裕性资源协同参与系统调节的风电消纳能力分析模型[J].电网技术,2012,36(5):51-57.

FAN Pengfei, ZHANG Lizi, XIE Guohui. Analysis model for accommodation capability of wind power with adequacy resources involved in system regulation[J]. Power System Technology, 2012, 36(5): 51-57.

[14] 宋艺航,谭忠富,李欢欢,等.促进风电消纳的发电侧、储能及需求侧联合优化模型[J].电网技术,2014,38(3):610-615.

SONG Yihang, TAN Zhongfu, LI Huanhuan, et al. An optimization model combining generation side and energy storage system with demand side to promote accommodation of wind power[J]. Power System Technology, 2014, 38(3): 610-615.

[15] 曾鸣,杨雍琦,向红伟,等.兼容需求侧资源的“源-网-荷-储”协调优化调度模型[J].电力自动化设备,2016,36(2):102-111.

ZENG Ming, YANG Yongqi, XIANG Hongwei, et al. Optimal dispatch model based on coordination between “generation-grid-load-energy storage” and demand-side resource[J]. Electric Power Automation Equipment, 2016, 36(2): 102-111.

[16] 朱建全,段翩,刘明波.计及风险与源-网-荷双层协调的电力实时平衡调度[J].中国电机工程学报,2015,35(13):3239-3247.

ZHU Jianquan, DUAN Pian, LIU Mingbo. Electric real-time balance dispatch via bi-level coordination of source-grid-load of power system with risk[J]. Proceedings of the CSEE, 2015, 35(13): 3239-3247.

[17] 张宁,胡兆光,周渝慧,等.计及随机模糊双重不确定性的源网荷协同规划模型[J].电力系统自动化,2016,40(1):39-44.DOI:10.7500/AEPS20150607002.

ZHANG Ning, HU Zhaoguang, ZHOU Yuhui, et al. Source-grid-load coordinated planning model considering randomness and fuzziness[J]. Automation of Electric Power Systems, 2016, 40(1): 39-44. DOI: 10.7500/AEPS20150607002.

[18] 段建民,王志新,王承民,等.考虑碳减排效益的可再生电源规划[J].电网技术,2015,39(1):11-15.

DUAN Jianmin, WANG Zhixin, WANG Chengmin, et al. Renewable power planning considering carbon emission reduction benefits[J]. Power System Technology, 2015, 39(1): 11-15.

[19] PALMINTIER B S, WEBSTER M D. Impact of operational flexibility on electricity generation planning with renewable and carbon targets[J]. IEEE Trans on Sustainable Energy, 2016, 7(2): 672-684.

[20] BELDERBOS A, DELARUE E. Accounting for flexibility in power system planning with renewables[J]. International Journal of Electrical Power & Energy Systems, 2015, 71: 33-41.

[21] MEJIA-GIRALDO D, MCCALLEY J D. Maximizing future flexibility in electric generation portfolios[J]. IEEE Trans on Power Systems, 2014, 29(1): 279-288.

[22] 鲁宗相,李海波,乔颖.高比例可再生能源并网的电力系统灵活性评价与平衡机理[J].中国电机工程学报,2017,37(1):9-19.

LU Zongxiang, LI Haibo, QIAO Ying. Flexibility evaluation and supply/demand balance principle of power system with high-penetration renewable electricity[J]. Proceedings of the CSEE, 2017, 37(1): 9-19.

[23] 王晓海,乔颖,鲁宗相,等.供暖季风电电量消纳能力的评估新方法[J].中国电机工程学报,2015,35(9):2112-2119.

WANG Xiaohai, QIAO Ying, LU Zongxiang, et al. A novel method to assess wind energy usage in the heat-supplied season[J]. Proceedings of the CSEE, 2015, 35(9): 2112-2119.

[24] 陈宝林.最优化理论与算法[M].北京:清华大学出版社,2005.

李海波(1990—),男,通信作者，博士研究生,主要研究方向:可再生能源并网的风险/可靠性及灵活性评估、分布式电源规划与运行、分布式储能优化运行、电动汽车。E-mail： li-hb12@mails.tsinghua.edu.cn鲁宗相(1974—),男,博士,副教授,主要研究方向:风电/太阳能发电并网分析与控制、能源与电力宏观规划、电力系统可靠性、分布式电源及微电网。E-mail: luzongxiang98@tsinghua.edu.cn

乔 颖(1981—),女,博士,副教授,主要研究方向:新能源、分布式发电、电力系统安全与控制。E-mail: qiaoying@tsinghua.edu.cn

(编辑万志超)

Bi-levelOptimalPlanningofGeneration-Load-StorageIntegratedGeneralizedFlexibilityResource

LIHaibo1,2,3,LUZongxiang1,2,QIAOYing1,2

(1. Department of Electrical Engineering, Tsinghua University, Beijing 100084, China; 2. State Key Laboratory of Control and Simulation of Power System and Generation Equipments, Tsinghua University, Beijing 100084, China; 3. Tsinghua Sichuan Energy Internet Research Institute, Chengdu 610200, China)

In power systems with high penetration renewable energy, the contradiction between the reduced conventional flexible generation resource and the increased flexibility demand is becoming increasingly serious. According to the flexibility balance principle, the concept of generalized flexibility is proposed and the bi-level optimal planning model including investment decision and production simulation verification is developed. Then the convexity of the planning model is proved and a two stage algorithm proposed based on the maximum net benefit/increment ratio. Finally, through the actual data of a large wind power base in north China, the benchmark scenario is evaluated, and the problem of system flexibility deficiency is analyzed. Meanwhile, the optimal planning for generation-load-storage source is implemented by the proposed model, and the sensitivity analysis for storage and demand response is discussed. The case study indicates that the proposed method can integrate the flexibility assessment in power system planning, which can also quickly conduct the sensitivity analysis to improve the robustness and applicability.

This work is supported by National Key Research and Development Program of China (No. 2016YFB0900100), National Natural Science Foundation of China (No. 51677099) and State Grid Corporation of China (No. SGGSKY00FJJS1600209).

generalized flexibility resource; generation-load-storage integration; bi-level optimal planning; high penetration of renewable energy; net benefit/increment ratio

2017-02-05;

2017-08-22。

上网日期: 2017-09-22。

国家重点研发计划资助项目(2016YFB0900100);国家自然科学基金资助项目(51677099);国家电网公司科技项目(SGGSKY00FJJS1600209)。