基于Benders分解的独立型微电网鲁棒优化容量配置模型

刘思夷, 赵 波, 汪湘晋, 邱海峰, 林湘宁

(1. 强电磁工程与新技术国家重点实验室(华中科技大学), 湖北省武汉市 430074; 2. 国网浙江省电力公司电力科学研究院, 浙江省杭州市 310014)

基于Benders分解的独立型微电网鲁棒优化容量配置模型

刘思夷1, 赵 波2, 汪湘晋2, 邱海峰2, 林湘宁1

(1. 强电磁工程与新技术国家重点实验室(华中科技大学), 湖北省武汉市 430074; 2. 国网浙江省电力公司电力科学研究院, 浙江省杭州市 310014)

为了提高独立型微电网电源优化配置的鲁棒性,综合考虑了风、光和负荷的间歇性和随机性,建立了独立型微电网的双层鲁棒优化容量配置模型。外层为初始投资费用主问题,内层为基于风、光和负荷不确定集的运行优化子问题。采用对偶的方法对子问题进行解耦,利用大M法将其线性化,并通过Benders分解的方法将主子问题进行交互迭代,直至经济成本达到最优。在算例中将该方法与改进的非支配排序遗传算法(NSGA-Ⅱ)进行对比,结果表明所提模型的鲁棒性更好,求解效率更高,验证了模型的合理性和有效性。

微电网(微网); 优化配置; 鲁棒优化; Benders分解; 不确定集

0 引言

微电网由于能够灵活接入分布式电源,其应用得到了广泛关注。目前在一些偏远山区和远离城市的海岛,由于很难建立与大电网的互联,在这些地区建立供电可靠的独立型微电网是有效利用当地可再生资源、解决电力不足、减少环境污染的有效方法[1]。

分布式电源的优化配置是微电网规划的主要前期工作,其涉及电源容量配置和运行优化的耦合性,解决该类问题的一种途径是将电源容量和运行变量联合建模优化。文献[2]采用枚举法联立求解所有可能机组台数和运行变量的组合方案,但存在解空间大、求解时间较长的缺点。另一种途径是将问题分为两层交互求解,外层为容量配置问题,内层为运行优化问题。文献[3]基于粒子群算法,以电网等年值费用最低为目标,对风/光/储独立型供电系统优化配置问题进行了求解;文献[4]采用改进细菌觅食算法以系统的经济性为目标函数,求解了风/光/储独立型微电网的优化配置问题。

以上方法都是基于智能算法的启发式随机搜索算法,该类算法通常需要大量初始种群,不能保证找到全局最优解。同时,以上方法均没有充分考虑容量配置和运行优化的耦合性,不能较好体现运行优化对容量配置的影响。

此外,由于风、光资源和负荷具有较强的间歇性和波动性,会影响微电网优化配置的经济性和可靠性,因此应充分考虑其不确定性因素的影响。减小不确定性因素影响的方法有引入储能系统和负荷侧响应。文献[5]研究了引入电动汽车和水泵储水系统以应对独立储能系统的可再生能源的波动性;文献[6]考虑引入负荷侧响应来减小大规模风电并网不确定性的影响。针对微电网中不确定因素影响的研究方法主要有如下三种。

1)基于历史数据的序贯仿真方法。文献[7]利用确定的数据序贯仿真模拟风、光出力,建立了考虑电网经济性和可靠性的微电网优化配置模型。但基于历史数据的序贯仿真方法不能很好地体现不确定性对系统鲁棒性的影响。

2)基于概率论的随机规划方法。文献[8]考虑系统的不确定因素,采用随机机会约束规划方法。文献[9]采用拉丁超立方抽样生成风电场景并进行缩减。基于概率论的随机规划方法存在分布函数不能准确拟合的缺点,并且需要大量抽样以获得随机场景并进行场景缩减,增加了问题的复杂性。

3)鲁棒优化方法。文献[10]采用盒式集合表示风速的不确定性对并网型微电网的风机容量进行规划;文献[11]将鲁棒优化理论引入到电力系统优化调度中,构建了大规模间歇式电源接入的多目标鲁棒优化调度模型。由于鲁棒优化不需要获取不确定数据的概率分布,而是采用集合的方式表示不确定因素的取值范围[12]。因此采用鲁棒优化方法构建目标函数,有利于增强系统应对最恶劣自然条件时的性能,提高系统稳定性。

本文以包含风/光/柴/储的独立型微电网为研究对象,构建了考虑风、光出力和负荷不确定性的二层鲁棒优化混合整数规划模型。目标函数的外层为微电网的初始投资费用,内层为包含不确定集的微电网的运行费用、停电惩罚费用和弃电费用;采用Lagrange对偶方法将内层最小—最大鲁棒优化模型进行解耦,引入大M法将对偶问题线性化;用Benders分解的方法将外层问题和内层问题交互迭代求解直到目标函数达到最优。在算例分析中,将该模型与改进的非支配排序遗传算法(NSGA-Ⅱ)进行对比,验证了所提模型的合理性。

1 独立型交流微电网模型

本文采用的独立型微电网的拓扑结构如图1所示,其中蓄电池和光伏通过换流设备连接在交流母线上。微电网采用孤岛运行方式,依靠内部电源满足负荷供电需求。当风机和光伏发电过多或负荷较小时,微电网向储能充电,若储能容量达到上限则丢弃部分多余发电功率。当风电和光伏发电不足时,储能向负荷放电或者开启柴油发电机向负荷供电。若仍不能满足负荷需求,则切除部分负荷。

图1 独立型交流微电网结构Fig.1 Structure of stand-alone alternating current microgrid

2 微电源模型

2.1 风力发电模型

风机的发电功率由风机毂轮高度处的风速决定,用指数定律表达式对风速进行变换[13]。

(1)

式中:α为地表粗糙程度的描述因素,本文取值为0.22;vref(t)为测风点风速;Href为测风点高度;H为风机毂轮高度。

风机的输出特性曲线采用变浆距风机输出特性曲线[14],当风速小于切入风速vci时,风机发电功率为0;当风速大于切入风速vci小于额定风速vcr时,其输出功率Pr(v)由变浆距风机曲线拟合得到;当风速达到额定风速vcr小于切出风速vco时,风机以额定功率Pr运行;当风速大于切出风速vco时,风机停止运行,输出功率为0。

(2)

2.2 光伏发电模型

本文采用的光伏发电的输出功率模型为[15]:

(3)

式中:fpv为光伏阵列能量转换效率,本文取0.9;Prate为光伏阵列的额定功率;A为光伏的实际辐照度;As为光伏的额定辐照度;αp为功率温度系数,一般取-0.004 7 ℃-1;TSTC为标准测试条件下光伏组件的温度,一般取25 ℃;Tpv为光伏组件的实际温度。

2.3 柴油发电机模型

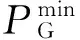
(4)

柴油发电机的耗油量V(t)与运行功率之间的关系为[16]:

(5)

式中:F0为柴油发电机燃料曲线的截距系数,即柴油机的空载油耗量;F1为柴油发电机燃料曲线的斜率。

2.4 储能模型

储能具有最大充放电功率限制,其最大充放电功率与电池额定容量Erate成正比,储能实际充放电功率Pbat(t)为正表示储能放电,若为负则表示储能充电:

-εErate≤Pbat(t)≤εErate

(6)

式中:ε为储能最大充放电功率与储能额定容量的比值。

储能的荷电状态与充放电功率的关系为:

(7)

式中:SSOC为储能的荷电状态;Pdch(t)为储能的放电功率;Δt为时间步长,本文取1 h;ηd为电能转化为放电功率的效率;Pch(t)为储能充电功率;ηc为储能的充电效率。

储能电池的荷电状态具有上下限,若荷电状态太低或太高都会缩短储能电池的使用寿命:

(8)

2.5 风、光出力及负荷的不确定集模型

由于在独立型微电网中风机和光伏发电的比例较大,而风速、光照强度和负荷通常具有间歇性、波动性和不可预测性,风机、光伏发电和负荷功率的大小会影响系统的运行状态,因此需考虑不确定因素对系统的影响。鲁棒优化采用集合的方式表示变量的不确定性,其关键在于不确定集的设计。根据长期统计信息,风机、光伏的输出功率和负荷的大小可以表示成在预测值附近上下浮动,浮动量由系统的不确定性决定。整个周期内扰动量的取值具有上下限值。不确定集的表示形式如式(9)所示。

(9)

3 优化配置模型的建立和求解算法

3.1 优化配置的目标函数

由于微电网电源容量配置在很大程度上受到运行优化的影响,在本质上是双层优化,并且要考虑风、光、负荷等不确定因素对系统稳定性的作用,因此可建立双层鲁棒优化容量配置模型,以提高系统的鲁棒性。双层鲁棒优化原问题的目标函数分为两层:外层为分布式电源的最小净现值投资成本,内层为包含风、光和负荷不确定集的运行费用、停电惩罚费用和弃电费用。内层运行成本的目标函数为在所有不确定集作用下使得目标函数尽可能大的情况下,在运行变量作用下使目标函数尽可能小,在数学上可表示带有约束的最小—最大鲁棒优化模型[17]。

Ctotal=minCint+min(maxCopt)

(10)

(11)

Copt=Cde+Clsh+Cdump=

(12)

3.2 广义Benders分解的基本原理

以上优化问题是一个典型的混合整数规划问题,适用于Benders分解的方法求解。Benders分解最开始用于求解混合整数规划问题,即实型变量和整型变量同时出现时的极值问题[18],其基本原理见附录A。

3.3 Benders分解流程

利用Benders分解原理求解微电网优化配置问题的基本原理见附录B图B1,求解步骤见附录B图B2。

求解过程中将原问题分解为主问题和子问题。主问题是以机组台数为决策变量的电源容量规划问题,变量类型为整型变量。子问题是以各机组出力、弃电量和切负荷量为决策变量的最优运行子问题,包含风、光出力和负荷的不确定集,变量类型为整型变量和实型变量。主问题初始化机组台数代入子问题,子问题首先进行可行性检验,判断主问题的决策变量是否能满足所有约束条件。若不能满足则返回不可行割,对主问题优化台数进行调整,直到满足所有约束条件为止。若主问题的决策变量能够满足所有约束条件,子问题进一步进行经济优化计算,向主问题返回该台数配置附近的边际增量信息(即对偶变量的大小),对主问题中的台数配置进行调整,直到找到最优解。采用Benders分解方法求解电源容量优化配置问题的具体步骤如下。

步骤1:初始化原问题的上界和下界。

步骤2:求解机组台数配置主问题,并更新原问题的下界。

步骤3:将主问题中求解得到的机组台数代入可行性检验子问题,判断该机组台数配置是否能够满足所有约束。若可行性检验问题中引入的松弛变量之和为零,说明问题可行,进行下一步。若松弛变量之和不为零,说明该机组台数配置不满足所有约束条件。则给主问题添加不可行割,返回步骤2重新求解主问题,对主问题的机组台数进行调整。

步骤4:若主问题初始化台数满足所有约束,则计算运行优化子问题的对偶问题,更新原问题的上界。

步骤5:若上界与下界的差小于阈值则说明原问题已经达到最优解。否则给主问题增加可行割,重新求解主问题,对机组台数进行调整。

子问题和主问题的数学形式如下。

1)可行性检验子问题的目标函数是为了满足所有约束条件引入的松弛变量之和最小,其在第w次迭代时的求解形式:

min(maxS)=S1+S2+S3

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

Plsh(t)≥0

(22)

Pdump(t)≥0

(23)

(24)

(25)

(26)

(27)

S1≥0

(28)

S2≥0

(29)

S3≥0

(30)

式(14)表示功率平衡约束;式(15)表示柴油发电机组的出力范围约束;式(16)为可再生能源机组的发电功率;式(17)至式(19)为储能约束,由于初始时刻储能的容量E0为常数而不是变量,所以单独列出;式(22)表示切负荷量大于等于零;式(23)表示弃电量大于等于零;式(24)表示全年切负荷不超过总负荷的比例,取值为μL;式(25)表示弃电量不超过总负荷的λ倍,否则会造成可再生能源的浪费;式(26)表示可再生能源功率渗透率要达到总负荷ζ倍;式(27)表明在一个运行周期后储能电池的容量保持在初值;式(28)至式(30)表示引入的对偶变量大于等于零。

2)经济最优运行子问题

经济最优运行子问题的目标函数为最大不确定性下的运行费用最小:

(31)

经济最优子问题的约束条件与可行性检验子问题相同,只是约束条件(式(24)至式(26))中不含有松弛变量。采用Lagrange对偶方法对最小—最大模型进行解耦,其对偶问题的目标函数为:

(32)

式中:yi为序号为i的约束条件引入的对偶变量。

原问题的上界为:

(33)

式中：Λ为运行优化子问题的目标函数值。

3)主问题第w次迭代时的求解形式为:

(34)

可行性检验子问题增加的不可行割为:

(35)

最优运行子问题增加的可行割为:

(36)

返回的可行割通过对偶变量来表示原问题的边际增量,调整后的机组台数决策变量能够得到更经济的运行子问题,给定原问题的下界为Z。

在求解子问题对偶问题的过程中,存在对偶变量与不确定集中0-1变量的乘积,采用大M法[19]将其线性化进行求解。

4 算例分析

本文采用实际风、光资源和负荷数据进行计算,其中风速、光照幅度和负荷曲线见附录B图B3,全年平均风速为5.70 m/s,负荷均值为73.16 kW,日平均辐照为3.07(kW·h)/m2。

系统的具体参数如下:全年切负荷率小于0.3%,弃电率小于分布式电源总发电量的10%,可再生能源功率渗透率大于等于70%。储能容量荷电状态初值为0.7,荷电状态的设定范围为[0.4,0.95],储能充放电效率为0.95。整个工程的寿命为20年,通货膨胀率为0.03,弃电费用为0.6元/kW,切负荷费用为1.3元/kW。分布式电源和储能的参数见附录B表B1和表B2。

4.1 不同不确定水平下优化配置结果的比较

对全年每个月构造典型日,采用每个月各时刻的平均值作为该月典型日预测值,即不考虑不确定性。此时,风、光发电及负荷数据采用每月预测值时的机组台数优化配置结果详见附录B表B3场景B1,经济成本见表1场景B1。设置不确定集的波动范围为预测值的±20%,改变不确定集取端点值个数的多少,得到机组配置台数详见附录B表B3场景B2和B3,得到系统成本见表1场景B2和B3。β为在12个典型日的计算周期内,不确定集取上界(下界)的个数,当其为0,表示不考虑不确定性。

表1 不同不确定性下经济成本比较Table 1 Comparison of optimal cost under various uncertainty

从表1可以看出,将只采用柴油发电机供电模式下各场景的经济成本与采用微电网供电模式下各场景的经济成本比较可知,只采用柴油组发电机发电,需配置5台柴油发电机,全年的总成本高于含风机和光伏发电的微电网总成本。说明虽然可再生能源初始投资成本较高,但由于运行费用较小,采用风机、光伏等可再生能源机组不仅具有环保性还具有经济性。

从机组台数的优化配置结果可以看出,随着系统的不确定性增加,微电网系统会减小可再生能源机组配置,增加柴油发电机组的配置。原因是随着系统的不确定性增加,弃电率增加,为保证弃电率不超过10%,减小可再生能源出力而增大柴油机的发电量,以提高系统的鲁棒性。从表1中的经济成本可以看出,当风、光和负荷的不确定性增大,无论是柴油发电机供电系统还是微电网系统,系统的运行费用都随之增大。

在不考虑不确定性的情况下,确定优化配置的机组台数后,以运行成本最小为目标函数优化各运行变量,给出在2月、6月、9月和12月4个月份典型日内的各机组出力曲线,如图2所示。图中，Pload为负荷功率，Pwt为风机的发电功率，Ppv为光伏发电功率。

从图2可以看出,在2月和12月,风力发电充足,会产生较多的弃电量,柴油发电机处于最小出力。而在6月和9月,全天负荷增大,风力发电的减小,光伏发电增大,在白天,光伏发电较好地弥补了风力发电的缺额,减小了柴油发电机的开启和储能的充放,说明风、光具有良好的互补性;在下午和傍晚,开启柴油发电弥补由于风机和光伏发电量减小引起的负荷缺额。

图2 不考虑不确定性时四季典型日各机组出力Fig.2 Output power of each unit in classic days of four seasons without considering uncertainty

在求解过程中发现,单位台数的风机经济性高于光伏发电的经济性。虽然光伏发电和风电的单位功率运行成本相同,求解算出的单位功率的边际增量(对偶变量)也相同,但由于风机全年功率的最大值为13.61 kW,最小值为2.01 kW,而光伏发电在早晨和晚间功率出力为0 kW,全年最大发电功率为11.18 kW,所以单位台数风机发电的总功率更大,边际增量更大,导致采用Benders分解方法配置的风机台数多于光伏的台数,经济性更好。

当系统的不确定性如场景B3所示时,确定机组台数后,以运行成本最小为目标函数,对各运行变量进行优化,给出在2月、6月、9月和12月4个月份的典型日内的各机组出力曲线,如图3所示。

图3 考虑不确定性时四季典型日各机组出力Fig.3 Output power of each unit in classic days of four seasons considering uncertainty

将图3各时刻的功率与图2各时刻功率进行比较,从图3可以看出,虽然减少了风机的配置台数,但在2月和12月,由于风、光及负荷不确定性的增加,负荷和风、光出力的波动更大,在09:00至17:00时仍有较多的弃电量。在6月和9月,对比柴油发电机09:00至14:00的发电量,发现柴油发电机发电量有所增加,发电功率的波动性也更大。

4.2 采用NSGA-Ⅱ的优化配置结果

采用NSGA-Ⅱ,取弃电量和系统总成本为目标函数,不确定集波动范围为20%,不确定集取边界值的个数同场景B3,取各机组台数为优化变量,种群个数为50,进化代数为20,迭代收敛后得到8组Pareto最优解,优化配置结果详见附录B表B4,经济成本见表2。

表2 NSGA-Ⅱ优化配置成本Table 2 Optimal configuration result of NSGA-Ⅱ

从机组台数的优化配置结果可以看出,柴油机、光伏、风机的台数相对固定,随着储能台数的增加,系统投资成本逐渐增加,运行成本逐渐降低,系统的总成本逐渐增加,弃电量逐渐减小。

比较分析配置N4和配置N5,当配置的储能和柴油发电机台数相同,可再生能源机组的总台数也相同,投资成本相同,但是配置N4的弃电量为35 943 kW·h,高于配置N5 的弃电量12 217 kW·h;配置N4的运行成本为15.16万元,低于配置N5的运行成本21.55万元。可知单位台数风机发电比光伏发电更加经济,但弃电量有所增加。原因是单位台数的风机发电量高于光伏的发电量。当配置的风机台数比例较高时,可再生能源的发电量更高,柴油发电机的运行时间更少,因此经济性更好,但是弃电率较高。从配置N1和配置N5对比也可发现,要达到相同的可再生能源功率渗透率,配置风机台数比例较高时,总可再生能源机组台数较少,投资成本也较小,更具经济性,与Benders分解方法的配置结果一致。

当系统具有相同的不确定性时,将NSGA-Ⅱ求解结果中最具经济性的方案配置N1与本文提出的二层鲁棒优化模型场景B3中的配置结果对比,可知两种配置储能台数相同,可再生能源和柴油发电机的总容量相同,都为390 kW,说明基于本文模型算法的配置结果具有合理性。通过对比发现在系统的不确定性较大时,采用Benders分解算法配置结果会减小可再生能源机组的配置,增大柴油发电机机组的配置以提高系统的鲁棒性。

从经济成本上来看,采用NSGA-Ⅱ配置的运行成本为16.23万元，小于Benders分解算法的运行成本30.91万元。从弃电量上来看,采用Benders分解方法的弃电量为51 739 kW·h，小于NSGA-Ⅱ的N1配置的弃电量53 452 kW·h。采用Benders分解方法的配置由于减少了可再生能源机组的台数,系统配置的弃电量有所下降。将配置N1机组台数带入Benders分解方法中的可行性检验子问题中,得到松弛变量的值为226.56,说明该方法不满足在二层鲁棒优化模型中不确定集作用下的所有约束条件。原因是本文构建了最小—最大模型的运行子问题,并采用Lagrange对偶的方法对问题进行了解耦,求解的结果为最大不确定性情况下的运行成本,而采用NSGA-Ⅱ求解的运行成本是在不确定集作用下的最小运行成本,所以采用本文提出的二层鲁棒优化模型的运行费用更大,柴油发电机组台数更多。因此,本文提出的模型能较好地体现系统的鲁棒性,能提高系统的抗风险能力,对运行子问题的建模也更符合实际。

仿真在CPU为2.30 GHz的IBM-PC,MATLAB 2012a的环境下运行,优化通过调用CPLEX和YALMIP优化工具箱完成。从求解时间上看,采用Benders分解求解模型经过11次迭代即可获得结果,所需时间为106 s,而NSGA-Ⅱ迭代需要求解1 000次优化才能获得结果,所需时间为444 min。采用Benders分解求解方法采用对偶变量返回外层决策变量的边际增量信息,充分体现了内层运行问题对外层投资问题的影响,提高了模型的求解效率。

5 结语

本文以独立型交流微电网的投资费用、运行费用、弃电费用和停电费用之和最小为目标函数,构建了包含风、光和负荷不确定集的二层鲁棒优化模型;采用最小—最大模型表征表示不确定性对内层运行子问题的影响,用Benders分解方法对模型内外层进行迭代求解,提高了模型的求解效率。在算例分析中,将基于Benders分解方法的配置结果与采用NSGA-Ⅱ的配置结果进行对比,采用本文提出的模型能根据风、光及负荷不确定性的大小提升微电网的鲁棒性,增强系统抵抗风险的能力,证明了模型的有效性和合理性。

由于风、光、负荷偏离预测值的不确定性随着时间的推移有可能发生变化,在本文研究的基础上,后续还需要计及该因素影响,研究更准确的机组容量配置方法。

本文的研究工作受到国网浙江省电力公司科技项目(5211DS15002A)资助，谨此致谢。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 丁明,王波,赵波,等.独立风光柴储微网系统容量优化配置[J].电网技术,2013,37(3):575-581.

DING Ming, WANG Bo, ZHAO Bo, et al. Configuration optimization of capacity of standalone PV-wind-diesel-battery hybrid microgrid[J]. Power System Technology, 2013, 37(3): 575-581.

[2] XU L, RUAN X B, MAO C X, et al. An improved optimal sizing method for wind-solar-battery hybrid power system[J]. IEEE Trans on Sustainable Energy, 2013, 4(3): 774-785.

[3] 江全元,石庆均,李兴鹏,等.风光储独立供电系统电源优化配置[J].电力自动化设备,2013,33(7):19-26.

JIANG Quanyuan, SHI Qinjun, LI Xinpeng, et al. Optimal configuration of standalone wind-solar-storage power supply system[J]. Electric Power Automation Equipment, 2013, 33(7): 19-26.

[4] 马溪原,吴耀文,方华亮,等.采用改进细菌觅食算法的风/光/储混合微电网电源优化配置[J].中国电机工程学报,2011,31(25):17-25.

MA Xiyuan, WU Yaowen, FANG Hualiang, et al. Optimal sizing of hybrid solar-wind distributed generation in an islanded microgrid using improved bacterial foraging algorithm[J]. Proceedings of the CSEE, 2011, 31(25): 17-25.

[5] RAMIREZ-DIAZ A, RAMOS-REAL F J, MARRERO G A. Complementarity of electric vehicles and pumped-hydro as energy storage in small isolated energy systems: case of La Palma, Canary Islands[J]. Journal of Modern Power Systems & Clean Energy, 2016, 4(4): 604-614.

[6] BIE Z H, XIE H P, HU G W, et al. Optimal scheduling of power systems considering demand response[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(2): 180-187.

[7] CHEN H C. Optimum capacity determination of stand-alone hybrid generation system considering cost and reliability[J]. Applied Energy, 2013, 103: 155-164.

[8] 余舟子,郭力,刘文建,等.独立微网随机优化规划软件及其实现[J].电力系统自动化,2015,39(6):18-23.DOI:10.7500/AEPS20140207002.

YU Zhouzi, GUO Li, LIU Wenjian, et al. A stochastic optimal planning software for stand-alone microgrid and its implementation[J]. Automation of Electric Power Systems, 2015, 39(6): 18-23. DOI: 10.7500/AEPS20140207002.

[9] 李丰,张粒子,舒隽.考虑间歇式电源与储能的随机柔性优化调度方法[J].电力系统自动化,2014,38(5):1-7.DOI:10.7500/AEPS20130717011.

LI Feng, ZHANG Lizi, SHU Jun. A flexible stochastic optimal scheduling approach considering intermittent power and energy storage[J]. Automation of Electric Power Systems, 2014, 38(5): 1-7. DOI: 10.7500/AEPS20130717011.

[10] 李斯,周任军,童小娇,等.基于盒式集合鲁棒优化的风电并网最大装机容量[J].电网技术,2011,35(12):208-213.

LI Si, ZHOU Renjun, TONG Xiaojiao, et al. Robust optimization with box set for maximum installed capacity of wind farm connected to grid[J]. Power System Technology, 2011, 35(12): 208-213.

[11] 谢鹏,彭春华,于蓉.大规模间歇式电源接入电网多目标鲁棒优化调度[J].电网技术,2014,38(6):1479-1484.

XIE Peng, PENG Chunhua, YU Rong. Multi-objective robust optimized scheduling of power grid connected with large-scale intermittent power sources[J]. Power System Technology, 2014, 38(6): 1479-1484.

[12] 向月,刘俊勇,魏震波,等.考虑可再生能源出力不确定性的微电网能量优化鲁棒模型[J].中国电机工程学报,2014,34(19):3063-3072.

XIANG Yue, LIU Junyong, WEI Zhenbo, et al. Robust model of microgrid energy optimization with uncertain renewable energy sources[J]. Proceedings of the CSEE, 2014, 34(19): 3063-3072.

[13] 茆美琴,孙树娟,苏建徽.包含电动汽车的风/光/储微电网经济性分析[J].电力系统自动化,2011,35(14):30-35.

MAO meiqing, SUN shujuan, SU jianhui. Economic analysis of a microgrid with wind/photovoltaic/storages and electric vehicles[J]. Automation of Electric Power Systems, 2011, 35(14): 30-35.

[14] 赵波.微电网优化配置关键技术及应用[M].北京:科学出版社,2015.

[15] 王成山,洪博文,郭力.不同场景下的光蓄微电网调度策略[J].电网技术,2013,37(7):1775-1782.

WANG Chengshan, HONG Bowen, GUO Li. Dispatch strategies of PV-battery microgrid in different scenarios[J]. Power System Technology, 2013, 37(7): 1775-1782.

[16] 郭力,富晓鹏,李霞林,等.独立交流微网中电池储能与柴油发电机的协调控制[J].中国电机工程学报,2012,32(25):70-78.

GUO Li, FU Xiaopeng, LI Xialing, et al. Coordinated control of battery storage and diesel generators in isolated AC microgrid systems[J]. Proceedings of the CSEE, 2012, 32(25): 70-78.

[17] 梅生伟,郭文涛,王莹莹,等.一类电力系统鲁棒优化问题的博弈模型及应用实例[J].中国电机工程学报,2013,33(19):47-56.

MEI Shengwei, GUO Wentao, WANG Yingying, et al. A game model for robust optimization of power systems and its application[J]. Proceedings of the CSEE, 2013, 33(19): 47-56.

[18] BRNDERS J F. Partitioning procedures for solving mixed-variables programing problems[J]. Numerische Mathmatik, 1962, 4(1): 238-252.

[19] GUPT A, AHMED S, CHEON M S, et al. Solving mixed integer bilinear problems using MILP formulations[J]. Siam Journal on Optimization, 2013, 23(2): 721-744.

CapacityConfigurationModelforRobustOptimizationofStand-aloneMicrogridBasedonBendersDecomposition

LIUSiyi1,ZHAOBo2,WANGXiangjin2,QIUHaifeng2,LINXiangning1

(1. State Key Laboratory of Advanced Electromagnetic Engineering and Technology (Huazhong University of Science and Technology), Wuhan 430074, China; 2. Electric Power Research Institute of State Grid Zhejiang Electric Power Company, Hangzhou 310014, China)

To improve the robustness of power source configuration for stand-alone microgrid, a double layer configuration model for robust power source capacity is built considering the intermittency and volatility of wind, solar radiation and load. The outer layer is the master problem regarding power source capacity optimization, the inner layer is the subproblem regarding operational optimization including uncertainty sets of wind, solar radiation and load. The dual problem is established to decouple the subproblem and the bilinear terms in the subproblem are converted to linear terms using the big M method, iterate the master problem and subproblem alternatively until the optimal solution is obtained. The proposed method is compared with improved non-dominant sorting genetic algorithm (NSGA-Ⅱ) in the test case. The testing result shows the robust performance and solving efficiency of the proposed model is higher than usual. The rationality and effectiveness of the model is verified.

This work is supported by National High Technology Research and Development Program of China (863 Program) (No. 2015AA050104).

microgrid; optimal configuration; robust optimization; Benders decomposition; uncertainty sets

2016-12-28;

2017-04-11。

上网日期: 2017-06-27。

国家高技术研究发展计划(863计划)资助项目(2015AA050104)。

刘思夷(1993—),女,硕士研究生,主要研究方向:分布式发电及微电网优化配置。E-mail： liusiyi@163.com

赵 波(1977—),男,通信作者,博士,教授级高级工程师,主要研究方向:分布式能源及微电网关键技术。E-mail: zhaobozju@163.com

汪湘晋(1992—),男,硕士研究生,主要研究方向:微电网优化配置及储能模型。E-mail: hfwangxj@126.com

(编辑万志超)