基于完全信息动态博弈理论的光储接入网源协调规划
金秋龙, 刘文霞, 成 锐, 刘宗歧
(新能源电力系统国家重点实验室(华北电力大学), 北京市 102206)
基于完全信息动态博弈理论的光储接入网源协调规划
金秋龙, 刘文霞, 成 锐, 刘宗歧
(新能源电力系统国家重点实验室(华北电力大学), 北京市 102206)
为解决中国西北地区大量弃光问题,探讨合理的网源规划策略,文中引入绿色证书交易机制,基于完全信息动态博弈理论,以光伏、储能和电网作为博弈参与者,分析市场环境下三方的博弈关系,建立光储网协调规划模型,并结合西北电网调度运行策略,通过具体算例验证模型实用性。结果表明,在市场环境下,光伏、储能、电网三方进行动态博弈规划,既有利于提高电网消纳光伏的积极性,又有利于避免光伏无序扩张,可为目前光伏电站规划中的场网不协调问题提供改进方案。
绿色证书交易; 完全信息动态博弈; 博弈树; 逆向归纳法; 网源协调规划
0 引言
近年来,在国家政策激励下,西北地区光伏企业发展迅猛,但弃光现象突出。储能系统并网和网架扩展规划被认为是解决当前光伏消纳难题的有力举措。但由于目前光伏、储能与电网几个利益主体的独立规划,在造成投资浪费的同时,弃光难题也没有得到很好地解决。因此,在当前市场环境下,如何实现光储网协调规划成为值得研究的重点问题。
针对新能源接入后的网源协调规划问题,国内外学者已经取得了初步的研究成果。文献[1]针对风电随机性特点,以系统调峰需求为限制修改电源规划方案后进行电网规划,但其本质上仍为顺序进行的源网规划。文献[2-3]针对风电场并网特性,采用场景聚类技术,建立以规划水平年总成本最小为目标的网源协调输电网扩展规划模型。文献[4]在考虑投资和运行费用外,还以最小化负荷损失为目标,研究含风电场的多目标电网规划问题。文献[5-6]在以最小化总投资费用为目标的基础上,进一步引入风险控制策略,研究风电机组接入后的输电网规划问题。
但上述论文并没有考虑市场机制,在规划过程中,未考虑新能源消纳难题与各主体间合理的运行策略,造成并网规划容量较大且投资浪费的问题。文献[7]为探讨风电并网的市场出路,解决当前电网消纳风电积极性不高的问题,引入碳交易过程,将风电的节能减排效益量化为实际的经济价值,提升风电—电网联盟收益。上述问题在光伏并网规划中同样存在。
在市场环境下,也有不少学者引入博弈论研究新能源并网规划问题。文献[7]基于合作博弈理论,分析风电规划运行中风电场和电网的合作运行策略,建立风电—电网联盟收益最大的风电并网容量模型。文献[8]建立风光储混合电力系统的博弈规划模型,提出了5种合作/非合作博弈规划模式,探讨风光储容量优化配置方案。文献[9]运用双人零和博弈理论,将电网和大自然当作两个博弈参与者,研究风电接入电力系统后的静态备用容量规划问题。文献[10]基于非合作博弈理论,建立电力市场环境下风电场和火电机组的长期随机规划古诺模型,研究风火容量优化配置方案。上述研究可分为从合作博弈和非合作博弈两个角度出发,而二者的本质区别在于博弈决策过程中,参与者能否达成具有约束力的协议,若能达成则为合作博弈,反之即是非合作博弈。
针对中国西北地区光储并网规划问题,由于大量市场资本涌入,打破了原本电网企业—发电集团两方博弈局面,形成多方投资者哄抢资源、相互竞争的博弈格局。由于各方参与者均独立追求个体利益最大化,且相互之间缺乏共谋的有效性,难以制定有效协议,无法形成合作联盟。因此,本文采用非合作博弈理论研究光储网协调规划问题。
综上,本文针对西北区域发电厂并网运行方式[11],引入可再生能源配额制与绿色证书交易机制[12]量化光伏环境效益,基于非合作博弈中的完全信息动态博弈理论,以光伏、储能和电网作为三方博弈参与者,建立光储网协调规划模型,探讨了不同主体投资方案下的均衡结果与绿色证书交易价格变化下各方投资者的效益变动。
1 可再生能源配额制运行机制
欧美等发达国家为解决新能源发电、上网和市场消纳等难题,提出了可再生能源配额制机制,配额实施的责任主体为电网企业,由政府强制执行。
绿色证书交易是可再生能源配额制的组成部分,一份绿色证书代表相应单位的可再生能源发电量,电网企业的可再生能源义务最终表现为必须持有的绿色证书数目。电网企业可以采用两种方式来完成相应的义务:一是通过双边合同从可再生能源获得电能;二是从其他已经完成了规定配额的电力企业购买其超额完成“义务量”而获得的绿色证书。设某电网绿色证书配额为N,实际证书持有量为M,则该电网通过可再生能源交易市场可获收益为:
WG,TGC=λTGC(M-N)
(1)
式中:WG,TGC为绿色证书交易收益;λTGC为绿色证书单位电量的交易价格。
本文以1 kW·h可再生电量作为单位证书面值,以一年为期限作为绿色证书结算周期。需要特别说明的是,若M 本文在规划年负荷预测的基础上,考虑西北电网运行方式,进行光储接入后的网源协调规划。图1所示为典型的光储并网系统运行示意图。 图1 光储并网系统运行示意图Fig.1 Schematic diagram of grid system operation with photovoltaic station and storage battery 由图1可见,光伏电站、储能系统和电网公司互联互动,收益相关。光伏企业:决策并网容量,影响电网绿色证书交易收益与储能调峰、备用收益;电网公司:决策网架,追求最小化投资,无法保证光伏消纳;储能系统:决策并网容量,影响光伏上网电量与电网售电、证书交易收益。三者决策变量互相影响,形成博弈关系。 博弈论是利用严谨的数学模型,研究多个决策主体之间存在利益关联甚至冲突时,各决策主体如何根据自身能力及所掌握的信息,做出有利于自己或决策者群体的数学理论。形成一个博弈格局的基本元素为参与者、策略、收益与均衡。 1)博弈参与者。光伏电站、储能系统和电网公司作为参与者构成三方博弈,以下用P,B,G表示三方参与者。 2)参与者策略。P,B,G进行博弈时,光伏电站和储能系统的策略为各自的容量,分别记为PP和PB,电网公司策略为网架扩展规划,记为LG。 3)参与者收益。P,B,G收益为其收入与成本之差,分别记为FP,FB,FG,具体收益模型见下文。 博弈模式下,各投资主体的效益涉及整个寿命周期的全过程,本文考虑资金贴现率,采用年平均收入和成本计算各参与者的收益,具体收益模型如下。 3.1.1光伏电站收益模型 光伏电站的收益包括年售电收入WP,SEL,政府新能源补贴WP,SUB,光伏电池报废收入WP,SCR;成本包括光伏电站初期建设成本CP,INV,运行维护成本CP,WOM和运行考核成本CP,ASS。西北电网对并网光伏电站的功率波动与预测有严格的考核标准[11],具体如下:①规定光伏电站月均10 min和1 min最大功率变化分别不超过装机容量的33%和10%,每超出1%按10分/月考核,每分对应1 000元惩罚金额;②规定光伏电站短期和超短期功率预测月平均绝对误差分别小于15%和10%,每超出1%按装机容量×0.2分/MW考核,每分对应1 000元惩罚金额。 光伏收益函数如下式: (2) 式中:WP,SCR=PPDP,其中PP为光伏电站装机容量,DP为单位功率光伏报废收入;CP,INV=PPUP,其中UP为单位功率光伏造价;CP,WOM=PPMP,其中MP为单位功率光伏年维护费用;τ为银行利率;TP为光伏电站寿命;τ/[1-(1+τ)-TP]为设备等值年系数。 3.1.2储能系统收益模型 储能系统的收益包括年辅助服务收入WB,AUX,成本包括从电网购电成本CB,PUR,初期建设成本CB,INV和运行维护成本CB,WOM。储能系统在电网运行中用于调峰、备用等辅助服务,其辅助服务收入计算如下[13]: (3) 式中:cPE为单位调峰收入;cRE为单位备用收入;EB,RE,t为t时段储能参与系统备用容量,EB,RE,t=EB,t-EB,PE,t,其中EB,t为t时段储能电量,EB,PE,t为t时段储能参与调峰电量。 储能系统收益函数如下式: FB=WB,AUX-CB,PUR- (4) 3.1.3电网公司收益模型 电网的收入来自于售电收入WG,SEL和绿色证书交易收入WG,TGC;成本包括电网从光伏电站年购电成本CG,PUR,以及电网为接纳光伏进行的网架扩建成本CG,TR。收益函数如下式: FG=WG,SEL+WG,TGC- (5) 为了简化计算,本文忽略了光伏接入引起的系统网损变化。 光伏、储能和电网进行网源规划博弈时,光伏作为电源侧,首先制定其策略PP,之后电网和储能根据系统运行情况,依次制定各自策略LG和PB,最后P,B,G三方以最大化各自收益为目标,优化调整博弈策略至最优,由此可知这是一个动态博弈过程。为简明起见,假设博弈阶段的所有信息均公开,博弈参与者互相掌握对方的全部策略信息,且博弈参与者具有完全理性。 基于此,本文建立光储网协调规划动态博弈模型求解三方均衡策略,优化目标如下: (6) 本文考虑经济调度策略,以常规火电机组消耗能源成本CGEN与储能运行成本CBESS最小为目标,对各博弈方案进行仿真计算。具体数学模型为: (7) 式中:PGi,t为火电机组i在t时段的输出功率;NG为火电机组台数,NB为储能系统数量;uGi,t和uGi,t-1分别为火电机组i在t时段和t时段前的启停状态变量,0表示火电机组处于停机状态,1表示火电机组处于开机状态;αi,βi,γi为机组运行耗量特性参数;ηi为机组启动耗量特性参数。储能运行成本CBESS即为其辅助服务收入WB,AUX,此处是从调度角度出发考虑。 系统仿真运行过程中的约束条件如下。 1)可调度光伏出力约束 PPOi,t≤PPOi,ava,t (8) 式中:PPOi,t为t时段光伏出力;PPOi,ava,t为t时段光伏最大出力,即本文允许因为线路容量约束与调峰、备用约束引起的弃光。 2)火电机组技术约束 ①输出功率上下限约束: uGi,tPGi,min≤PGi,t≤uGi,tPGi,max (9) 式中:PGi,max和PGi,min分别为火电机组i的输出功率上、下限。 ②爬坡率约束: PGi,dw≤uGi,tPGi,t-uGi,t-1PGi,t-1≤PGi,up (10) 式中:PGi,up和PGi,dw分别为火电机组i的向上爬坡速率和向下爬坡速率。 ③最小启停时间约束: (11) 3)储能系统技术约束 ①充放电功率约束: (12) ②存储电量约束: EBi,min≤EBi,t≤EBi,max (13) 式中:EBi,t为储能i在t时段的存储电量;EBi,max和EBi,min分别为储能存储电量上、下限。 4)系统约束 ①功率平衡约束: (14) 式中:Pload,t为时段t的有功负荷;NP为光伏电站数量。 ②旋转备用约束: (15) (16) 式中:RP,up,t和RP,dw,t分别为t时段系统应对光伏功率波动设置的正负旋转备用;Rload,up,t和Rload,dw,t分别为t时段系统应对负荷波动设置的正负旋转备用。 ③线路容量约束: (17) 由上述博弈模型可知,由于博弈参与者均独立追求自己的利益最大化,博弈问题很难通过统一的优化模型进行求解。现有的博弈均衡求解方法包括逆向归纳法[14]、剔除劣势策略[14]、序列线性化[15]、分散迭代[16]等。对于上述完全信息动态博弈模型,本文应用逆向归纳法求解纳什均衡。 对于完全信息动态博弈模型,通常采用扩展式表述描述参与者战略的动态选择。本文应用图论中树的概念,直观描述博弈中参与者的行动顺序、策略信息、博弈收益。 图2中初始结和终点结表示博弈的开始和结束,决策结是博弈进行到某个时点上参与者的决策点,终点结也是决策结。需要特别说明的是,任何一个完全信息动态博弈的决策结都可以作为初始结并与其全部后续结构成一个子博弈。 图2 光储网协调规划博弈树Fig.2 Game tree for coordination planning of photovoltaic station, storage battery and grid 定理2[17]:任何完全信息动态有限博弈都存在子博弈精炼纳什均衡。 由上述定理可知,若使得光伏、储能、电网三方博弈参与者策略集为有限集合,即可将本文模型转化为完全信息动态有限博弈,则可采用逆向归纳法求解子博弈精炼纳什均衡,求解步骤如下,模型求解流程详见附录A。 步骤1:输入原始数据和参数。初始化建立博弈模型所需的数据,包括负荷信息、光伏出力数据、电价、设备造价等计算参与者收益必需的参数。 步骤2:生成博弈参与者策略集合。光储容量从零开始分别以一定步长增加至容量上限,生成光储策略集合;在每个光伏策略下,通过遗传算法,剔除明显不合理的电网规划方案,生成相应电网策略集合。 步骤3:按光伏、电网、储能排序分层,生成博弈树。 步骤4:考虑规划年负荷预测数据与光伏出力数据,模拟调度运行,计算每条分支线的参与者收益。 步骤5:博弈树简化。由最下层开始,各子博弈模型独立寻找纳什均衡,并将这些子博弈的初始结看作原博弈的终点结,并在新的终点结上标注纳什均衡收益,在简化后的博弈树上重复上述步骤,逆向推进至原博弈树初始结。 步骤6:判断系统是否找到子博弈精炼纳什均衡。若找到均衡,进入步骤7,否则返回步骤2。 步骤7:输出模型均衡解(相比较于均衡,均衡解特指始于原博弈树的初始结且止于终点结的唯一一条连贯的均衡路径)。 本文选取的典型系统、负荷数据、光伏出力数据、电价信息、设备参数、火电机组参数等详见附录A。仿真时间跨度为一年,等值年系数取为0.08。绿色证书交易价格设为0.2元/(kW·h),设定仿真系统可再生能源发电量要求占系统总能源需求的10%。参考美国加州地区统计数据[18],本文设定光伏短期和超短期功率预测越限概率为10%,月平均绝对误差分别设为20%和15%。光储容量上限设为系统最大负荷。 5.2.1博弈均衡结果 本文考虑不同主体参与下的博弈规划情况,表1为光储网规划、光网规划和光储规划三种方案下的纳什均衡结果。 表1 三种规划方案下的纳什均衡结果Table 1 Nash equilibrium under three plans 由表1可知,3种规划方案的差异主要体现在规划容量、网架扩展线路和总收益的不同。对比均衡结果下的光伏电站并网容量可知,方案1和方案2接纳光伏的能力明显高于方案3,而且,在方案1下,博弈参与者能获得最大收益,方案2收益次之,方案3收益最低。从方案2和方案3的对比还可看出,网架扩展对于系统接纳光伏能力的提升作用和博弈参与者的收益增益优于储能系统并网规划。 5.2.2光储网三方收益变化曲线 图3所示为博弈参与三方收益曲线,表示随着光伏装机容量的逐步增加,电网和储能取相应的均衡策略下,三方的收益变化情况。 由图3可见,光伏收益出现了连续的增大、减小情况,这是因为当光伏装机容量较小时,系统有充裕的光伏消纳空间。当装机容量提高到25 MW,电网和储能从自身利益出发,选择策略为不进行规划,光伏消纳受限,收益下降。随着光伏装机容量持续升高,电网和储能进行容量和网架扩展规划,光伏上网电量增加,三方收益提高。当光伏装机容量进一步提高时,系统消纳光伏能力已达极限,光伏收益下降。从图3还可看出,在可再生能源配额制模式下,电网收益受光伏装机容量影响很大,当装机容量较小时,电网需要支付巨额费用购买绿色证书。 图3 光伏、储能、电网三方收益Fig.3 Benefits of photovoltaic station, storage batteries and grid 5.2.3绿色证书交易价格影响分析 引入绿色证书交易机制后,不同的绿色证书交易价格将影响博弈参与者的收益与均衡策略。表2与图4为不同证书价格下,光伏、储能、电网三方的纳什均衡结果与收益变化情况。 表2 不同绿色证书交易价格下的纳什均衡结果Table 2 Nash equilibrium under different green certificate trading prices 图4 绿色证书价格变化下的收益曲线Fig.4 Benefits curves under different green certificate trading prices 由表2与博弈三方收益变化曲线可知,绿色证书交易价格从0.1元/(kW·h)提高到0.2元/(kW·h)后,光伏最优并网容量从44 MW提升到了49 MW,博弈三方收益也均有提高。但当证书价格进一步增加时,三方博弈规划策略不再变化,光伏与储能收益不再增加。这说明在光伏电站发展前期,较高的绿色证书交易价格能够提高电网消纳光伏的积极性,使得储能与电网企业在利益驱使下增加投资,促进光伏并网,但当光伏容量增加到一定规模后,电网负荷水平决定了系统接纳光伏上限,此时,即使继续提高绿色证书交易价格,博弈参与者也不会改变均衡策略。 本文在可再生能源配额制市场下,引入绿色证书交易机制,基于完全信息动态博弈理论,建立考虑光储接入的网源协调规划模型,并分析证书价格变动下博弈参与者的均衡策略与收益变化。结果表明,在当前的电力市场环境下,光伏、储能、电网三方进行动态博弈规划,能在保证参与者利益最大化的同时,实现光储合理布局与电网统筹协调规划,对解决国内目前新能源并网的协调规划问题具有一定的理论价值。 但是,本文在博弈阶段假定参与者信息安全公开且参与者具有完全理性,未考虑信息不对称下的各方博弈,同时没有对光伏出力波动和电网安全风险等不确定因素作深入探讨,后续研究可从上述两个方面进行改进。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。 [1] 高赐威,吴天婴,何叶,等.考虑风电接入的电源电网协调规划[J].电力系统自动化,2012,36(22):30-35. GAO Ciwei, WU Tianying, HE Ye, et al. Generation and transmission coordinated planning considering wind power integration[J]. Automation of Electric Power Systems, 2012, 36(22): 30-35. [2] 洪绍云,程浩忠,曾平良,等.基于相关场景聚类的发输电联合扩展规划[J].电力系统自动化,2016,40(22):71-76.DOI:10.7500/AEPS20151129005. HONG Shaoyun, CHENG Haozhong, ZENG Pingliang, et al. Coordinated generation and transmission expansion planning with clusters of correlative scenarios[J]. Automation of Electric Power Systems, 2016, 40(22): 71-76. DOI: 10.7500/AEPS20151129005. [3] 刘文霞,李鹤,赵天阳,等.风电多点并网的网源协调输电网扩展规划[J].现代电力,2015,32(1):38-45. LIU Wenxia, LI He, ZHAO Tianyang, et al. Coordination of generation and transmission expansion planning for wind power integration at multi-points[J]. Modern Electric Power, 2015, 32(1): 38-45. [4] 王茜,张粒子.采用NSGA-Ⅱ混合智能算法的风电场多目标电网规划[J].中国电机工程学报,2011,31(19):17-24. WANG Qian, ZHANG Lizi. Multi-objective transmission planning associated with wind farms applying NSGA-Ⅱ hybrid intelligent algorithm[J]. Proceedings of the CSEE, 2011, 31(19): 17-24. [5] 郑静,文福拴,李力,等.计及风险控制策略的含风电机组的输电系统规划[J].电力系统自动化,2011,35(22):71-76. ZHENG Jing, WEN Fushuan, LI Li, et al. Transmission system planning with risk-control strategies for power systems with wind generators[J]. Automation of Electric Power Systems, 2011, 35(22): 71-76. [6] 黄裕春,杨甲甲,文福拴,等.计及接纳间歇性电源能力的输电系统规划方法[J].电力系统自动化,2013,37(4):28-34. HUANG Yuchun, YANG Jiajia, WEN Fushuan, et al. Transmission system planning considering capability of accommodating intermittent generation sources[J]. Automation of Electric Power Systems, 2013, 37(4): 28-34. [7] 刘文霞,凌云頔,赵天阳.低碳经济下基于合作博弈的风电容量规划方法[J].电力系统自动化,2015,39(19):68-74.DOI:10.7500/AEPS20141014002. LIU Wenxia, LING Yundi, ZHAO Tianyang. Cooperative game based capacity planning model for wind power in low-carbon economy[J]. Automation of Electric Power Systems, 2015, 39(19): 68-74. DOI: 10.7500/AEPS20141014002. [8] 梅生伟,王莹莹,刘锋.风-光-储混合电力系统的博弈论规划模型与分析[J].电力系统自动化,2011,35(20):13-19. MEI Shengwei, WANG Yingying, LIU Feng. A game theory based planning model and analysis for hybrid power system with wind generators-photovoltaic panels-storage batteries[J]. Automation of Electric Power Systems, 2011, 35(20): 13-19. [9] MEI S, ZHANG D, WANG Y, et al. Robust optimization of static reserve planning with large-scale integration of wind power: a game theoretic approach[J]. IEEE Trans on Sustainable Energy, 2014, 5(2): 535-545. [10] MASOUMZADEH A, NEKOUEI E, ALPCAN T. Long-term stochastic planning in electricity markets under carbon cap constraint: a Bayesian game approach[C]// IEEE PES Innovative Smart Grid Technologies-Asia (ISGT-Asia), November 28-December 1, 2016, Melbourne, Australia: 466-471. [11] 国家电监会印发华东、东北、南方、华中、西北区域发电厂辅助服务管理及并网运行管理实施细则[J].电站信息,2009(1):13-16. [12] 任东明.中国可再生能源配额制和实施对策探讨[J].电力系统自动化,2011,35(22):25-28. REN Dongming. China’s renewable portfolio standards and implementing countermeasures[J]. Automation of Electric Power Systems, 2011, 35(22): 25-28. [13] 赵书强,王扬,徐岩,等.基于机会约束目标规划的高风电接入比例下大规模储能与火电协调调度[J].中国电机工程学报,2016,36(4):969-977. ZHAO Shuqiang, WANG Yang, XU Yan, et al. Coordinated dispatch of large scale energy storage system and thermal generation in high wind power penetration level system based on chance constrained goal programming[J]. Proceedings of the CSEE, 2016, 36(4): 969-977. [14] MAVRONICOLAS M, PAPADOPOULOU V, SPIRAKIS P. Algorithmic game theory and applications[M]. Hoboken, NJ, USA: John Wiley & Sons Inc, 2007: 571-591. [15] ZHU Q, ZHANG J, SAUER P W, et al. A game-theoretic framework for control of distributed renewable-based energy resources in smart grids[C]// American Control Conference (ACC), June 27-29, 2012, Montreal, QC, Canada. [16] MA Z, CALLAWAY D S, HISKENS I A. Decentralized charging control of large populations of plug-in electric vehicles[J]. IEEE Trans on Control Systems Technology, 2013, 21(1): 67-78. [17] FUDENBERG D, TIROLE J. Game theory[M]. Cambridge, MA, USA: MIT Press, 1992. [18] GLASSLEY W, KLEISSL J, SHIU H, et al. Current state of the art in solar forecasting: appendix A California renewable energy forecasting, resource data and mapping[R]. California Institute for Energy and Environment, 2010. CoordinatedPlanningModelforPhotovoltaicStation,StorageBatteryandGridBasedonCompleteInformationDynamicGame JINQiulong,LIUWenxia,CHENGRui,LIUZongqi (State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources (North China Electric Power University), Beijing 102206, China) To solve the tremendous abandonment of photovoltaic light in Northwest China and seek a reasonable generation and transmission planning strategy, the tradable green certificate policy is introduced. A planning model for photovoltaic station, storage battery and grid based on complete information dynamic game is proposed and verified by specific example under the operation strategy. Example analysis shows that, in the market environment, the dynamic game based planning model is beneficial not only to increasing grid initiative in accommodating photovoltaics but also avoiding disorderly expansion of the photovoltaic station. And also providing solutions for the current mismatch issue of planning between the photovoltaic station and grid. tradable green certificates; complete information dynamic game; game tree; backward induction method; generation and transmission coordinated planning 2017-01-13; 2017-05-03。 上网日期: 2017-07-21。 金秋龙(1993—),男,通信作者,硕士研究生,主要研究方向:电力系统规划。E-mail: jinqiulong93@163.com 刘文霞(1967—),女,博士,教授,主要研究方向:电力系统规划与可靠性、电力系统风险评估。E-mail: liuwenxia001@163.com 成 锐(1994—),男,硕士研究生,主要研究方向:电力系统可靠性。 (编辑章黎)2 光储网协调规划博弈关系分析

3 博弈模式下光储网协调规划模型
3.1 各主体投资效益模型






3.2 光储网协调规划博弈模型与调度运行策略



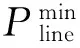
4 基于逆向归纳法的博弈模型求解


5 算例分析
5.1 典型系统及参数
5.2 结果分析




6 结语

