基于福州市降水量数据研究降水期权定价

黄 峰，王保乾

(河海大学商学院，江苏 南京 211100)

基于福州市降水量数据研究降水期权定价

黄 峰，王保乾

(河海大学商学院，江苏 南京 211100)

为应对干旱、洪涝等降水事件给相关经济主体带来的风险，基于1953年1月至2016年12月福州市月均累积降水量数据，运用威尔克斯法对降水量进行建模，利用蒙特卡罗模法对降水期权进行定价从而得到降水期权价值，并提出发展我国降水期权的政策建议。

降水期权；定价；威尔克斯法；蒙特卡罗模拟

福建省地处我国东南沿海，以山地丘陵地形为主，且水系密布，河流众多，河网密度大，季风环流因受到全球气候变化的影响，加剧了干旱、洪涝灾害对福建省各地的破坏力，极易引发各种地质灾害和水生灾害[1]。

面对气候变化下降水量变动引发的干旱、洪涝灾害造成的人身与财产损失，运用单一的保险工具进行风险管理无法满足现实的需求。降水期权作为一种典型的天气衍生产品，相比于保险，其风险管理所适用的领域更广。只要风险管理的标的与降水相关或挂钩，降水期权就能够发挥作用。通过降水期权，农民、涉农企业、用水生产企业、水力发电企业、保险公司等就能够有效管理自身面临的降水不确定性风险。同时，降水期权的出现也丰富了金融投资的品种，在一定程度上起到活跃金融市场、提升金融市场效率、完善金融市场结构机制的作用。

本文借助威尔克斯法，基于1953年1月至2016年12月福州市月均累积降水量数据，从福州市月降水量频率和数量两方面构建降水模型，并采用蒙特卡罗模拟法[2]计算降水期权价值，为降水期权的实践提供实证经验和政策建议。

1 降水模型的建立

以降水期权为代表的降水衍生品，不同于权益衍生品。降水衍生品的收益中没有市场给予补偿的系统风险。因此，降水衍生品的定价主要根据历史数据得到期望值，并在风险中性世界中运用无风险利率对期望值进行贴现而完成定价[3]。对降水期权定价的首要工作就是基于历史数据建模估计期望值[4-6]。

降水量的建模不同于温度、风力等天气变量，降水量的观测值包含更多的不确定性。对于降水期权定价而言，运用统计方法建立降水量模型较适合，本文采用威尔克斯法。威尔克斯法主要有两个步骤：①使用马尔科夫链建立降水频率模型，②采用适当的分布拟合数据建立似然条件下的降水数量模型[4,7]。

1.1 降水频率模型的建立[8-9]

马尔科夫链是一个离散随机过程，用于描述一个状态序列。序列中某一时刻的随机变量状态值取决于在该时刻之前有限个随机变量的状态值。变量状态值的所有可能取值构成的集合，称为随机变量的状态空间。随机变量从某一时刻某一状态值变为下一时刻某一状态值这一事件发生的概率，称为马尔科夫链的转换概率。

定义随机变量Xt为一个二值变量，取值0或1，得到随机变量的状态空间Ω={0,1}。因本文采用月度数据，降水量在月度同比或月度环比下仅有增加或减少两种可能性，故假定只存在降水增加或降水减少两种状态。定义：

(1)

pij=Pr{Xt+1=j|Xt=i}

(2)

式中：pij表示从t时刻的状态i到t+1时刻的状态j的转换概率；Pr{Xt=j|Xt-1=i}表示已知t时刻随机变量的状态为i的条件下，t+1时刻随机变量的状态为j的概率。假设某一时刻随机变量的状态值取决于在该时刻之前m个随机变量的状态值，则称m为马尔科夫链的阶数。因此，m阶马尔科夫链的转换概率为

Pr{Xt+1|Xt,Xt-1,…,X1}=

Pr{Xt+1|Xt,Xt-1,…Xt+1-m}

(3)

转换概率的计算，需要基于样本数据进行极大似然估计，根据：

(4)

式中：i,…,jk表示从状态i经过m次变化到状态k的状态变化路径；ni,…,jk表示数据中满足按照状态i经过m次变化到状态k的状态变化路径的数据个数；ni,…,j·表示数据中状态i经过m次变化到状态k的状态变化路径下，所有k可取状态值的数据个数的累加和。在二值状态空间下，有：

(5)

马尔科夫链的建立是降水频率模型建立的关键。而在马尔科夫链的建立过程中，最关键的是马尔科夫链阶数的选择。马尔科夫链阶数的选择主要依靠赤池的AIC赤池信息准则和施瓦茨的BIC贝叶斯信息准则。通过选择AIC、BIC中最小数值所对应的阶数来确定马尔科夫链的阶数。假设状态空间有s个状态，这些状态的取值是离散的自然数，s个状态对应于自然数0，1，…，s-1。则s个状态的马尔科夫链似然函数：

(6)

假设n表示数据的个数，则s个状态对应的m阶马尔科夫链的AIC、BIC函数分别是：

AIC(s,m)=-2Ls+2sm(s-1)

(7)

BIC(s,m)=-2Ls+2smln(n)

(8)

基于上述理论，使用福州市1953年1月到2016年12月的月均累积降水量数据进行研究，数据来源于中国气象数据网和福州市气象局网站。福州市属于季风性气候，降水量的变化具有明显的季节性。如果数据按照时间顺序研究，就必须考虑季节性效应问题。为避免该问题，将数据按月分组，对每个月分别建立马尔科夫链。如此一来，每个月的转换概率能够分别通过不同的似然函数和AIC、BIC准则确定，同时消除了季节性影响，提高了转换概率估计的精度[10]。

根据表1可知，无论是AIC准则还是BIC准则，当选择马尔科夫链的阶数为1阶时，所有月份的AIC、BIC的函数值是最小的。因此应采用两状态、1阶马尔科夫链对福州市每个月的降水量进行频率建模。确定马尔科夫链的阶数后，开始计算马尔科夫链下的转换概率。

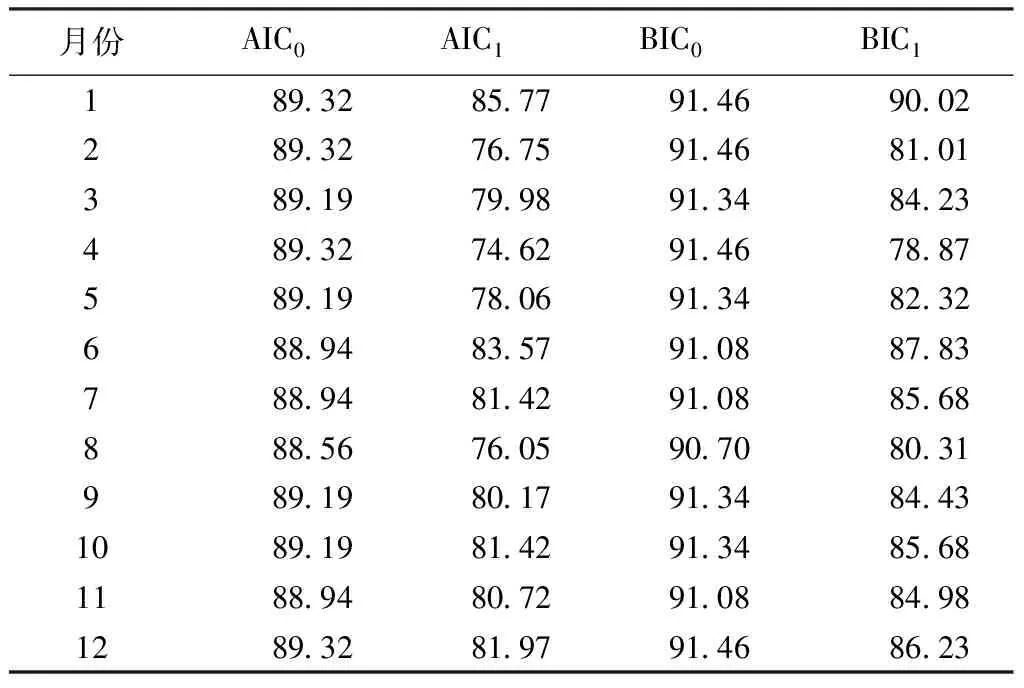
表1 每月不同阶AIC、BIC准则的函数值

由表2可知，同一月份年与年之间降水状态出现改变的概率要比降水状态不出现改变的概率高，即降水量的变动是降水增加和降水减少交替出现的概率较高，而连续两年出现降水增加或降水减少的概率较低。通过建立降水频率模型，能够大致了解在年份时间上每个月降水量变动的转换过程，以统计角度为下一年同期月份的降水增加或减少事件发生的预测提供依据，为降水期权的定价提供间接参考。

表2 每月降水变动的转换概率值

1.2 降水数量模型的建立

降水数量模型的建立主要依据历史数据选择合适的分布进行拟合。通过绘制每月降水量的频数分布直方图(图1)，可以观测数据比较接近于哪一种分布。由图1可见，降水量分布主要呈现两种形态：图1(a)的“左高密右低疏”的非正态分布以及图1(b)的近似正态分布。因此，需要对数据进行正态性检验。正态性检验主要采用JB(Jarque-Bera)统计量进行。

图1 福州市降水量频数分布直方图

在5%的置信概率下，从表3可知，仅4—6月的数据接受了正态分布的假设，而其余月份均拒绝假设。仅用一个统计分布对月降水量数据进行拟合，必然会存在偏差。所以，对不同月份应采用不同的分布进行拟合。根据正态分布性检验，对4—6月的数据采用正态分布进行拟合。对其他月份的数据分别采用伽马分布、指数分布和瑞利分布进行拟合，并对这3种分布拟合出的结果同原始数据进行比较，选取一个最佳的分布。表4为4个统计分布的汇总。表5和表6为除4—6月的其他月份降水量数据拟合结果比较。

表3 降水量正态性检验结果

根据数据拟合的结果，多数分布拟合出的期望值与实际值非常相近，但不同分布下拟合的标准差、偏度和峰度具有较大的差异。综合比较表5和表6中3种分布下的标准差、偏度和峰度可以得出，相较于其他分布，伽马分布对降水量拟合更贴近实际值。故对除4—6月的其他月份降水量采用伽马分布进行拟合。至此，确定了福州市每月的月均累计降水量分布。通过建立降水数量模型，可以得到福州市每月降水量的期望值，为降水期权的定价提供了直接的参考依据。

表4 分布的概率密度函数及其数字特征

表5 降水量伽马分布拟合结果比较

2 降水期权的定价

a.基于历史数据建模估计期望值。期权主要分为香草期权和奇异期权。香草期权主要包括看涨期权和看跌期权两类，而奇异期权主要包括障碍期权、亚式期权等。由于降水是不可交易资产，降水期权只能通过现金交割，所以需要通过设定交易乘数使降水期权可交易化。

表6 降水量指数分布和瑞利分布拟合结果比较

用Cmonth和Pmonth分别表示每月降水的看涨期权和看跌期权的价值，有：

Cmonth=e-r(T-t)max(Xmonth-K,0)κ

(9)

Pmonth=e-r(T-t)max(K-Xmonth,0)κ

(10)

式中：κ为交易乘数，元/mm；Xmonth为每月降水的期望值，最小变动单位为0.1 mm，month表示对应的月份；K为执行降水量，单位和最小变动单位与降水期望值相同；r为无风险利率；(T-t)表示期权的剩余到期时间，a。

不同月份的降水量有不同的特点，为了避免极端降水过少或过多两种情况的发生给期权卖方带来巨大损失，期权卖方可以选择出售障碍期权。理论上，障碍期权取决于标的价格或指数在一段时间内是否达到某个特定的水平。障碍期权可以分为敲出期权和敲入期权，当标的资产价格或指数达到一定水平时，敲出期权失效，敲入期权生效。因为降水不同于权益证券，所以本文的障碍期权是一种“类障碍期权”：当降水达到一定水平时，敲入、敲出期权的回报保持一个固定值。假设障碍值为Hmonth，用Fmonth表示回报的固定值，敲入、敲出期权的回报分别用Imonth和Omonth表示，有：

(11)

(12)

b.在风险中性世界中运用无风险利率对期望值进行贴现。蒙特卡罗模拟以“试验”方法进行，通过构造描述相应的概率过程，从已知的概率分布中进行抽样，从数学模拟中得到随机变量的期望值作为问题的近似解。设蒙特卡罗模拟的次数为N，每次蒙特卡罗模拟得到的降水量期望值为Xi，可以得到看涨期权和看跌期权在蒙特卡罗模拟下的期权价值[11-12]：

(13)

(14)

假定κ=10元/mm，期权剩余到期日为1 a，无风险利率为1.5%，蒙特卡罗模拟次数为10万次，进行香草期权的定价，期权价值的最小变动单位为1元。表7为在福州1月月均累积降水量数据下，不同执行降水量的降水看涨期权和降水看跌期权的价值。由表7可以看出，降水看涨、看跌期权价值与执行降水量之间的关系与权益类看涨、看跌期权有着相同的规律。执行降水量越高，对看涨期权而言价值越低，对看跌期权而言价值越高。

表7 福州1月降水看涨期权与看跌期权的期权价值

运用相同方法，也可以为敲入期权和敲出期权进行定价。其他参数不变，敲入期权的障碍值为 10 mm，敲出期权的障碍值根据每个月降水的特点来设定。以福州1月降水量为例，设1月的障碍值为200 mm。表8为在福州1月月均累积降水量数据下，不同执行降水量的降水敲入期权和降水敲出期权的价值。

降水敲入期权的价值与行权降水量之间的关系同看跌期权，降水敲出期权的价值与行权降水量之间的关系同看涨期权。正因为障碍期权中障碍值的存在限制了可能存在的无限收益，因此障碍期权比普通期权便宜。通过比较表7、表8的结果，同一执行降水量条件下，降水敲出期权的价值低于降水看涨期权，降水敲入期权的价值低于降水看跌期权。

表8 福州1月降水敲入期权与敲出期权的期权价值

3 降水期权发展的政策与建议

a.积极学习国外先进经验成果，夯实国内发展降水期权的基础。包括降水期权在内的天气衍生品在国内是较为新鲜的事物，且当前国内并没有可供交易的天气衍生品。美国早在20世纪90年代就已推出温度变量为代表的天气衍生品，并相继上市风力、降水等以天气变量为标的的天气衍生品。芝加哥商品交易所向美国的主要城市提供降雨期货、降雨期货期权、降雪期货、降雪期货期权等种类的降水衍生品。降水衍生品为美国涉水经济主体、政府等利益相关者提供了有效的风险管理工具。中国发展降水期权，应当深入了解美国在天气衍生品方面定价和应用的有关理论基础和实际操作，同时比较中美在发展天气衍生品市场基础条件方面的异同点，为发展我国天气衍生品交易奠定基础。

b.加快推进交易所商品期权的发展。当前我国的大连商品交易所、郑州商品交易所虽然已经分别上市豆粕期权和白糖期权，但仍处于起步阶段，而绝大多数其他品种的商品期权则集中于场外交易。场外期权的交易存在门槛高、合约价格高、市场流动性差等问题，导致场外商品期权的交易非常不活跃。降水等天气方面因素对大多数商品，特别是农产品有着明显的影响。正因为农产品与天气变量之间的高度相关性，若没有积极活跃的商品衍生品市场，就没有相应的天气衍生品市场的生存空间。一个交易活跃、流动性强的商品衍生品市场，才能为天气衍生品市场提供良好的发展沃土；而积极的天气衍生品市场也会促进商品衍生品市场的健康发展，从而提升整个金融市场的运行效率，使金融更好地为实体经济服务。

c.强化金融机构之间的交流合作。2016年中央一号文件中提出，完善农业保险制度，探索开展重要农产品目标价格保险，以及收入保险、天气指数保险试点，稳步扩大“保险+期货”试点[13]。相较于期货公司，保险公司更为广大涉水利益相关者所熟悉。期货公司直接同涉水利益相关者进行接触，往往存在较大的沟通障碍。保险公司向涉水利益相关者提供以保险为工具的风险管理手段时，自身也承担了相应的风险，也同样需要相应的风险管理工具进行风险管理。对今后可能出现的降水指数保险，期货公司可以提供降水衍生品，从而将保险公司和期货公司两个本质上同为风险管理的金融机构联系在一起，在保险公司和期货公司之间产生良性互动，以合作带动我国降水期权的发展。

d.加强涉水利益相关者的普及宣传引导，提高使用衍生品进行风险管理的积极性和主动性。推出降水期权后，只有参与者积极参与，市场才能活跃存在。加大对涉农企业、用水生产企业、水力发电企业等涉水利益相关者衍生品金融知识的宣传普及，引导涉水利益相关者从被动地看天吃饭观念转变为主动使用降水期权等衍生品进行风险管理，消除天气因素影响可能带来的潜在损失，才能从市场需求基础上保证降水期权在内的天气衍生品的正常发展。

[1] 程学宁，卢毅敏.基于SOM和PCA的闽江流域地表水水质综合评价[J].水资源保护，2017，33(3)：59-67.

[2] 王晶晶，樊尊荣.含水层非均质性对地下水蒙特卡罗模拟结果的影响[J].水资源保护，2017，33(1)：46-51.

[3] WOLFGANG K H，BRENDA L C.The implied market price of weather risk[J].Applied Mathematical Finance，2012，19(1):59-95.

[4] ALEXANDRIDIS A K.Weather derivatives：modeling and pricing weather-related risk[M].West-Berlin：Springer-Verlag，2013：241-243.

[5] 彭龙，孙小丽.天气衍生品中的制冷指数看涨期权定价研究与实证[J].北京邮电大学学报(社会科学版)，2013，15(1):87-90.

[6] CABRERA B L，ODENING M，RITTER M.Pricing rainfall futures at the CME[J].Journal of Banking & Finance，2013，37(11): 4286-4298.

[7] 王晶.天气衍生品定价模型的构建[J].统计与决策，2016(15)：152-155.

[8] HESS M.Modeling and pricing precipitation derivatives under weather forecasts[J].International Journal of Theoretical & Applied Finance，2016，19(7):1650051.

[9] GIOVANNI M.Rainfall derivatives pricing with an underlying semi-Markov model for precipitation occurrences[J].Stochastic Environmental Research and Risk Assessment(SERRA)，2014，28(3):717-727

[10] LEOBACHER G，NGARE P.On modelling and pricing rainfall derivatives with seasonality[J].Applied Mathematical Finance，2011，18(1):71-91.

[11] 李诗云，朱晓武.雾霾指数期权合约设计及蒙特卡罗模拟定价[J].系统工程理论与实践，2016，36(10):2477-2488.

[12] 李永，夏敏，梁力铭.基于O-U模型的天气衍生品定价研究：以气温期权为例[J].预测，2012，31(2):18-22.

[13] 中共中央国务院.关于落实发展新理念加快农业现代化实现全面小康目标的若干意见[EB/OL].(2015-12-31)[2006-01-27].http：//news.xinhuanet.com/2016-01/27/c_1117916568.htm.

教育部重点支持领域科研专项(20116B31914)

黄峰(1992—)，男，硕士研究生，主要从事金融工程、金融计量、公司金融等研究。E-mail：fzbee1992@hhu.edu.cn

10.3880/j.issn.1003-9511.2017.06.009

F830

A

1003-9511(2017)06-0044-06

2017-05-12 编辑：胡新宇)