期刊论文下载次数的概率密度服从对数正态分布

毛国敏，吴何珍，生冬梅

（1.中国地震局地球物理研究所，北京100081；2.中国地震局工程力学研究所，黑龙江 哈尔滨150080）

0 引言

对数正态分布函数是一种常见的用来描述正偏态数据的分布，在实际问题中有着非常重要的应用.韩春明［1］对新疆西准噶尔地区古生代地层铜的微量数据进行统计，认为该地区古生代地层铜含量服从于对数正态分布；胡晓华等［2］对上海股票交易所584个交易日大盘日成交量进行统计分析，认为股市大盘日成交量服从或近似服从对数正态分布；于洋［3］介绍了对数正态分布在股票价格模型中的应用.

期刊论文下载次数是一个非常客观的指标，显示论文被使用和受重视的程度，论文下载的次数越多说明该论文受到同行的关注也越高.随着期刊检索系统的发展，获取期刊论文被下载的数据已成为可能.本文利用期刊论文下载次数的数据，运用对数正态模型，研究期刊论文下载次数指标的分布问题.

1 资料来源及数据样本的基本情况

本文的主要观测对象是 《CT理论与应用研究》期刊 （简称A刊）论文下载次数的分布.A刊在中国学术期刊影响因子年报［4］中的学科类别为自动化技术计算机技术 （TP）类或军事医学与特种医学 （R8）类，2013年起科学类别更改为综合性科学技术 （N／Q，T／X）类或综合性医药卫生 （R）类，学术影响力一般，载文规模较小.为了进一步验证期刊论文下载次数的分布规律，我们再用另两种不同学科类别、载文规模和学术影响力的B刊和C刊论文下载次数资料，分析其分布规律.其中：B刊为某地球物理 （P）类精品期刊，学术影响力较大，载文规模中等；C刊是为某高校学报，学术影响力较大，载文规模较大.

A刊自创刊 （1992年）至2011年发表的不含信息、报道等有效论文1 063篇，其中有4条论文下载次数为0，与文献［5］样本数相比，本文删除了4条下载为0的记录.表1（见 101页）为3种期刊论文下载次数数据基本统计量，3种期刊的样本数据分别为1 059、2 156和14 017.

从表1中的偏度和峰度系数的绝对值远大于0可知，3种期刊的论文下载次数的分布呈现左偏、尖峰态，远偏离正态分布.从图1（见 102页）中原数据0点的分布状态也可直观地看出左偏尖峰的分布特点.原始数据来源于文献［6、7］，对数据感兴趣的读者可向作者索取.表2为从原始数据经统计得到的A刊论文下载次数x及其概率y，B刊和C刊论文下载次数x及其概率y见表3.

表1 3种期刊论文下载次数数据基本统计情况

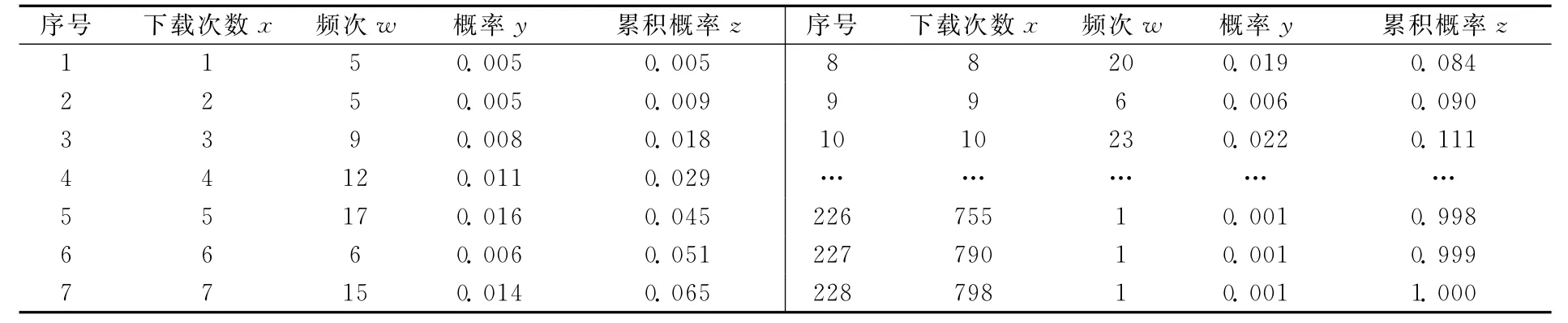
表2 A刊论文下载次数及其概率

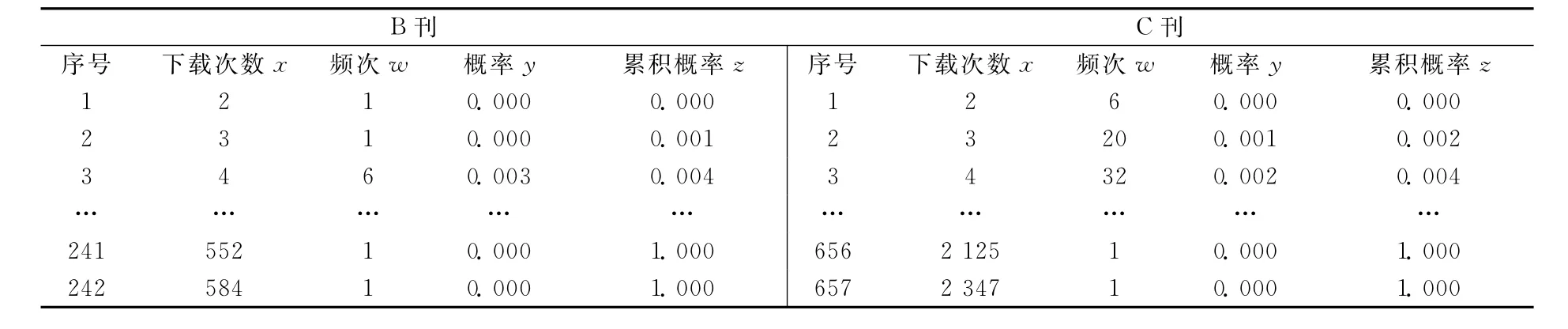
表3 B刊和C刊论文下载次数及其概率

2 原理和假设

2.1 原理

在概率论与数理统计学中，对数正态分布是对数为正态分布的任意随机变量的概率分布.如果X是正态分布的随机变量，则变量为对数正态分布；同样，如果变量Y＝exp（X）是对数正态分布，则为正态分布［8～10］.

对于x＞0，对数正态分布的概率分布函数为：

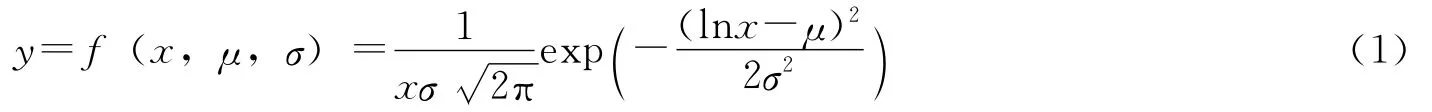
式中μ≥0，σ＞0.

理论上，μ和σ分别为变量对数的平均值与标准差，相应的分布函数为

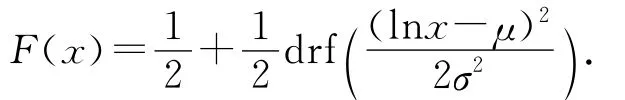
2.2 假设

根据分布函数和密度函数的定义［11、12］，显然，表2中的论文下载次数的概率y即为下载次数x的密度函数，累积概率z即为x的分布函数.根据y随x的增加先快速上升、达最高点后又迅速下降、逐步趋近于0的特点（见 图1原数据0点），我们不妨假设y与x的关系如公式（1），即假设论文下载次数的概率密度服从对数正态分布.

3 分析方法

我们运用SPSS20软件工具中非线性迭代计算方法，用公式（1）模型对数据进行拟合，并与理论对数正态分布进行比较.为叙述方便和清晰起见，先以A刊为例，利用对数正态函数为模型，对A刊论文下载次数的概率密度分布进行分析，得到模拟结果.为了检验模型的可靠性，用B刊和C刊再做进一步的验证.

3.1 模型拟合

表4为3种期刊论文下载次数分布的对数正态模型检验，从表4中A刊栏检验统计量可知，A刊模型通过统计检验，F＝994.255，且拟合优度优良，R2＝0.898，说明对数正态模型对A刊的论文下载次数的密度分布拟合是可行的，模型拟合可以解释原数据89.8%的变异.

表5为3种期刊论文下载次数分布的对数正态模型参数估计及其检验，从表5中A刊栏检验统计量可知，A刊的模型参数μ和σ的均通过检验，估计值分别为3.783、1.115，与理论值3.690、1.078非常接近.

表4 三种期刊论文下载次数分布的对数正态模型检验

表5 三种期刊论文下载次数分布的对数正态模型参数估计及其检验

图1（a）为A刊下载次数的原数据、对数正态模型拟合及理论对数正态概率分布图，图中：点○为下载分布的原数据，点＊为对数正态模型拟合，点□为对数正态函数分布理论值.从图1（a）点＊曲线可见，对数正态模型与原数据拟合良好，并且与理论函数基本重合.

通过上述分析，我们可以得出A刊论文的下载次数指标服从对数正态分布.

3.2 模型验证

为了进一步验证论文下载次数服从对数分布这个结论的可靠性，我们再利用B刊和C刊的数据，类似A刊的分析过程，经统计检验，B刊和C刊也通过模型的检验（见 表4中的B刊和C刊栏），论文下载指标密度分布与对数正态函数拟合，且拟合优度优良，决定系数R2分别为0.959和0.972；由于B刊和C刊样本比A刊大，与A刊相比拟合更优.模型参数μ和σ的也通过检验（见 表5中的B刊和C刊栏），B刊的估计值分别为3.769和0.933，与理论值3.732、0.879非常接近，C刊为4.473和0.962，与理论值4.365、0.937也非常接近.对比图1（b）和图1（c）中点○和点□曲线，点○和点□基本重合，可直观地看出B刊和C刊论文的下载次数是服从理论对数正态分布的.

4 讨论与结论

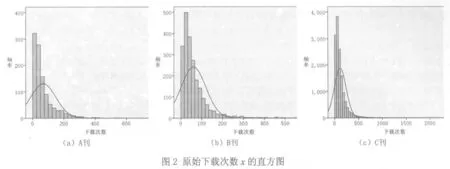
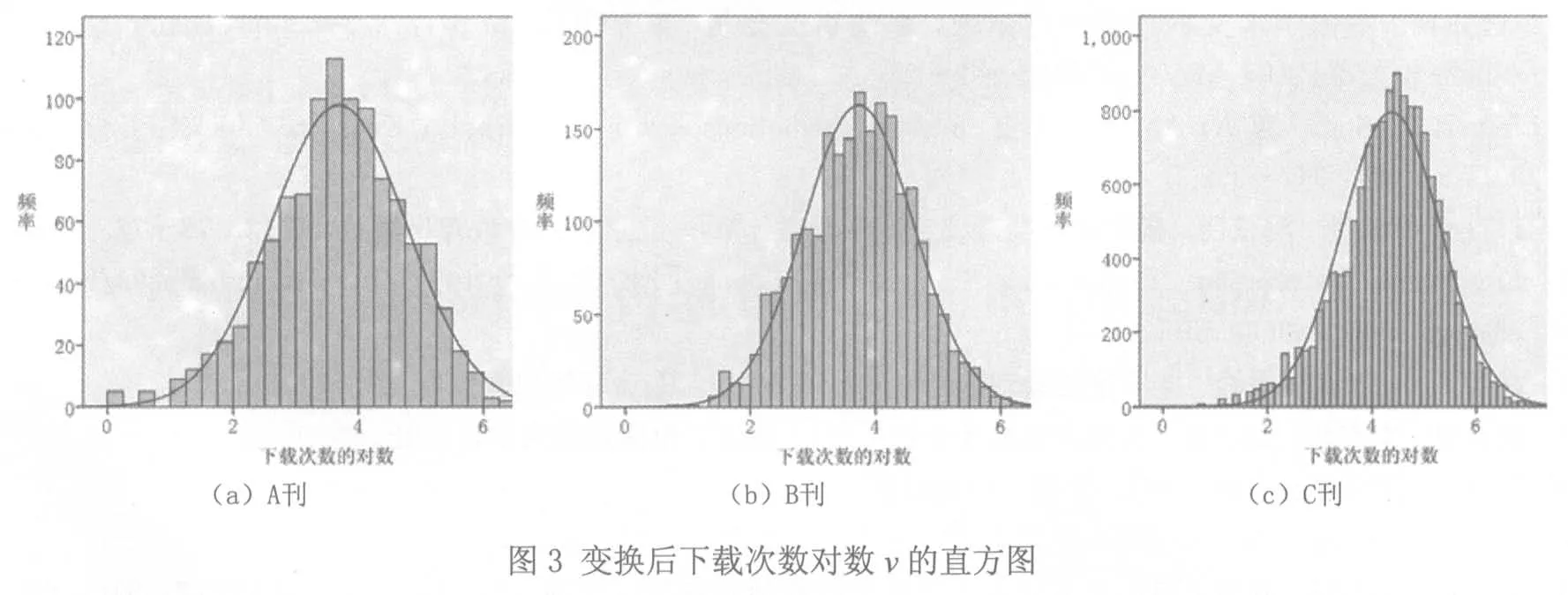
图2为3种期刊论文下载次数直方图，从图中明显可看出期刊论文下载次数指标是非正态的，呈左偏、尖峰态.通过分析，我们知道了期刊论文下载次数指标概率密度是服从对数正态分布的.那么，根据对数正态分布的性质，对x取对数，即令v＝ln（x），则v变量服从正态分布.图3为3种期刊v的直方图，从图3看出，v的分布与正态分布几乎是吻合的.

在撰写本文过程中我们本着大胆假设、小心求证的态度，做了大量的探索性工作.为了充分验证，我们从A、B和C刊随机抽取50%的数据进行模拟，也证明论文下载次数指标的概率密度服从对数正态分布.实际上，C刊是某高校学报，包括：社会科学版 （1993～2002年）、农业科学版（1994－）、哲学社会科学版 （2002－）、医学版 （2006－），在文献［6、7］中统称为C刊，我们分别对C刊各分学科版样本单独进行拟合，还将A刊和B刊两个样本相加组成的新样本进行拟合，都通过模型检验且拟合优度良好，得出类似如图1的分布结果，对应的直方图也与图2和图3相似.通过这些探索性的分析工作，说明期刊论文下载次数指标概率密度服从对数正态分布具有 “加法性”，这种简单的分布特征可能揭示了论文下载次数隐含的某种普通规律性.

在运用数理原理对观察对象做统计分析时，一般对数据的分布有一定要求，很多数理模型如方差分析和回归分析要求数据服从正态分布［13、14］.在我们以往观察和研究期刊计量指标关系时［5、15、16］，发现其他指标的偏度系数和峰度系数的绝对值远大于0，即指标变量的密度分布远离标准正态函数.实际上，许多社科类指标的概率密度分布都不是正态的，这就为有效合理利用这些指标做深入进一步分析带来了困难.当指标数据分布为非中心对称时，一般不能直接利用原始数据做分析，需要对原始数据的分布有所了解，在此基础上做必要的变换，才能做有关的统计分析.

理论上，随机变量的密度分布函数，包含了该变量的全部信息.获得变量的密度函数，就等于掌握了变量的内在规律，只有对变量的分布有所了解，才能合理、有效地利用数据进行各种分析.因此，期刊指标的分布规律研究是一项基础性工作.

本文通过对不同学科类别、载文规模和学术影响力、有一定代表性的3种期刊进行分析，得出期刊论文下载次数指标x的概率密度服从对数正态分布，因此，一般不能直接用x与其他指标如被引次数等做回归等统计分析，必须对x做适当的变换.在理论上，如果对x取对数变换，v＝ln（x），这样v就能满足正态分布的要求，可以利用v做各种对数据有要求的分析，为今后进一步合理利用论文下载次数这一指标提供了参考依据.通过本文探索性的分析和研究，论文下载次数这种简单的对数正态分布规律有可能具有普适性，实际情况是否如此，有待进一步验证.