小学数学课堂中学生“元认知”存在的问题及改进策略

◎李崇

小学数学课堂中学生“元认知”存在的问题及改进策略

◎李崇

在日常数学教学中，教师对学生学习水平的评估和学生对自身学习水平的评估往往在准确性上有所偏差。一方面，教师对于学生学习水平的评估往往是基于自身的教学经验展开，有经验的教师往往会从学生的日常作业、试卷中评估学生的学习，进而采取有效的教学措施来弥补或强化，以此帮助学生查漏补缺，从而完成数学认知结构的创建，因此评估比较接近于学生的真实水平。另一方面，作为学生个体，其自身对学习水平的评估除自身作业、试卷的完成情况作为参考外，更大一部分源自教师对其的社会性评价和学科性评价，这种评价在学生那里是不够准确的，因此和他们谈学习时，他们对自己的评价往往感觉很“好”，似乎并不清楚自己哪些部分已经掌握，哪些部分并没有掌握。

笔者认为，后面这种现象和学生的“元认知”发展水平有密切联系。“元认知”(Metacognition)的概念是美国心理学家弗拉威尔（J.Flavell）于1976年在《认知发展》一书中首先提出的。“元认知”是关于认知的认知，是个体对自己的认知加工过程的自我觉察、自我反省、自我评价与自我调节，它包括元认知知识、元认知体验和元认知监控三个成分，它们相互联系、密不可分。学生在数学学习过程中，对自身的认知加工的自我觉察、自我反省、自我评价与自我调节往往处于较低水平，与其真实的水平存在较大偏差，很多时候他们的学习处在一种“无意识”的状态——在学，而不知道真正学到了什么水平；一直在学，但不知道为什么学；遇到困难也不知道如何去解决，通常会选择逃避困难。

一、自我认识缺失，新旧知识无法融通

学生对于新知的学习，往往是在原有旧知基础上拓展延伸。如果学生对于新知没有深度建构，当天的作业只是“套用”当天的公式，那么就会当天作业正确率很高的假象。但是随着新知的不断累加，学生缺乏新旧知识沟通融合的能力，不能把知识“由厚变薄”，那么在运用时不能灵活运用，缺乏融会贯通的能力，甚至在解决问题时出现公式“张冠李戴”而导致错误。

（一）问题缘起

苏教版《义务教育教科书·数学》六年级下册第二单元“圆柱和圆锥”基础概念比较多，知识间的横向和纵向联系都比较复杂，囊括的基本概念包括：侧面积、底面积、表面积、体积、横截面等，对圆柱和圆锥、圆柱和其它立方体的联系也在考察之列，笔者在教学此章节时自然不敢大意，对每节课的重点都做了强调和强化。单元结束后对本单元进行了例行检测，批改出来以后却发现，结果令人沮丧，学生大面积出错，很多题目只是单纯进行公式套用，结果学生居然不会。情急之下，我听写了常用的公式，收上来的答题纸验证了之前的猜测和担忧，学生对公式掌握得一塌糊涂。

（二）教学反思

公式遗忘是数学学习中的一种常见现象，很多教师都经历过，然而原因却往往是多方面的。比如，理解并记住圆柱的表面积公式V=S侧+2S底=πd+2πr2作为圆柱表面积这一课时的学习目标，在初学时学生的印象特别深刻，但是每当后续知识出现相似内容时，对于这一公式的冲击都十分巨大，原本单一的知识变得多样，原本孤立的知识被其它知识干扰。造成这一问题的关键在于学生在学习过程中往往缺乏有效的自我认知，无法灵活地根据自身的特点调整学习重心。只是在不停地接纳新知，造成知识容量越来越大，旧知和新知完全是独立的，新知无法同化旧知，旧知无法顺应新知，没有理解知识之间的联系，无法形成结构化和系统化。表现为学生无意识地被动学习，或者选择后学的知识，或者选择印象深刻的知识。这种认知活动往往在不经意间完成，学生自己也未必能说清楚，轮番冲击以后，学生往往出现学了后边忘前边，最后留存在脑海的东西越来越少。这也可以看作是学生个体对自身的学习存在调控水平低和自我意识弱的表现。

（三）改进策略

让学生对自己的学习过程进行有效认知是可以帮助知识常驻脑海中的。如何帮助学生进行有效自我认知呢？一般来讲，在学习新知以后，立刻对旧知和新知做出辨析往往收效甚好。如果新知能够同化旧知，抑或旧知顺应新知都可以建立更高一级的认知结构，而新知和旧知都成为其下位知识。比如圆柱的表面积公式学习结束后，可将圆柱的表面积公式和长方体的表面积公式进行同化学习，纳入到表面积这一上位概念中来。具体就是将圆柱的侧面积和长方体的侧面积进行类比，学生就可以发现，其实圆柱的曲面侧面积是长方体前后左右四个面“合四为一”，那么，长方体的侧面积也等于底面周长（长方形）×高，圆柱的底面积等同于长方体的底面积，采用的公式不同源于其形状不同。所以，学生在听写圆柱的表面积时，即使出现遗忘，也可以根据圆柱表面积线索追溯到长方体的表面积线索。如果能做到这一步，说明学生正在学会学习。这一过程反映了学生当遇到学习困难时可以自我觉察，厘清问题的症结，在原有的知识储备中寻找到有效的解决手段。

二、自我监控缺乏，练习缺省整体感知

问题解决往往是以情境方式呈现，随着年级的升高往往出现文字表述相对较长或者情境图相对丰富的状况。学生面对这样的问题解决时，读题往往囫囵吐枣，在没有深度理解题目的基础上盲目解答；或者由于心理认识特点的原因，在观察图文并茂的情境图时，注意力过于集中在图形情境，忽视了题目中的文字表述，缺乏必要的自我监控能力——不能整体感知题意，导致错误。

（一）问题缘起

解决实际问题是小学数学的一种常见题型。这种题目往往以文字或情境图为主要内容，在解题过程中需要学生对文字条件进行综合分析，完成数学的模型化建构。然而，日常教学中学生在该类题型上的水平差异却让很多一线教师头痛不已，笔者以苏教版《义务教育教科书·数学》六年级上册百分数单元习题为例。

乘坐飞机的每位旅客，携带行李超过20千克的部分，每千克要按飞机票原价的1.5%购买行李票。张芳从南京乘飞机到北京，票价打七折后是707元，南京到北京飞机票的原价是多少元？张芳带了30千克的行李，应付行李费多少元？

上边这道题发生的情境是飞机购票，其中涉及到的概念比较多，比如行李票、打折机票、机票原价等，对于行李票这一概念的理解则体现出了学生存在知识经验明显不足的问题。我梳理以后发现，对行李票的理解至少要包含以下两层意思：

第一，旅客自带行李不是一定要购买行李票，只是在超出20kg的部分才购买行李票。举个例子：乘客自带了30kg的行李，其中20kg属于免费，10kg则属于购票范围。

第二，行李票的购买是以原价机票为基准，和打折没有关系。上题中，行李费用应该是以求出来的原价为基础，与707元没有关系。

本道题条件众多，学生是否能真正理解呢？亦或是真正理解究竟需要多少时间呢？我要求学生花费3分钟左右时间将题目背下来，然后进行听写。听写的主要内容还是基于以上两点，结果成绩非常不理想，很多学生几乎无法对上述内容作出准确回忆，因此对数量关系无法进行整合判断，导致本题解题普遍存在困难。

（二）教学反思

“元认知”的一个主要功能是自我监控。那么学生在解决实际问题时的条件识别是如何进行的呢？笔者在和学生的谈话中得知，学生在题目的文本解读时注意力是平均分配的，通常是一口气读下来，几乎在读题中没有任何停顿，对于问题中的关键概念往往也是一掠而过，一般不会停下来想一下其真正含义。由于问题中的关键概念无法得到理解，以至于对题目整体数量关系的感知也就处于困顿状态。那么，这种问题的根源在什么地方呢？我认为，这和学生缺乏自我监控有关，对自己学习过程的监控往往是无意识的，对注意力的分配也是随机的，因此自我监控经常处于一种不可控状态。

（三）改进策略

帮助学生学会自我监控其实就是帮助学生在学习过程中建立起监控意识，学会对问题中的关键概念和关键关系分配更多的注意力。通俗一点来说，就是在问题中对问题要素做出主次判断和难易辨别，对主要方面予以特别关注，对关键概念予以重点理解。以上题为例，可以对问题的中心概念——行李票做出分析，以上图为例。

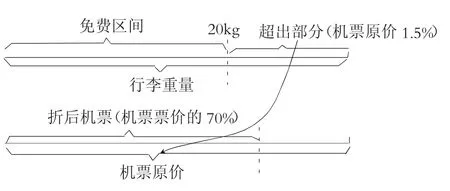
其中以图示法将行李超出部分和机票原价直接建立联系，可以有效解决行李票的单位“1”问题，这样对于30kg的行李如何购票就有了更好的认识。

关键概念的理解除了上题中采用的图示法以外，还可以通过打比方、类比等手段进行。比如在解决“体积相等的圆柱和圆锥，当底面积或高相等时，求另外一个量”时，经常会出现混淆的情况，学生之间就会用“高瘦子”和“矮胖子”来形象化地描述圆柱和圆锥，数量之间的倍数关系也就一目了然；再比如“周长相等的平面图形哪种面积大”时，有学生做出如下解释：周长相等可以看作若干个同学手拉手在一起，什么时候面积最大呢？当然是所有同学都把身子往后撤，这样形成的图形是圆，为什么长方形面积要比圆小呢？因为长方形里只有四位同学（顶点）把身子往后撤，等等。

曾经有人提出：教学生学习，不如教学生学会学习。这里边就蕴含着对“元认知”的深刻理解。超越解决实际问题这一微观层面，从更宏观层面看学习——这一过程本身就是非常复杂的，对学习活动本真的分析其实就是帮助学生学会更多学习的策略和方法，渗透并掌握一些“元认知”策略，帮助学生对自身的教学活动进行有效积极监控、自觉调节，从时间和精力上对学生的学习进行优化和整合，必能帮助学生从一个被动的学习者转化为一个积极的学习者。

课题项目：本文系江苏省“十三五”规划立项课题“构建小学数学‘情理相融’课堂的实践研究”阶段性研究成果，课题编号：D/2016/02/06。

（作者单位：江苏省徐州市贾汪区塔山镇葛湖小学）

（责任编辑：杨强）