在计算教学中寻找“理”与“法”的平衡点

◎纪玉洁

在计算教学中寻找“理”与“法”的平衡点

◎纪玉洁

计算教学是小学数学教学的重点内容，对学生的发展有着不可估量的作用。但是，计算教学也是教学的难点，有的教师认为，我不管怎么教，孩子就是不会算，就是一算就错。那么，如何做好计算教学呢？这个问题在我们教师中也有不同的声音。一部分教师认为，计算教学要“重视计算方法、算理理解不理解不重要”；另一部分教师则认为，计算教学“算理理解过繁、算法掌握过软、技能形成过难”，那我们在教学中究竟应该如何处理算理与算法的关系呢？

什么是算理？顾名思义，就是计算的道理，它是进行计算的理论依据，解释了计算中每个步骤的合理性，解决了“为什么这样算”的问题。

什么是算法？就是计算的方法，主要指计算的法则，通过简化，加入了人为的规定，形成了公式化、程序化的步骤，解决了“怎样算”的问题。

在教学中，我感到，算理和算法同样重要，两者相辅相成，缺一不可。领悟算理是理解算法的基础，而算法是对算理的提炼。理解算理让学生明白计算之“道”，掌握算法让学生找到计算之“路”，在教学过程中要使两者并重。同时，算理与算法的教学没有先后之分。就像我们准备做某一件事，并不需要把做这件事的道理弄得透彻明白，有时需要先根据已经积累的经验甚至直觉去做，在做的过程中再去思考清楚这样做的道理是什么，也就是“先知其然，再知其所以然”。“理通则法明”，“理”是“法”的基础；而“法熟则理悟”，“法”是“理”的概括。课堂上先教哪一个，一方面可以归为每位教师独特的教学艺术范围，另一方面也要根据教学内容进行适当调整。所谓教无定法，但贵在得法。

所以，在计算教学中，算理理解与算法掌握不可偏重，只有寻找到算理与算法的平衡点，才能使“理”“法”有效融合，浑然一体。

一、观察情境，孕伏基础性算法

小学生的思维以形象思维为主，所以，在计算教学中也要十分注重观察情境图，从中发现有助于新知学习的信息，为算理的理解和算法的建构提供帮助。

如在教学“9加几”时，苏教版教材上的情景图主体部分是盒子被分为10格，里面共有9个桃，一格空着，盒子的外面放着4个桃。问题是：一共有多少个桃？学生根据情境图可以很快列出算式：9+4。在独立思考时，学生可能会有两种方法，一种是把13个桃子一个一个地数完，这类数法蕴含的算理是加法运算的基数意义；另一种是接着9把盒子外面的4个桃子数完，这类数法蕴含的算理则是加法运算的序数意义。

可见，学生在观察情境图的过程中，已经理解了算理，而9+4的算理正是加法运算的意义。在这一直观理解的过程中，学生得到了“9加几”的基础性算法。当然，通过进一步观察情境图，还可以对这样的基础性算法进一步优化，可以想到先拿1个放进盒子，盒内正好是10个桃子，从而总结出“凑十法”。在这个案例中，我们可以发现，教材中的情境图既帮助学生理解了算理，又为算法的孕伏提供了行之有效的原型。

二、知识迁移，孕伏一般性算法

数学学习是一个螺旋上升、循序渐进的过程。学生已经知道什么会直接影响学习效果。所以，在教学新内容时，教师要有意识地激活学生已经拥有的知识经验，灵活运用新旧知识的迁移，帮助学生理解算理，从而实现对算法的构建。

如在教学“两位数乘一位数的笔算”时，教师出示情境图：两只猴，每只采了14个桃。两只猴一共采了多少个桃？在图中，每个猴子采的14个桃分别放在两个筐里，一筐10个，另一筐4个。

学生独立完成时，出现了以下4种做法。

方法1：14+14=28（个）

方法2：10+4+10+4=28（个）

方法3：10+10=20（个）4+4=8（个）20+8=28（个）

方法4：10×2=20（个）4×2=8（个）20+8=28（个）

教师引导学生列出乘法算式：14×2。并追问：14乘2的竖式过程可以怎么写呢？你能尝试着写一写吗？

学生通过对以前算法进行迁移，出现了下面的“一般性”算法：

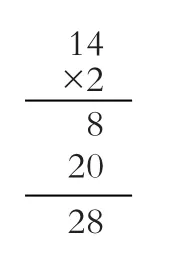
从课堂来看，教师激活了学生已有的认知经验。学生出现的4种方法，本质上都是把所有桃子加起来，但是方法3和方法4能够帮助学生理解14×2笔算方法的算理。学生依据竖式的写法和算理的理解过程，出现了一般性的算法，而这正好为简化两位数乘一位数的竖式过程、规范写法奠定了基础。在该内容的教学中，旧知的掌握促进了算理的理解，同时也为构建算法发挥了支撑性的重要作用。

三、直观操作，孕伏创造性算法

在小学计算教学中，应该加强直观教学，它不仅能够改变课堂的教学方式，变学生被动接受为主动探究，而且能够变算理的抽象表达为直观显示，也为构建算法提供了思维原型。

如在教学“整数除以分数”时，教师课件出示“8块饼干并提出问题：每人吃2块饼干，可以分给几个人呢？每人如果吃1块呢？”

师：你可以用什么方法计算？

生：我可以用除法计算。8除以2等于4人，8除以1等于8人。

（教师接着出示问题）“每人吃2分之一块饼干，可以分给几个人呢？”

师：可以先在图上画一画，再列式算一算。

生2：我也在图上分了分，发现一块饼干可以分给2个人，4块饼干可以分给8人，算式是4乘2等于8人。

师：两位同学说得都有道理。从他们的计算过程，我们也可以发现，不管是4除以，还是4乘2，都得出能分给8人。（边说边板书：4÷=4×2=8）

师：思考每次除以的数和乘的数有什么关系？

学生对于整数除以分数算理的理解，其实从前一个问题就开始了。后一个问题的出现自然实现了整数除以整数向整数除以分数的过渡，而这恰恰是整数除以分数计算的算理。在这个过程中，教师让学生借助直观的饼干图进行操作，使得算理由抽象变得直观，既有助于学生感悟，也蕴含了整数除以分数的计算方法，为学生构建创造性、独特性的算法埋下伏笔。

教育是一门慢的艺术，就像花的盛开，需要经历萌芽—抽枝—含苞—怒放的过程。在计算教学中，教师的教学要遵循学生发展的规律，有时需要以“理”寻“法”，有时需要探“法”悟“理”。恰当把握理解算理与掌握算法的“度”，寻找“理”与“法”的平衡点，就一定可以使“理”“法”相得益彰、和谐联结，使得“理”与“法”成为计算课堂中可以兼得的幸福。

（作者单位：江苏省南京市江宁区土桥中心小学）

（责任编辑：杨强）