高中数学中不等式的证明教学
孙 浩
(江苏省徐州高级中学,江苏 徐州 221000)
高中数学中不等式的证明教学
孙 浩
(江苏省徐州高级中学,江苏 徐州 221000)
不等式的证明是高考考查的重点对象,不等式的证明方法有许多种.文章对不等式的解法进行了一些总结,希望能为读者提供思路,系统地总结了不等式的证明方法.
数学;不等式;证明
高中时期的学习很重要,它决定了你的未来,而高中的学习很大程度上取决于数学的学习.所以教师在教授数学的过程中,应该十分重视,并且在课堂上去利用有限的时间去教授给学生足够多的知识和方法,让学生能够在自己做题的过程中去获得更多的感悟,从而使得他们的数学综合能力得到提升,达到教师教学的目的.当然,教师在进行教学时不应该受到传统教学模式的限制,而是应该根据实际教学情况以及效果去进行改善和创新,以学生的学习情况为基础进行课程的设计和安排,并且在教授中多多创造出新的方法去让课堂的效率更高.
一、巧用情景
学生在学习中应该是处于主体地位,所以教师在进行教学时应该突出学生的主体地位,而情境教学作为可以让学生积极参与的一种教学方式充分体现了学生的主体地位,所以教师在进行数学不等式的教学时应该去联系实际教学情况,并且根据知识点去进行合理情境的设计,让学生能够主动地参与进来,并且去主动地学习相关的不等式知识.当然,教师在设置相关的情境时,需要注意很多问题,包括高中生的心理和生理特点以及题目的难度和情境的联系程度,而其中最重要的一点是,情境学习模式需要学生的积极参与,那么教师在进行情境设计时就应该去培养轻松愉悦的氛围,让学生更容易积极主动地参与进来,并且进行相关章节的学习.
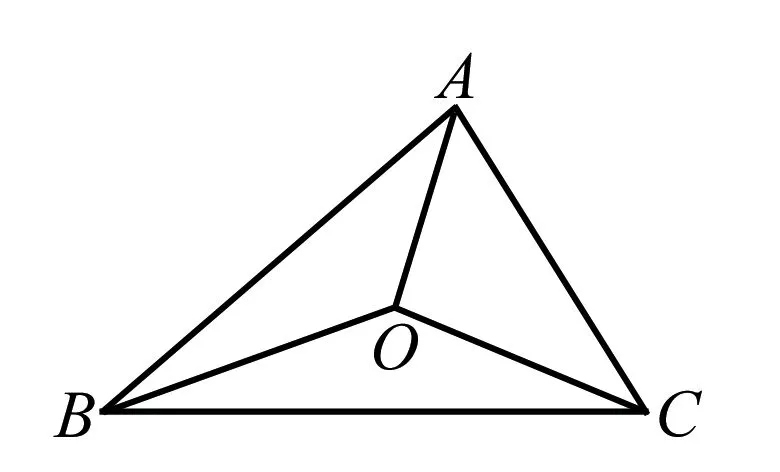
数学不等式问题有很多种类,其中就包括数学证明中的不等式,在此题目中,会涉及到几何中的很多参数,这些参数都是构成数学不等式的一部分,参数的取值不同,就会影响到最终的结果.所以在进行几何问题的不等式教学时就是应该去设置好相关的思路,让学生能够去理解其中的逻辑.如图三角形,AB=AC,O是三角形内部的一点,且∠AOB>∠AOC,证明:OB 在进行数学学习的过程中知识与能力都是不断变化的是动态的,所以教师在进行数学教学时应该注意利用此层次,并且联系学生的思维以及自己的教学策略进行适当的改变,从而让课堂更加高效.当然,教师在进行教学的过程中应该注意教学程度的延伸,也就是说要一步步去提出更深层次的问题,让学生进行思考,从而能够让学生由浅入深地进行学习,使得他们的数学综合能力得以提升.如在教授三角函数的不等式问题时,教师应该从最基本的基础知识去进行延伸,从而使得学生能够更加深入地去理解该种不等式的解题思想以及方法. 教学方法有很多种,教师在进行教学的过程中不应该是一成不变的,而应该根据实际情况去进行创新,好的方法都是在不断的积累中去提出来的,所以教师在进行教学的过程中应该根据实际情况去改变现在的教学方法.例如教师在进行不等式的教学时,可以利用现代的科学技术,去提升学生的思维能力,如多媒体,教师可以将不等式动态地展示在幻灯片中,让学生能够更加清晰地理解题目的思维.当然,除了教学形式的创新还可以进行教学方法的创新. 数学归纳法主要用来证明一些与自然数有关的不等式,数学归纳法作为一种新的教学思维应该备受教师的重视.如当n>1,n∈N时,求证:1/(n+1)+1/(n+2)+1/(n+3)+…+1/(3n)>9/10.证明:当n=2时, 左=1/3+1/4+1/5+1/6=57/60>9/10,假设n=k时,命题成立,即1/(k+1)+1/(k+2)+1/(k+3)+…+1/(3k)>9/10,当n=k+1时,有:左=1/(k+1 )+1/(k+2)+1/(k+3)…+1/(3k)+1/(3k+1 )+1/(3k+2)+1/(3k+3)=﹛1/(k+1)+1/(k+2)+1/(k+3)…+1/(3k)﹜+﹛( 1/(3k+1 )+1/(3k+2)+1/(3k+3)-1/(k+1)﹜ >9/10+﹛( 1/(3k+1 )+1/(3k+2)+1/(3k+3)-1/(k+1)﹜>9/10+3/3(k+1) -1/(k+1)=9/10,不等式也成立. 综上,命题得证. 除此之外,教师还可以利用向量的方法去将不等式向量化,从而使得得出最终结果的效率更加高. 社会在进步,时代在发展,教师在进行教学过程中应该根据实际情况进行教学方法的创新,并且根据学生的反应情况,从而制定下一阶段的教学计划.数学课堂的效率不仅取决于教师还取决于学生,所以教师在教学的过程中应该以学生为主体,并且去联系学生学习的实际情况,设计相应的教学方法,而数学是需要学生的逻辑性和思维性的,所以教师在进行教学的过程中应该去培养学生自主学习的能力,让他们锻炼自己的思维能力.所以教师应该不断提升自身的文化素质和水平,不断的去更新教学理念,并且进行教学方法的创新设计,为学生学习创造一个更好的环境. [1]泽碧啦. 例谈中学数学中不等式的证明方法及技巧[J]. 西藏科技,2012(11). [2]凡仕江. 一个不等式的七种证明方法[J]. 各界文论,2007(02). [3]余志英. 不等式的证明方法[J]. 科学咨询(教育科研),2008(S1). [责任编辑:杨惠民] G632 A 1008-0333(2017)27-0033-02 2017-07-01 孙浩(1983.1-),女,江苏省徐州人,本科学历,中学一级教师,从事高中数学教学研究.二、巧用层次
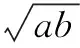
三、巧用创新

