数形结合思想在高中数学教学的效果

王晓兰

(山东省单县第一中学，山东 荷泽 274300)

数形结合思想在高中数学教学的效果

王晓兰

(山东省单县第一中学，山东 荷泽 274300)

高中数学教学对学生的要求较高，如何化难为简、深入浅出的教学值得教学工作者进行深入的探究.数学思想对学生学习效率的提升意义较大，以数形结合思想为例，在高中数学教学中进行数形结合思想的应用及渗透可以很好地提升学生的数学能力，有利于学生多角度解题思维的形成.以下本文将简单分析数形结合思想，重点围绕数形结合思想在高中数学教学中的效果及应用策略展开详细论述.

数形结合思想；高中数学；应用策略；效果

1.数形结合思想

数学教学中的数与形都十分关键，将数与形结合在一起既可以达到知识点的相互交融与渗透，同时还可实现一加一大于二的作用，这对于减轻高中学生学习难度优势较为突出，在同一解题要求下，通过图形分析可以很好提炼出所需的数据，同样，借助数据也可绘制出符合题目要求的图形，从虚与实之间的变化过程中，学生的数学能力也会得到相应的提升.无论是以数解形还是以形解数其本质都是协助主体进行解题，数形结合思想自身具备的化难为简、变抽象为具体的强大优势值得教师进行实践与创新.

2.数形结合思想的意义

数学知识相较于语言类学科而言，较为抽象，而数学思想则可发挥出纽带作用将其联系起来，形成较为完整、条理清晰的数学知识链，因而在各阶段的数学教学中，数学思想教学及渗透都在持续的进行中.数形结合思想在高中数学教学中应用较为普遍，通过数与形之间的转换能够发挥出化难为易的作用，并在较短的时间内帮助学生进行解题，这对于高中数学教学而言意义重大.

3.应用策略

(1)借助多媒体进行数形结合的渗透

信息化是当代教学的重要标志，在高中数学教学中，教师可以通过多媒体技术进行教学创新，帮助学生在动态化的教学演练中形成数形结合意识，拓宽学生的数学思维.

(2)加速教学生活化的转变

学以致用是进行各科教学的主要目标，教学生活化可以更好地帮助学生明白学习的意义，真正发自内心地爱上学习.高中数学教学抽象性突出，部分学生认为很多知识点与生活无关，因而学习起来非常的被动和吃力，通过生活化的教学，教师可以帮助学生建立起正确的学习观，自发积极地爱上数学教学.

(3)数、形的结合应用

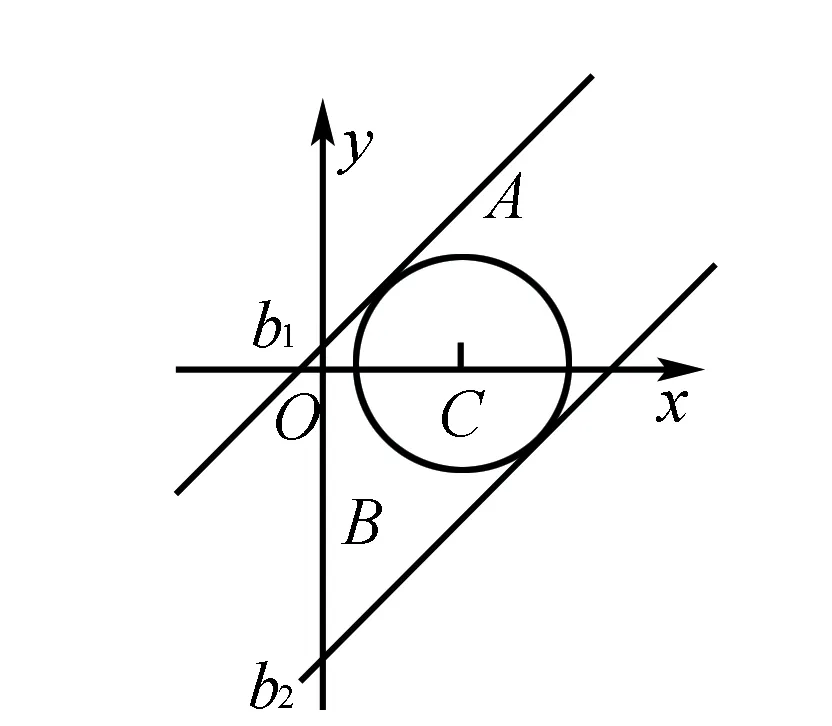
一般而言，在高中数学教学中应用数形结合思想方法，主要在一次函数、二次函数、三角函数等解题应用，同时，直线、圆锥曲线图形可以充分表达一些代数变化，对解题有着一定的帮助作用.比如，点M(x，y)是圆(x-2)2+y2=3上的任意一点，求x-y的最小值与最大值.

解析设x-y=b，可以将此方程转变为y=x-b，将直线与圆相切，那么-b就是直线在y轴上的截距，如上图所示，b1就是x-y的最小值，b2就是x-y的最大值.

数形结合思想对学生解题能力的培养及强化十分有利，通过数与形之间的转换，学生可以更深层次地了解数学知识的内在关联，这对于学生个人能力的提升及良好学习思维的养成大有裨益，需要教师从主观意识上予以重视，并将其与实践相结合，真正地发挥出答疑解惑的优势作用，为社会培养出更多综合能力较强的高素质人才.

[1]彭再云,唐平.数形结合思想在高考数学中的应用浅析[J].教育教学论坛,2013(50).

[2]张小军.例谈高中数学数形结合解题法教学的有效策略[J].高中数理化,2013(20).

[责任编辑：杨惠民]

G632

A

1008-0333(2017)27-0020-01

2017-07-01

王晓兰(1983.6-)，女，山东省荷泽人，中学二级教师，本科，从事高中数学教育教学.