高中数学教学中学生创造性思维的培养

李容君

(江苏省盐城市田家炳中学,江苏 盐城 224000)

高中数学教学中学生创造性思维的培养

李容君

(江苏省盐城市田家炳中学,江苏 盐城 224000)

高中数学教师培养学生创造性思维的方法为应用开放性习题解放学生的思想，应用具有转换思维的习题让学生学会联想，布置典型的非常规习题打破学生的思维定势，应用这样的方法，教师可培养学生的创造性思维.

高中；数学；学生；创造性；思维

学生的创造性思维水平影响着学生的解题水平.如果学生具有创造性的思维，就能从多种角度看问题，得到最多解决问题的方法.高中数学教师要在教学中培养学生的创造性思维，开展这种教学有非常重要的意义.

当幼苗长到三叶时要及时用石磙镇压，蹲苗以促进根系生长，增加分蘖，使幼苗生长健壮。镇压时，选择晴天的下午，此时苗发软，损伤轻。

一、应用开放性习题，培养学生的发散思维

部分学生没有创造性的思维，是因为学生的思维被限制在课本中、教师教授的知识中、权威的教学答案中，这类学生不敢有思想，也不愿意有思想.当学生只能机械地记知识，不能够用自己的脑筋去思考知识的时候，又如何能有创造的思维？如果教师希望学生能有创造的思维，就应为学生创造一个可以自由思考的平台，让学生能够在学习中思考，使学生自由地发散思维.

以数学教师引导学生学习习题1为例.

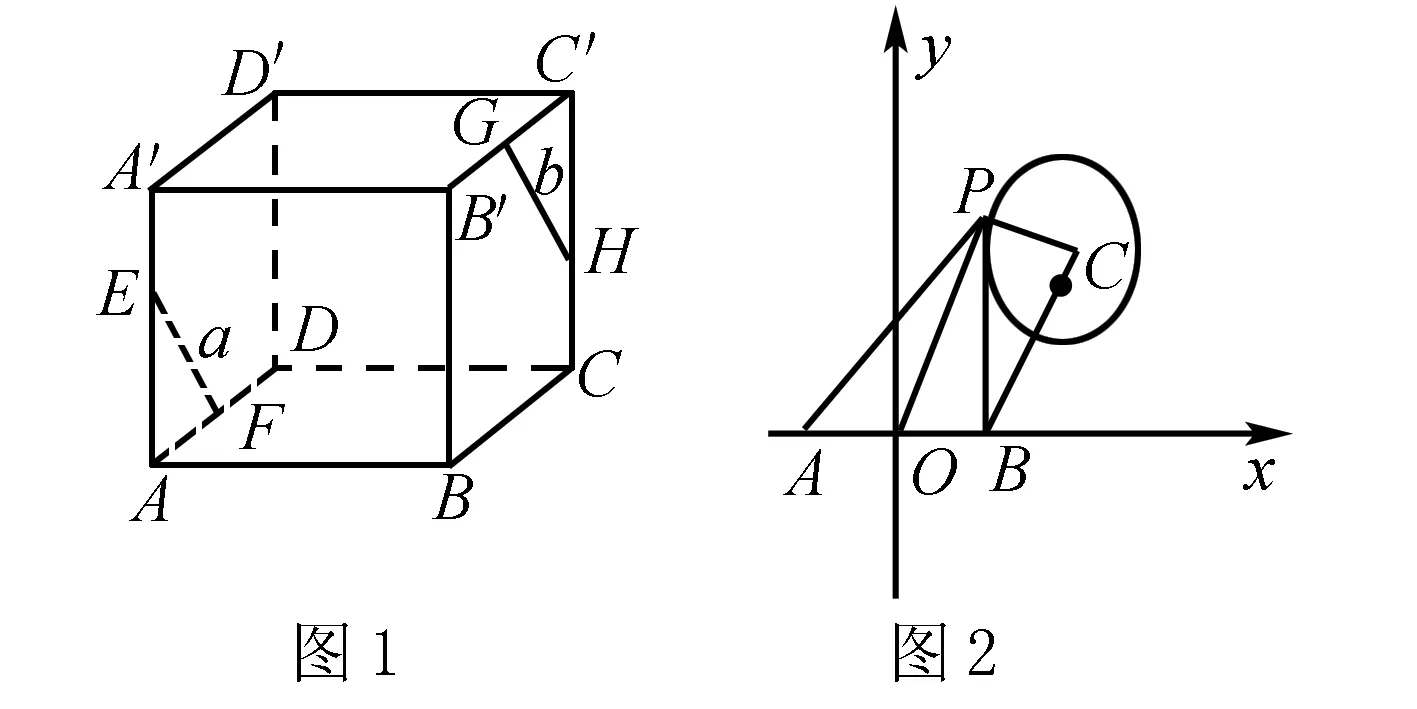
习题1 如图1，设直线a，b在正方体不同的两个平面内，如果现在要求a∥b，那么还需要添加什么已知条件才成立？

习题1是一个开放题.过去教师在教授概念的时候，会告诉学生课本上的数学概念是什么意思，这些数学概念应该怎么用.当学生习惯了被灌输知识的学习方法以后，便不会愿意再主动地思考知识.现在教师给学生做开放题，学生在做习题1的时候，会产生一种想法：现在如果要让a∥b，需要应用到什么性质呢？如果学生要了解这个答案就要自主地阅读课本.当学生完成了答案之后，学生需要再思考，数学性质是可以延伸和变化的，现在这一题的答案只有一个吗？如果不是，第二个与之相关的数学性质是什么呢？学生在做开放习题的时候，便会形成自主思考、自主探索的数学习惯，从而发散思维逐渐形成.

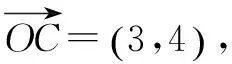
二、应用性质的比较，培养学生的联想思维

当学生遇到问题的时候，只会用常规的思路来思考问题，思维就会受到限制.常规的思路是指学生结合条件来思考答案，从因推到果来思考问题.假如学生能够应用非常规的思维来看问题呢？学生会发现数学有另一片新天地.

习题2 已知定点A(-1,0)和B(1,0)，点P是圆(x-3)2+(y-4)2=4上的一动点，求|PA|2+|PB|2的最大值和最小值.

当学生具备了发散思维以后，学生需要了解要以什么为依据进行发散.数学知识的体系非常广，如果学生找不到数学发散的方向，可能就会漫天发散，找不到探索问题的方向.联想思维是一种把两件相似的事物联系起来，对比思考的思维方式，数学教师可以引导学生应用联想思维的方式找到发散的方向.

教师如果要培养学生的创造性思维，就要为学生布置典型的开放性习题，引导学生一边做题一边探索知识、一边发散知识.当学生不再被动地学习知识，学会自主思考的时候，发散的思维便能形成.

㉒参见 Kopp，Verwaltungsgerichtsordnung Kommentar，19．Aufl．，2013，1Rn．34a．

教师在培养学生的创造性思维时，要培养学生的联想思维能力，即引导学生找到数学问题的结合点，把一个问题的性质变成另一个问题的性质.如果学生具备这种以相似点为核心，由此及彼的思维方法，就能用更加宏观的视角看问题，应用创造性的思维看待问题.

三、应用非常规案例，培养学生的探索思维

现用教师引导学生学习习题2为例.

教师可以引导学生做习题2，刚开始的时候，学生应用几何的计算方法，会觉得这道题的解法特别繁复，并且解题条件还不完全.教师可以引导学生思考，如果不把习题2这个几何问题当作几何问题，而当作向量的问题呢？当学生把习题2这一几何问题变成向量问题的时候，便发现这道题简单得多了.在完成这一次的学习以后，学生意识到了在遇到一个数学问题的时候，不能孤立地看待数学的性质，学生要应用发散的思维，把数学性质和数学性质结合起来思考，比如一个几何问题可以是一个函数问题，可以是一个不等式问题，也可以是一个向量的问题，只有不局限于一个问题的性质，才能拓宽解题的视野.

随着社会发展和科技进步，标准化的基本概念也在逐渐发生变化，尤其是进入近代标准化阶段。这个阶段的特点是：社会化大生产为标准化理论演进提供了大量生产实践经验和总结，科学技术也为之提供了技术手段和实验方法，突破了仅靠零散总结经验的直观表述阶段，使标准化活动进入了科学的定量化阶段，并要求在民主协商的原则下推行应用，从而大范围地提高生产率。[1]

在林业的发展过程当中，要想实现林业的可持续发展，则需要不断优化林业的经济结构，对其进行合理分配，具体表现在以下方面。其一，加强对短期林木的培育管理，实施速生林建设，以最短的时间内实现林业的经济价值，为林业经济效益的提升发挥其重要的作用。其二，基于科技发展的背景下，加大新品种的研发，实现资源的合理优化配置，淘汰低效率的产品，实现资源重组。其三，延伸林业产业链。根据当前森林资源面临的形式，建立以森林为依托的旅游发展产业，增加林业产品的附加值。合理调整林业产品不合理的结构，增加对其科技投入，提高林业产品的科技含量，实现林业经济效益的最大化。

在第三学段，6个版本中，知识点个数为8~9，均含有Z1、Z6、Z7、Z8、Z10、Z11、Z12、Z13这8个知识点．除人教版的“性质5（是中心对称图形）”知识点处于九上外，其它5个版本的平行四边形内容均处于八下．对于“性质5（是中心对称图形）”知识点，北师版、冀教版和苏教版将其编写在“平行四边形的性质和判定”之前，在呈现该知识点的同时，还把它作为探究发现或论证平行四边形性质的手段；其它3个版本，则将其编写在“平行四边形的性质和判定”内容之后．

现以教师引导学生学习习题3为例.

习题3 在(0,2π)内，使sinx>cosx，那么x的取值范围应是( ).

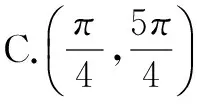
结合图9、图10可以得到，方铅矿具有较好浮选回收率的矿浆电位区间与元素硫存在的电位-pH区间大致重合，这是因为在此区间内生成的元素硫具有良好的疏水性，从而提高了方铅矿浮选回收率。当矿浆电位过低时，溶液具有强还原性，此时硫元素会被还原成亲水性的两性离子HS-，使矿物疏水性减弱，回收率降低。当矿浆电位过高时，溶液呈强氧化性，会生成PbO，形成亲水钝化层[8]，同样会影响方铅矿浮选，使回收率降低。

因为π不属于选择A、B、D的数值，它只属于C，于是可以先用π这一数值验证答案，经计算可知，x=π时，条件成立，于是C是正确的.因为它是个单选题，所以A、B、D均为错误的答案.

教师可以引导学生看到，在习题3中，学生从因推到果，从条件推到答案找解题的途径，这一方法是行不通的，如果应用常规的方法来思考问题，这一题的已知条件不全.然而如果学生结合题目的特殊性来思考呢？这一题给出了四个答案，其中有一个正确的答案，学生是不是可以把答案放到条件中试，验证出答案？这是一种很好的解题方法.假如现在答案过于抽象，那是不是可以在抽象的答案范围中估出一个特殊的取值，比如在这一题中，选取一个只满足于C，不满足于其它答案的特殊数值来验算答案，通过排除错误的答案来找到正确的答案？这一题也证明这是一种很好的解题思路.

教师要引导学生能跳出常规思维，解合解题的需求，结合生活实践创造出解题的方法.只要学生能跳出常规思维局限，能用逆向思维、特例思维等方式来思考问题，就会发现可以应用多种角度来思考问题，从而能创造出新的解题策略.

[1]李田梅,才智. 中学数学教学中培养学生创造性思维能力探析[J].2015(12).

[2]王俊松.浅谈中学生数学创新思维的培养[J]. 中国校外教育,2012(20).

[责任编辑：杨惠民]

G632

A

1008-0333(2017)27-0025-02

2017-07-01

李容君(1981.3-)，女，江苏盐城人，中学一级教师，大学本科，从事高中数学教育.