TOPSIS算法在高职院校院系办学质量评价中的应用

林 敏

(武汉职业技术学院， 湖北 武汉 430074)

TOPSIS算法在高职院校院系办学质量评价中的应用

林 敏

(武汉职业技术学院， 湖北 武汉 430074)

本文根据TOPSIS算法的原理及步骤给出了高职院校院系办学质量评价的方法.

高职院校；TOPSIS算法质量评价

一、问题提出

近年来，我国高职教育得到了迅猛发展，为进一步推动高职教育的发展，我国启动了国家示范性高职院校建设项目，旨在通过示范性院校建设，推动各校的办学实力，办学水平和办学质量的提高，建成一批世界先进水平的高职院校.为此各高职院校也对本校各院系办学质量提出了要求，如何提高各院系的办学质量是不容忽视的问题.为了客观地评价各院系办学的实际状况，学校组织过一次校内各学院的评估.为了取得经验，我们随机抽取了五个院系进行试评估.下表给出的是5所院系的评估数据：

表1

要求根据以上表格提供的数据对5所院系的办学质量进行评价.

二、TOPSIS算法的原理

TOPSIS法是一种逼近于理想解的排序法，这种方法通过检测评价对象与最优解、最劣解的距离来进行排序，若评价对象最靠近最优解同时又最远离最劣解，则为最好，否则为最差.即按照靠近正理想解和远离负理想解的程度，来对方案进行排序，从而选出最优方案.

设方案集为D={d1,d2，…，dm}，衡量方案优劣的属性变量为x1,…,xn，这时方案集D的每个方案di(i=1,…，m)的n个属性值构成的向量是[ai1,ai2，…，ain]它作为n维空间中的一个点，能唯一地表征方案di.正理想解C*是方案集D中并不存在的虚拟的最佳方案，它的每个属性值都是决策矩阵中该属性的最优值；而负理想解C0则是虚拟的最差方案，它的每个属性值都是决策矩阵中该属性的最差值.在n维空间中，将方案集D的每个方案di与正理想解C*和负理想解C0的距离进行比较，既靠近正理想解又远离负理想解的方案就是方案集D中的最优方案.

三、TOPSIS算法的步骤

(2)求加权规范矩阵C=(cij)m×n.设由决策人给定各属性的权重向量为ω=[ω1,ω2,…,ωn]T,则：cij=ωj·bij,i=1,2,…,m;j=1,2,…,n.

(4)计算各方案到正理想解与负理想解的距离.备选方案di到正理想解的距离为：

备选方案di到负理想解的距离为：

(5)计算各方案的综合评价指数，即

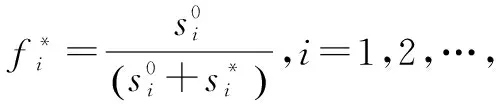
四、院系办学质量评价求解方法

第一步：数据预处理

2.生师比既非效益型属性又非成本型属性，属于区间型属性，这种区间型的属性采用以下方法进行处理:

生师比x2处理后的生师比130.5241351480.4520

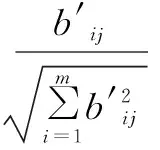
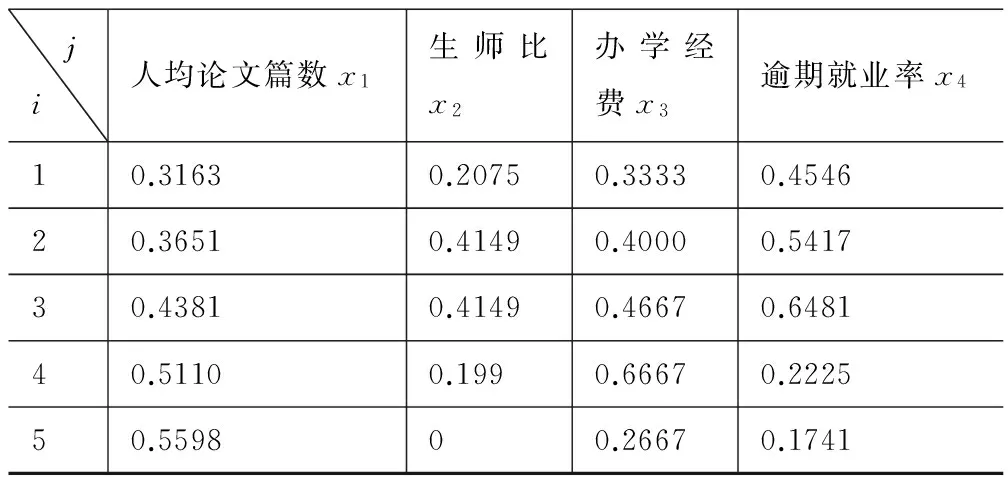
表1 的数据经规范化后的属性值

第二步：设权向量ω=[0.2,0.3,0.4,0.1]，得到加权的向量规范化属性值如下表：

表2

第三步：由表2可知

正理想解C*=[0.1196,0.1248,0.2667,0.0174],

负理想解C0=[0.0632,0,0.1067,0.0648].

院系名称S*iS0if*i10.14790.18210.551820.12190.18750.606030.10180.17180.627940.12000.18190.602550.24020.07450.2367

[1]姜启源.数学模型(第三版)[M].北京：高等教育出版社,2003.

[2]陈理荣.数学建模导论[M].北京：北京邮电大学出版社,1999.

[3]齐欢.数学模型方法[M].武汉：华中理工大学出版社，1996.

[4]司守奎，孙玺菁.数学建模算法与应用[M].北京：国防工业出版社，2011.

[责任编辑：杨惠民]

G632

A

1008-0333(2017)27-0022-02

2017-07-01

林敏(1975.8-)，女，汉族， 湖北黄陂人， 硕士，副教授,从事数学教育.