水平表面气流剪切作用下的水膜厚度

冷梦尧， 常士楠， 丁亮， 李晓峰

北京航空航天大学 航空科学与工程学院， 北京 100083

水平表面气流剪切作用下的水膜厚度

冷梦尧， 常士楠*， 丁亮， 李晓峰

北京航空航天大学 航空科学与工程学院， 北京 100083

飞机结冰表面上的液态水受气流吹拂作用会发生向后溢流，从而影响结冰区域范围及防冰系统设计；为了获得水膜流动规律，对水平平板表面上气流剪切驱动的水膜流动进行了实验测量和建模分析。通过水膜流动风洞试验台产生高速气流驱动水膜的流动，使用色散共焦位移计测量同一位置的水膜在不同时刻的厚度变化，结果表明气-液界面由底层薄水膜和多种尺度的波动组成，具有变化速度快随机性强的特点。通过水膜厚度随气流速度及水膜雷诺数的变化规律，发现平均水膜厚度与两者均呈现出单调非线性的依赖关系。基于薄水膜流动理论和平均水膜厚度实验结果，提出了高速气流剪切作用下的气-液波动界面剪切因子计算式，适用于风速17.8～52.2 m/s，水膜雷诺数26～128之间的平板水膜流动计算。

飞机防冰； 两相流； 水膜厚度； 界面剪切力； 建模

当飞机穿过含有过冷水滴的云层时，其迎风表面会迅速覆盖积冰，严重威胁飞行安全。在不完全冻结或湿态防冰过程中，表面存留的液态水会在气流驱动下向后流动，改变飞机表面水的分布范围，形成冰角或溢流冰脊；水膜表面上的波动反过来会干扰气流边界层的流动，对结冰或防冰表面的热量及其分布造成影响。而水膜厚度方向上的导热对于结冰预测或防冰热流计算也是必不可少的一项。故研究飞机表面水膜流动对于冰形模拟及防冰系统优化设计是十分有意义的。

在理论和数值仿真方面，经典的Messinger模型[1]首先在飞机结冰预测中考虑液态水的存在，但该模型假设当前控制体内未冻结的水即全部进入下一个控制体。Ai-Khalil等[2]则通过对水膜的稳定性分析发展了防冰表面溢流模型。Myers和Thompson[3-4]基于润滑近似理论建立水膜流动方程，提高了水膜模型的物理意义，随后该模型进一步被应用于结冰理论[5-6]、防冰及溢流冰的模拟[7-8]中。Fortin等[9]则根据机翼表面的近距离摄像观察结果，根据粗糙表面换热模型研究液态水带来的影响。还有部分研究者专注于水膜表面波动的形成和发展[10-12]。然而这些模型大都是同宏观结果进行对比验证，对于水膜流动过程中的部分物理机制缺乏了解，导致预测结果仍有一定误差。

近几年，随着实验观测技术的发展，研究飞机表面液态水流动机理的实验逐渐增多，例如加速流场中的水珠脱离临界条件[13]，水珠受力情况及运动规律[14]，溪流厚度的空间特征研究[15]等，这些实验结果完善了飞机表面水珠及溪流形态的液态水流动机制。关于连续性水膜的研究，Feo和Tsao[16]为建立明冰缩比理论测量了驻点附近的水膜厚度，并建立其同模型尺寸、液态水含量、水滴直径以及风速之间的关系。Muzik等[17]观察了水膜在翼型表面上的流动特征及破碎现象。Zhang 等[18]使用数字图像投影技术(Digital Image Projection, DIP)测量了翼型表面的水膜厚度，得到水膜厚度约在10～1 000 μm之间，但未建立起有效的水膜厚度与外部条件之间的关系。

本文针对高速气流驱动的水膜流动进行了测量，并根据实验数据建立起水膜流动方程。通过搭建特定的水膜观测实验台在平板表面产生连续性流动的水膜，使用色散共焦位移计记录一段时间内水膜厚度的时域信号，分析水膜形态随风速及水流量的变化规律。根据平均水膜厚度实验结果，结合由Myers模型推导的水平稳态膜厚计算式，拟合出气-液波动界面剪切系数计算式，并通过与无量纲水膜厚度文献结果对比进行验证。

1 水膜流动方程

已有实验结果表明[5,18]，飞机表面存在的水膜厚度极薄且流速较低，故而可将水膜简化为二维不可压缩层流流动。又由于水膜温度变化区间较窄，认为水膜物性参数(密度和黏度)为常数，假设表面外法向坐标为n，切向坐标为s，法向速度为v，切向速度为u，水膜连续性方程及二维不可压缩稳态Navier-Stokes方程可表达为

(1)

(2)

(3)

式中：ρw为水的密度；μw为水的黏度；p为水膜内压强；g为重力加速度。由于水膜厚度方向上的尺寸为微米级，相对于流向长度而言，可以忽略不计，即n≪s。可应用润滑近似理论[4]对动量方程考虑以下简化：① 忽略表面法线方向速度，即认为v=0；② 结合连续性方程可忽略速度u的切向变化，即∂u/∂s=0。简化后得到动量方程分别为

(4)

(5)

根据式(5)可知，水膜内压强的法向梯度是由重力造成的，压强p在水膜厚度方向上成线性分布。分别在气-液交界面和液-固边界应用以下边界条件[4]：① 压强和界面切应力连续；② 无滑移平整边界，对式(4)和式(5)先后求积分可得

p=p∞(s)+ρwgn(n-h)

(6)

(7)

式中：τ为界面剪切应力；h为当地水膜厚度；p∞(s)为气流边界层底部的压强，当气流与水膜流动均处于充分发展阶段，空气压力沿切向变化很小[6]，可认为∂p/∂s～0。将速度沿法向积分可求得水流量的计算式为

(8)

为便于得到水膜表面剪切力的影响规律，本实验关注在水平平板表面上的水膜流动，重力切向分量ρgs等于零，气流剪切力成为水膜流动的关键影响因素，得到相应的水膜厚度为

(9)

分析式(9)可发现，液体黏度由水膜的温度计算得到，而水流量Q取决于局部撞击水量及上游流入的水量，故而气-液界面剪切力τ的大小成为了求解水膜厚度的关键因素。Alzaili和Hammond[5]采用流场求解得到的壁面剪切应力作为τ的值，但是显然气-液界面上的波动会大大增强两相之间的相互作用。借鉴气-液两相分层流研究的经验，界面剪切力可以表示为[10,19]

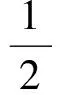
(10)

式中：fi为界面剪切系数；ρa为空气密度；Ua为空气主流速度。界面剪切系数fi通过实验结果测得，并可表达为水膜雷诺数的函数，即fi=f(Ref)。水膜雷诺数定义为Ref=Q/Wνw，W为水膜湿润宽度，νw为液体运动黏度。而C则为气-液界面波的相位速度。一方面，由于界面波动的速度远小于主气流速度，故而在式(10)中往往将其忽略[20-22]。另一方面，气-液界面波的相位速度同样取决于风速Ua和水膜雷诺数Ref[23]，即C=f(Ua,Ref)。本文在做实验数据处理时亦采用忽略波动速度C的简化式。

2 试验装置

水膜厚度测量在北京航空航天大学防/除冰系统研究实验室的小型风洞中进行，如图1所示。高速气流由离心风机提供，经稳定段整流、收缩段加速后进入实验段中。试验段承力结构为不锈钢，底部中间安装抛光铝板作为实验底板，表面粗糙度平均为0.19 μm，平衡接触角为70°。实验段顶部及左右侧面使用透明亚克力玻璃板粘接制成，其中顶部中间段设计可拆卸，方便观测仪器的安装和调节。实验段顶部距底板50 mm，横向宽200 mm，总长0.5 m。风速由皮托管风速计在位移计测量点附近测得，主气流的速度范围为0～55 m/s，横截面上风速均匀区可达76%。

观测所使用的水源为纯净水，由离心水泵驱动，经由供水箱从底部进入试验段。供水箱使用疏水性的有机玻璃材料制成，有助于稳定水流，并增强水箱口的密封性。供水口为距试验段入口约55 mm的长缝，且其下游侧面边缘倒有圆角。在试验底板末端留有出水口，以吸水性材料填充，回收的这部分水流会再进入循环中。此外，高风速大流量试验中会有小水滴被卷吸脱离水膜表面，并随气流从风洞扩压段的出口离开，而这部分水不再进入水流循环。

水膜的厚度使用色散共焦位移计(ACR-HNDS100)测量和记录。该位移计由一个控制器和一支光笔组成，通过感测从物体表面反射回来的单色光波长，将波长换算获得相应距离值，若反射回两个波长即可得到被测物的厚度值。位移计被安装在水流出口下游245 mm的位置，试验过程中与被测物之间的距离保持在其焦距(40 mm)附近，数据采集频率为2 000 Hz，每个试验点采集20 000组数，每组试验至少重复三次。所有试验均在常压室温条件下进行，并待空气及水流运行稳定一段时间后再测量。试验风速范围为17.8～52.2 m/s，水膜雷诺数在22～138之间，在此范围内水膜可以均匀地铺展在铝板表面。

图1 试验装置
Fig.1 Test setup

3 结果与分析

3.1 水膜厚度的瞬态特性

试验状态点及典型水膜厚度时域图分别绘于图2、图3和图4中。尽管水膜厚度时域信号随风速和水流量的变化是一个连续的过程，仍可参考气-液两相分层流动的流域划分方式[22]，将其分为三维波(3D)、滚动波(Roll-wave)以及卷吸(Entrainment)3种不同的流动区域。三维波区域内的界面波具有振幅小且频率高的特点，且界面波随着底部黏性水膜层一起运动，相位速度低。当供水流量增大时，黏性底层不足以输运全部液体，在三维波动之上出现了振幅较大、移动速度更快的滚动波。滚动波由于特殊的运动方式而得名，其瞬态信号具有相位速度快、随机性强的特点，水膜表面波的追赶与合并也都发生在此区域内。卷吸区发生在流量大且风速高的条件下，波动顶部的液体被气流卷吸脱离水膜表面。在本文试验中，风速高于36.5 m/s、水膜雷诺数大于89时能够观察气流中夹带水滴的现象，然而从水膜厚度时域图难以区分滚动波与卷吸区域。

本文使用Ishii和Grolmes[24]提出的理论对试验中发生的卷吸现象进行简要分析，图2展示了室温条件下本文试验条件与Ishii和Grolmes的空气-水两相流动卷吸判别式的对比。点A实验条件为Ua=30.5 m/s 且Ref=38，点B实验条件为Ua=30.5 m/s 且Ref=128。Ishii和Grolmes根据界面受力分析以及不稳定理论建立了卷吸现象的临界判别式，因此可不受两相流流道形状和尺寸的影响。气液两相流中的卷吸现象产生的机理按水膜雷诺数划分为3种方式：根切(Undercut)，滚动波剪切(Roll-wave breakup)以及粗糙湍流(Rough turbulent)。由图2可知现试验中的卷吸现象主要为滚动波剪切作用，即当气流剪切力大于水膜表面张力时，滚动波顶部在气流剪切作用下发生变形直至断裂形成水滴，故而主要发生在高风速大流量的试验点。考虑到水膜对飞机防冰的影响来自存留在表面上的部分，且试验点大都未达卷吸雾化核心区，故而只关注表面水膜厚度自身的变化。

图2 试验状态点及与文献[24]卷吸判别式的对比
Fig.2 Test points and comparison with Ref.[24]entrainment criteria

图3 气流速度U=30.5 m/s，不同供水流量下的水膜厚度时域图
Fig.3 Instantaneous thickness of water film with different liquid flow rates under wind speed U=30.5 m/s

图4 水膜雷诺数Re=89，不同风速下的水膜厚度时域图
Fig.4 Instantaneous thickness of water film with different wind speeds under liquid Reynolds number Re=89

比较同一风速下不同供水流量的水膜厚度时域图的变化情况(图3)可以发现，水膜表面滚动波的频率随着水膜雷诺数的增加而逐渐增大，同时基底水膜及滚动波振幅则无明显变化。相对而言，从图4可以看出，当风速发生变化时，基底水膜厚度及滚动波的频率和振幅都有较大变化。这表明，高速气流是水膜表面波动行为的主导因素。由Kelvin-Helmholtz不稳定性理论[22,24]可知，当上下分层的两个不同流体之间存在速度差时，流体界面会产生扭曲，两流体之间发生位置和动量的交换，即界面波动现象。由于较轻的气体在上层，较重的液体在下层，当速度差较小时界面波动在水膜表面张力和重力的作用下得到抑制，而当两者速度差增大到一定程度后，界面不稳定情况加剧，下层液体交换获得更高的动量，直至克服自身黏性力形成涡旋，即滚动波。若只增大水流量，相间相对速度没有太大变化时，则界面变形情况较为相似，只是滚动波发生的频率提高以承载更多的液体输运量。

3.2 平均水膜厚度及预测模型

图5 平均水膜厚度随风速和水膜雷诺数的变化规律
Fig.5 Variation of mean film thickness with different wind speeds and film Reynolds numbers

另一方面，在风速较小的条件下，水膜雷诺数Ref的变化对平均水膜厚度的影响更大，这是由于气流对表层水膜的加速作用较弱，上层水膜与底层水膜的速度差小，增加水流量后水膜厚度即迅速增加。当风速提高后，水膜厚度随Ref的变化速率随之降低。而在水膜流动进入卷吸区时，还可看到水膜厚度变化趋势发生轻微的偏转，表明卷吸现象进一步削弱了水膜雷诺数对膜厚的影响。

fi=0.106Ref-0.133

(11)

图6 界面剪切系数试验结果及拟合曲线
Fig.6 Test data and correlation for interfacial shearfactor

值得注意的一点是，本文拟合结果发现界面剪切因子随着水膜雷诺数的增大而减小，这与水流量的增加引起波动增加从而增强剪切作用的常规认识相反。随后可见在分层流Ref=100前后也表现出类似的规律[19]。这是由于在剪切力计算式中忽略了界面波相位速度的缘故，即水流量增加时，波的相位速度C也会相应增大。而通过将风速及水流量对波动相位速度的影响分别并入剪切力和界面剪切系数的计算式中，并不影响最终水膜厚度计算式。

在关于飞机表面的水膜流动计算方面，文献中最终推导得到水平表面水膜厚度计算式的形式大都同式(9)一致[4-5,10-11]，而界面剪切力的计算主要应用了以下两种方式：① 近似认为外流场求解得到的壁面摩擦应力等于气-液界面剪切力τ；② 假设管内气-液两相流与平板水膜流动规律相同，使用管内流界面应力公式计算τ。本文使用这两种方法得到界面剪切系数fi，并分别代入水膜计算式中，将预测结果与实验结果进行了对比，如图7所示。具体计算方法如下：

1) 平板边界层模型[25]

假设界面剪切系数等于半无限大平板湍流边界层摩擦因子cf，则其计算式为

fi=cf=0.074(Rea)-0.2

(12)

式中：气流雷诺数Rea=UaL/νa，其中νa为空气运动黏度，L为特征长度，此处取值为试验段高度。

2) Cheremisinoff分层流模型[19]

将Ref=100作为小振幅界面波流域及滚动波流域的划分，可得界面剪切系数计算式为

(13)

从图7(a)中可以看出，由于水平壁面摩擦系数显著小于气-液波动界面剪切系数，由此计算出来的水膜厚度远高于试验值。由于壁面摩擦系数是在气流掠过光滑固壁表面上得到的，没有考虑气-液界面波动对于空气流场边界层的影响，这也符合水膜表面波动能够增强对气-液交互作用的结论。而图7(b)中表明使用管内分层流动经验式计算的界面剪切力同样偏小，这是由于原试验中气流速度较低(<20 m/s)，且流道底面的内凹形状令水膜向底部聚集，这样得到的水膜厚度比平板上的试验结果偏大。另外，本文所使用的固壁基底材质为亲水性的金属铝，而文献中的流道基底材质为有机玻璃，表面特性的不同也可能对结果带来一定的影响。而使用本文的界面剪切系数公式计算得到的平均水膜厚度，与试验结果相比误差约在20%以内。

图7 平均水膜厚度试验值与各剪切因子模型预测值的对比
Fig.7 Comparison of mean film thickness test value with results from different shear factor prediction models

与经典的无量纲水膜厚度经验式的对比，可验证本文所得的界面剪切力计算方法的正确性。在环状气-液两相流的研究中，通常认为液体流量，平均膜厚及液膜剪切应力三者符合“三角关系式”，即知道其中任意两者的值后可确定剩余一项的值。液膜无量纲厚度δ+将平均水膜厚度与剪切应力相结合进行去量纲化，随后即可表达为无量纲液体流量Ref的函数。δ+的定义为

(14)

(15)

表1中列出了文献及本文的无量纲水膜厚度计算模型，各模型的计算值同实验值的比较结果如图8所示。对比发现使用本文提出的剪切力计算式对平均水膜厚度实验数据进行无量纲化后，与Kosky & Staub根据水平冷凝环状流研究提出的计算模型最为相符。基于逆向竖直环状流实验提出的Hughmark模型在水膜雷诺数较小的范围内与本试验结果符合的较好，但在水流量较大的部分产生明显差异；而基于竖直向下环状流的Asali模型反映出的无量纲水膜厚度随Ref的变化规律与试验结果相似，但δ+的值整体更小。

表1无量纲水膜厚度关系式及应用范围

Table1Dimensionlessfilmthicknessrelationandtheirapplicationrange

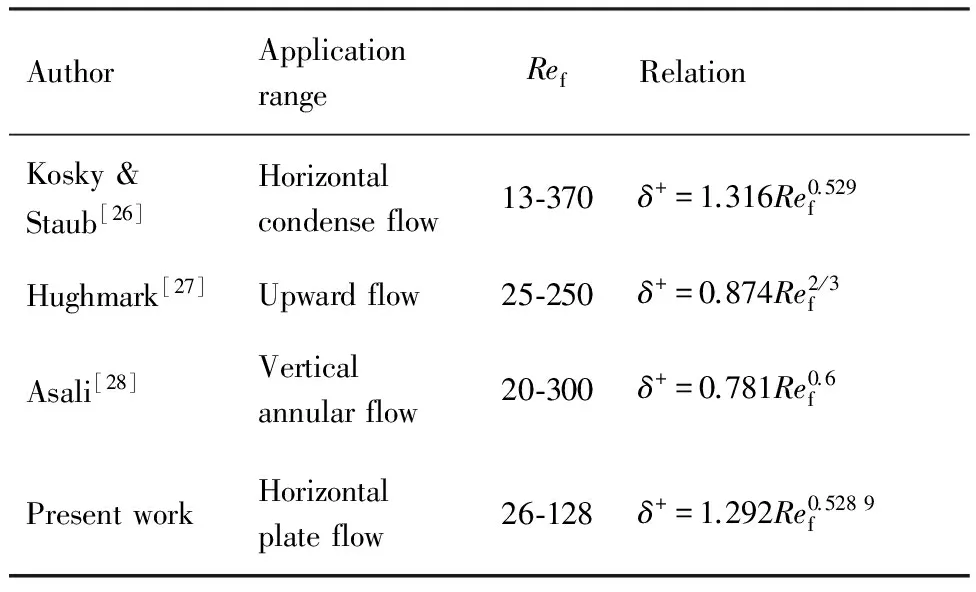
AuthorApplicationrangeRefRelationKosky&Staub[26]Horizontalcondenseflow13⁃370δ+=1．316Re0．529fHughmark[27]Upwardflow25⁃250δ+=0．874Re2/3fAsali[28]Verticalannularflow20⁃300δ+=0．781Re0．6fPresentworkHorizontalplateflow26⁃128δ+=1．292Re0．5289f

图8 无量纲水膜厚度与各模型预测结果的对比
Fig.8 Comparison of dimensionless water film thickness with results from different prediction models

4 结 论

针对飞机表面结冰及防冰过程中水膜流动计算和预测的需求，对高速气流驱动的水膜流动进行了试验研究，分析了水膜厚度瞬态特征随气流速度及水流量的变化规律，对水膜厚度时域平均值进行统计，校验了使用平板边界层模型或管内分层流模型的膜厚计算方法，并应用新的界面剪切系数计算式实现平均水膜厚度的准确预测。研究发现：

1) 高速气流驱动下的水平平板水膜流动，按界面波动特征可分为三维波、滚动波及卷吸区3种流动区域，且这3种流域之间存在一个平缓变化的过程。

2) 平均水膜厚度随气流速度的减小或水膜雷诺数的增大而增大。增大气流速度时，水膜表面小波动的频率显著增加，滚动波的振幅和频率则有降低；而相同风速下，水膜雷诺数的增大主要表现出滚动波频率的增大。

3) 常见的外流场边界层模型，或低风速分层流动中总结得到的经验关系式应用于气液两相界面上出现剧烈的波动时，水膜厚度预测结果与实验数据的偏差较大。由此可见，界面剪切应力的准确模化是获得准确水膜厚度的前提和基础。

[1] MESSINGER B L. Equilibrium temperature of an un-heated icing surface as a function of air speed[J]. Journal of the Aeronautical Sciences, 1953, 20(1): 29-42.

[2] AI-KHALIL K M, KEITH T G, DE-WITT K J. Development of an improved model for runback water on aircraft surfaces[J]. Journal of Aircraft, 1994, 31(2): 271-278.

[3] MYERS T G. Extension to the Messinger model for aircraft icing[J]. AIAA Journal, 2001, 39(2): 211-218.

[4] MYERS T G, THOMPSON C P. Modeling the flow of water on aircraft in icing conditions[J]. Journal of Aircraft, 1998, 36(6): 1010-1013.

[5] ALZAILI J, HAMMOND D. Experimental investigation of thin water film stability and its characteristics in SLD icing problem[C]//SAE 2011 International Conference on Aircraft and Engine Icing and Ground Deicing. Chicago: SAE International, 2011.

[6] DU Y X, GUI Y W, XIAO C H, et al. Investigation on heat transfer characteristics of aircraft icing including runback water[J]. International Journal of Heat and Mass Transfer, 2010, 53(19-20): 3702-3707.

[7] WRIGHT W B, STRUK P, BARTKUS T,et al. Recent advances in the LEWICE icing model[C]//SAE 2015 International Conference on Icing of Aircraft, Engines, and Structures. Prague: SAE International, 2015.

[8] HARIRECHE O, VERDIN P, THOMPSON C P, et al. Explicit finite volume modeling of aircraft anti-icing and de-icing[J]. Journal of Aircraft, 2008, 45(6): 1924-1936.

[9] FORTIN G, LAFORTE J, ILINCA A. Heat and mass transfer during ice accretion on aircraft wings with an improved roughness model[J]. International Journal of Thermal Sciences, 2006, 45(6): 595-606.

[10] KAREV A R, FARZANEH M, LOZOWSKI E P. Character and stability of a wind-driven supercooled water film on an icing surface—I. Laminar heat transfer[J]. International Journal of Thermal Sciences, 2003, 42(5): 481-498.

[11] UENO K, FARZANEH M. Linear stability analysis of ice growth under supercooled water film driven by a laminar airflow[J]. Physics of Fluids, 2011, 23(4): 042103.

[12] WANG G K, ROTHMAYER A P. Thin water films driven by air shear stress through roughness[J]. Computers & Fluids, 2009, 38(2): 235-246.

[13] WHITE E B, SCHMUCKER J A. A runback criterion for water drops in a turbulent accelerated boundary layer [J]. Journal of Fluids Engineering, 2008, 130(6): 061302.

[14] 孟繁鑫, 朱光亚, 李荣嘉, 等. 加热表面水珠运动特性研究[J]. 航空学报, 2014, 35(5): 1292-1301.

MENG F X,ZHU G Y, LI R J, et al. Study of water drop motion characteristics on heating surface [J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(5): 1292-1301 (in Chinese).

[15] MOGHTADERNEJAD S, JADIDI M, NABIL E, et al. Shear driven rivulet dynamics on surfaces with various wettabilities[C]//ASME 2014 International Mechanical Engineering Congress and Exposition. Montreal: American Society of Mechanical Engineers, 2014.

[16] FEO A, TSAO J. The water film weber number in glaze icing scaling[C]//2007 SAE Aircraft and Engine Icing International Conference. Seville: SAE International, 2007.

[17] MUZIK T, SAFARIK P, TUCEK A. Analysis of the water film behavior and its breakup on profile using experimental and numerical methods[J]. Journal of Thermal Science, 2014, 23(4): 325-331.

[18] ZHANG K, WEI T, HU H. An experimental investigation on the surface water transport process over an airfoil by using a digital image projection technique[J]. Experiments in Fluids, 2015, 56(9): 173.

[19] CHEREMISINOFF N P, DAVIS E J. Stratified turbulent-turbulent gas-liquid flow[J]. AIChE Journal, 1979, 25(1): 48-56.

[20] ANDRITSOS N, HANRATTY T J. Influence of interfacial waves in stratified gas-liquid flows[J]. AIChE Journal, 1987, 33(3): 444-454.

[21] PARAS S V, VLACHOS N A, KARABELAS A J. Liquid layer characteristics in stratified—Atomization flow[J]. International Journal of Multiphase Flow, 1994, 20(5): 939-956.

[22] TZOTZI C, ANDRITSOS N. Interfacial shear stress in wavy stratified gas-liquid flow in horizontal pipes[J]. International Journal of Multiphase Flow, 2013, 54(3): 43-54.

[23] SETYAWAN A, INDARTO, DEENDARLIANTO. The effect of the fluid properties on the wave velocity and wave frequency of gas-liquid annular two-phase flow in a horizontal pipe[J]. Experimental Thermal and Fluid Science, 2016, 71(4): 25-41.

[24] ISHII M, GROLMES M A. Inception criteria for droplet entrainment in two-phase concurrent film flow[J]. AIChE Journal, 1975, 21(2): 308-318.

[25] 吴望一. 流体力学(下册)[M]. 北京： 北京大学出版社, 2004: 370-386.

WU W Y. Fluiddynamic (Part 2)[M]. Beijing: Peking University Press, 2004: 370-386 (in Chinese).

[26] KOSKY P G, STAUB F W. Local condensing heat transfer coefficients in the annular flow regime[J]. AIChE Journal, 1971, 17(5): 1037-1043.

[27] HUGHMARK G A. Film thickness, entrainment, and pressure drop in upward annular and dispersed flow[J]. AIChE Journal, 1973, 19(5): 1062-1065.

[28] ASALI J C, HANRATTY T T, ANDREUSSI P. Interfacial drag and film height for vertical annular flow[J]. AIChE Journal, 1985, 31(6): 895-902.

(责任编辑： 李明敏)

URL：www.cnki.net/kcms/detail/11.1929.V.20161027.1057.002.html

Thicknessofwaterfilmdrivenbygasstreamonhorizontalplane

LENGMengyao,CHANGShinan*,DINGLiang,LIXiaofeng

SchoolofAeronauticScienceandEngineering,BeihangUniversity,Beijing100083,China

Liquidwateronthesurfaceofaircraftwillrunbackundertheeffectoftheairflow,resultinginredistributionoficeaccretionandanti-icingheatflux.Experimentalmeasurementandmodelinganalysisareconductedtoinvestigatetheflowbehaviorofshear-drivenwaterfilmonthehorizontalflatsubstrate.Thewaterflowfilmisdriveninawindtunnel,andtheinstantaneousthicknessismeasuredinthesamelocationusingalaserfocusdisplacementmeterbasedonconfocalchromatictechnique.Itisfoundthattheinterfacebetweenthegasandliquidphasesconsistsofunderlyingthinfilmandmultiplescalefluctuations.ThevariationrelationshipofthefilmthicknessbetweenthewindspeedandfilmReynoldsnumberisalsoobtained.Resultsshowthattheaveragefilmthicknessdependsmonotonicallyonthesetwofactors.Basedonfilmflowmodelandexperimentaldata,anewcorrelationforcalculatingtheairshearstressaboveathinfilmisproposedandvalidatedbycomparisonwithpreviousstudies.Thecorrelationcanbeappliedforwaterfilmthicknesscalculationoverarangeofwindspeed(17.8-52.2m/s)andwaterfilmReynoldsnumber(26-128).

aircraftanti-icing;two-phaseflow;waterfilmthickness;interfacialshearstress;modeling

2016-08-23；Revised2016-09-18；Accepted2016-10-25；Publishedonline2016-10-271057

NationalBasicResearchProgramofChina(2015CB755803)

.E-mailsn_chang@buaa.edu.cn

2016-08-23；退修日期2016-09-18；录用日期2016-10-25； < class="emphasis_bold">网络出版时间

时间：2016-10-271057

www.cnki.net/kcms/detail/11.1929.V.20161027.1057.002.html

国家“973”计划 (2015CB755803)

.E-mailsn_chang@buaa.edu.cn

冷梦尧， 常士楠， 丁亮， 等． 水平表面气流剪切作用下的水膜厚度J． 航空学报,2017,38(2):520696.LENGMY,CHANGSN,DINGL,etal.ThicknessofwaterfilmdrivenbygasstreamonhorizontalplaneJ.ActaAeronauticaetAstronauticaSinica,2017,38(2):520696.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0275

V211; O359.1

A

1000-6893(2017)02-520696-09