多视角探析、拓展2017年江苏卷解析几何题*

●

(大厂高级中学,江苏 南京 210044)

多视角探析、拓展2017年江苏卷解析几何题*

●陈业代

(大厂高级中学,江苏 南京 210044)

高考试题对日常的教学方式和训练方式有着举足轻重的影响． 认真探析高考试题是十分必要的，它能指导我们有序复习、有章可循、有法可循; 研究拓展高考试题，既能提升教师专业技能，又能提高高三复习效率．

多视角; 探析; 拓展; 反思

2017年江苏省数学高考遵循了《新课程标准》和《江苏高考考试说明》，立足课本，注重双基，考查能力，充分体现能力立意的命题原则.其中的解析几何题改变以往的大运算量，注重对学生基础知识、基本运算能力的考查，问题背景熟悉，内涵丰富，是一道值得从多视角探析和拓展的好题.

1 尝试改进参考答案，多视角探析高考试题

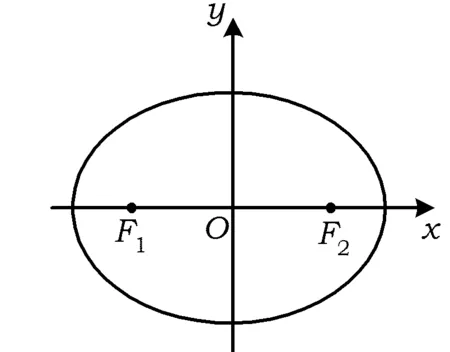
图1

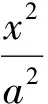
1)求椭圆E的标准方程；

2)若直线l1，l2的交点Q在椭圆E上，求点P的坐标.

(2017年江苏省数学高考试题第17题)

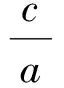
解得a=2,c=1，于是

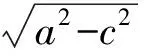
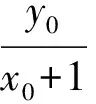
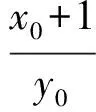
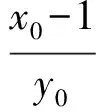
联立直线l1，l2的方程可得

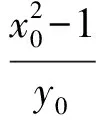
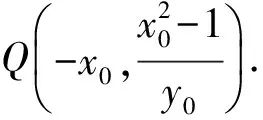
点Q在椭圆上，由对称性得

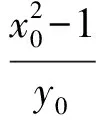
即

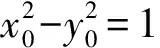
又点P在椭圆E上，从而

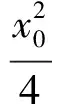
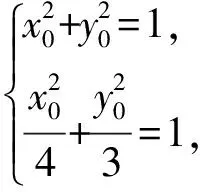
评注第1)小题是常规求椭圆问题，第2)小题也是常规的思路，但学生可能会忘记考虑直线PF1,PF2斜率不存在的情形，容易丢分.

笔者思考的问题是：1)能不能对此方法加以改进，回避讨论斜率不存在的情形？2)能否对这道高考题进行拓展？经过多次思考与尝试，现将探究整理如下(以下解法2和解法3中，第1)小题同解法1，对第2)小题的解法进行了适当改进)：

1.1 回避讨论，探析真题

解法22)由第1)小题知，F1(-1,0)，F2(1,0),设P(x0,y0)，x0>0,y0>0，Q(x1,y1).由PF1⊥QF1,PF2⊥QF2,得

两式相减得

x1=-x0，

从而

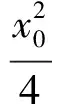
方程组无实数解.若y0=y1，则

由x0>0,y0>0，得

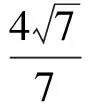
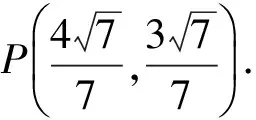
评注通过向量数量积回避斜率不存在讨论，但在运算量上与参考答案方法差不多，怎样更简单些呢？于是就有下面的探究.

1.2 借助平面几何知识，探究真题

解法32)根据PF1⊥QF1,PF2⊥QF2,即∠PF1Q=∠PF2Q=90°，得4个点P,F1,F2,Q在以PQ为直径的圆上.设P(x0,y0)，x0>0,y0>0，Q(x1,y1),则圆的方程为

(x-x0)(x-x1)+(y-y0)(y-y1)=0.

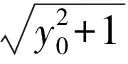
当然，考虑到运算量问题，本题还可作如下改进：借助平面几何知识，由PF1⊥QF1,PF2⊥QF2,即∠PF1Q=∠PF2Q=90°,得4个点P,F1,F2,Q共圆.设圆心为C，则点C既在PQ上又在y轴上，若设P(x0,y0),x0>0,y0>0，则C(0,y0)，⊙C的方程为

点P可看作⊙C与椭圆E的一个交点，由

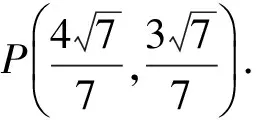
评注对于解析几何问题，学生往往困惑在方法选择上，经常出现要么想出方法算不出结果，要么根本想不到最佳方法，思维的长度决定了运算量的大小.

2 改编试题，创新求解

这道高考题主要考查直线与椭圆的位置关系，根据两条直线交点及点在椭圆上，通过方程组思想求解，对中等学生来说是一道容易题.这难道是对这几年江苏省高考解析几何解答题因难而得分不理想的一个“补偿”吗？于是引起了笔者的兴趣，想对本题作一些改编尝试.

2.1 改算为证，强化基础

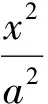
1)求椭圆E的标准方程；

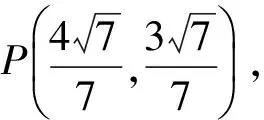
分析1)略.

2)根据PF1⊥QF1,PF2⊥QF2和F1(-1,0),F2(1,0),得直线QF1的方程为

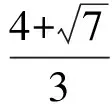
直线QF2的方程为

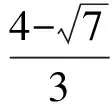
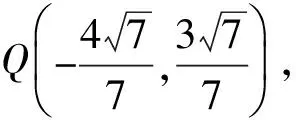
评注改编后思维量减小，运算直接，考查了解析几何运算的基本技能.

2.2 改变思维长度，突出运算能力

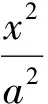
1)求椭圆E的标准方程；

2)若点F2关于直线PF1的对称点Q在椭圆E上，求点P的坐标.

分析1)略.

2)由第1)小题可知c=1，因为点F2关于直线PF1的对称点Q在椭圆E上，所以

|F1Q|=|F1F2|=2.

设Q(x1,y1)，则

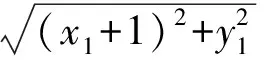
又点Q在椭圆上，则

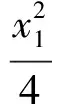
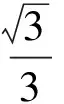
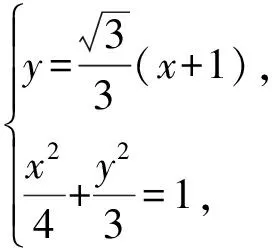
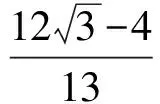
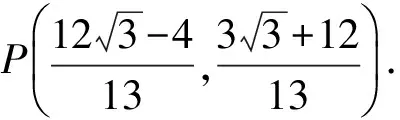
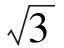
2.3 横向拓展，命题一般化

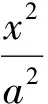
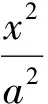
2.4 纵向拓展，创新求解

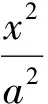
分析设P(x0,y0)，x0>0，y0>0,Q(x1,y1),椭圆焦距为2c.由PF1⊥QF1,PF2⊥QF2,得

两式相减,得

x1=-x0，

从而

即

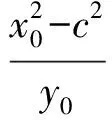
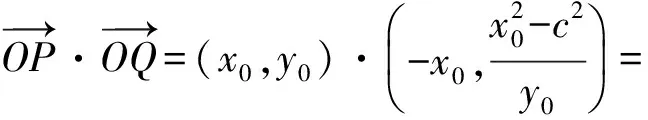
-c2=b2-a2(定值).

评注静止是相对的，运动是绝对的，数学因运动而不再枯燥，数学因运动而充满活力.变式5告诉我们动中有静，运动是有规律的，只要我们认真探索，就能掌握其规律.

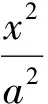
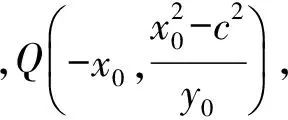
因为点P在椭圆上，所以

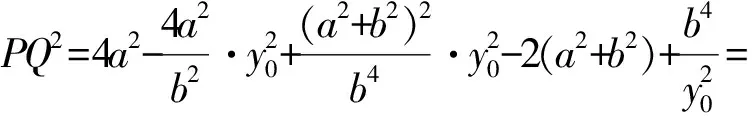
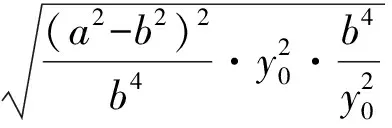
4(a2-b2)=4c2,

即

PQ≥2c,

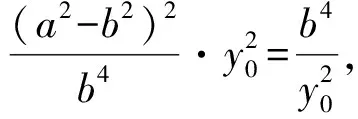
因此，当b2c，点Q在以点P为圆心、2c为半径的圆外.

评注变式5、变式6的改编来源于点Q坐标的结构特征，从数字到字母，学生运算起来比较吃力.在教学中，教师适当地对典型试题作一些变式训练，会让学生的思维更开阔，对提高学生的基本能力也有很大帮助.

2.5 类比联想，触类旁通

从变式5、变式6的解析过程可看出，变式5、变式6的结论在双曲线中仍然成立.

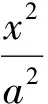
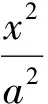
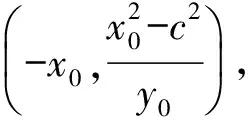
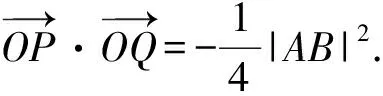
3 反思提高

近几年江苏省数学高考对解析几何大题的命制越来越趋于理性，结构越来越简洁，很好地控制了难度系数，给予学生充分的想象空间，让运算更合理，考查数学核心素养;探析和拓展高考试题，指导高三教学方向，注重基础，加强理性思维的训练，淡化特殊技巧，加强针对性，指导学生学会分析问题，学会选择方法解决问题.

高三教学要以教材为本，按照知识的逻辑顺序开展系统、全面地复习，帮助学生系统掌握基础知识、基本技能和基本方法，形成明晰的知识网络和稳定的认知结构.以《高考说明》为方向，认真研究近几年国内的高考试题，把握命题规律与趋势，切口要小，研究要深，可采用微专题挖掘和研究，让学生学会探寻数学问题的源与流，搞清楚数学思想方法的来龙去脉，做到融会贯通，建构方法网络，让高三复习效率最大化.

2017-07-28

陈业代(1968-)，男，江苏仪征人,中学高级教师.研究方向：数学教育.

O123． 1

A

1003 - 6407(2017)11-39-04