借鉴拓展性课程 编制拓展类试题*
●
(金华市教育局教研室,浙江 金华 3210017)
借鉴拓展性课程编制拓展类试题*
●傅瑞琦
(金华市教育局教研室,浙江 金华 3210017)
初中数学拓展性课程,旨在促进学生数学素养的进一步形成和个性化的发展. 通过一道中考试题的编制,探讨如何基于拓展性课程设计理念,在真实的生活情景中,发现数学问题,设置考查方向,实现对学生建模能力、探究能力和创新能力等数学素养的考查.
拓展性; 试题编制; 思考
初中数学拓展性课程,属于知识拓展类,包括学科的研究性学习、专题教育等,旨在拓展学生的知识面,激发学生的学习兴趣,突出课程的兴趣性、活动性、层次性和选择性,促进学生数学素养的进一步形成和个性化发展.
这种理念如何在中考命题中体现呢?着眼于对“数学素养”的考查,需要有问题情景、思考过程来体现数学思想.在真实的生活情景中,发现数学问题,让学生运用所学知识,进行分析、合情推理,体现对学生建模能力、探究能力和创新能力等数学素养的考查.现以2016年浙江省金华市数学中考卷选择题第9题的命制过程,来探讨如何运用拓展性课程理念来设计试题.
1 素材选择
根据试卷双向细目表,选择题的第9题(共10题)难度系数目标为0.75~0.85之间,设计为几何操作探究类问题,选择学生熟悉的学习背景,抽象几何图形,借助学生学习经验的积累,把操作、观察、探究融合在一起,来考查学生的几何直观.为此,笔者选择一智力游戏,作为命题研究的素材.
智力游戏有5个同学站在操场上,其中没有3个人在同一直线上,也没有4个人在同一个圆周上.请找出3个同学用一根绳子围成一个圆,使得剩下的两个同学,一个在圆内,一个在圆外.
操作过程如图1,这5个同学分别站在点A,B,C,D,E,分两步分析:1)易找到点A,B,使得其他3个点在AB的同侧,则3个角∠ACB,∠ADB,∠AEB必然都不相等.若有角相等,则角的两个顶点与A,B在同一圆上,不符合题意.2)不妨设∠ACB>∠ADB>∠AEB,如图2,选中间大小的角的顶点D,作出过点A,B,D的⊙O,则点C在该圆内,点E在该圆外.
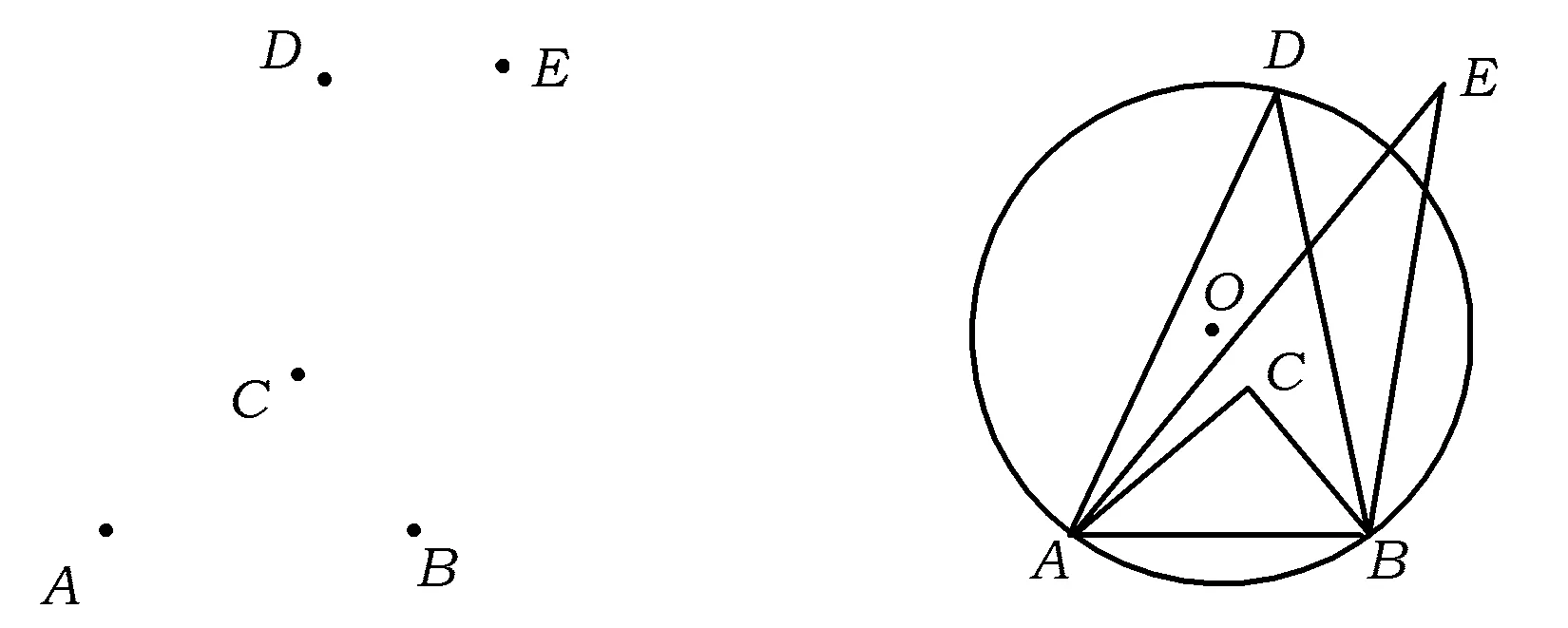
图1 图2
2 素材分析
这是浙教版《数学》九年级上册第3章“圆的基本性质”的拓展性学习内容.解决此题可联系圆的相关知识,利用“不在同一直线上的三点确定一个圆”,作出⊙O,利用“圆外角小于圆周角、圆内角大于圆周角”这一性质,可以判定这样作图的合理性.
此素材联想了足球运动,如图2,如果把AB看成球门,点D,C,E为射点,仅从射门角大小考虑,最佳的射点为点C.因此,联想足球场上的进攻与防守,容易抽象出几何问题,有广阔的创造空间,是拓展性课程设计的重要资源,从球员带球线路的方向、守门员出击防守等视角去研究足球运动,联系对应的数学知识,让学生经历以“操作、发现、猜想和验证”为活动主线的问题探究过程.在一个崭新的背景中,关注建模能力,可以考查学生对知识的应用能力,达到适度区分的目的.
3 成稿研究
方案1如图3,AB为球门,当球员沿EF方向进攻时,在EF上的点E,F,G,H中,仅考虑射门角,射点最好的位置是
( )
A.点EB.点FC.点GD.点H
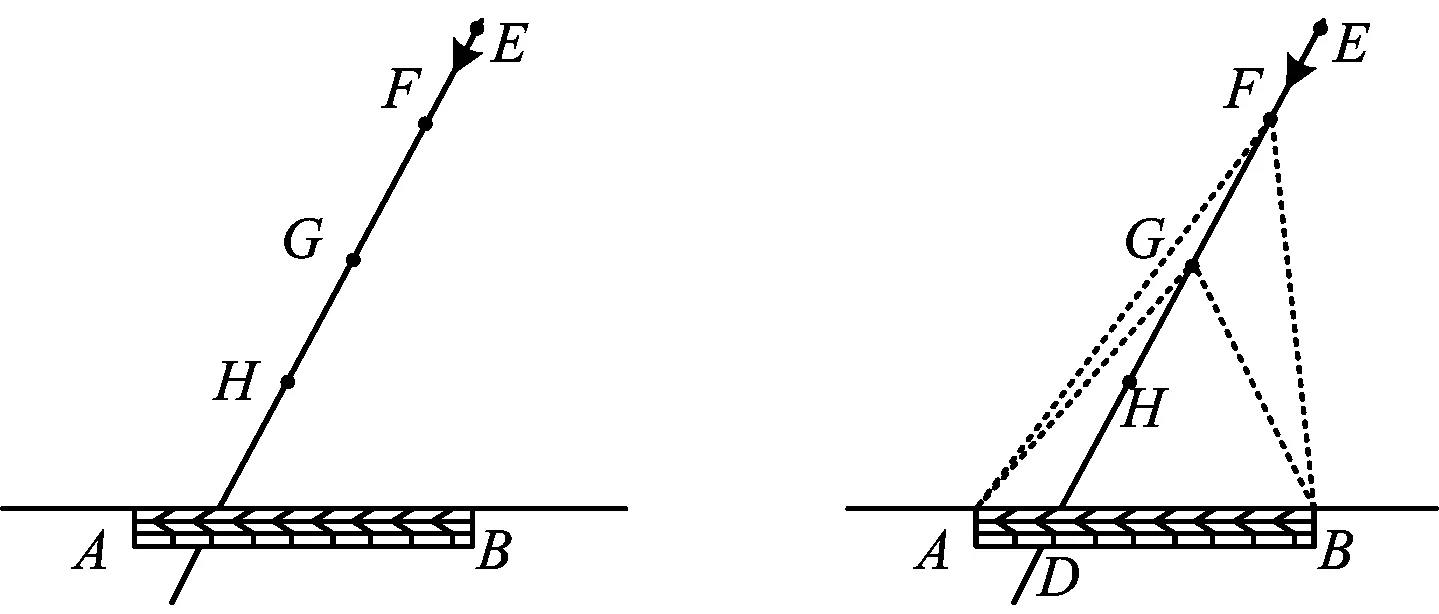
图3 图4
分析利用“三角形外角大于不相邻的一个内角”,如图4,联结GA,GB,FA,FB.在△AGF中,∠AGD>∠AFD;在△BGF中,∠BGD>∠BFD,从而
∠AGD+∠BGD>∠AFD+∠BFD,
即
∠AGB>∠AFB,
同理可得 ∠AHB>∠AGB>∠AFB>∠AEB,
因此射点在点H处射门角最大.
但是,该方案考查的知识点只有“三角形外角大于不相邻的一个内角”,比较单一,如果学生用量角器等工具量一下,就绕过了对此知识的考查.为此,加入三角函数等相关内容,从运球的方向角度设计问题.
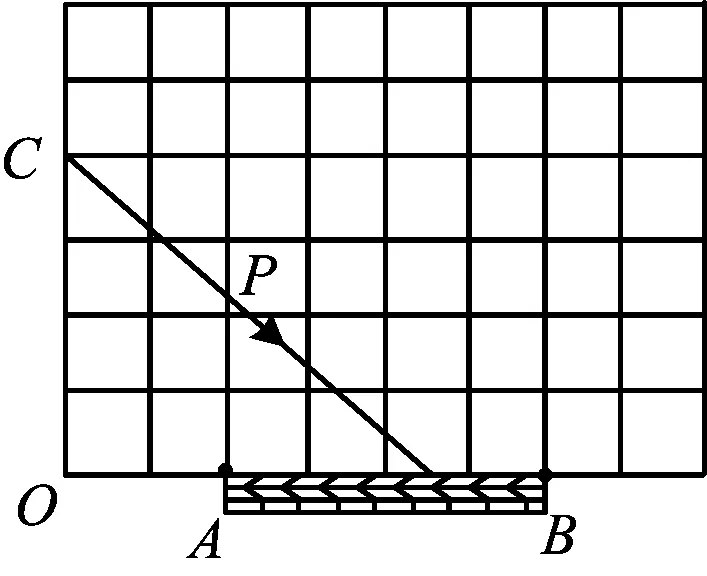
图5
方案2在如图5所示的正方形网格中,点A,B在格点处,球从格点C处沿CP方向进攻,CP上的点离球门越近就越好,设∠OCP=α,tanα=t,则t的范围是
( )


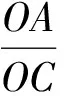
另外,方案1也说明了一个事实,即足球进攻路线与球门AB有交点时,离球门AB越近就射点越好.如果没有交点,那么又可以从哪些角度去设计问题?尝试“最近路程”联系相关知识,设计问题进行研究.
方案3在如图6所示的正方形网格中,小正方形边长为a,CD为运球路线,球门AB中点M为格点,则点M到CD的最近距离是
( )
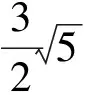
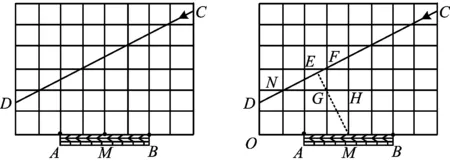
图6 图7
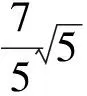
方案4在如图6所示的正方形网格中,小正方形边长为a,守门员从门柱点A跑出阻拦足球,在DC上的点P处将球击飞后跑回球门柱B,当守门员跑的路程最小时,则该路程是
( )
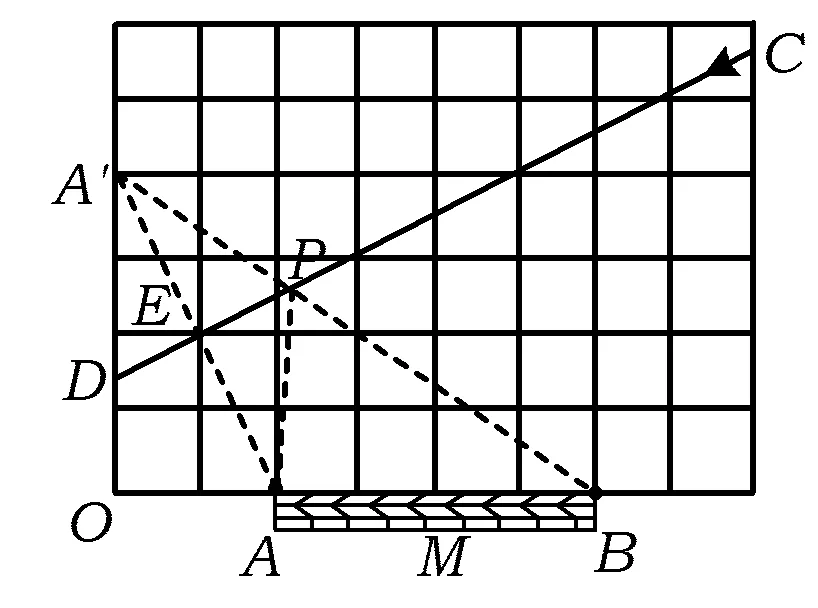
图8
A.10aB.15a
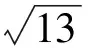
如图8,联结AE,则AE⊥CD,点A′与点A关于CD对称.联结A′B,则A′B与CD的交点即为点P,最短的路程
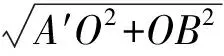
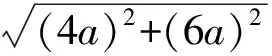
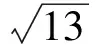
这两个方案都是利用相似三角形的性质构造CD的垂线,再应用勾股定理求得相关线段的长.方案3应用的是垂线段最短原理;方案4则是应用轴对称性质作对称点找最近路线,知识联系综合度合适,但较常规,创新力度不够.
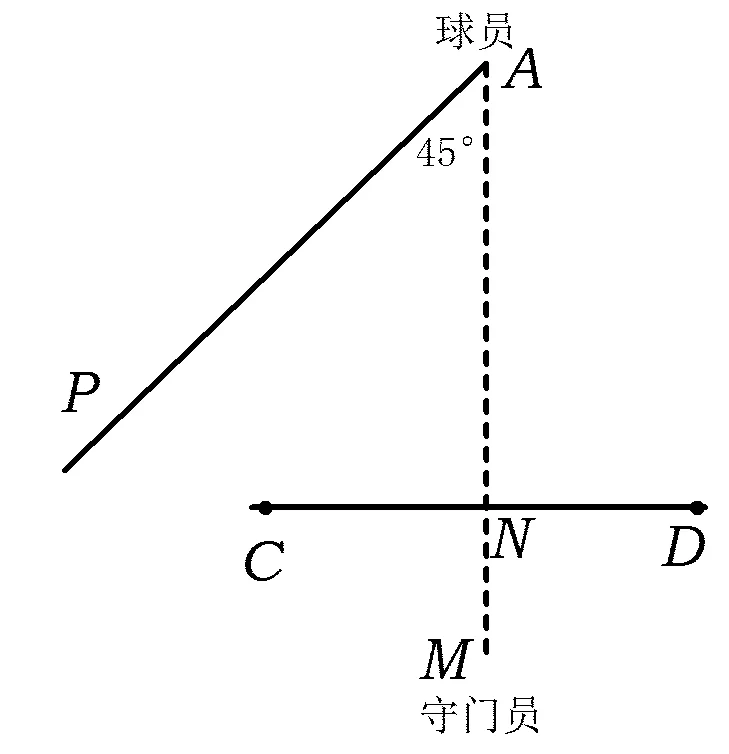
图9
方案5如图9,如果在球门AB前站一排人墙CD,球员从点A沿AP直线带球进攻,有∠MAP=45°,AM为人墙CD的中垂线.若AM=20a,CD=16a,点M到CD的距离6a,那么守门员从点M出发绕过人墙,在射线AP上拦截足球的最近路程是
( )


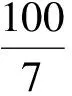
正确的作图是:联结CM,再过点C作CH⊥AP于点H,如图11,则MC+CH即为拦截足球的最近路程.求解时,只要延长NC交AP于点G,在Rt△CNM中,
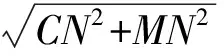


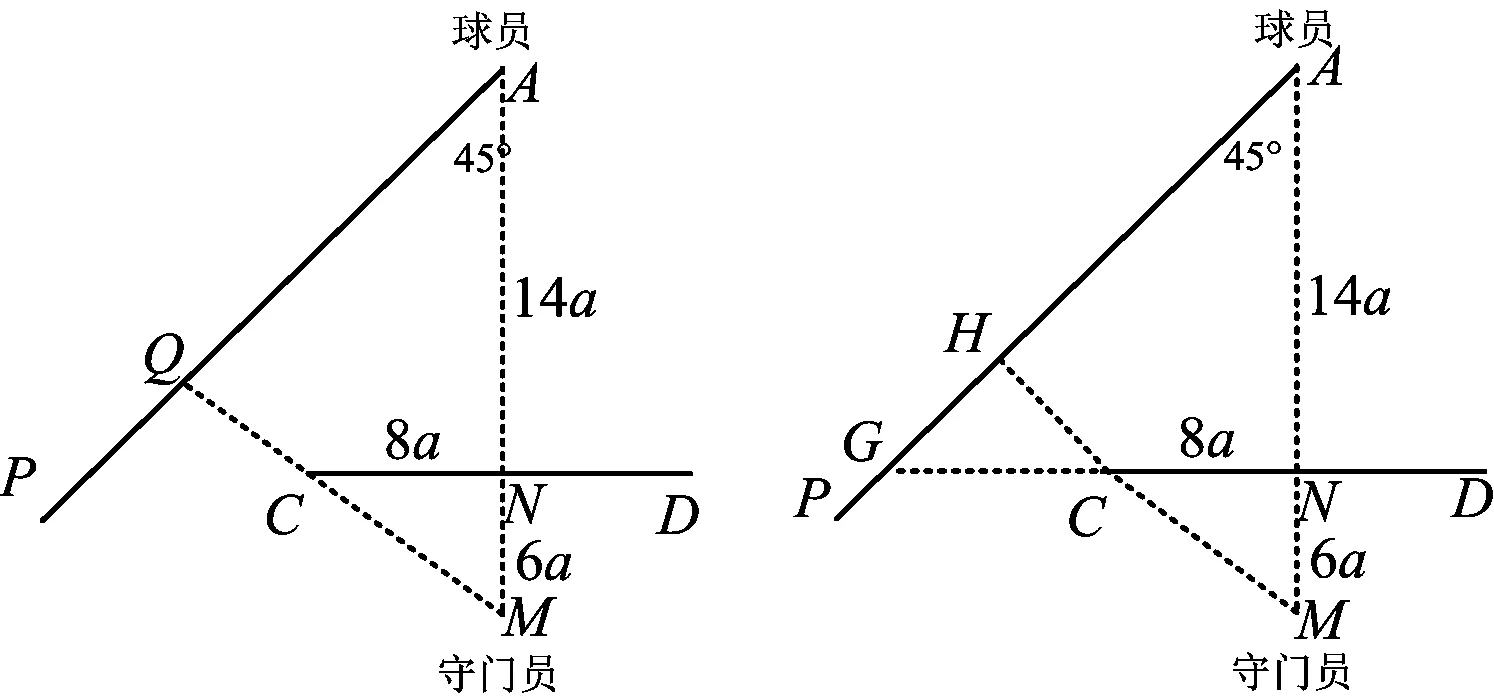
图10 图11
另外根据图形特征,求解CH的思路多元,如图12~14,学生可以联系自己熟悉的知识方法来求解.
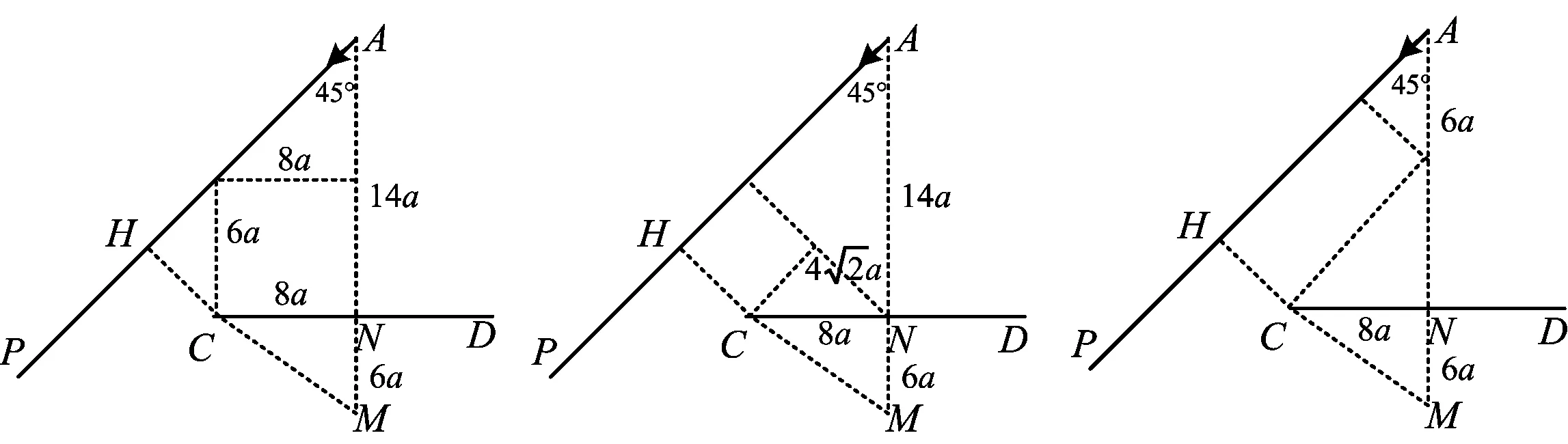
图12 图13 图14
但是此方案人为编写痕迹过大,知识的应用在两个直角三角形中,都是应用勾股定理通过计算解决,知识联系还是比较单一.
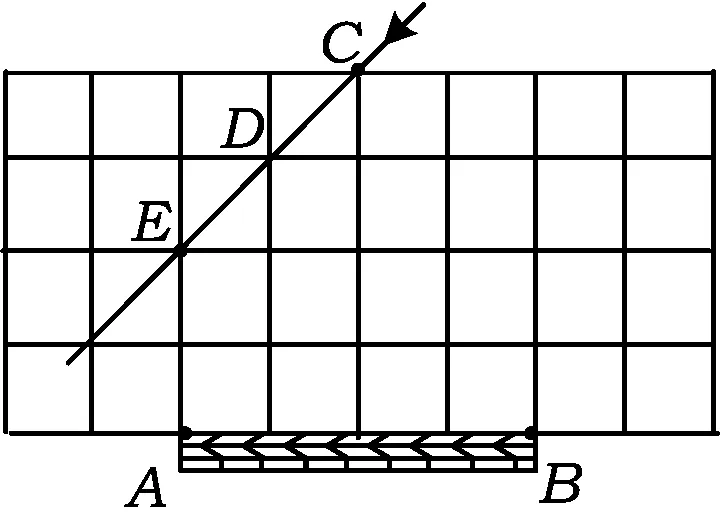
图15
方案6足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小,张角越大,射门越好.如图15的正方形网格中,点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在
( )
A.点CB.点D
C.点ED.线段DE的中点
分析点到球门AB的张角,自然联系以AB为弦的圆,这个圆的圆心在AB的中垂线CM上,这就引导学生去尝试画圆.
作过点A,B,C的圆,如图16,格点F即为AC的中点,联结FG与CM交点O1即为圆心,这时发现点D,E都在该圆的内部,即∠ACB最小;作过点A,B,E的圆时,AE的中垂线与CM交点O2即为圆心,作出⊙O2时,发现点D也在该圆上(如图17).若设小正方形边长为a,则

这也说明了点A,B,D,E共圆,于是∠ADB=∠AEB,这时DE的中点在⊙O2内.故选D.
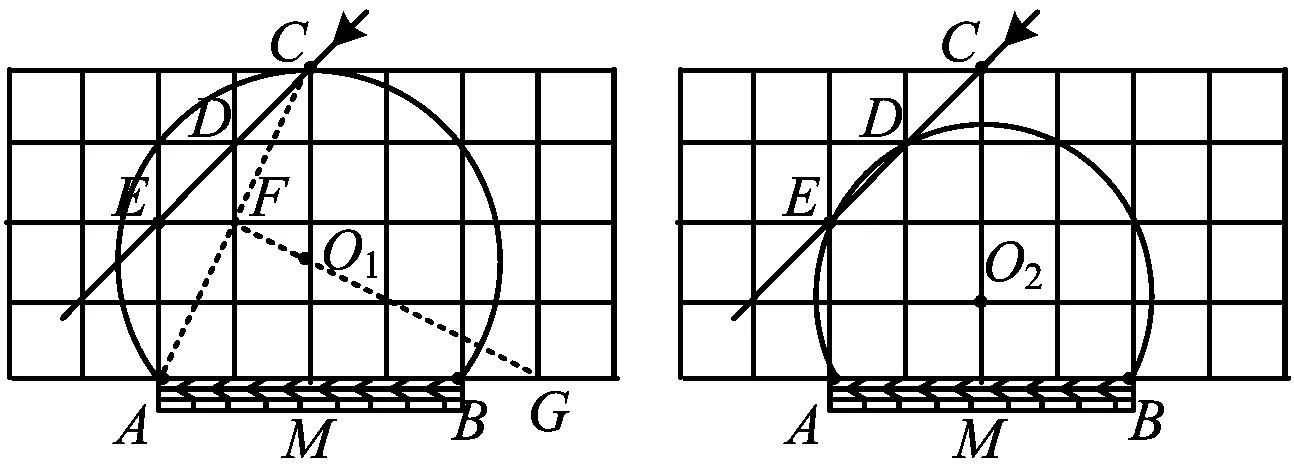
图16 图17
但是,该方案在选项的设置上,点D与点E在同一圆上,选项B,C迷惑不强,难以甄别学生对相关数学知识的清晰认识.另外,最好的射点是否在DE的中点还有待探究.为此,将选项适当修改,形成方案7.
方案7(定稿) 足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小,张角越大,射门越好.在如图15所示的正方形网格中,点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在
( )
A.点CB.点D或点E
C.线段DE(异于端点)上一点
D.线段CD(异于端点)上一点
分析定稿后的试题,以足球射门最好的射点位置探究为背景,要求学生结合文字信息,在其示意图中,通过“联系知识、画图操作、探究猜测”来确定最好的射点,为学生提供了探究、发现、思考的空间,较好地考查了学生对圆知识的理解、掌握和灵活运用的程度,以及学生的空间观念、空间想象与活动经验,加强了对数形结合思想与合情推理能力的重视.
背景用网格,避免了学生作图过程中的繁琐过程,充分利用图形内在的位置关系、数量关系来考查学生对数学本质的理解层次.
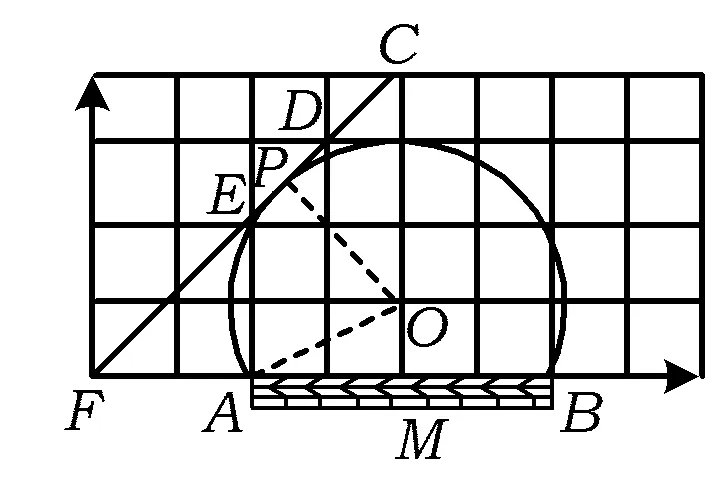
图18
进一步思考:最大射角的点是否在线段DE的中点处?如图18,设过点A,B的⊙O与EC相切于点P,设小正方形边长为a,⊙O半径为x,则

在Rt△AOM中,
AM2+OM2=OA2,
即

化简得


此时

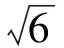
3 命题反思
该试题的编制过程采用“选择生活情景,联系数学知识,抽象数学模型,探究考查方向”的方法,通过不断尝试,形成试题.这给编制含有拓展性课程设计理念的数学试题带来很多启发.
1)选择实际情景.为了考查学生运用数学知识解决实际问题的能力,选择一个真实的、蕴含数学知识的实际生活情景,通过建模,抽象出数学问题,来实现现实问题数学化.足球场地,学生极为熟悉,其中蕴含的数学知识极为丰富,是拓展性课程常选的素材.从游戏、最值问题到最佳射点的探究,这需要激活学生原有的知识和能力以及数学学习经验,运用到该情景之中,有一定的现实意义,关注了空间图形与生活的结合,体现数学的实用价值.
2)设置考查问题.试题的问题设置:1)设问方向联系实际需求,当运球路线所在直线与球门AB有交点时,研究张角大小;当运球路线所在直线与球门AB无交点时,一方面探究守门员到运球路线的最近路程,另一方面是带球队员进攻时射点的选择,接近于生活实际.2)问题呈现体现研究过程,如定稿后的试题,联系到有关圆的知识后,作过点A,B的圆时,需要几何直觉,根据正方形网格隐含的几何条件,作⊙O1得出∠ACB最小,利用三角形相似作中垂线后进一步作出⊙O2,并通过计算验证得4个点A,B,D,E共圆,得出∠ADB=∠AEB,线段DE(异于端点)在⊙O2内,容易得出答案.让学生经历以“操作、发现、猜想和验证”为活动主线的问题探究过程,在问题的解决过程中,包含对模型的分析和对方法的思考.
3)体现教学导向.抽象出的几何图形是学生熟悉的,联系知识后画图探究离不开学生平时的数学活动经验积累,将圆、正方形、直角三角形等核心知识,通过图形变化联系在一起,借助转化、猜想、计算等形式,较好地实现了知识的整合,突出考查学生应用所学知识解决问题的思维过程,体现良好的教学导向,学习数学关注切实的体验、实践以及数学活动经验的积累,重视读图、认图、释图能力的培养.
2017-06-30
傅瑞琦(1966-),男,浙江金华人,中学高级教师.研究方向:数学教育.
O123. 1
A
1003 - 6407(2017)11-24-04

