单轴旋转捷联惯导系统尺寸参数辨识与转位设计

郭琦，周召发，孙立江，徐梓皓，陈河

火箭军工程大学 定位定向与光电瞄准实验室，西安 710025

单轴旋转捷联惯导系统尺寸参数辨识与转位设计

郭琦*，周召发，孙立江，徐梓皓，陈河

火箭军工程大学 定位定向与光电瞄准实验室，西安 710025

为了求解单轴旋转捷联惯导系统的尺寸参数，推导了参数辨识的公式，并设计了转位方案。首先，分析了单轴旋转捷联惯导系统(SINS)尺寸效应的原理，推导了以加速度计输出量为观测量的尺寸参数辨识方法。然后，针对辨识公式中的载体姿态进行了研究，发现合理的整周旋转方案可以消除载体姿态及姿态误差角对尺寸参数辨识的影响，并基于转位角速度的匀加减速模型，分析了该模型与速度增量误差之间的的关系，设计了转位方案。最后，进行了参数辨识试验，得到的尺寸参数标准差<2.3 mm(1σ)，利用均值补偿二位置对准的尺寸效应后，初始对准精度由69.5″(3σ)提高到47.2″(3σ)，验证了方法的可行性。

单轴旋转；捷联惯导系统；尺寸效应；载体姿态；角速度模型；初始对准

惯性导航是一种高自主性的导航方式[1]，旋转调制技术是其发展的主要方向之一[2-3]。对于实际的旋转式捷联惯导系统，加速度计的物理尺寸和安装误差使得加速度计测量点与转位中心之间存在位移，在惯性测量单元(Inertial Measurement Unit,IMU)旋转时会产生向心加速度和切向加速度，给加速度计测量值带来误差，即尺寸效应误差[4]。尺寸参数也称内杆臂[5]长度，是对上述误差进行补偿的基础。因此，有必要对尺寸参数的标定技术进行研究。

目前尺寸参数的标定方法主要有两种，卡尔曼滤波法和基于最小二乘法的系统辨识。文献[5]对尺寸效应的原理与补偿算法进行了分析。文献[6]以速度误差为观测量设计了卡尔曼滤波器，并在匀角速度旋转、匀角加速度旋转和正弦角加速度旋转等三种方案下进行了仿真，三类方案均能实现尺寸参数精确标定，且以正弦角加速度标定方案估计精度最高。文献[4]分别以速度误差和加速度误差为观测量进行了尺寸参数辨识，发现以速度误差为观测量求解的尺寸参数会有较大误差。但是文献[4,6]都需要速率转台提供精确的转位角速度和角加速度，硬件要求比较高。文献[7]假设陀螺能够准确测量转位角速度，以速度误差为观测量进行系统辨识。文献[8]根据激光陀螺角增量采样值采用多子样拟合法求解角速度和角加速度。值得注意的是，文献[4,7-8]都以尺寸效应补偿前后纯惯性导航解算的速度误差减小的比例作为衡量尺寸参数标定结果优劣的标准。

已知二位置对准在驻停位置进行滤波，在旋转过程中进行纯惯导解算。理想情况下，尺寸效应补偿后，全程滤波增加了滤波时间，应当可以提高对准精度。笔者在实验中发现，有些尺寸参数虽然可以减小速度误差，但是补偿尺寸效应后全程滤波的精度不如二位置对准。原因在于，初始对准以速度误差作为观测量，尺寸效应补偿后残余的速度误差使得初始对准滤波器不能对系统误差特性进行准确的估计。因此以补偿前后纯惯导解算速度误差的降幅作为尺寸参数标定精度的衡量标准有一定的局限性。

以加速度为观测量推导了尺寸参数辨识的方法，并结合实际单轴旋转捷联惯导系统(SINS)的工作环境，研究了载体姿态和转位角速度模型对尺寸参数辨识的影响，以此为基础设计了转位方案。最后，设计了初始对准试验对尺寸参数精度进行检验。

1 尺寸效应分析与参数辨识

1.1 相关坐标系的定义

地心惯性坐标系i：原点Oi位于地心，xi轴指向春分点，zi轴与地球自转轴重合，方向与自转方向一致，yi轴与xi、zi轴构成右手坐标系。

地球坐标系e，原点Oe位于地心，xe轴指向本初子午线与赤道的交点，ye轴指向东经90°子午线与赤道的交点，ze轴与地球自转轴重合，方向与自转方向一致。e系固联在地球上，以15.041 1(°)/h的角速率绕地轴即绕i系旋转[9]。

地理坐标系g：原点Og位于载体重心，xg和yg水平指向东向和北向，zg轴沿大地垂线方向指向天顶，也称为东北天坐标系。

导航坐标系n：在导航时根据系统的需要而选取的作为导航基准的坐标系[10]。此时，选取地理坐标系为导航坐标系。

载体坐标系b：原点Ob位于载体重心，xb轴沿载体横轴指向右，yb轴沿载体纵轴指向前，zb轴与xb、yb轴构成右手坐标系[11]。

IMU坐标系s：原点Os位于IMU的重心，三轴指向为惯性器件敏感轴方向[12]。

1.2 尺寸效应的原理

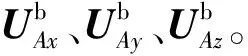
以加速度计Ax为例，载体重心相对于地心的位置矢量为rb,加速度计测量点相对于地心的位置矢量为rs,加速度计测量点相对于载体重心的位置矢量为rx,三者的位置关系如图2所示。

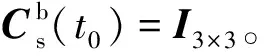
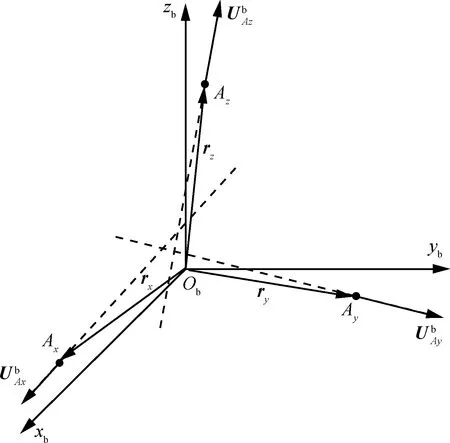
图1 加速度计的安装[13]Fig.1 Installation of accelerometers[13]

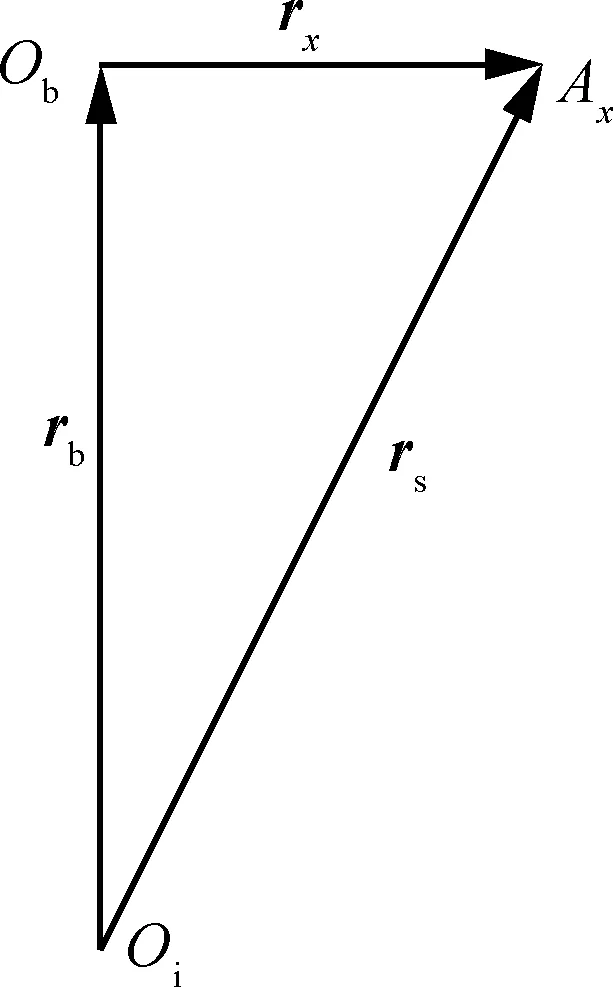
图2 尺寸效应的位置矢量Fig.2 Position vectors of size effect

图3 尺寸效应分析Fig.3 Analysis of size effect

由图2可知

rs=rb+rx

(1)

将式(1)两边对i系求导可得

(2)

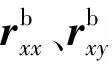
(3)

(4)

根据牛顿第二定律

(5)

式中：fOs为加速度计测量点处的比力；fOb为载体重心处的比力；G为地球重力矢量，模值记为g。将式(5)代入式(4)，并向s系投影，得

(6)

因此，尺寸效应引起的比力测量误差为

(7)

(8)

(9)

将式(9)代入式(7)得

(10)

由于只有敏感轴方向的加速度才能在加速度计输出中体现，且加速度计输出信号为速度增量，因此尺寸效应引起的Ax的有害速度增量为

(11)

式中：ΔT为采样周期。同理，尺寸效应引起的Ay的有害速度增量为

(12)

1.3 以加速度为观测量的尺寸参数辨识

(13)

(14)

取不同时刻t1,t2

(15)

若系数矩阵满秩，即存在逆矩阵，则

(16)

根据比力方程，加速度计有害速度增量为

(2ωie+ωen)×Ven·ΔT+G·ΔT)

(17)

式中：G=[0 0 -g]T；地速Ven=[0 0 0]T；ΔVf是加速度计输出的速度增量；ΔVn是导航坐标系中的地速增量。将G、Ven、ΔVf代入式(17)得

(18)

再将式(18)得到的ΔVs代入式(16)，即可求解出尺寸参数。

2 转位方案设计

2.1 载体姿态对尺寸参数辨识的影响

(19)

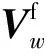
(20)

式中：φn为失准角向量，φn=[φEφNφU]T;

将式(20)代入式(16)得载体姿态误差引起的尺寸参数辨识误差为

(21)

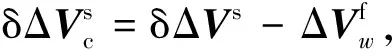
那么，

(22)

由式(22)可知，对于水平加速度计Ax、Ay，载体姿态引起的尺寸参数辨识误差与载体水平姿态角误差φE、φN和转位角度α有关。

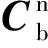
2.2 转位角速度模型对尺寸参数辨识的影响

根据式(16)和式(21)，若要对尺寸参数进行精确辨识，IMU必须存在转位过程；若要对其中的切向分量rxy、ryx进行辨识，还需要存在加减速过程，因此有必要建立相应的转位角速度模型进行定量分析。另根据式(22)可知，研究转位角速度模型对于设计合理的转位方案具有重要意义。

以整周旋转为例。建立如图4所示的匀加减速模型。该模型分为三部分：匀加速阶段、匀速阶段和匀减速阶段，匀加速与匀减速阶段的加速度绝对值相同。

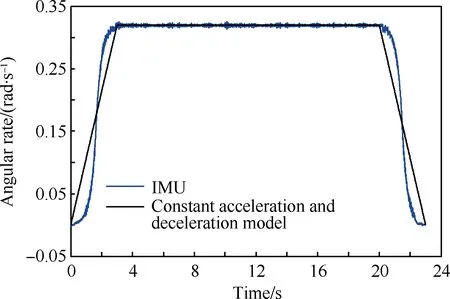
图4 转位角速度的匀加减速模型Fig.4 Constant acceleration and deceleration model of rotational angular rate

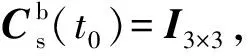
(23)

(24)

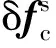
(25)

将式(25)中cosα和sinα按转位阶段拆分求解

加速阶段：

(26)

(27)

式(26)和式(27)无法求出解析解。

匀速阶段：

(28)

令u=t-t1/2

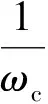
(29)

同理，

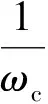
(30)

又ωct2+ωct1/2=2π-ωct3/2=2π-ωct1/2，故

(31)

(32)

减速阶段：

(33)

令u=t1+t2+t3-t且t3=t1

(34)

同理

(35)

对式(26)、式(27)、式(31)、式(32)、式(34)、式(35)求和得

(36)

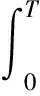
(37)

代入式(25)得整周旋转累积的s系速度误差为

(38)

以图5中的b点和g点为例，分析加减速阶段满足轴对称条件任意两点的角速度关系。b点和g点的角速度关系如图6所示。

图6 加减速阶段任意轴对称两点的角速度关系 Fig.6 Angular relationship between arbitrarily two points at acceleration and deceleration axisymmetric positions

图6中曲线反映了真实单轴旋转捷联惯导系统转位一周计算出的角速度与时间之间的关系，梯形折线是转位角速度的匀加减速模型。b′是b的映射点，其中b点表示IMU的真实角位置，b′点表示根据模型推算的角位置，二者角速度相同。根据积分原理可知，斜线阴影部分的面积反映了相应的时间区间内角速度的积分，也就是角度α。

下面结合图5和图6从轴对称和中心对称两个方面对式(36)、式(37)、式(38)进行分析。以式(38)中的第一个分量为例，

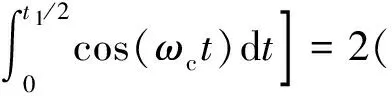
(39)

综上所述，要消除载体姿态和转位角速度模型引起的辨识误差，须采用整周旋转方案并保证轴对称和中心对称任意两点的角速度相等。该结论为设计转位方案提供了依据。

2.3 转位方案

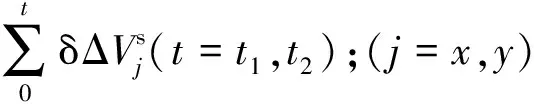
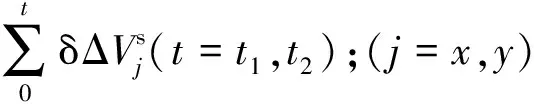
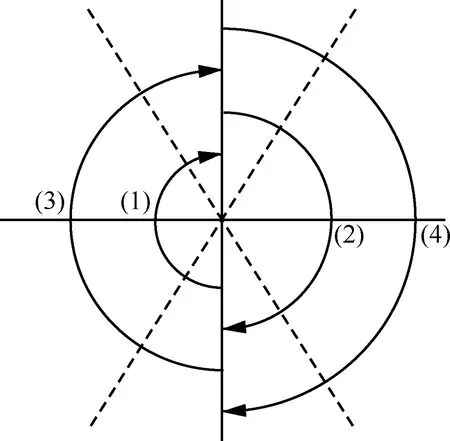
图7 转位方案设计Fig.7 Designed rotation project

3 试验验证与分析

主要仪器为某型单轴旋转捷联惯导系统、双轴位置转台、基准棱镜和高精度经纬仪。激光陀螺常值漂移为0.005 (°)/h，加速度计零偏为3×10-5g，g=9.794 06 m/s2。

已知角速度的微分为角加速度，即

(40)

角增量等于角速度在一个采样间隔内的积分，即

Δθ=ω·ΔT

(41)

(42)

(43)

对式(42)和式(43)进行可观测性分析。可观测性矩阵为

(44)

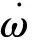
对比可知，卡尔曼滤波可以有效降低滤波值中的噪声。重复图7所示整周旋转10次，尺寸参数辨识结果如表1所示。

二位置对准一般在位置一和位置二进行滤波，在转位过程进行纯惯导解算。在不延长整体初始对准时间的情况下，如果可以将转位过程的有效信息纳入滤波环节，实质上等效于增加滤波信息量，延长滤波时间，有助于提高初始对准精度。转位过程不能直接用于精对准滤波的主要原因是加速度计尺寸效应在转位过程中会产生切向和法向加速度，使得加速度计输出值中叠加了相应的误差。若要实现全程精对准滤波，须求解加速度计尺寸参数并进行补偿。

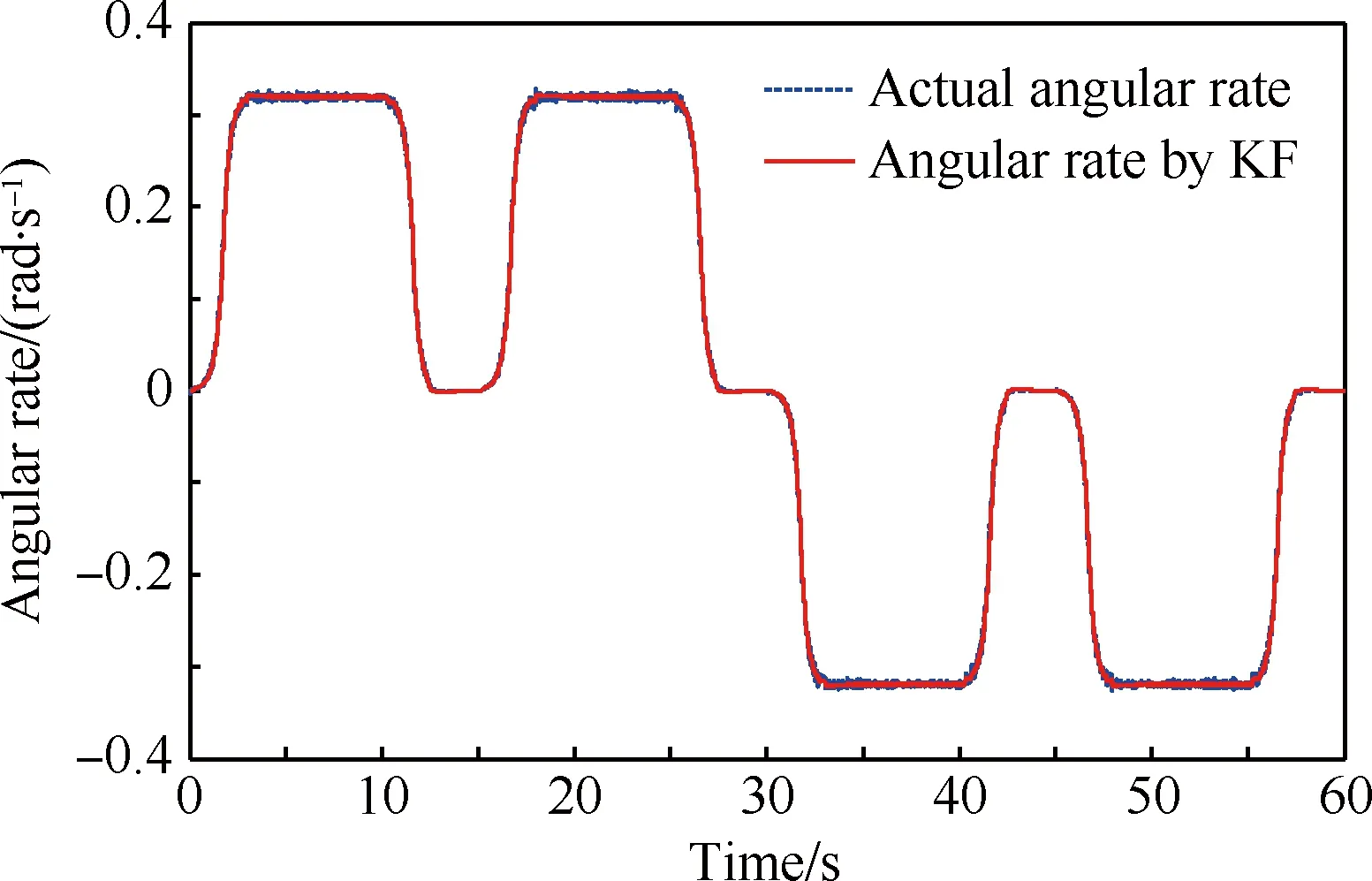
图8 转位角速度卡尔曼滤波结果Fig.8 Rotational angular rate by Kalman filter

图9 转位角加速度卡尔曼滤波结果Fig.9 Rotational angular accleration rate by Kalman filter

表1 尺寸参数辨识结果Table 1 Calculated size effect parameters mm

利用尺寸参数均值补偿对径正反转停二位置对准转动过程的加速度计输出，补偿前后的速度误差如图10和图11所示，Ve、Vn、Vu分别表示东向、北向、天向速度。

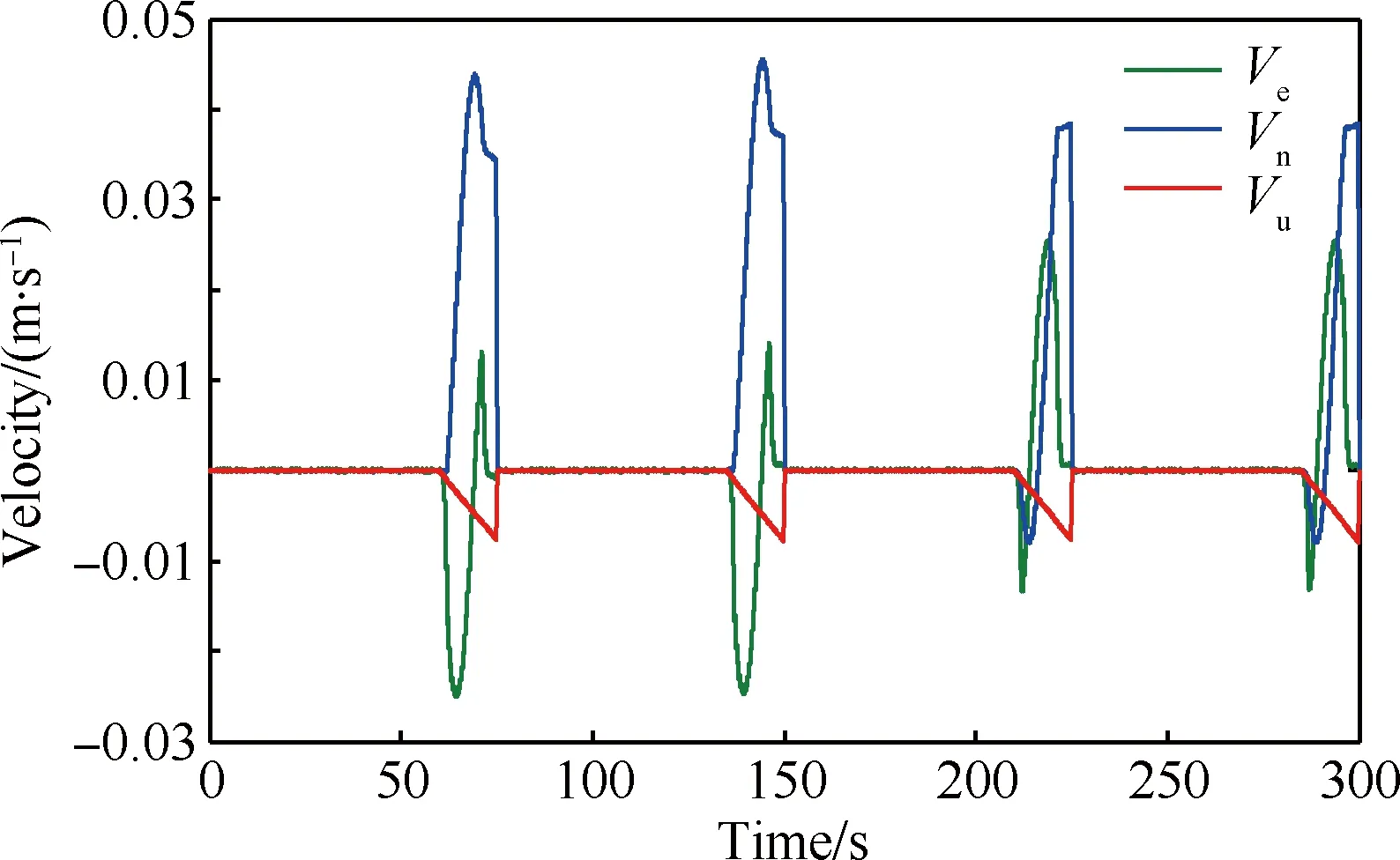
图10 二位置对准的速度误差Fig.10 Velocity errors of two-position alignment

图11 补偿尺寸效应后二位置对准的速度误差Fig.11 Velocity errors of two-position alignment after size effect compensation

如图10和图11所示，补偿尺寸效应后，转动过程中滤波后的东向速度误差减小约52%，北向速度误差减小约69%。

以补偿尺寸效应后的速度误差为观测量，在300 s全程进行卡尔曼滤波初始对准，以检验尺寸参数的精度。滤波后的速度误差如图12所示，补偿前后的对准航向角如表2所示,真值由基准棱镜和高精度经纬仪得到。

图12 补偿尺寸效应后300 s全程对准的速度误差Fig.12 Velocity errors of 300 s alignment after size effect compensation

由表2可知，补偿尺寸效应后对准航向角相对于真值的三倍标准差由69.5″提高到47.2″。

表2 补偿尺寸效应前后的对准结果对比

4 结 论

1) 以加速度为观测量推导了单轴旋转捷联惯导系统尺寸参数辨识的方法。

2) 研究了载体姿态和转位角速度模型对尺寸参数辨识的影响，并得出结论：采用整周旋转方案且中心对称的两个点的角速度绝对值相等时，载体姿态和转位角速度模型的影响可以分别抵消。

3) 设计了加速度计尺寸参数辨识的对径正反旋转方案。

4) 进行了初始对准试验并得出结论：补偿尺寸效应后，对准航向角相对于真值的三倍标准差由69.5″提高到47.2″，验证了方法可行性。

[1] 牛小骥, 班亚龙, 张提升, 等. GNSS/INS深组合技术研究进展与展望[J]. 航空学报， 2016, 37(10): 2895-2908.

NIU X J, BAN Y L, ZHANG T S, et al. Research progress and prospects of GNSS/INS deep integration[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(10): 2895-2908 (in Chinese).

[2] HAYS K M, SCHMIDT R G, WILSON W A, et al. A submarine navigator for the 21th century[C]∥Proceedings of IEEE Position Location and Navigation Symposium. Piscataway, NJ: IEEE Press, 2002: 179-188.

[3] ISHIBASHI S, TSUKIOKA S, SAWA T, et al. The rotation control system to improve the accuracy of an inertial navigation system installed in an autonomous underwater vehicle[C]∥Proceedings of Symposium on Underwater Technology and Workshop on Scientific Use of Submarine Cables and Related Technologies, 2007: 495-498.

[4] 任磊, 杜建邦, 王美娥. 旋转惯导中加速度计尺寸效应误差分析及补偿[J]. 航空学报, 2013, 34(6): 1424-1435.

REN L, DU J B, WANG M E. Error analysis and compensation of size effect in INS with IMU rotation[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(6): 1424-1435 (in Chinese).

[5] 严恭敏, 严卫生, 徐德民. 捷联惯性测量组件中内杆臂效应分析与补偿[J]. 中国惯性技术学报, 2008, 16(2): 148-153.

YAN G M, YAN W S, XU D M. Analysis and compensation on inner lever arm effect of strapdown inertial measurement unit[J]. Journal of Chinese Inertial Technology, 2008, 16(2): 148-153 (in Chinese).

[6] 游金川, 秦永元, 杨鹏翔, 等. 捷联惯导加速度计尺寸效应误差建模及其标定[J]. 宇航学报, 2012, 33(3): 311-317.

YOU J C, QIN Y Y, YANG P X, et al. Modeling and calibration of the accelerometer size effect error of the SINS[J]. Journal of Astronautics, 2012, 33(3): 311-317 (in Chinese).

[7] 江奇渊, 汤建勋, 袁保伦, 等. 激光陀螺捷联惯导尺寸效应误差分析与补偿[J]. 红外与激光工程, 2015, 44(4): 1110-1114.

JIANG Q Y, TANG J X, YUAN B L, et al. Analysis and compensation for size effect error of laser gyro strapdown inertial navigation system[J]. Infrared and Laser Engineering, 2015, 44(4): 1110-1114 (in Chinese).

[8] 吴文启, 杨伟光, 杨杰. 激光陀螺捷联惯导系统尺寸效应参数标定与优化补偿[J]. 中国惯性技术学报, 2009, 17(6): 636-642.

WU W Q, YANG W G, YANG J. Calibration and optimal compensation for size effect parameters of laser gyro SINS[J]. Journal of Chinese Inertial Technology, 2009, 17(6): 636-642 (in Chinese).

[9] 秦永元. 惯性导航[M].2版. 北京: 科学出版社， 2014: 3-7.

QIN Y Y. Inertial navigation[M].2nd ed.Beijing: Science Press, 2014: 3-7 (in Chinese).

[10] 高伟, 奔粤阳, 李倩. 捷联惯导系统初始对准技术[M]. 北京: 国防工业出版社, 2014: 2-3.

GAO W, BEN Y Y, LI Q. Initial alignment for strapdown inertial navigation system[M]. Beijing: National Defense Industry Press, 2014: 2-3 (in Chinese).

[11] 严恭敏. 车载自主定位定向系统研究[D]. 西安: 西北工业大学, 2006: 13-14.

YAN G M. Study of vehicle autonomous position and azimuth determining system[D]. Xi’an: Northwestern Polytechnical University, 2006: 13-14 (in Chinese).

[12] 孙伟. 旋转调制型捷联惯性导航系统[M]. 北京: 测绘出版社, 2014: 4-5.

SUN W. Rotary modulation strapdown inertial navigation system[M]. Beijing: Surveying and Mapping Press, 2014: 4-5 (in Chinese).

[13] 谢波, 秦永元, 万彦辉, 等. 捷联惯导系统尺寸效应分析与补偿[J]. 中国惯性技术学报, 2012, 20(4): 414-420.

XIE B, QIN Y Y, WAN Y H, et al. Analysis and compensation for size effect of strapdown inertial navigation system[J]. Journal of Chinese Inertial Technology, 2012, 20(4): 414-420 (in Chinese).

[14] 郭泽， 缪玲娟， 赵洪松. 一种改进的强跟踪UKF算法及其在SINS大方位失准角初始对准中的应用[J]. 航空学报, 2014, 35(1): 203-214.

GUO Z, MIAO L J, ZHAO H S. An improved strong tracking UKF algorithm and its application in SINS initial alignment under large azimuth misalignment angles[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(1): 203-214 (in Chinese).

Sizeparametersidentificationandrotationprojectdesignforsingle-axisrotarySINS

GUOQi*,ZHOUZhaofa,SUNLijiang,XUZihao,CHENHe

LaboratoryofPositioning,OrientationandElectro-opticalCollimation,TheRocketForceUniversityofEngineering,Xi’an710025,China

Tocalculatesizeeffectparametersofsingle-axisrotaryStrapdownInertialNavigationSystem(SINS),relevantexpressionisderivedandrotationprojectisdesigned.Theprincipleofsizeeffectforthesystemisanalyzed,andthemethodutilizingaccelerationmeasurementasobservablesforcalculatingthesizeeffectparametersisproposed.Thebodyattitudeintheexpressionforsizeeffectparametersisanalyzed.Itisconcludedthatreasonablecirclerotationprojectcaneliminatecalculationerrorscausedbybodyattitudeanditserror.Therelationshipbetweenconstantaccelerationanddecelerationmodelofrotationalangularratewithcalculationerrorsisanalyzed.Arotationprojectisthendesigned.Experimentisconductedtoobtainthesizeeffectparameterswithstandarderrors<2.3mm(1σ).Themeanparametersarethenusedtocompensatethesizeeffectoftwo-positionalignment.Precisionofthealignmentisimprovedfrom69.5″(3σ)to47.2″(3σ),demonstratingthefeasibilityofthemethod.

single-axialrotation;StrapdownInertialNavigationSystem(SINS);sizeeffect;bodyattitude;angularratemodel;initialalignment

2016-10-11；Revised2016-11-01；Accepted2016-12-07;Publishedonline2016-12-121416

URL：http://hkxb.buaa.edu.cn/CN/html/20171017.html

NationalNaturalScienceFoundationofChina(41174162)

.E-mailguoqi_academic@163.com

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.320841

V249.322

A

1000-6893(2017)10-320841-11

2016-10-11；退修日期2016-11-01；录用日期2016-12-07；< class="emphasis_bold">网络出版时间

时间：2016-12-121416

http://hkxb.buaa.edu.cn/CN/html/20171017.html

国家自然科学基金(41174162)

.E-mailguoqi_academic@163.com

郭琦，周召发，孙立江，等.单轴旋转捷联惯导系统尺寸参数辨识与转位设计J．航空学报,2017,38(10):320841.GUOQ,ZHOUZF,SUNLJ,etal.Sizeparametersidentificationandrotationprojectdesignforsingle-axisrotarySINSJ.ActaAeronauticaetAstronauticaSinica,2017,38(10):320841.

(责任编辑：张玉， 李世秋)