结冰风洞中液滴过冷特性数值研究

郭向东，王梓旭，李明，肖春华

1.中国空气动力研究与发展中心 空气动力学国家重点实验室，绵阳 621000 2.中国空气动力研究与发展中心 飞行器结冰与防除冰重点实验室，绵阳 621000

结冰风洞中液滴过冷特性数值研究

郭向东1,2,*，王梓旭2，李明2，肖春华2

1.中国空气动力研究与发展中心 空气动力学国家重点实验室，绵阳 621000 2.中国空气动力研究与发展中心 飞行器结冰与防除冰重点实验室，绵阳 621000

为明晰结冰风洞中液滴过冷特性，发展了基于欧拉法的气液两相耦合流动计算方法，模拟了结冰风洞中气液两相耦合流动过程。在此基础上，首先开展了参数影响研究，然后考察了典型结冰风洞构型中三维收缩效应对液滴过冷特性的影响，最后评估了该风洞试验段内液滴过冷状态。结果表明：结冰风洞中液滴过冷特性主要受液滴粒径和气流速度影响，增大液滴粒径和气流速度会显著增加两相温度平衡距离；结冰风洞中的液滴传热过程可以分为准一维传热和三维收缩传热两个阶段，三维收缩传热阶段对液滴过冷状态的影响显著强于准一维传热阶段，三维收缩效应对液滴过冷状态起决定性作用；在典型试验工况下，粒径小于40 μm的小粒径液滴在试验段内均达到过冷状态(液滴气流温度差小于2 ℃)，但粒径大于100 μm的大粒径液滴在高风速条件下(试验段气流速度为157 m/s)未达到过冷状态(液滴气流温度差大于5 ℃)。

飞机结冰；结冰风洞；液滴；过冷；数值模拟

当飞机在云层中飞行时，云层中的过冷水滴(即温度低于冰点的液态水滴)会不断撞击飞机表面，并在其表面产生结冰现象，飞机结冰会破坏飞机气动外形，影响飞机气动性能，严重威胁飞机的飞行安全[1-2]。因此，飞机结冰问题是当前空气动力学研究的热点问题之一。飞机结冰问题的主要研究途径有数值模拟、结冰风洞试验和飞行试验3种，其中结冰风洞试验因其具有结冰条件易控、试验成本相对较低、结果可靠等优点，是目前研究飞机结冰问题最主要的手段[3-5]。结冰风洞是一种开展飞机结冰研究的地面试验设备，其利用喷雾系统(由喷雾耙和喷嘴组成)生成液滴来模拟云层中的悬浮液滴，通过制冷系统和高度模拟系统控制气流温度和气压，从而模拟高空的低温低压环境[6]。在结冰风洞试验中，由于气流温度一般低于冰点，为防止喷雾耙中液态水结冰导致的喷嘴堵塞以及喷嘴出口气流膨胀引起的液滴冻结，一般采用加热方式来提高液态水温度，从而避免了喷嘴堵塞和液滴冻结问题的发生[7]。当喷雾系统中液态水温度过高，生成的液滴到达试验段时，尽管液滴温度低于冰点，但仍可能高于试验段气流静温，使液滴未达到过冷状态(在结冰试验中，液滴过冷状态通过衡量液滴与气流间的温度差来评估)，导致结冰冻结系数减小，溢流增加，进而改变积冰生长过程和冰形特征，影响结冰风洞试验结果。因此，液滴过冷状态的全面评估对结冰风洞试验准确模拟结冰过程具有重要意义。

针对结冰风洞液滴过冷问题，国外主要结冰风洞均开展了相关研究和评估[8-12]。例如，美国NASA 格伦中心Miller等[8]采用基于拉格朗日方法开发的AEDC计算程序[9]，初步评估了NASA Glenn IRT 结冰风洞液滴的过冷状态，结果表明，初始液滴温度对液滴过冷状态无显著影响，风速为195 mph(1 mph=0.447 04 m/s)时，粒径为40、99、160 μm的液滴均达到过冷状态，并通过试验验证了计算结果；意大利航空航天研究中心Ragni[10]和Bellucci[11]等采用三圆柱实验方法评估了CIRA结冰风洞高速试验段和低速试验段构型的液滴过冷状态。但是这些研究仍处于工程层面，多为对液滴过冷状态的评估，缺乏对结冰风洞中液滴过冷特性规律性的认识。

近年来，随着国内飞机结冰问题研究的不断深入，尤其是国内大型结冰风洞——3 m×2 m结冰风洞建成后，液滴过冷问题亟待解决。中国空气动力研究与发展中心易贤等[13]率先建立了基于拉格朗日法的液滴运动及传质传热数值模拟方法，初步研究了不可压缩气流中的液滴传热过程，为评估3 m×2 m结冰风洞中液滴过冷状态奠定了基础；南京航空航天大学朱春玲等[14]采用基于拉格朗日法的液滴传质传热数值模拟方法，开展了不可压缩流动中液滴传热过程参数影响研究。

基于以上研究，本文进一步针对结冰风洞中气流可压缩性以及气液耦合作用，发展了基于欧拉法的气液两相耦合流动计算方法，模拟了实际结冰风洞中气液两相耦合流动过程。在此基础上，首先开展了参数影响研究，揭示了影响液滴过冷特性的主要因素，然后针对3 m×2 m结冰风洞，考察了三维收缩效应对液滴过冷特性的影响，最后评估了该风洞试验段内液滴过冷状态，为国内飞机结冰地面模拟试验数据应用评估提供了支撑。

1 计算方法

1.1 控制方程和物理模型

本文将液滴视为连续流体，采用欧拉方法描述气液两相耦合流动过程，为获得简化物理模型，对气液两相进行以下假设[15-17]：① 气相为理想气体，遵循理想气体法则；② 液滴为球形，不发生变形和破碎，液滴间不发生碰撞；③ 液滴体积相对于气相体积可以忽略，液滴内温度均匀分布；④ 忽略重力效应；⑤ 黏性和热传导效应仅发生在气液两相间；⑥ 不考虑液滴蒸发和冻结过程以及水蒸气凝结过程，认为两相间不存在质量交换。

基于以上假设，简化后的控制方程组为

(1)

(2)

(3)

(4)

(5)

(6)

式中：ρg、p、Vg和Eg分别为气相密度、气相压力、气相速度矢量和气相能量；α、ρd、Vd和hd分别为液滴体积分数、液滴物理密度、液滴速度矢量和液滴显焓；D为液滴阻力，表达式为

D=K(Vg-Vd)

(7)

其中：K为相间动量交换系数，表示为

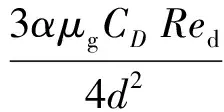
(8)

其中：μg为气相黏性系数；d为液滴直径；Red为液滴相对雷诺数，表示为

(9)

CD为液滴阻力系数，因假设液滴为球形且运动中不发生变形，故采用圆球标准阻力系数[18]，表示为

(10)

Q为热交换率，表示为

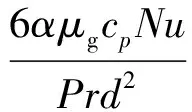
(11)

其中：Tg为气相静温；Td为液滴温度；cp为气相等压比热；Pr为普朗特数，Pr=cpμg/κg,κg为热传导系数；Nu为努塞尔数，采用Ranz-Marshall半经验关系式[19]， 有

(12)

1.2 数值方法

针对可压缩流动过程，采用有限体积方法对两相控制方程进行离散，时间离散采用二阶Euler格式，空间离散采用二阶迎风型的Roe格式，源项隐式处理[20]。

气液两相边界条件采用不同形式处理，对于气相，入口采用压力入口条件，出口采用压力出口条件，壁面采用无黏滑移壁面条件(假设⑤)；对于液相，入口采用速度入口条件，出口采用出流条件，壁面处认为液滴可以直接穿过，不考虑壁面对液相的作用。

1.3 验证算例

为验证本文计算方法的合理性，选取文献[8]中针对NASA Glenn IRT 结冰风洞中液滴过冷状态数值评估结果，作为本文验证算例，验证结果如表1所示，其中试验段风速为87 m/s，试验段静温为-6 ℃，初始相对湿度为83%。从表中可以看出，本文计算的试验段液滴气流温度差结果与文献计算结果的最大差量约为1 ℃，在工程误差范围内。与文献[8]中计算方法相比，本文方法未考虑液滴蒸发等相变传质过程(假设⑥)，因此这可能是本文计算结果与文献[8]结果存在一定偏差的原因，但在实际结冰风洞试验中，为避免液滴蒸发造成的液态水含量损失，试验前会增加风洞内气流相对湿度，进而减弱了液滴蒸发效应，因此针对液滴过冷问题，忽略蒸发传质过程，并不会给计算结果带来显著的误差，这一点从验证结果中也可以看出。综上所述，本文计算方法在一定程度上可以合理模拟结冰风洞中液滴传热过程。

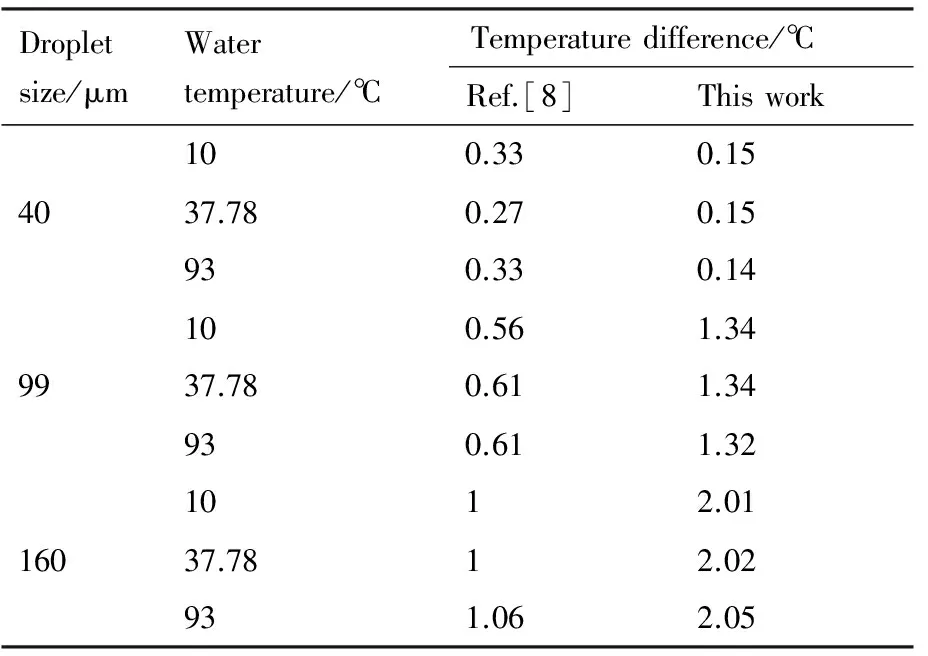
表1 与文献[8]温度差对比

2 结果分析与讨论

以3 m×2 m结冰风洞应用背景为牵引，本节首先开展了参数影响研究，理论分析了各参数对液滴过冷特性的影响规律，然后针对3 m×2 m结冰风洞构型，分析了构型中的液滴传热过程，考察了三维收缩效应对液滴过冷特性的影响，揭示了影响液滴过冷特性的主要因素，最后在典型试验工况范围内，评估了3 m×2 m结冰风洞液滴过冷状态。

2.1 参数影响

液滴传热过程受到许多参数的影响，这些参数可以大致分为液滴参数和气流参数两类，其中液滴参数包括液态水含量LWC、液滴粒径d、液滴初始温度Tdi和液滴初始速度Udi，气流参数包括气流初始静温Tgi和气流速度Ug。为明晰液滴参数和气流参数对液滴过冷特性的影响规律，采用一维定常控制方程组，开展参数影响研究，表2给出了根据结冰风洞典型试验工况设置的基准初始参数。

首先考察液态水含量对液滴过冷特性的影响，根据联邦航空条例FAR 25部附录C和附录O 中典型结冰条件[21]，选取0.5、1.0、2.0和3.0 g/m3这4种液态水含量开展对比研究。图1给出了不同液态水含量下液滴温度变化曲线，从图中可以看出，随着液态水含量的增加，液滴与气流间交换的总能量增多，两相温度平衡后，液滴气流平衡温度增大，但由于液滴质量分数小于1%，因此液滴传热对气流温度和两相温度平衡位置影响有限，图中水含量从0.5 g/m3增至3.0 g/m3，液滴气流平衡温度增加量小于1%并且两相温度平衡位置基本一致(约为0.5 m)，表明液态水含量对液滴过冷特性的影响不显著。

表2 基准初始参数Table 2 Benchmark initial parameters

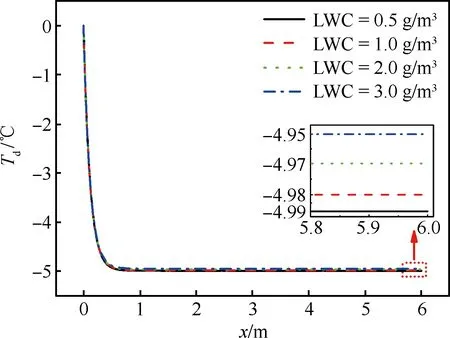
图1 不同液态水含量下液滴温度变化曲线Fig.1 Variation curves of droplet temperature with different liquid water contents

为考察液滴粒径和气流速度对液滴过冷特性的影响，根据FAR 25部附录C和附录O中典型结冰条件[21]，选取20、40 μm的小水滴和100、160、200 μm的大水滴研究液滴粒径的影响，同时考虑到喷雾系统位于风洞稳定段处，气流速度较低，因此选取5、10、20、40和50 m/s这5个风速研究气流速度的影响。

图2给出了不同粒径和气流速度下液滴温度变化曲线，从图中可以看出：液滴温度以指数形式衰减下降，并且随着液滴粒径和气流速度的增加，液滴温度的下降速度减慢，两相温度平衡所经过的距离更长；液滴粒径对液滴温度下降速度和温度平衡距离的影响强于气流速度的影响；具体的，液滴粒径从20 μm增至200 μm，对应的温度平衡距离从约0.2 m增至约14 m，变化十分显著，而气流速度从5 m/s增至50 m/s，对应的温度平衡距离从约0.5 m增至约6 m，变化幅度弱于液滴粒径的影响。进一步，通过理论分析液滴粒径和气流速度的影响规律。首先，在一维定常情况下，液滴能量方程简化为

(13)

式中：Cl为液滴比热；Ud为液滴速率；A定义为温度衰减系数，表征液滴温度衰减的快慢。由于液滴对气流的作用有限，因此假设气流温度和气流速度为常量，同时仅考虑气液速度相同时的等速传热过程，则Nu为常数2。通过以上假设，式(13)的解析解为

(14)

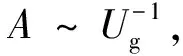
图2 不同粒径和气流速度下液滴温度变化曲线Fig.2 Variation curves of droplet temperature with different diameters and gas velocities

接着考察液滴初始温度和气流初始静温对液滴过冷特性的影响。结冰风洞中，通过调节液滴初始温度，防止喷雾耙中液态水结冰导致的喷嘴堵塞以及喷嘴出口气流膨胀引起的液滴冻结，因此液滴初始温度调节范围被控制在0～100 ℃。此外，根据FAR 25部附录C中的典型结冰条件[21]，气流初始静温分别选取-5、-10、-20、-30 ℃这4个温度。

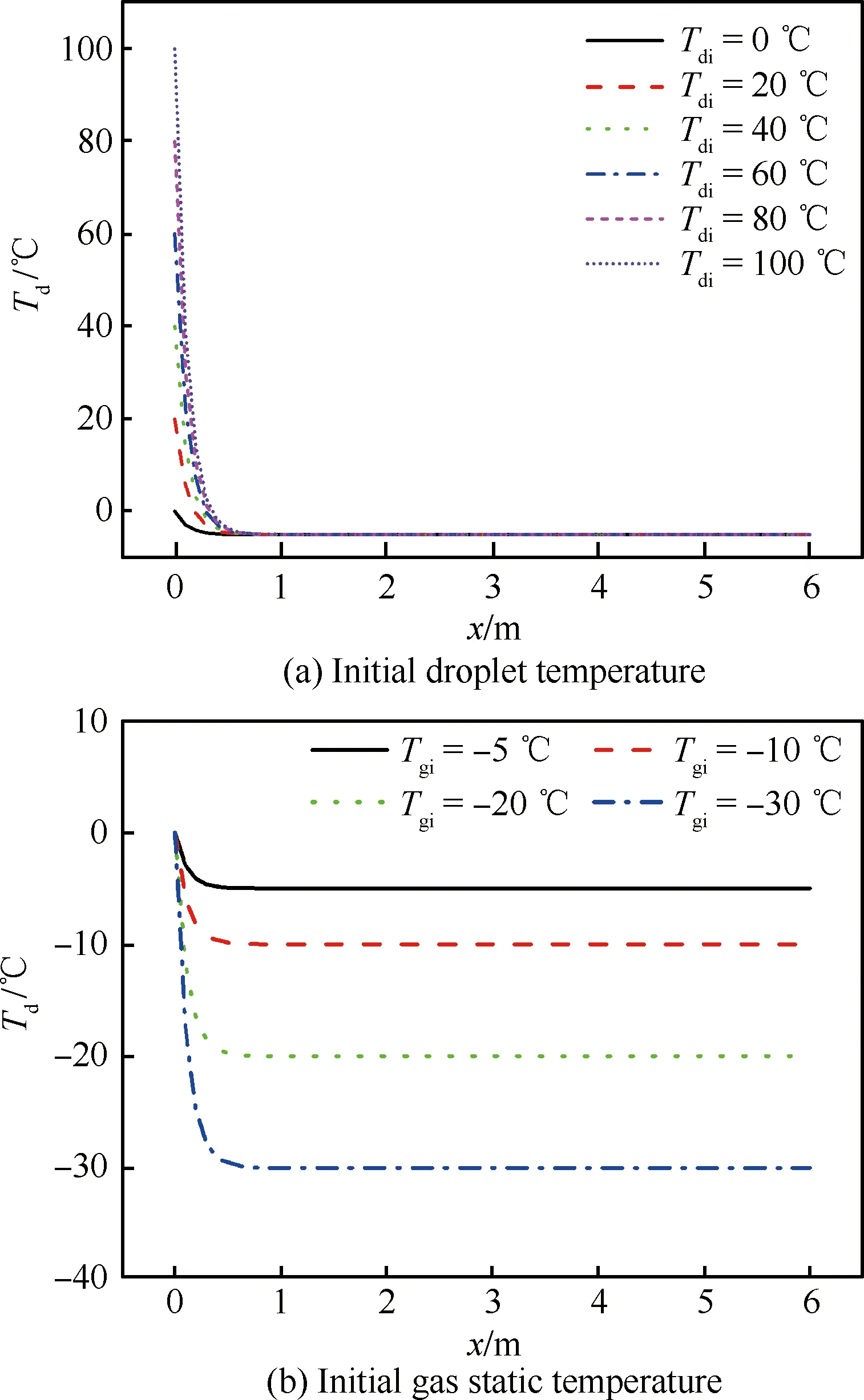
图3 不同液滴初始温度和气流初始静温下液滴温度变化曲线 Fig.3 Variation curves of droplet temperature with different initial droplet temperatures and initial gas static temperatures

图3给出了不同液滴初始温度和气流初始静温下液滴温度变化曲线，从图中可以看出，随着液滴初始温度的增加，液滴温度下降速度增大，与此相反，随着气流初始静温降低，液滴温度下降速度增大，但是两相温度平衡即液滴过冷时，不同的液滴初始温度和气流初始静温对应的平衡距离基本一致，约为0.5 m，表明在典型试验工况下，液滴初始温度和气流初始静温对液滴过冷特性的影响不显著，这与文献[8]中得到的结论一致，进一步验证了本文计算方法的可靠性。从解析解式(14)中，可见液滴初始温度和气流初始静温仅决定气液初始温差，并不影响液滴温度指数减小的趋势，因此在典型试验工况下，液滴初始温度和气流初始静温的显著变化，并不能引起温度平衡位置的显著变化。

最后，考察液滴初始速度对液滴过冷特性的影响。液滴从喷嘴喷出后，其喷出速度受喷雾水压、喷雾气压和喷嘴构型等因素的影响[22]，因此不同试验条件下，液滴初始速度会发生变化，为揭示液滴初始速度的影响规律，选取了5、10、20、40、60 m/s这5个典型速度开展对比研究。由于喷雾耙位于稳定段内，因此液滴初始速度一般高于稳定段风速，液滴喷出后即进入减速传热过程，随着液滴速度降至气流速度，便转换为图2中的等速传热过程。

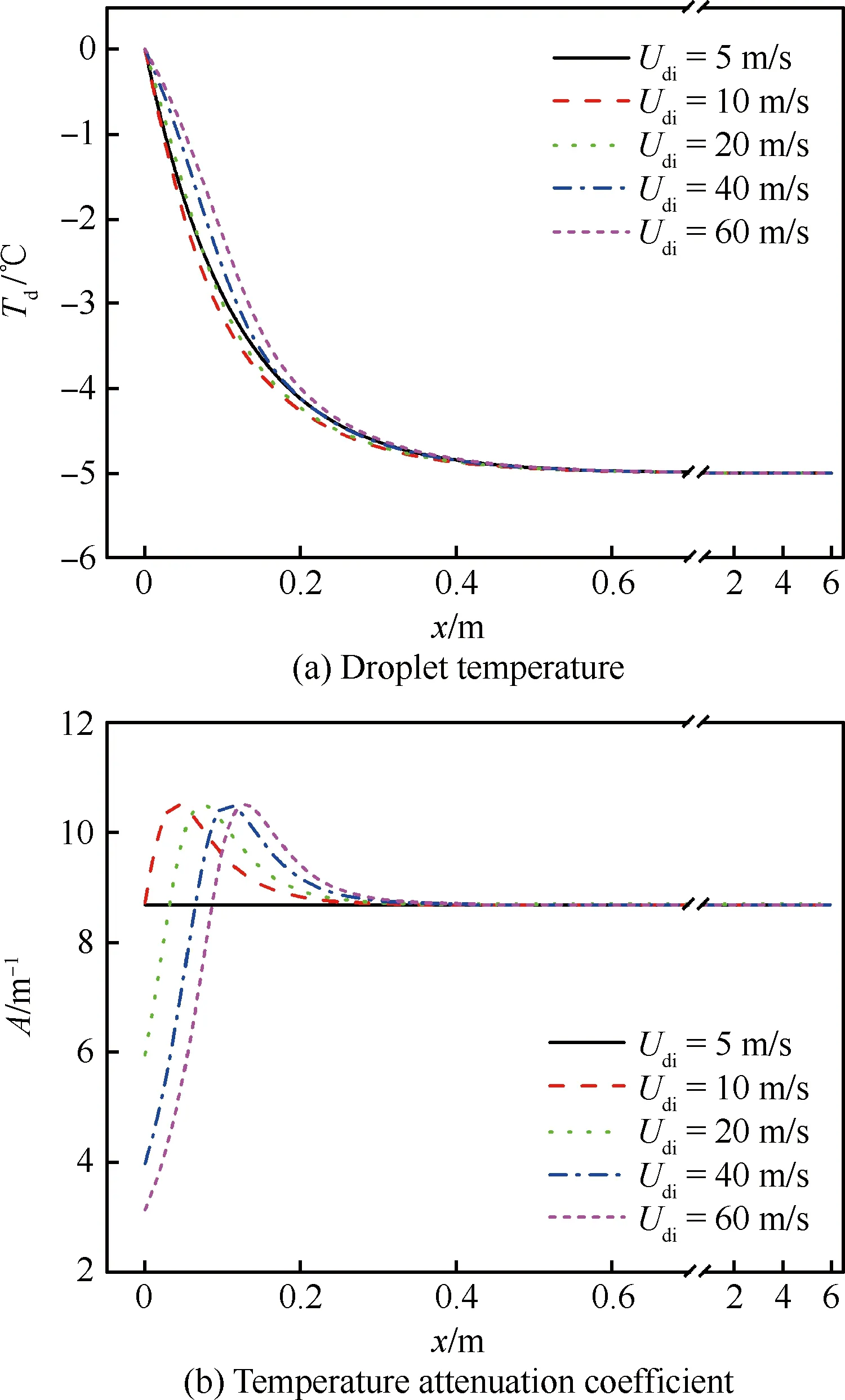
图4 不同液滴初始速度下液滴温度和温度衰减系数的变化曲线 Fig.4 Variation curves of droplet temperature and temperature attenuation coefficient with different initial droplet velocities

图4给出了不同液滴初始速度下液滴温度和衰减系数的变化曲线，从图中可以看出：对比等速传热过程(衰减系数A为常数)，在Nu和液滴速度共同作用下，减速传热过程的衰减系数A形成了先增大后减小的单峰变化趋势，并且随着液滴初始速度的增加，初始衰减系数不断减小，导致单峰影响范围不断增大，液滴温度下降速度先小后大的趋势更加明显；在典型试验工况下，两相温度平衡即液滴过冷时，不同的液滴初始速度对应的平衡距离基本一致(约为0.5 m)，表明液滴初始速度对液滴过冷特性的影响不显著。

2.2 三维收缩效应影响

图5给出了3 m×2 m结冰风洞计算构型，该构型由稳定段、收缩段和试验段3部分组成，构型入口位于稳定段喷雾耙处，出口位于试验段中心处，构型全长16 m，入口截面为高8 m×宽11 m，出口截面为高2 m×宽3 m，收缩比为14.67。

为考察计算构型内液滴传热过程，提取了计算构型中心线处流场参数，开展对比研究。

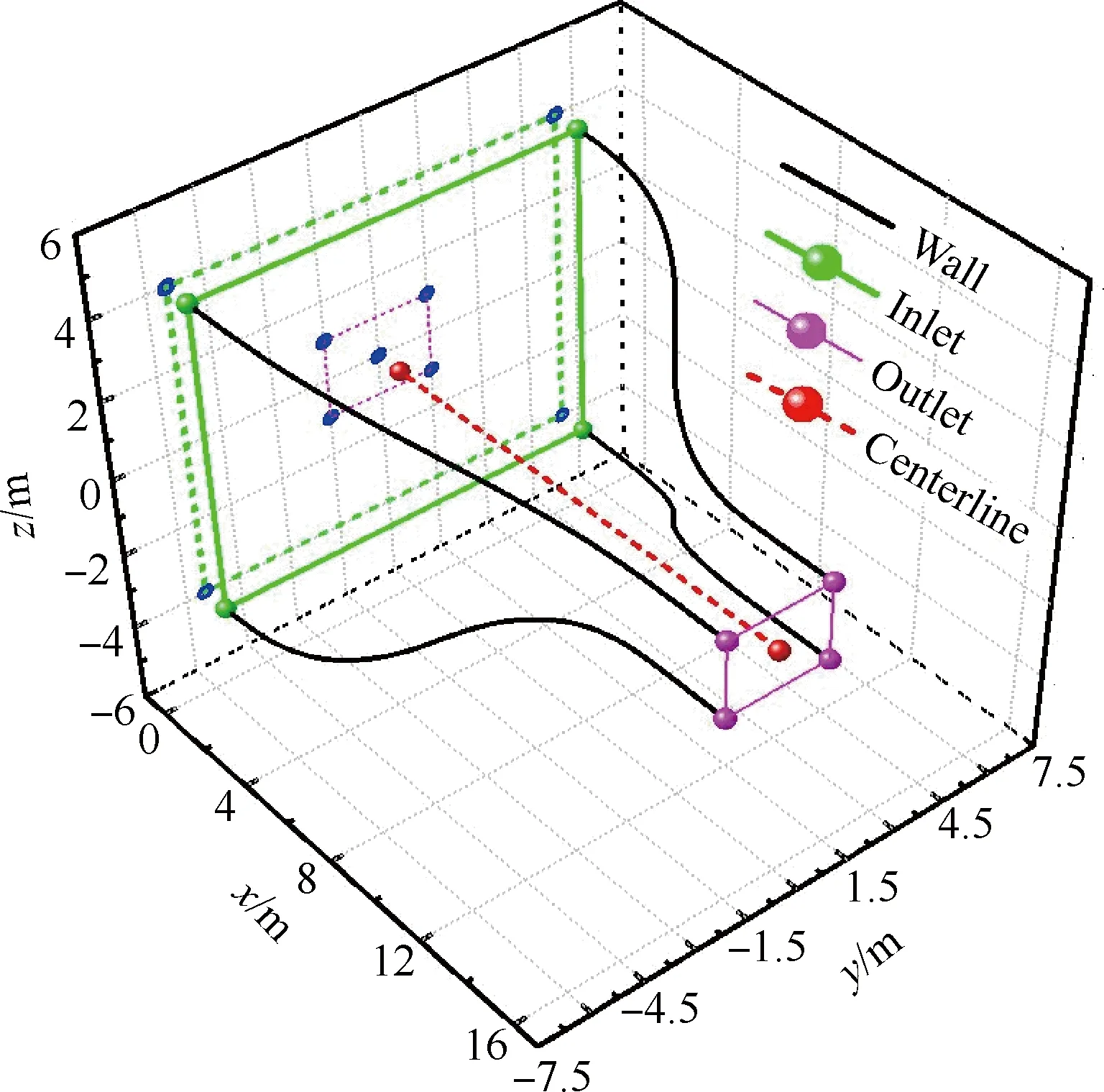
图5 结冰风洞计算构型Fig.5 Icing wind tunnel computational configuration

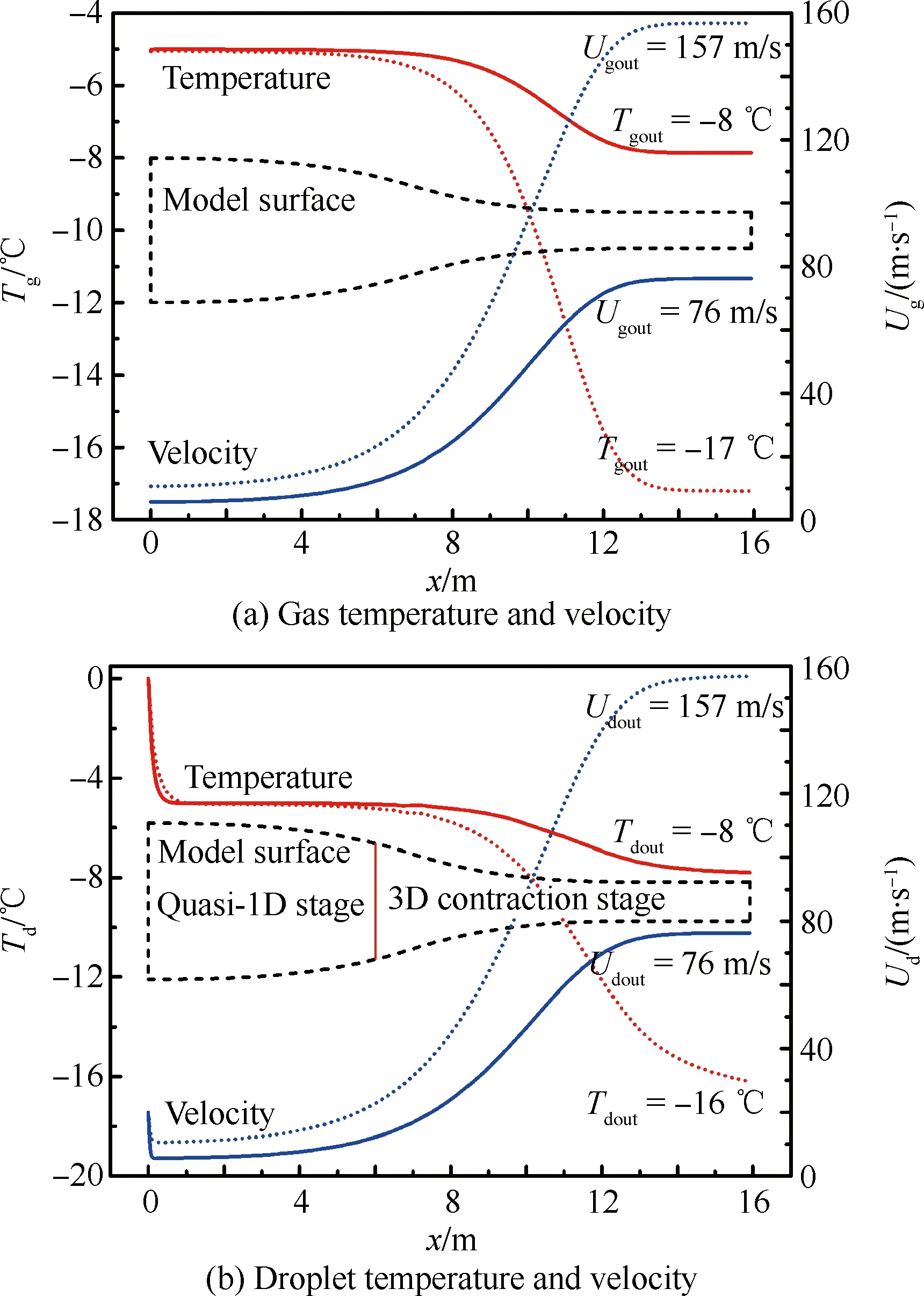
图6 构型中心线处气液温度和速度变化曲线Fig.6 Gas and droplet temperature and velocity profiles along configuration centerline

图6给出了构型中心线处气液温度和速度变化曲线，其中下标out表示构型出口(试验段中心)，计算初始参数为气流总温T0=-5 ℃、Tdi=0 ℃、Udi=20 m/s、LWC=1 g/m3、d=40 μm，图中实线对应试验段风速为76 m/s的工况，点线对应试验段风速为157 m/s的工况。从图中可以看出，整个液滴传热过程近似以构型6 m处截面为界分成两个阶段，此处分别命名为准一维传热阶段和三维收缩传热阶段。准一维传热阶段位于构型入口至6 m处截面之间，此范围内风洞型面变化较缓，三维收缩效应较弱，气流以准一维方式低速流动，气流速度和静温变化较小，接近入口流速和总温；此阶段气流参数稳定，液滴传热过程为准一维稳态传热，液滴首先经历短暂的减速传热，随后液滴速度趋于气流速度，液滴进入等速传热，通过2.1节参数影响分析，可知液滴粒径和气流速度是此阶段液滴过冷特性的主要影响参数，增大液滴粒径和气流速度会显著减慢液滴温度下降速度、增大两相温度平衡距离，而其他参数的影响并不显著。三维收缩传热阶段位于构型6 m处截面至出口之间，此范围内风洞型面变化较大，三维收缩效应较强，气流场发生显著变化，气流速度加速增大，气流静温则等熵下降，出口气流速度越大，出口气流静温越低，如图中所示，气流出口速度76 m/s对应出口静温-8 ℃，而出口速度157 m/s则对应出口静温-17 ℃；此阶段在三维效应的影响下，液滴传热过程从准一维稳态传热过程转变为三维动态传热过程，流场参数间的耦合变化，导致液滴传热过程变得更为复杂。

图7 构型中心线处液气温度差变化曲线 Fig.7 Curves of temperature difference between droplet and gas along configuration centerline

图7给出了构型中心线处液气温度差变化曲线，从图中可以看出：在三维收缩效应的影响下，气流速度沿流向加速增加，气流静温则不断下降，而液滴与气流间存在热迟滞现象，导致气液温差不断增大，在约12 m处(收缩段出口处)，气液温差达到了最大值，随后液滴进入试验段，三维作用结束，流场参数趋于稳定，气液温差不断减小；液滴粒径和出口气流速度(试验段中心气流速度)是三维收缩传热阶段液滴过冷特性的主要影响参数，随着液滴粒径的增大，液滴热惯性不断增强，气液温差不断增大，同时随着出口气流速度的增加，三维效应造成的气流加速更强，气流温度下降更剧烈，导致气液温差不断增大，因此增大液滴粒径和试验段气流速度会增加出口气液温差，导致液滴在试验段处无法达到过冷状态。

为定量评估两个阶段的液滴过冷状态，提取了构型中心线6 m处和出口处的气液温度，开展了对比研究。

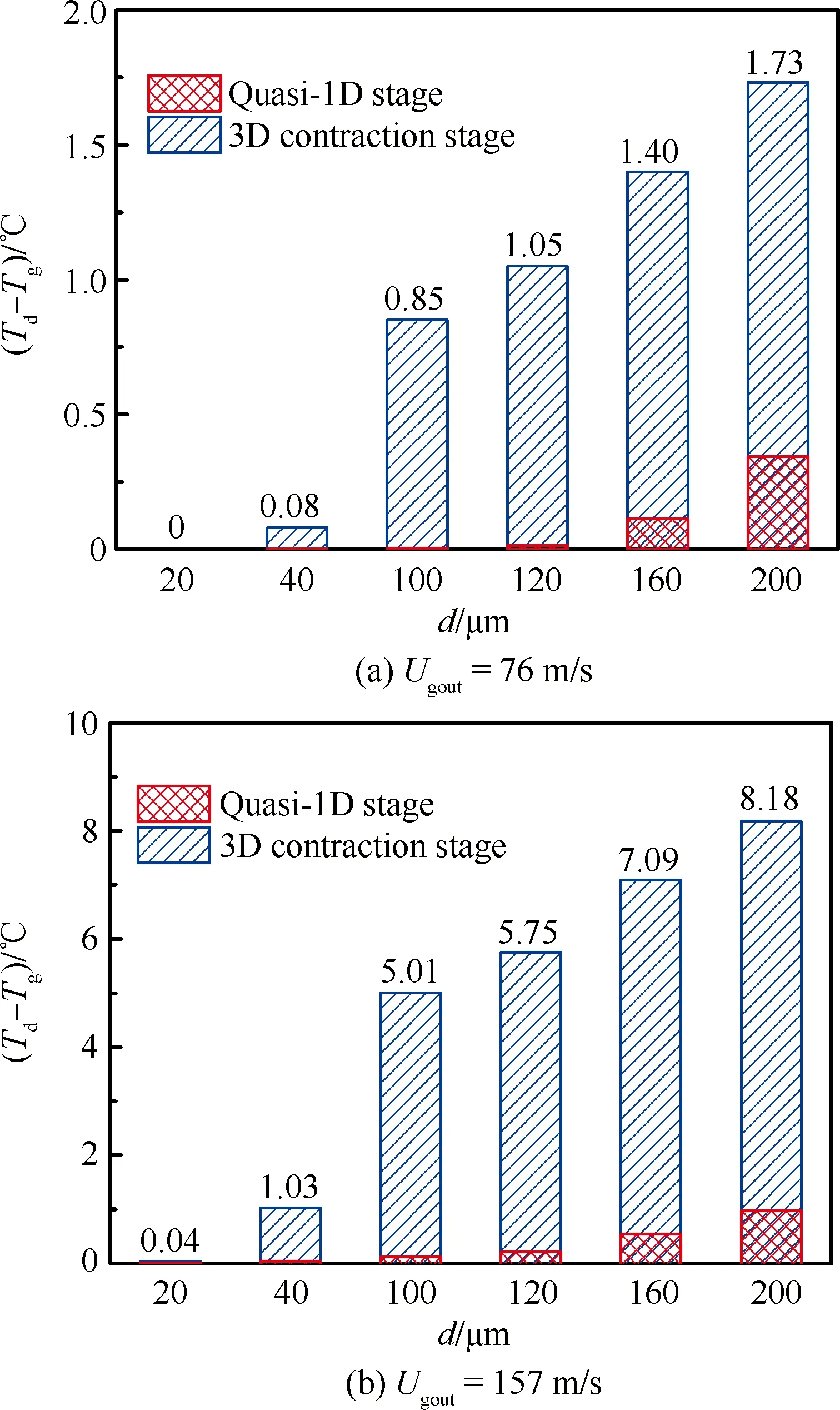
图8 构型出口中心处液气温度差Fig.8 Temperature differences between droplet and gas in center of configuration exit

图8给出了构型出口中心处液气温度差，柱状图中红色部分为构型中心线6 m处液气温度差，表征准一维传热阶段的液滴过冷状态，蓝色部分表征三维收缩传热阶段对液滴过冷状态的影响。从图中可以看出：三维收缩传热阶段对构型出口中心液气温度差的影响显著强于准一维传热阶段；在构型中心线6 m处，粒径200 μm以下的液滴气液温度差均小于1 ℃，表明准一维传热阶段结束时液滴均已达到过冷状态，但由于随后三维收缩效应的影响，导致出口气液温差增大，尤其对于试验段气流速度为157 m/s时，粒径大于100 μm的大粒径液滴已不再过冷，因此可见三维收缩效应对液滴过冷状态起决定性作用；具体的，当试验段气流速度为76 m/s时，粒径小于200 μm的液滴对应的温度差均小于2 ℃，认为粒径小于200 μm的液滴均过冷，当试验段气流速度为157 m/s时，粒径小于40 μm的小液滴对应的温度差小于1.1 ℃，故仍然认为过冷，但粒径大于100 μm的大粒径液滴对应的温度差已超过5 ℃，已不再过冷。

3 结 论

本文发展了基于欧拉法的气液两相流动耦合计算方法，模拟了结冰风洞中气液两相耦合流动过程，研究了结冰风洞中液滴过冷特性。

1) 液滴粒径和气流速度显著影响液滴过冷特性，增大液滴粒径和气流速度会显著减慢液滴温度下降速度、增大两相温度平衡距离，其中液滴粒径影响程度最大为一阶影响量，气流速度较弱为二阶影响量。

2) 结冰风洞中的液滴传热过程可以分为准一维传热和三维收缩传热两个阶段，三维收缩传热阶段对液滴过冷状态的影响显著强于准一维传热阶段，三维收缩效应对液滴过冷状态起决定性作用。

3) 在典型试验工况下，当试验段气流速度为76 m/s时，粒径小于200 μm的液滴均过冷(液滴气流温度差小于2 ℃)，当试验段气流速度为157 m/s时，粒径小于40 μm的小液滴仍然过冷(液滴气流温度差小于1.1 ℃)，但粒径大于100 μm的大液滴已不再过冷(液滴气流温度差大于5 ℃)。

需要指出的是，由于结冰风洞中气液两相运动过程十分复杂，涉及多物理场的耦合相互作用，同时伴随复杂的传热传质过程，而本文发展的气液两相耦合计算方法则是基于一些假设下的简化分析方法，尤其忽略了液滴传质过程的影响，导致本文计算结果与工程实际存在一定程度的偏差。因此本文对结冰风洞液滴过冷状态的评估结果较为保守，同时，建立考虑液滴相变过程的两相耦合计算方法并开展验证试验则是下一步的工作。

[1] 林贵平, 卜雪琴, 申晓斌, 等. 飞机结冰与防冰技术[M]. 北京: 北京航空航天大学出版社， 2016: 6-28.

LIN G P, BU X Q, SHEN X B, et al. Aircraft icing and anti-icing technology[M]. Beijing: Beihang University Press, 2016: 6-28 (in Chinese).

[2] 易贤. 飞机积冰的数值计算与积冰试验相似准则研究[D]. 绵阳: 中国空气动力研究与发展中心, 2007: 6-17.

YIN X. Numerical computation of aircraft icing and study on icing test scaling law[D]. Mianyang: China Aerodynamics Research and Development Center, 2007: 6-17 (in Chinese).

[3] 李伟斌, 易贤, 杜雁霞, 等. 基于变分分割模型的结冰冰型测量方法[J]. 航空学报, 2017, 38(1): 120167.

LI W B, YI X, DU Y X, et al. A measurement approach for ice shape based onvariational segmentation model[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(1): 120167 (in Chinese).

[4] 易贤, 朱国林, 王开春, 等. 结冰风洞试验水滴直径选取方法[J]. 航空学报, 2010, 31(5): 877-882.

YI X, ZHU G L, WANG K C, et al. Selection of water droplet diameter in icing wind test[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(5): 877-882 (in Chinese).

[5] 易贤, 桂业伟, 朱国林. 飞机三维结冰模型及其数值求解方法[J]. 航空学报, 2010, 31(11): 2152-2158.

YI X, GUI Y W, ZHU G L. Numerical method of a three-dimensional ice accretion model of aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(1): 2152-2158 (in Chinese).

[6] VAN ZANTE J F, IDE R F, STEEN L E. NASA Glenn icing research tunnel: 2012 cloud calibration procedure and results[C]∥4th AIAA Atmospheric and Space Environments Conference. Reston,VA : AIAA, 2012.

[7] STEEN L E, IDE R F, VAN ZANTE J F, et al. NASA Glenn icing research tunnel: 2014 and 2015 cloud calibration procedures and results: NASA/TM-2015-218758[R]. Washington, D.C.: NASA, 2015.

[8] MILLER D R, ADDY H E, IDE R F. A study of large droplet ice accretions in the NASA Glenn IRT at near-freezing conditions: NASA TM-1996-107142-REV1[R]. Washington, D.C.: NASA, 1996.

[9] WILLBANKS C E, SCHULZT R J. Analytical study of icing simulation for turbine engines in altitude test cells[J]. Journal of Aircraft, 1975, 12(12): 960-967.

[10] RAGNI A, ESPOSITO B, MARRAZZO M, et al. Calibration of the CIRA IWT in the high speed configuration[C]∥43th AIAA Aerospace Science Meeting and Exhibit. Reston, VA: AIAA, 2005.

[11] BELLUCCI M, ESPOSITO B M, MARRAZZO M, et al. Calibration of the CIRA IWT in the low speed configuration[C]∥45th AIAA Aerospace Science Meeting and Exhibit. Reston, VA: AIAA, 2007.

[12] TAN S C, PAPADAKIS M. General effects of large droplet dynamics on ice accretion modeling[C]∥41th AIAA Aerospace Science Meeting and Exhibit. Reston, VA: AIAA, 2003.

[13] 易贤, 马洪林, 王开春, 等. 结冰风洞液滴运动及传质传热特性分析[J]. 四川大学学报, 2012, 44(2): 132-135.

YI X, MA H L, WANG K C, et al. Analysis of water droplet movement and heat/mass transfer in an icing wind tunnel[J]. Journal of Sichuan University, 2012, 44(2): 132-135 (in Chinese).

[14] DU Q, WANG Z Z, ZHU C L. Analysis and calculation of droplet-air mixed phase flow model in icing wind tunnel[C]∥32nd AIAA Aerodynamic Measurement Technology and Ground Testing Conference. Reston, VA: AIAA, 2016.

[15] GARCIA-CASCALE J R, MULAS-PEREZ J, PAILLERE H. Extension of some numerical schemes to the analysis of gas and particle mixtures[J]. International Journal for Numerical Methods in Fluids, 2008, 56: 845-875.

[16] SAITO T. Numerical analysis of dusty-gas flows[J]. Journal of Computational Physics, 2002, 176: 129-144.

[17] LUO X S, WANG G, OLIVIER H. Parametric investigation of particle acceleration in high enthalpy conical nozzle flows for coating applications[J]. Shock Waves, 2008, 17: 351-362.

[18] 吴孟龙, 常士楠, 冷梦尧, 等. 基于欧拉法模拟旋转帽罩水滴撞击特性[J]. 北京航空航天大学学报, 2014, 40(9): 1263-1267.

WU M L, CHANG S N, LENG M Y, et al. Simulation of droplet impingement characteristics of spinner based on Eulerian method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(9): 1263-1267 (in Chinese).

[19] RANZ W E, MARSHALL W R. Evaporation from drops—Part Ⅱ[J]. Chemical Engineering Progress, 1952, 48(4): 173-180.

[20] 郭向东, 黄生洪, 吴颖川, 等. 氢燃料燃烧加热风洞中水蒸气相变效应的数值研究[J]. 推进技术, 2017, 38(4): 932-941.

GUO X D, HUANG S H, WU Y C, et al. Numerical evaluation of water vapor phase transition effects in a hydrogen-fueled combustion-heated wind tunnel[J]. Journal of Propulsion Technology, 2017, 38(4): 932-941 (in Chinese).

[21] COBER S, BERNSTEIN B, JECK R, et al. Data and analysis for the development of an engineering standard for supercooled large drop conditions: DOT/FAA/AR-09/10[R]. Washington, D.C.: DOT/FAA/AR, 2009.

[22] WONG S C, TAN S C, PAPADAKIS M. Spray rig design for airborne icing tankers[C]∥45th AIAA Aerospace Sciences Meeting and Exhibit. Reston, VA: AIAA, 2007.

Numericalstudyofsupercoolingcharacteristicsofdropletinicingwindtunnel

GUOXiangdong1,2,*，WANGZixu2，LIMing2，XIAOChunhua2

1.StateKeyLaboratoryofAerodynamics,ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China2.KeyLaboratoryofAircraftIcingandAnti/De-Icing,ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China

Inordertounderstandthesupercoolingofthedropletintheicingwingtunnel,anumericalmethodbasedonEuleriantheoryisdevelopedtosimulatethegas-dropletflowinanicingwindtunnel.Usingthenumericalmethod,aparametricstudyisfirstlyconducted,thentheinfluenceof3Dcontractionofatypicalicingwindtunnelconfigurationisinvestigated,andfinallythesupercoolingofthedropletinthetestsectionofthewindtunnelisevaluated.Theresultsshowthatthedropletdiameterandgasvelocityhaveagreateffectonthesupercoolingofthedroplet.Thelargerthedropletdiameterorairspeed,thelargerdistancewherethedroplettemperatureisclosetothegastemperature.Theprocessofdropletheattransferinatypicalicingwindtunnelconfigurationcanbedividedintotwostagesthequasi-1Dstageandthe3Dcontractionstage.Theinfluenceofthe3Dcontractionstageonthedropletsupercoolingisgreaterthanthatofthequasi-1Dstage.Therefore,the3Dcontractionofthetypicalicingwindtunnelconfigurationhasasignificanteffectonthesupercoolingofthedroplet.Intypicaltestconditions,thesmalldropletswiththediametersmallerthan40μmaresupercooling(thetemperaturedifferencebetweendropletandgasislowerthan2℃)inthetestsection,butbigdropletswiththediameterbiggerthan100μmcannotbesupercooling(thetemperaturedifferencebetweenthedropletandgasishigherthan5℃)atthehightestsectionvelocity(theairspeedis157m/s).

aircrafticing;icingwindtunnel;droplet;supercooling;numericalsimulation

2017-03-18；Revised2017-03-24；Accepted2017-04-19;Publishedonline2017-04-251422

URL：http://hkxb.buaa.edu.cn/CN/html/20171008.html

s：NationalBasicResearchProgramofChina(2015CB755800)；NationalNaturalScienceFoundationofChina(11572338)

.E-maileasterkuo@163.com

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.121254

V221.3

A

1000-6893(2017)10-121254-09

2017-03-18；退修日期2017-03-24；录用日期2017-04-19；< class="emphasis_bold">网络出版时间

时间：2017-04-251422

http://hkxb.buaa.edu.cn/CN/html/20171008.html

国家“973”计划(2015CB755800)；国家自然科学基金(11572338)

.E-maileasterkuo@163.com

郭向东，王梓旭，李明，等．结冰风洞中液滴过冷特性数值研究J． 航空学报,2017,38(10):121254.GUOXD,WANGZX,LIM,etal.NumericalstudyofsupercoolingcharacteristicsofdropletinicingwindtunnelJ.ActaAeronauticaetAstronauticaSinica,2017,38(10):121254.

(责任编辑：李明敏)