再入飞行器沉浮特性近似解析及应用
顾杰,张曙光,*,杨帆,王保印
1.北京航空航天大学 交通科学与工程学院,北京 100083 2.成都飞机设计研究所,成都 610091
再入飞行器沉浮特性近似解析及应用
顾杰1,张曙光1,*,杨帆2,王保印1
1.北京航空航天大学 交通科学与工程学院,北京 100083 2.成都飞机设计研究所,成都 610091
采用基于平衡滑翔的数值或解析预测-校正再入制导方法的再入飞行器,从初始下降段到平衡滑翔段过渡或出现较大预测偏差时易产生沉浮振荡,且随着近年来所研究飞行器升阻比的增加,沉浮振荡更加明显,从而引起了研究者对高超声速沉浮特性的重新审视。首先,通过三阶纵向动态方程及平衡滑翔条件推导出了形式简洁、能直观表达主要影响因素的再入飞行器高超声速沉浮特性近似解。在此基础上,分析发现高超声速沉浮阻尼特性随高度的变化规律主要由轨道速度比和沉浮修正参数主导,澄清了以往对大气密度梯度参数影响的猜测。最后,推导出再入轨迹振荡抑制器设计的近似解析关系,进一步完善了基于平衡滑翔的数值或解析预测-校正再入制导方法,仿真验证表明该方法能够有效抑制再入轨迹的沉浮振荡。
再入;高超声速飞行器;沉浮;阻尼;解析解
近十多年来,基于平衡滑翔的数值或解析预测-校正再入制导方法,以其良好的自适应性得到了越来越多的关注[1-11]。该方法设计过程简洁,不需要像传统的航天飞机再入制导方法[12]一样预先精心设计依赖于任务的参考剖面,因而能够节省大量人力物力。但是预测-校正制导方法在出现较大的模型偏差或遇到黑障区较大的导航误差[13-14]时,将产生较大的校正偏差,从而使得再入轨迹偏离平衡滑翔状态,进而引起沉浮振荡,特别是从初始下降段到平衡滑翔段过渡时最为明显[3-4]。这些不确定性较大的轨迹振荡可能会导致飞行器超出气动热、动压和过载等约束限制,从而使得热防护结构和乘员面临危险[2,15]。
为消除以上再入飞行过程中因沉浮振荡产生的安全风险,Lu[1-4]、Shen[10-11]和Xue[7]等在寻找有效消除再入轨迹沉浮振荡的自适应方法上进行了大量工作,并得到了有益的结果[4]。Shen通过预测搜索得到了再入初始下降段与平衡滑翔段平滑过渡的转换点信息[10-11]。Xue则在Shen的基础上引入与地球自转相关的修正因子进一步提高了再入轨迹的平滑性[7]。但以上方法均是基于模型的预测控制,其控制效果依赖于模型计算的准确性。而Lu[1-4]则在多年工作的基础上采用简洁的反馈控制抑制了再入轨迹振荡,但是其反馈增益是依据经验设定的,缺乏较为直接的理论依据。因而为了从理论上完善Lu的沉浮振荡抑制方法,且随着近年来对易于产生沉浮振荡的中高升阻比高超声速飞行器研究的增多[4,16-18]和相关问题的显现[3-4],以及近期在火星滑翔再入研究中升力飞行器易于跳跃问题的出现[19],使得高超声速飞行器沉浮振荡特性的研究重新受到了关注和审视[20-21]。
航空发展早期,“沉浮”(Phugoid)一词最早是英国学者Lanchester[22]于1908年在研究低速飞机飞行稳定性时提出的,其将低速飞机水平飞行时相对较慢的轨迹俯冲上仰运动命名为“沉浮”运动。Lanchester在迎角近似为常值和切向力平衡的假设下,依据机械能守恒推导出了低速飞机沉浮模态周期的简洁解析表达式,表明低速飞机沉浮模态的周期仅与飞行速度有关。但由于Lanchester方法未考虑能量耗散,故无法得到任何阻尼信息。此后,文献[23-26]分别推导出了较为准确的低速飞机沉浮模态特征根或特征方程系数的解析表达式;而Etkin[23]则得到了最有直观指导意义的结果,其所得解析解表明低速飞机的沉浮阻尼比完全由升阻比大小和动力系统类型确定。
研究低空低速飞行时,可认为大气密度近似不变以及大气具有不可压缩性。但对于中高空高速飞行则需要考虑大气密度和压缩性的影响。Scheubel[27]于1942年在Lanchester研究基础上考虑了大气密度随高度变化的影响;Neumark[28]还考虑了压缩性影响,推导出复杂但较为准确的超声速飞行沉浮模态特征根近似解析表达式。
随着高超声速飞行器的发展,Etkin[29]于1961年首次发表采用直接数值方法的高超声速纵向飞行动力学研究结果,指出该研究必须考虑大气密度随高度变化和由地球曲率产生的“离心力”的影响,且在接近轨道速度时重力随高度变化的影响会显著起来。由Etkin的数值结果可以看出高超声速飞行的沉浮周期随高度增加而增加,并趋近于对应高度的轨道周期,但不受推力规律的影响;而沉浮阻尼特性则对推力规律较为敏感。Etkin通过对沉浮阻尼特性随高度变化曲线和大气密度梯度参数随高度变化曲线的对比,认为高超声速飞行器在90多千米高度处出现“重阻尼”是由于大气密度梯度参数的绝对值在该高度出现峰值导致的,后面将对这一看法作较深入讨论。
为了显式表达各种参数对高超声速飞行器沉浮特性的影响,Laitone和Chou[30]推导出了常值推力下高超声速飞行器沉浮周期和阻尼项的近似解析表达式;Vinh和Dobrzelecki[31]则通过引入一个由拉格朗日展开法求解出的无穷级数,对Laitone和Chou的结果进行了修正,表达式更加准确,但是也变得更加复杂。
20世纪80年代末,随着以超燃冲压发动机为关键技术的美国国家空天飞机计划(National Aero-Space Plane,NASP)的启动,部分学者开始了关于推力规律对高超声速飞行器纵向动力学特性影响的深入研究。Berry[32]认为空天飞机二阶变化的推力对沉浮模态和高度模态具有显著影响;Markopoulos等[33]则进行了随速度、高度变化而变化的推力对高超声速沉浮特性的影响研究,结果表明当推力规律函数为相关参数一阶及一阶以下变化律时,高超声速飞行器沉浮周期不受推力规律影响,这与Etkin和Berry的结论一致。
对于高超声速滑翔再入研究,Ferreira[34]以及Chen等[20]分别采用Liouville变换和通用多尺度理论求解出了滑翔再入沉浮运动轨迹的解析表达式(由平衡滑翔项和阻尼振荡项组成)和整个再入过程轨迹振荡次数的表达式,两者结果基本相同;胡锦川和陈万春[21]则在进行平稳滑翔弹道研究过程中通过高度偏差的二阶微分方程,得到了滑翔再入沉浮振荡的自然频率和阻尼比的近似解析表达式,但是滑翔再入纵向沉浮运动为三阶动态系统,故其近似解析解的精度还有提高的空间。
综上所述,迄今对飞行器沉浮运动特性的研究已经相对全面。但是已有的高超声速沉浮特性解析式均较复杂,还没有像Etkin等所推导出的低速飞机沉浮特性解析式一样具有直观指导意义的简洁结果,因而不易理解再入飞行器沉浮特性随再入轨迹的变化规律及影响因素。为此,本文在已有研究基础上,利用平衡滑翔条件,推导出再入飞行器沉浮运动特性的简洁近似解析式,并在沉浮特性规律解释和轨迹振荡抑制两方面进行了应用,其对于再入运动分析与控制设计均具有指导意义。
1 再入运动方程
1.1 非线性再入运动方程
为进行较为精确的飞行器再入运动分析和仿真计算,考虑地球自转引起的向心加速度和科氏加速度、地球曲率引起的向心加速度等相关项,且认为地球大气是静止的,即地球大气随地球以相同角速度自转,则均质圆地球条件下的三自由度再入质点运动方程为[7]
(1)
(2)
(3)
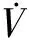
(4)
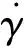
(5)
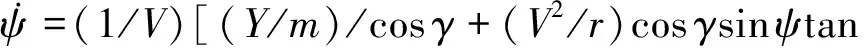
(6)
式中:m为再入飞行器的质量;r为地球球心到飞行器质心的距离;g=μ/r2为重力加速度,μ=3.986 031 954×1014m3/s2为地球引力常数[35-36];Ω为地球自转角速度;θ和φ分别为地球经度和纬度;V为飞行器相对地球表面的速度;γ为航迹角(飞行器速度矢量高于当地水平面为正);ψ为航向角(飞行器速度矢量从北向开始顺时针为正);X、Y和Z为除重力外作用于飞行器上的合力在3个方向上的分量,分别为切向力(沿速度方向为正)、侧向力(垂直于速度矢量所在的铅垂面向右为正)和法向力(垂直于速度矢量向下为正)。对于无动力再入飞行器来说,X、Y和Z可以表示为
(7)
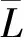
ρ=ρreβ(r-Re)
(8)
式中:ρr为参考大气密度;β=(∂ρ/∂r)/ρ为大气密度高度变化率与当地大气密度的比值,简称大气密度梯度参数;Re=6 371.2×103m为地球平均半径。
图1直观给出了0~180 km高度下几种大气密度梯度参数β的值,其中实线依据1966年美国标准大气拟合数据得到[31,34],其他3种线型是为了便于对比分析β的影响而给出的,β通常取为常值,本文中若无特别说明,取以下常值[29,35-36](图1点划线,最接近真实情况):
(9)
式中:hr为大气密度梯度参数的参考高度。
本文选用航天飞机轨道器作为算例飞行器,其再入质量和气动参考面积分别为80 000 kg和249.91 m2[36]。考虑到高超声速飞行气动系数的Oswatitsch马赫数无关性原理[29],其高超声速升力系数和阻力系数可近似拟合为[36]
(10)
式中:α为迎角。
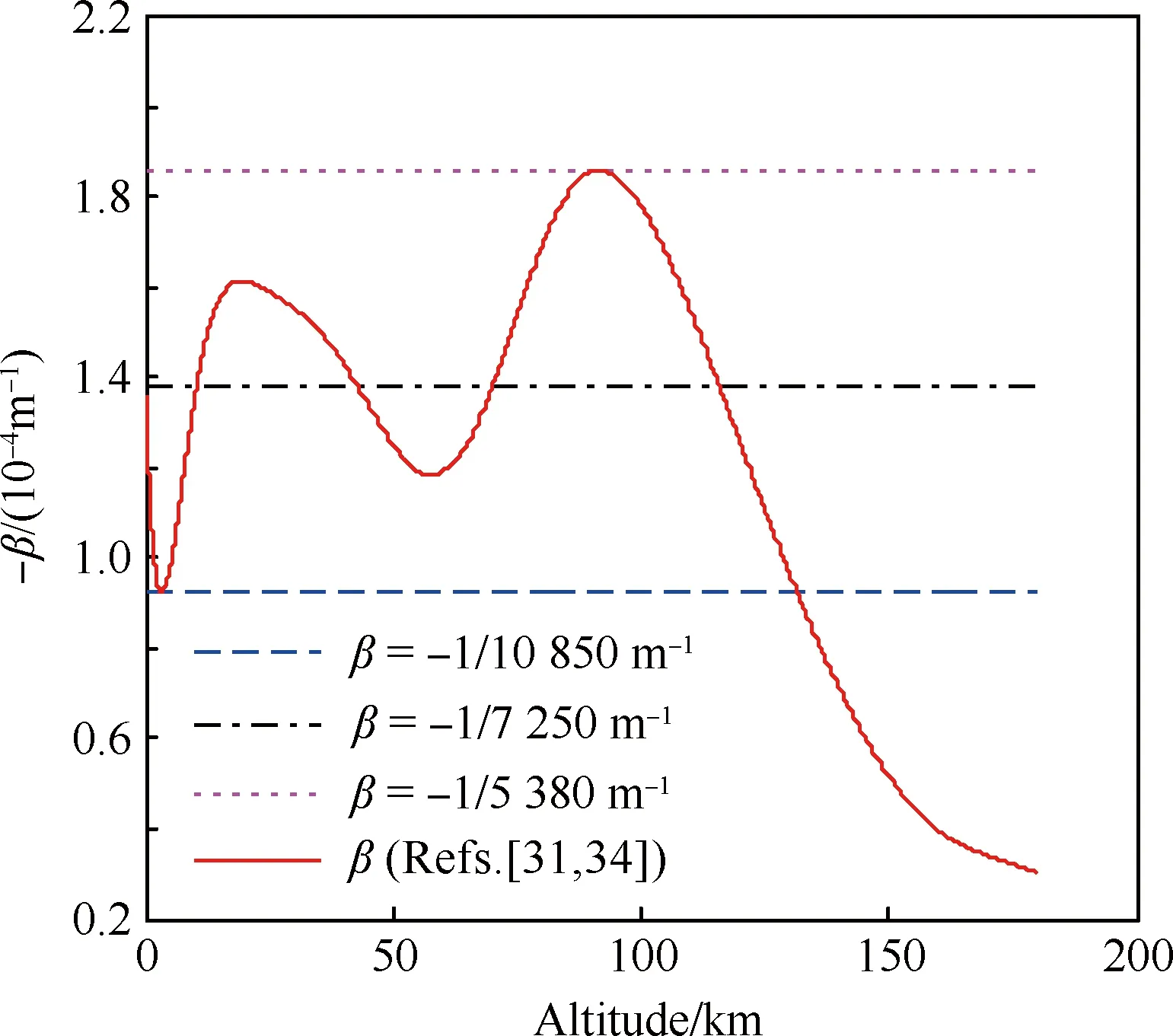
图1 地球大气密度梯度参数 Fig.1 Density-gradient parameters of Earth’s atmosphere
1.2 线性再入沉浮动态方程
飞行器再入时地球自转引起的向心加速度特征量仅占重力加速度的0.35%,随速度增加而增加的科氏加速度特征量在轨道速度时也不超过重力加速度的10%,因而在进行初步再入运动分析时忽略地球自转不会对分析结果产生较大影响[29],且数值分析也表明忽略地球自转对沉浮动态特性影响很小,故可令Ω=0,代入式(1)、式(4)和式(5)得到再入沉浮动态方程为
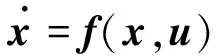
(11)
式中:x=[Vγr]T和u=[kσ]=[cosσ]分别为状态向量和控制向量。
Ferreira[34]和Chen等[20]的研究已经表明,滑翔再入沉浮运动由平衡滑翔项和阻尼振荡项组成,因而可取平衡滑翔状态为基准状态,并可由Ferreira[34]和Chen等[20]推导的平衡滑翔近似解得到。在基准状态对再入沉浮动态方程进行李雅普诺夫线性化[37-38],即可得到线性再入沉浮动态方程为
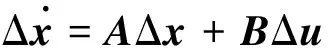
(12)
(13)
B=[0 -Zkσ/(mV) 0]T
(14)
式中:前缀Δ表示扰动量;Δx=[ΔVΔγΔr]T为状态向量;Δu=[Δkσ]为控制向量;A为状态矩阵;B为控制矩阵;A13、A21和A23分别为
(15)
飞行器高超声速再入飞行时,由于气动系数具有马赫数无关性,因而气动力主要由迎角决定。而迎角为短周期参数,其相对于缓慢变化的沉浮运动来说可以认为是常值。故高超声速飞行时的纵向气动导数可表示为
(16)
2 再入沉浮特性参数一次近似
2.1 特征方程
鉴于中高升阻比飞行器平衡滑翔再入过程中航迹角及航迹角变化率都很小[34],故在对以平衡滑翔状态为基准状态的线性再入运动方程推导分析时均将其近似取为零,于是可得到特征方程为
|λI-A|=λ3+C1λ2+C2λ+C3=0
(17)
式中:λ为特征值;
(18)
根据Etkin[29]的数值研究,高超声速飞行具有振荡沉浮模态和单调纵向螺旋模态(高度模态)。其特征方程具有一对共轭复根和一个离原点很近的实根,共轭复根可表示为

(19)
式中:η为阻尼项;ζ为阻尼比;ω为阻尼振荡频率;ωn为无阻尼振荡频率,即自然频率。
特征方程式(17)还可表示为
(λ2+p1λ+p2)(λ-λ3)=0
(20)
式中:
(21)
2.2 阻尼振荡频率
特征方程式(17)中常数项C3的主导项表征阻力的变化,也即切向力变化率项。Etkin[29]关于火箭动力(推力为常值)和吸气式动力(推力与密度成正比)高超声速飞行器沉浮周期的数值研究表明,切向力变化对沉浮周期影响微弱[29-30],因而可以忽略C3项求解近似沉浮周期[30],则有λ3=0、p1=C1和p2=C2,于是特征根虚部(即阻尼振荡频率)可表示为
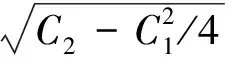
(22)
考虑到平衡滑翔条件Z/m+g=V2/r,经适当变形整理,得沉浮模态阻尼振荡频率解析式为
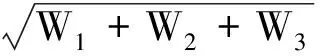
(23)
式中:
(24)
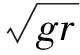
2.3 阻尼项
阻力是再入飞行器沉浮运动中消耗能量的唯一来源,因而也是沉浮运动阻尼的根本来源,故不能通过忽略含阻力相关项的特征方程得到准确的阻尼项解析式。下面对原三阶特征方程进行推导,将式(20)展开后与式(17)对比可得
C1=p1-λ3=-2η-λ3=2ζωn-λ3
(25)
(26)
(27)
由式(25)、式(27)可得到沉浮模态特征根实部(即阻尼项)的解析式为
(28)

(29)
式中:无量纲沉浮修正参数f的解析式为
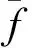
(30)
2.4 自然频率、阻尼比和半衰期内振荡次数
由式(23)和式(29)可依次得到沉浮模态自然频率、阻尼比、半衰期内振荡次数的解析式为
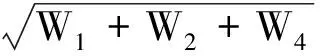
(31)

(32)
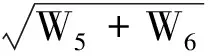
(33)
式中:
(34)
至此,基于平衡滑翔条件和阻力变化量对周期影响微弱的特点,建立了表征再入沉浮运动特性的自然频率、阻尼比两个基本参数的一次近似解析式(31)和式(32),以及阻尼振荡频率、阻尼项和半衰期内振荡次数的一次近似解析式(23)、式(29)和式(33)。
2.5 高超声速沉浮近似解析式的低空低速适用性
研究低空低速飞行时,来流可认为是不可压缩流,地球曲率引起的“离心力”可忽略,大气密度梯度参数可取为β=0,低速情况下轨道速度比也可近似取为U≈0。则将高超声速再入沉浮阻尼振荡频率解析式(23)和自然频率解析式(31)展开,并将β=0和U≈0代入,可推导出低空低速飞行沉浮运动阻尼振荡频率和自然频率的近似简化解析式为
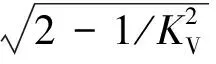
(35)
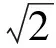
(36)
由式(30)可知,当U≈0时,有f≈0。于是由式(29)可得到低空低速飞行沉浮运动阻尼项(特征根实部)的近似简化解析式为
η≈-g/(KVV)
(37)
展开式(32)和式(33),并将β=0、U≈0和f≈0代入,可得低空低速飞行沉浮运动阻尼比和半衰期内振荡次数的近似简化解析式为
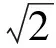
(38)
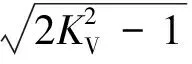
(39)
以上低空低速飞行沉浮特性参数近似简化解析式的推导结果均与Lanchester[22]、Etkin[23]以及方振平[38]等的经典结果一致,这是表明所推导的高超声速再入沉浮特性近似解析式正确性的必要条件,但并不充分。后续将在对解析式二次近似的推导分析过程中,与由状态矩阵式(13)得到的数值解进行统一数值对比,以充分验证所推导的高超声速再入沉浮特性近似解析式的正确性。
3 再入沉浮特性参数二次近似
第2节推导的一次近似解析式,包含的影响因素关系仍显繁琐,本节在数值比较的基础上,通过忽略高超声速段的小量进行二次近似简化。
3.1 简化的数值分析基础
图2直观表示出不同纵向升阻比下W2、W3、W4与W1的相对大小关系,结合式(23)、式(31)和式(32),可以看出在大部分高超声速情况下,W1为阻尼振荡频率、自然频率和阻尼比的主导项之一,因而可以忽略W2、W3和W4。
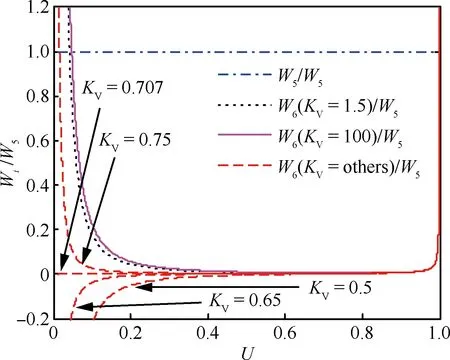
图3直观表示出不同纵向升阻比下W6与W5的相对大小关系,KV=1.5和KV=100的两条曲线表明当KV>1.5时,W6对纵向升阻比不敏感,并且结合式(33)可以看出在大部分高超声速情况下,W5为表征阻尼特性的半衰期内振荡次数的主导项之一,因而可忽略W6。
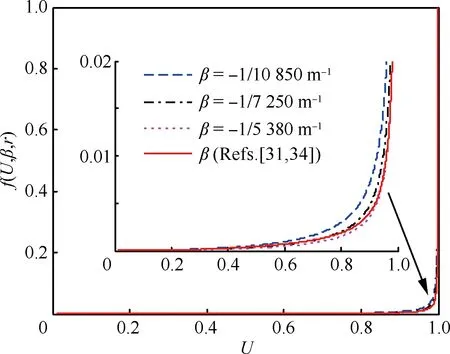
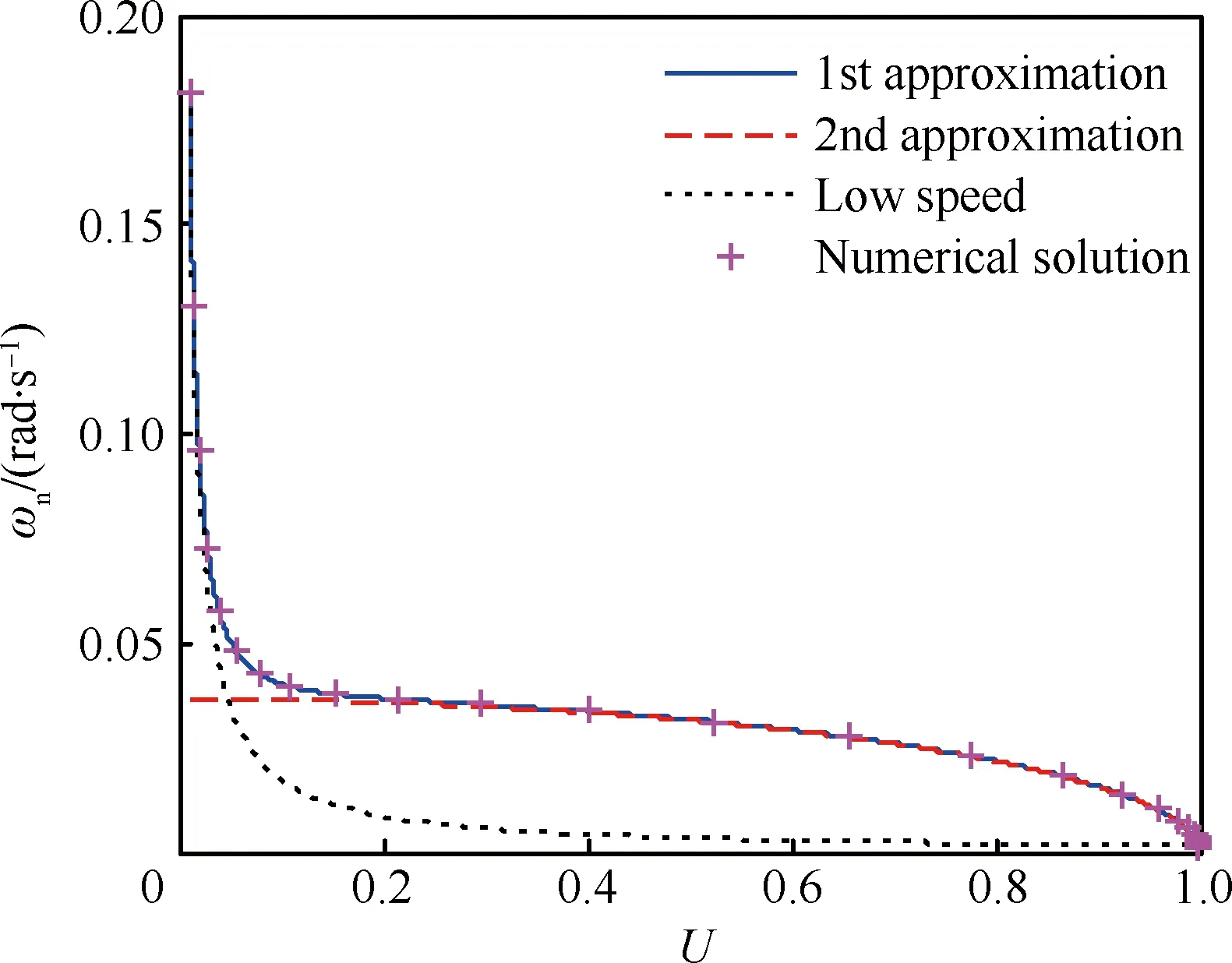
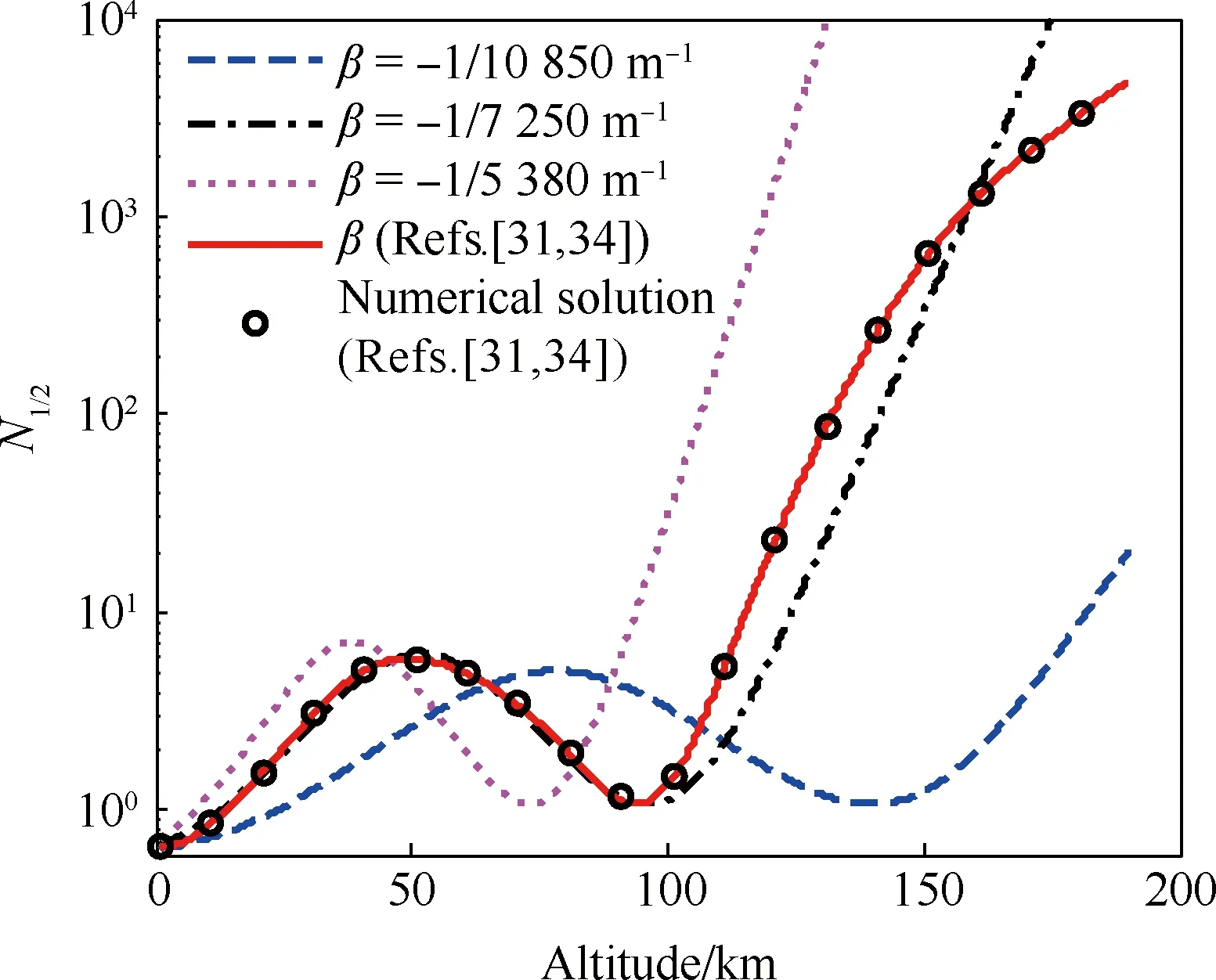
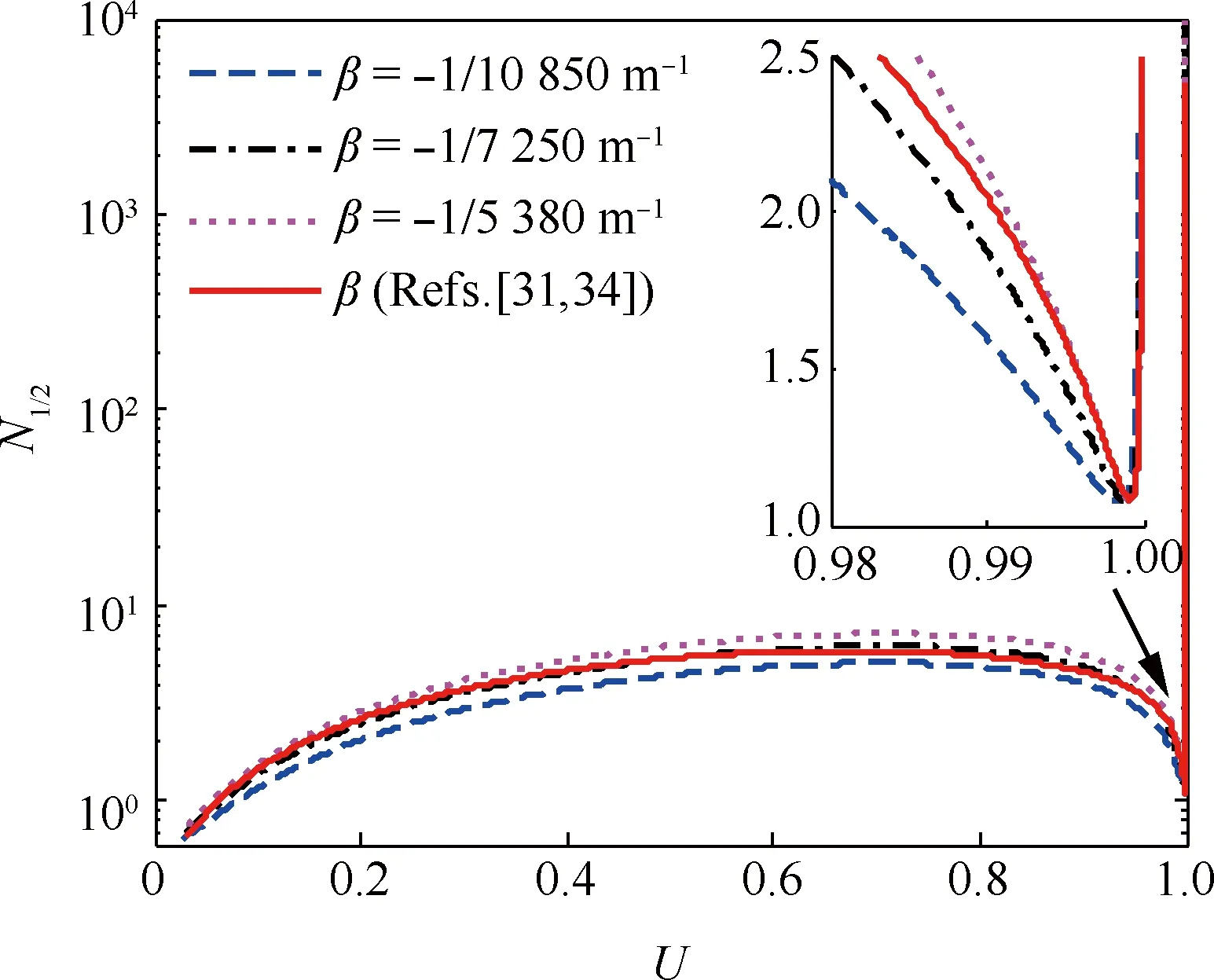
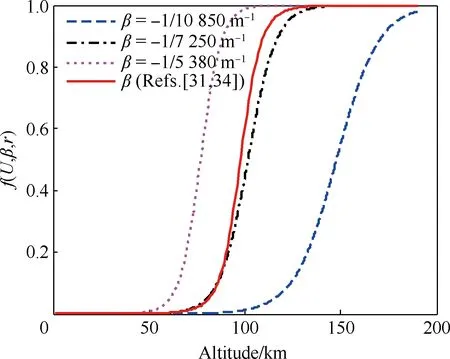
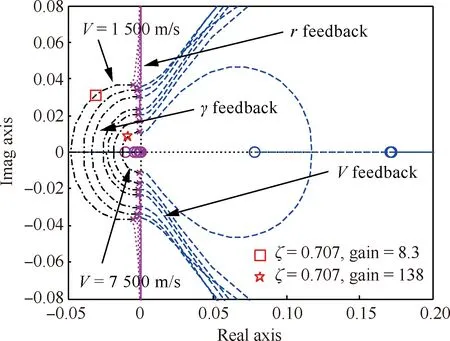
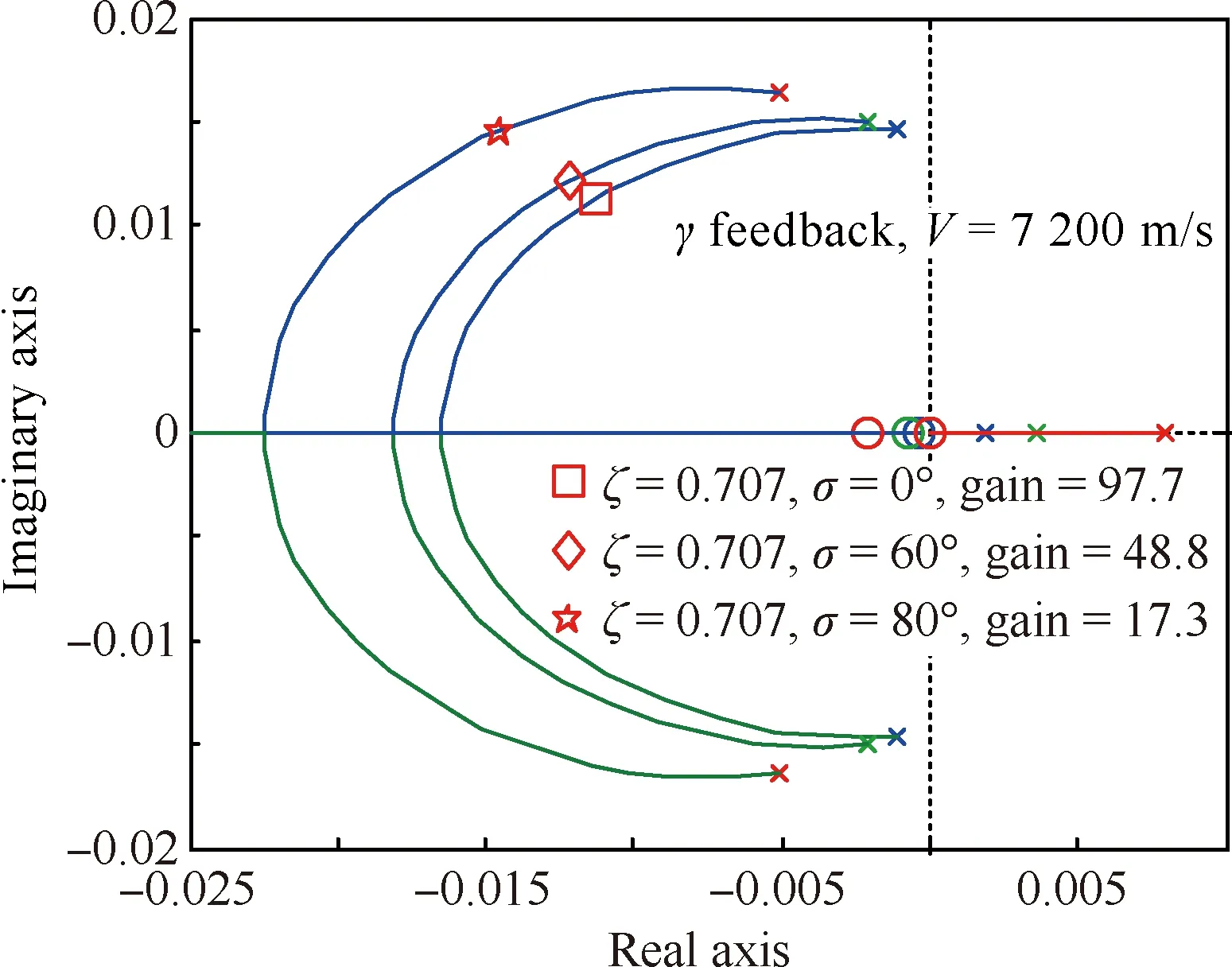
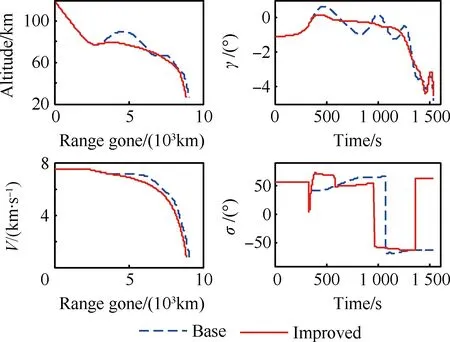
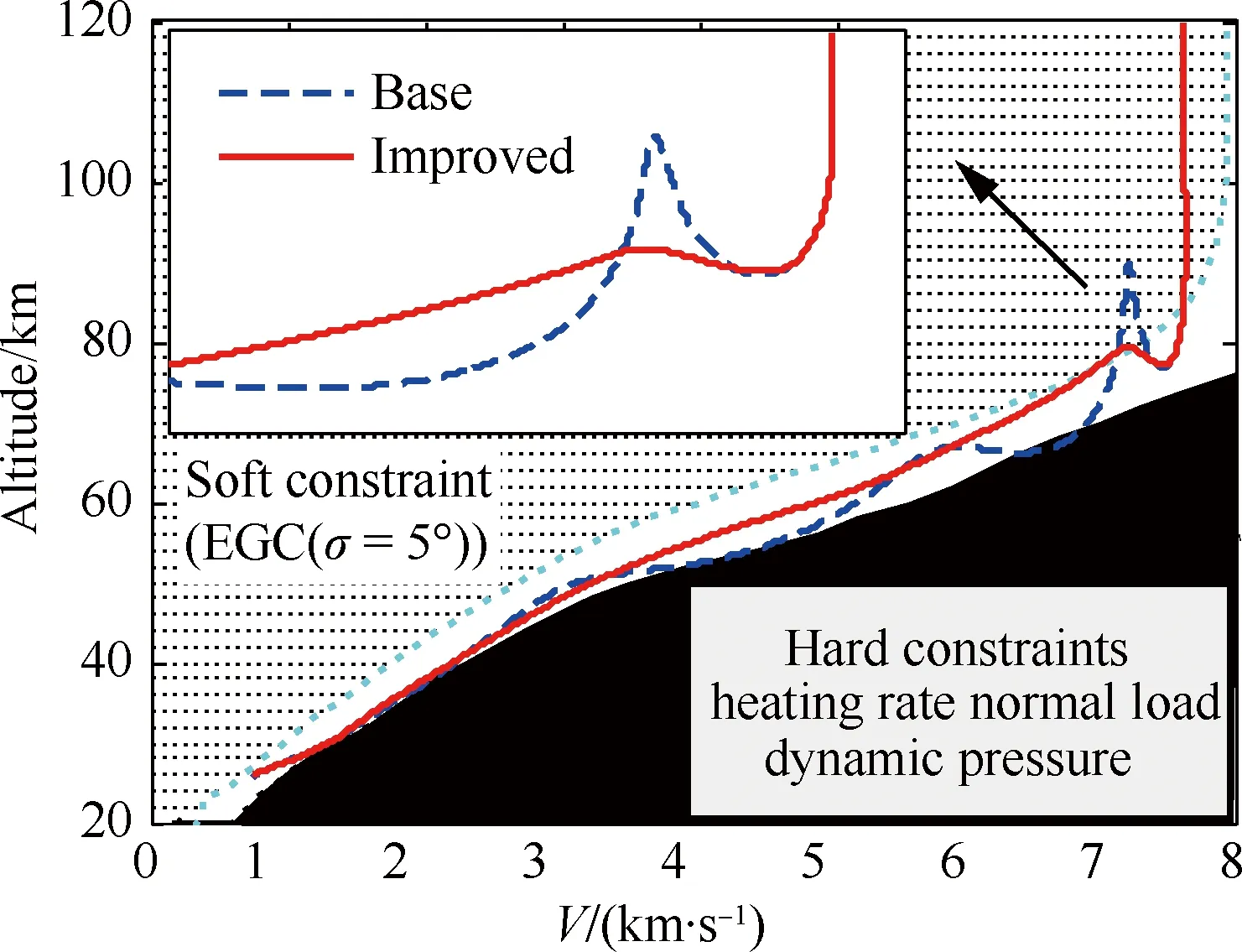
图4直观表示出了作为轨道速度比U、大气密度梯度参数β和高度r的函数的沉浮修正参数f在不同β取值下随速度的变化情况,可以看出当轨道速度比U<0.98,即飞行速度V<0.98Vc时,有0 图2 Wi/W1(i=1,2,3,4)随轨道速度比的变化Fig.2 Wi/W1(i=1,2,3,4) vs the ratio of flight speed to orbital speed 图3 Wi/W5(i=5,6)随轨道速度比的变化Fig.3 Wi/W5(i=5,6) vs the ratio of flight speed to orbital speed 图4 沉浮修正参数随轨道速度比的变化Fig.4 Phugoid correction factor vs the ratio of flight speed to orbital speed 3.2 阻尼项二次近似解析式 由3.1节数值分析结果,忽略式(29)中的f,可得到高超声速再入沉浮阻尼项(特征根实部)的二次近似简化解析式为 η≈-g/(KVV) (40) 式(40)与低空低速式(37)完全相同,表明与低空低速飞行器一样,高超声速飞行器纵向升阻比越大其沉浮阻尼越小,并且高超声速沉浮阻尼项与速度的反比关系从形式上决定了弱沉浮阻尼是中高升阻比高超声速飞行器的固有特性。 不过从本质上看,这一固有特性源于高空很小的大气密度。因为阻尼主要来源于气动阻力随速度的变化,而由其表达式 dD/dV=∂D/∂V+(∂D/∂ρ)(dρ/dr)(dr/dV)≈ ∂D/∂V=ρVSCD (41) 可知,由于大气密度随高度呈指数减小,使ρV值沿着平衡滑翔轨迹随着高度和速度增加反而快速减小,从而导致高超声速飞行器具有了弱阻尼的固有特性。 3.3 自然频率二次近似解析式 根据数值分析结果,忽略式(23)、式(31)中的W2、W3和W4,则高超声速再入沉浮阻尼振荡频率与自然频率近似相等(间接表明沉浮阻尼比很小),再考虑到平衡滑翔条件可得出高超声速再入沉浮自然频率的二次近似简化解析式为 (42) 图5中对自然频率一次近似解式(31)、二次近似解式(42)、低空低速近似解式(36)和由状态矩阵式(13)得到的数值解进行了对比,验证了所推导解析式的正确性,并表明二次近似解在高超声速飞行段(U>0.2)的精度很好。由式(42)可知高超声速再入沉浮运动的自然频率主要由轨道速度比U和与飞行器特性无关的大气密度梯度参数β、重力加速度g决定,因而不同飞行器高超声速沉浮自然频率随轨道速度比的变化情况相差不大。 由式(42)可得到沉浮运动等效弹性系数为 (43) 式(43)表明高超声速再入沉浮振荡的恢复力主要来源于随高度变化的纵向平面升力变化量。 图5 沉浮自然频率随轨道速度比的变化Fig.5 Phugoid natural frequency vs the ratio of flight speed to orbital speed 3.4 阻尼比和半衰期振荡次数二次近似解析式 依据简化的数值分析结果,忽略式(32)中f、W2和W4,以及式(33)中的f和W6,可分别得到高超声速再入沉浮阻尼比和半衰期内振荡次数的二次近似简化解析式为 (44) (45) 图6中将阻尼比一次近似解式(32)、二次近似解式(44)、低空低速近似解式(38)、由状态矩阵式(13)得到的数值解和由胡锦川和陈万春[21]通过高度偏差的二阶微分方程推导出的近似解进行了对比,验证了所推导解析式的正确性,且可以看出本文的阻尼比二次近似解式(44)在除轨道速度外的高超声速飞行段(0.2 二次近似解式(44)中,由于-βr≈900,当0.2≤U≤0.98时,有0.066 7/KV≤ζ≤0.17/KV,可见纵向升阻比KV和轨道速度比U是沉浮阻尼特性的主导影响参数,同时表明低阻尼比是中高升阻比高超声速飞行器再入沉浮运动的固有特性,且纵向升阻比越大阻尼比越小。 综合式(40)和式(44)的分析可知,再入飞行器在高超声速滑翔时具有弱阻尼和低阻尼比的固有特性,且作为飞行器本体参数的升阻比对其也具有重要的主导作用(与频率不同),同时其反比关系也解释了随升阻比增大高超声速飞行器越易产生沉浮振荡的原因。 图6 沉浮阻尼比随轨道速度比的变化Fig.6 Phugoid damping ratio vs the ratio of flight speed to orbital speed 本节对以上所推导的沉浮特性近似解及近似关系分别在沉浮特性规律的解释和轨迹振荡的抑制方面进行了应用。 4.1 高超声速沉浮阻尼特性规律解释 表征高超声速沉浮阻尼特性的半衰期内振荡次数N1/2随高度变化的曲线(图7圆圈)和大气密度梯度参数β随高度变化的曲线(图1实线)具有相似的变化规律,很容易让人产生两者具有强相关性的认识。最早进行高超声速飞行动力学数值研究的Etkin认为,高超声速飞行器在90多千米高度处出现“重阻尼”(N1/2出现极小值)是由于大气密度梯度参数β的绝对值在该高度出现峰值导致的[29]。但通过解析分析和数值验证,均表明此观点不准确。以下进行详细说明,并应用所推导的近似解分析其变化规律的主导因素。 首先,由所推导的高超声速沉浮运动近似式(45)可以看出,β绝对值越大,N1/2越大(即沉浮阻尼越弱),而不是Etkin推测的阻尼越重。 其次,为便于同Etkin的数值结果进行对比,图7选用了与Etkin相同的飞行器模型。图中圆圈为通过状态矩阵式(13)得到的数值解,其他各曲线则依据一次近似解式(33)得到。可以看出,当β取常值-1/7 250时,N1/2同样会在90多千米高度出现极小值,这足以说明N1/2在90多千米高度出现极小值与β的绝对值在该高度有极大值不相关或相关性很低。 为了进一步确定高超声速沉浮阻尼特性变化规律的主要影响因素,图8给出了依据一次近似解式(33)得到的与图7中曲线相对应的沉浮运动半衰期振荡次数N1/2随轨道速度比U的变化曲线。从图中可看出每条曲线均在U≈0.707附近出现峰值,在接近U=1附近出现谷值,这与图7中的峰值和谷值相对应。 N1/2在U≈0.707附近出现峰值的原因可以由一次近似解式(33)中的主导项W5中的轨道速度比项解释,其有如下关系: (1-U2)U2≤[(1-U2+U2)/2]2=0.25 (46) 式中:当1-U2=U2,即U2=0.5或U≈0.707时,等号成立,可取得最大值。 N1/2在接近U=1附近出现谷值的原因可由一次近似解式(33)中的1/(1-f)项来解释。由图4可看出,当U接近于1时,沉浮修正参数f会突然由0快速趋近于1,进而使得1/(1-f)项急剧增大,从而改变之前由(1-U2)U2项主导的N1/2随U增加而递减的趋势。于是在接近U=1时N1/2出现了谷值,并且出现谷值的高度必然在f由0快速趋近于1的高度区间内。图9给出了依据式(30)得到的沉浮修正参数f随高度的变化曲线,可以看出图7中不同大气密度梯度参数下N1/2出现谷值的高度均在图9中f由0快速趋近于1的高度区间内。 图7 沉浮运动半衰期内振荡次数随高度的变化Fig.7 Cycles to half amplitude of phugoid oscillations vs altitude 图8 沉浮运动半衰期内振荡次数随轨道速度比的变化Fig.8 Cycles to half amplitude of phugoid oscillations vs the ratio of flight speed to orbital speed 图9 沉浮修正参数随高度的变化Fig.9 Phugoid correction factor vs altitude 综上分析,高超声速沉浮阻尼特性的变化规律主要由轨道速度比U和沉浮修正参数f主导,而与大气密度梯度参数β的相关性较低。其中轨道速度比U的影响关系式(1-U2)U2表征纵向升力与“离心力”的乘积,且当纵向升力与“离心力”相等,即轨道速度比U为0.707时,沉浮阻尼比取极小值;而沉浮修正参数f则对接近轨道速度时沉浮阻尼特性的急剧变化具有主导作用。 4.2 再入沉浮振荡轨迹的抑制 由前述可知高超声速滑翔再入飞行具有弱阻尼和低阻尼比的固有特性,因而当初始再入条件偏离平衡滑翔条件过多或各种不确定性过大导致预测控制误差较大时,飞行器容易产生纵向沉浮振荡,故需要设计相应的控制器进行轨迹振荡抑制。本节对抑制振荡的控制关系进行了推导。 采用以下反馈控制结构调节纵向沉浮运动阻尼比,进而对再入纵向轨迹振荡进行抑制。 Δu=Δv-FΔx (47) 式中:Δv=[Δkσ]为闭环反馈系统的控制变量;F=[kVkγkr]为反馈增益矩阵。将式(47)代入再入飞行器纵向动态方程式(11),可得闭环反馈系统状态矩阵为 (48) 对比在不同速度下单独反馈速度、航迹角、高度的根轨迹,如图10所示,可知反馈航迹角γ时具有最有效的阻尼比调节效果,且反馈增益需随速度增加而增加。进一步由图11中不同倾侧角σ下反馈航迹角γ的根轨迹图可以看出,若要系统保持在最佳阻尼比附近,反馈增益需随倾侧角增加而减小。 下面推导航迹角反馈增益的近似解析表达式。令kV=kr=0,则航迹角反馈系统的闭环特征方程可表示为 (49) 式中: (50) (51) 考虑到高超声速飞行纵向螺旋模态的根离S平面原点很近,则由式(25)和式(26)可得以下近似关系: (52) (53) 分别将式(50)和式(51)代入式(52)和式(53),并根据式(23)的推导和图2中所示出的W1为主导项的特性,可得到航迹角反馈增益近似表达式为 (54) 图10 反馈不同参数下的根轨迹图Fig.10 Root locus for different parameters feedback 图11 反馈航迹角的根轨迹图Fig.11 Root locus for flight path angle feedback 图12 再入状态量与控制量曲线图Fig.12 Reentry state parameters and control parameters curves 图13 速度-高度空间中的再入走廊和再入轨迹Fig.13 Reentry corridor and trajectories in velocity-altitude space 为了对比轨迹振荡抑制器的效果,设置初始再入条件使得基准制导律再入轨迹产生振荡,如图12和图13中虚线所示;而嵌入轨迹振荡抑制器后的仿真结果如图中实线所示,可以看出所设计的轨迹振荡抑制器在未过多增加控制负担的情况下有效抑制了再入轨迹的振荡。 1) 所推导出的高超声速再入沉浮特性近似解析解简洁直观地表明:自然频率随轨道速度比U的变化与飞行器本体参数关系不大;高超声速再入沉浮运动具有弱阻尼和低阻尼比的固有特性,且与纵向升阻比KV成反比关系,故升阻比越大的飞行器越易产生再入沉浮振荡。 2) 验证了高超声速沉浮阻尼特性随高度的变化规律的主要影响因素是轨道速度比U和所推导的沉浮修正参数f,而不是早期研究者推测的大气密度梯度参数β,其中轨道速度比的影响关系式表征纵向升力与“离心力”的乘积,且当纵向升力与“离心力”相等,即轨道速度比U为0.707时,沉浮阻尼比取极小值。 3) 建立了再入轨迹振荡抑制的闭环反馈系统近似关系,弥补了依靠经验确定参数的不足,从而进一步完善了平衡滑翔预测-校正再入制导方法。数值仿真表明,所采用的近似控制关系能够有效抑制由初始偏差等引起的再入沉浮振荡。 [1] JOHNSON W R, LU P, STACHOWIAK S J. Automated re-entry system using FNPEG: AIAA-2017-1899[R]. Reston, VA: AIAA, 2017. [2] LU P, BRUNNER C W, STACHOWIAK S J, et al. Verification of a fully numerical entry guidance algorithm: AIAA-2016-0377[R]. Reston, VA: AIAA, 2016. [3] LU P. Entry guidance: A unified method[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(3): 713-728. [4] LU P, FORBES S, BALDWIN M. Gliding guidance of high L/D hypersonic vehicles: AIAA-2013-4648[R]. Reston, VA: AIAA, 2013. [5] WEBB K, LU P. Entry guidance by onboard trajectory planning and tracking: AIAA-2016-0279[R]. Reston, VA: AIAA, 2016. [6] PUTNAM Z R, GRANT M J, KELLY J R, et al. Feasibility of guided entry for a crewed lifting body without Angle-of-Attack control[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(3): 729-740. [7] XUE S B, LU P. Constrained predictor-corrector entry guidance[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(4): 1273-1281. [8] JOSHI A, SIVAN K, AMMA S S. Predictor-corrector reentry guidance algorithm with path constraints for atmospheric entry vehicles[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(5): 1307-1318. [9] LU P. Asymptotic analysis of quasi-equilibrium glide in lifting entry flight[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(3): 662-670. [10] SHEN Z J, LU P. Onboard generation of Three-Dimensional constrained entry trajectories[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(1): 111-121. [11] SHEN Z J. On-board three-dimensional constrained entry flight trajectory generation[D]. Ames, Iowa: Iowa State University, 2002: 19-64. [12] HARPOLD J C, GRAVES C A. Shuttle entry guidance[J]. Journal of Astronautical Sciences, 1979, 37(3): 239-268. [13] 胡军, 张钊. 载人登月飞行器高速返回再入制导技术研究[J]. 控制理论与应用, 2014, 31(12): 1678-1685. HU J, ZHANG Z. A study on the reentry guidance for a manned lunar return vehicle[J]. Control Theory & Applications, 2014, 31(12): 1678-1685 (in Chinese). [14] 崔乃刚, 黄荣, 傅瑜, 等. 基于匹配渐进展开的跳跃式再入解析预测-校正制导律设计[J]. 航空学报, 2015, 36(8): 2764-2772. CUI N G, HUANG R, FU Y, et al. Design of analytical prediction-correction skip entry guidance law based on matched asymptotic expansions[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(8): 2764-2772 (in Chinese). [15] 杨勇, 张辉, 郑宏涛. 有翼高超声速再入飞行器气动设计难点问题[J]. 航空学报, 2015, 36(1): 49-57. YANG Y, ZHANG H, ZHENG H T. Difficulties in aerodynamic design problems of the winged hypersonic reentry vehicle[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 49-57 (in Chinese). [16] JORRIS T R. Common aero vehicle autonomous reentry trajectory optimization satisfying waypoint and no-fly zone constraints[D]. Wright-Patterson Air Force Base: Air University, 2007: 34-41, 89. [17] GUO J, WU X Z, TANG S J. Autonomous gliding entry guidance with geographic constraints[J]. Chinese Journal of Aeronautics, 2015, 28(5): 1343-1354. [18] ZHAO J, ZHOU R. Particle swarm optimization applied to hypersonic reentry trajectories[J]. Chinese Journal of Aeronautics, 2015, 28(3): 822-831. [19] MALL K, GRANT M J. High mass Mars exploration using slender entry vehicles: AIAA-2016-0019[R]. Reston, VA: AIAA, 2016. [20] CHEN X Q, HOU Z X, LIU J X, et al. Phugoid dynamic characteristic of hypersonic gliding vehicles[J]. Science China (Information Sciences), 2011, 54(3): 542-550. [21] 胡锦川, 陈万春. 高超声速飞行器平稳滑翔弹道设计方法[J]. 北京航空航天大学学报, 2015, 41(8): 1464-1475. HU J C, CHEN W C. Steady glide trajectory planning method for hypersonic reentry vehicle[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(8): 1464-1475 (in Chinese). [22] LANCHESTER F W. Aerodonetics[M]. London: Archibald Constable & Co.Ltd., 1908: 18-82. [23] ETKIN B. Dynamics of atmospheric flight[M]. New York: John Wiley & Sons, Inc., 1972: 323, 329-332, 337-339. [24] BAIRSTOW L. Applied aerodynamics[M]. London: Longmans, Green and Co., 1939: 447-551. [25] ASHKENAS I L, MCRUER D T. Approximate airframe transfer functions and application to single sensor control systems: WADC-TR-58-82[R]. Wright-Patterson Air Force Base: Wright Air Development Center, 1958. [26] 徐瑞娟. 对飞机纵向沉浮模态解析法的探讨[J]. 空气动力学学报, 1995, 13(4): 457-462. XU R J. An exploration on the analytical-solution for the longitudinal phugoid mode of aircraft[J]. Acta Aerodynamica Sinica, 1995, 13(4): 457-462 (in Chinese). [27] SCHEUBEL F N. Der einfluss des dichtegradienten der atmosphere auf die langsbewegung des flugzeugs[J]. Luftfahrtforschung, 1942, 19(4): 132-136. SCHEUBEL F N. The influence of the density gradient of the atmosphere on the slow motion of the airplane[J]. Aviation Research, 1942, 19(4): 132-136 (in German). [28] NEUMARK S. Longitudinal stability, speed and height: an examination of dynamic longitudinal stability in level flight, including the effects of compressibility and changes in atmospheric phenomena with height[J]. Aircraft Engineering and Aerospace Technology, 1950, 22(11): 323-334. [29] ETKIN B. Longitudinal dynamics of a lifting vehicle in orbital flight[J]. Journal of the Aerospace Sciences, 1961, 28(28): 779-788, 832. [30] LAITONE E V, CHOU Y S. Phugoid oscillations at hypersonic speeds[J]. AIAA Journal, 1965, 3(4): 732-735. [31] VINH N X, DOBRZELECKI A J. Nonlinear longitudinal dynamics of an orbital lifting vehicle[J]. Celestial Mechanics, 1971, 3(4): 427-460. [32] BERRY D T. Longitudinal long-period dynamics of aerospace craft: AIAA-1988-4358[R]. Reston, VA: AIAA, 1988. [33] MARKOPOULOS N, MEASE K D, VINH N X. Thrust law effects on the long-period modes of aerospace craft: AIAA-1989-3379[R]. Reston, VA: AIAA, 1989. [34] FERREIRA L D O. Nonlinear dynamics and stability of hypersonic reentry vehicles[D]. Michigan: University of Michigan, 1995: 9-82, 138-139. [35] REGAN F J, ANANDAKRISHNAN S M. Dynamics of atmospheric reentry[M]. Reston, VA: AIAA, 1993: 37-39, 56. [36] BETTS J T. Practical methods for optimal control using nonlinear programming[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2001: 133-134. [37] SLOTINE J E, LI W P. 应用非线性控制[M]. 程代展, 译. 北京: 机械工业出版社, 2006: 28-38. SLOTINE J E, LI W P. Applied nonlinear control[M]. CHENG D Z, translated. Beijing: China Machine Press, 2006: 28-38 (in Chinese). [38] 方振平, 陈万春, 张曙光. 航空飞行器飞行动力学[M]. 北京: 北京航空航天大学出版社, 2005: 186-204, 299. FANG Z P, CHEN W C, ZHANG S G. Aircraft flight dynamics[M]. Beijing: Beihang University Press, 2005: 186-204, 299 (in Chinese). Approximateanalyticalanalysisforphugoidcharacteristicofreentryvehiclesanditsapplications GUJie1,ZHANGShuguang1,*,YANGFan2,WANGBaoyin1 1.SchoolofTransportationScienceandEngineering,BeihangUniversity,Beijing100083,China2.ChengduAircraftDesignandResearchInstitute,Chengdu610091,China Forthehypersonicreentryvehicleadoptingtheequilibriumglide-basednumericaloranalyticalpredictor-correctorguidance,thephugoidoscillationofthereentrytrajectoryispronetobecausedatthetransitionpointfromtheinitialdescenttotheequilibriumglideorbylargepredictiondeviations.Withtheincreaseofthelift-to-dragratioofreentryvehiclesunderresearchinrecentyears,thephugoidoscillationbecomesmorenoticeabletocauseresearcherstore-examinethehypersonicphugoidcharacteristic.Aconciseapproximateanalyticalsolutionforintuitivelyexpressingthedominatefactorsforhypersonicphugoidcharacteristicofreentryvehiclesisderived,accordingtothreeorderlongitudinalflightdynamicsequationsandtheequilibriumglidecondition.Itisfoundthatthehypersonicphugoiddampingcharacteristicmainlydependsontheratioofflightspeedtoorbitalspeedandthephugoidcorrectionfactor,ratherthanontheatmosphericdensity-gradientparameterconsideredbypreviousresearchers.Acontrollerisdesignedtoeliminatethetrajectoryoscillationbyusingtheapproximaterelationderived,furtherimprovingtheequilibriumglidebasednumericaloranalyticalpredictor-correctorguidance.Effectivenessofthemethodisverifiedbythesimulationresults. reentry;hypersonicvehicle;phugoid;damping;analyticalsolution 2017-02-15;Revised2017-04-06;Accepted2017-05-09;Publishedonline2017-05-121059 URL:http://hkxb.buaa.edu.cn/CN/html/20171004.html .E-mailgnahz@buaa.edu.cn http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn 10.7527/S1000-6893.2017.121174 V212.1 A 1000-6893(2017)10-121174-12 2017-02-15;退修日期2017-04-06;录用日期2017-05-09;< class="emphasis_bold">网络出版时间 时间:2017-05-121059 http://hkxb.buaa.edu.cn/CN/html/20171004.html .E-mailgnahz@buaa.edu.cn 顾杰,张曙光,杨帆,等.再入飞行器沉浮特性近似解析及应用J.航空学报,2017,38(10):121174.GUJ,ZHANGSG,YANGF,etal.ApproximateanalyticalanalysisforphugoidcharacteristicofreentryvehiclesanditsapplicationsJ.ActaAeronauticaetAstronauticaSinica,2017,38(10):121174. (责任编辑:李明敏)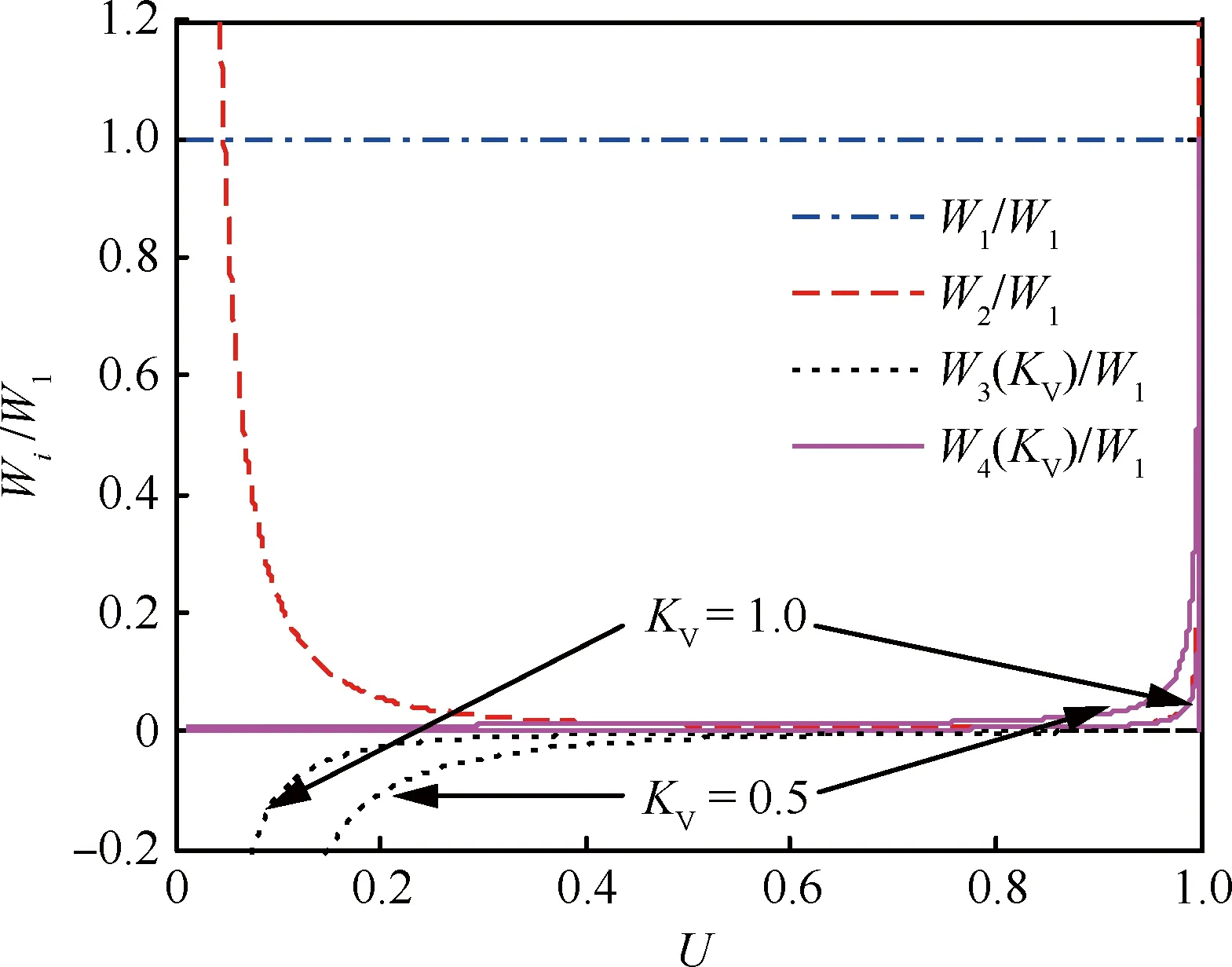

4 再入沉浮特性近似解的应用
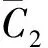
5 结 论

