用于J阻力曲线测试的载荷分离直接标定法

巫元俊，包陈，何广伟，蔡力勋

西南交通大学 力学与工程学院，成都 610031

用于J阻力曲线测试的载荷分离直接标定法

巫元俊，包陈*，何广伟，蔡力勋

西南交通大学 力学与工程学院，成都 610031

基于载荷分离原理提出了确定不同裂纹长度钝裂纹紧凑拉伸(CT)试样的载荷-位移(P-V)曲线显式表达式的方法，进而通过与尖裂纹试样的P-V曲线进行对比分析，发展了直接确定尖裂纹试样实时裂纹长度的载荷分离直接标定(LSDC)法。该方法无需在试样断面上进行任何裂纹长度的物理测量。采用Cr2Ni2MoV钢制成的CT试样验证了LSDC法的可行性和有效性。研究结果表明，LSDC法得到的J阻力曲线相比柔度法和规则化法更加合理、精确。由LSDC法还可从相同初始裂纹长度条件下的钝裂纹和尖裂纹CT试样的P-V曲线分离点得到能够真实反映材料启裂的临界断裂韧度，相比根据0.2 mm钝化偏置线交点确定的传统条件启裂韧度值更为合理，且具有更小的数据分散性。

载荷分离直接标定法；J阻力曲线；断裂韧度；Cr2Ni2MoV钢； CT试样

J阻力曲线常用于表征含裂纹结构的准静态延性裂纹扩展行为，在化工、核电、航空等关键工程结构完整性评价中发挥着重要作用，是确保相关结构服役安全的重要评价指标。裂纹准静态扩展过程中的实时裂纹长度监测是J阻力曲线测试中的关键环节。目前常用的方法包括多试样法、柔度法[1-4]、电位法[5-6]等。其中，多试样法通常需要多个同规格试样才能得到一条J阻力曲线，且无法考虑材料分散性的影响。电位法中电压与试样裂纹长度的函数关系难以统一，且在高温环境测试中的应用受到限制。柔度法中对卸载柔度的测量精度要求非常高，往往难以得到精确的裂纹长度测量结果。鉴于上述方法在J阻力曲线测试中有不同程度的限制，基于载荷分离理论[7]的规则化法[8-12]和Spb分离参数法[13]得到了一定程度的应用。包陈等[14-18]针对载荷分离方法的不足作了大量的研究，提出了修正的规则化法，并被国家标准GB/T 21143—2014[19]推荐为标准测试方法之一。然而，修正的规则化法在标定过程中一方面对标定函数作出了相关假设，另一方面要求试样在加载过程中产生足够的裂纹扩展且其载荷出现明显的下降，还要求从试样断面测得其初始及终止裂纹长度。规则化法用于裂纹扩展不明显以及小尺寸试样的J阻力曲线测试受到限制。为此，本文基于载荷分离理论提出一种直接标定(Load Separation based Direct Calibration,LSDC)法，通过对比钝裂纹与尖裂纹试样的载荷-位移(P-V)曲线求得试样实时裂纹长度，且无需在试样断面上进行裂纹长度的物理测量。采用Cr2Ni2MoV材料制成的紧凑拉伸(CT)试样对此方法的有效性进行验证。

1 材料与试验

采用具有良好淬透性和韧性的转子材料Cr2Ni2MoV开展LSDC法的可行性研究。Cr2Ni2MoV的室温力学性能为：弹性模量E=215 GPa，屈服强度σs=860 MPa ，抗拉强度σb=978 MPa，延伸率为16%，断面收缩率为50%。

试样为标准构型的台阶型紧凑拉伸(Load Line Compact Tension,LLCT)钝裂纹和尖裂纹试样构型，如图1所示，试样宽度W=50 mm，厚度B=25 mm。其中，钝裂纹试样的裂尖采用直径为2 mm的圆弧设计以确保加载过程中裂纹无扩展，初始裂纹长度a0/W=0.5，用于验证有限元模拟的准确性。对尖裂纹试样开侧槽，侧槽深度为0.1B，初始裂纹长度a0/W=0.6～0.7，共5个试样。

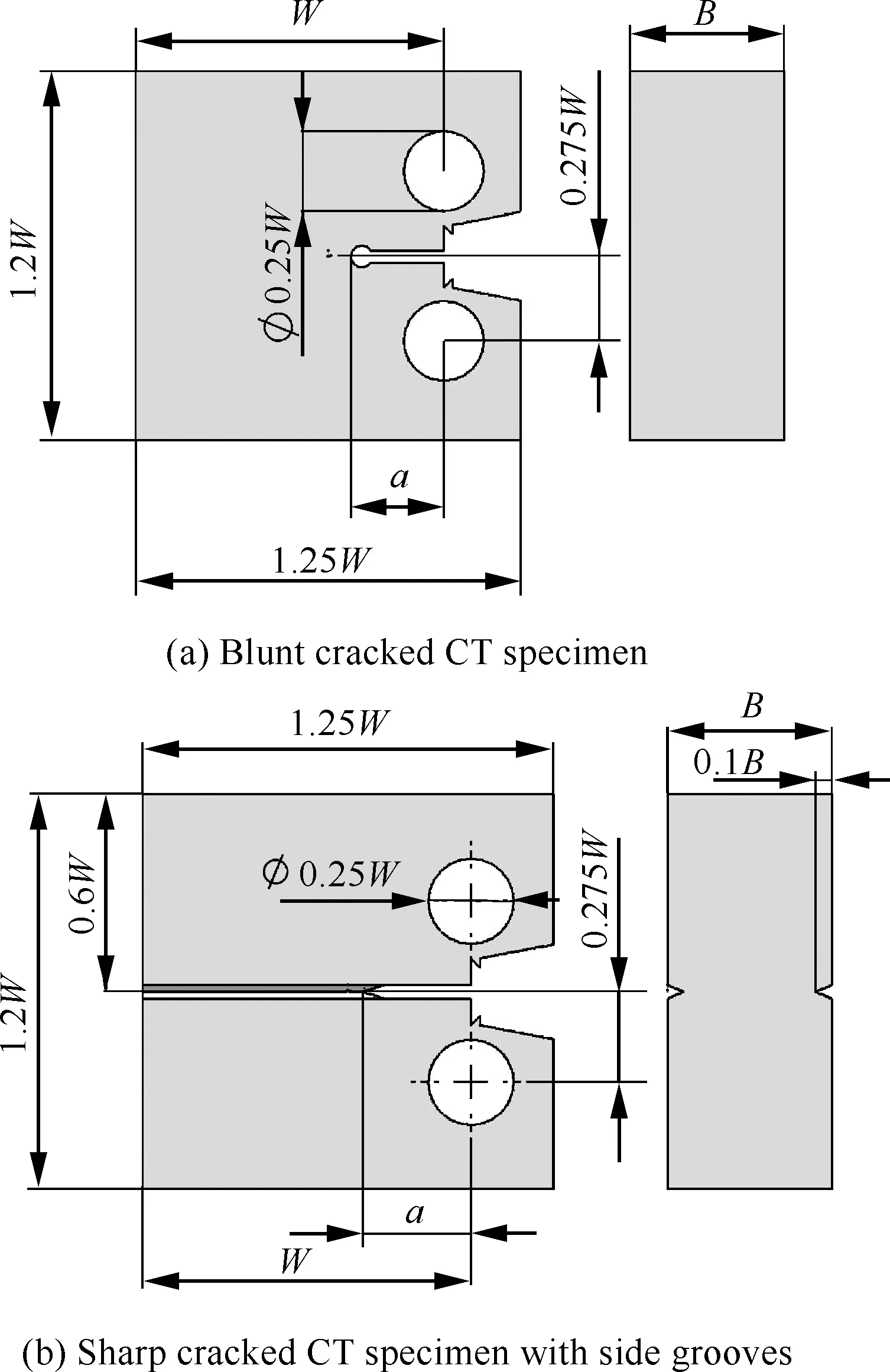
图1 钝裂纹和尖裂纹紧凑拉伸(CT)试样示意图Fig.1 Schematics diagrams of blunt and sharp cracked Compact Tension (CT) specimens

试验在MTS809 25kN电液伺服材料试验系统上完成，控制系统为TextStarII。采用MTS632.02F-20引伸计测量试样的裂纹张开位移。对钝裂纹试样进行单调加载，获取其P-V曲线。采用柔度法完成2个尖裂纹试样的J阻力曲线测试，其余3个试样采用规则化法进行测试。

2 LSDC法确定J阻力曲线

2.1 载荷分离假设

包陈等[14-15]的研究表明，CT试样的载荷P可以表示为2个相互独立的几何函数g(a/W)和变形函数h(V/W)的乘积，即

(1)

式中：Π为载荷P的无量纲量；σ0为参考屈服应力；a为裂纹长度；m为待定参数。

引入分离参数Sij来验证式(1)的假设是否成立。

(2)

式中：Πi和Πj分别为裂纹长度为ai和aj的钝裂纹试样的无量纲载荷；b为剩余韧带长度，b=W-a。显然，由于钝裂纹试样在加载过程中不产生裂纹扩展，当Sij随着位移的增加而保持恒定时，即可验证式(1)的成立。进而，参数m可从Sij与bi/W的关系中确定。

图2 试验曲线与模拟曲线的对比Fig.2 Comparison of test and simulated curves

为了验证本文所用Cr2Ni2MoV制成的CT试样满足载荷分离假设，采用有限元方法模拟钝裂纹CT试样的加载。图2给出了钝裂纹CT试样的P-V试验曲线和模拟曲线。可以看到二者完全重合，从而验证了有限元模拟的正确性。在此基础上，模拟不同裂纹长度的钝裂纹CT试样的P-V曲线，并根据式(2)处理得到分离参数Sij与V/W的关系，如图3所示。从图3中可以看到，Sij几乎不随V/W的变化而变化，从而验证了所用试样满足载荷分离假设。图4给出了Sij与bi/W的关系，并由此得到参数m的值为2.128。

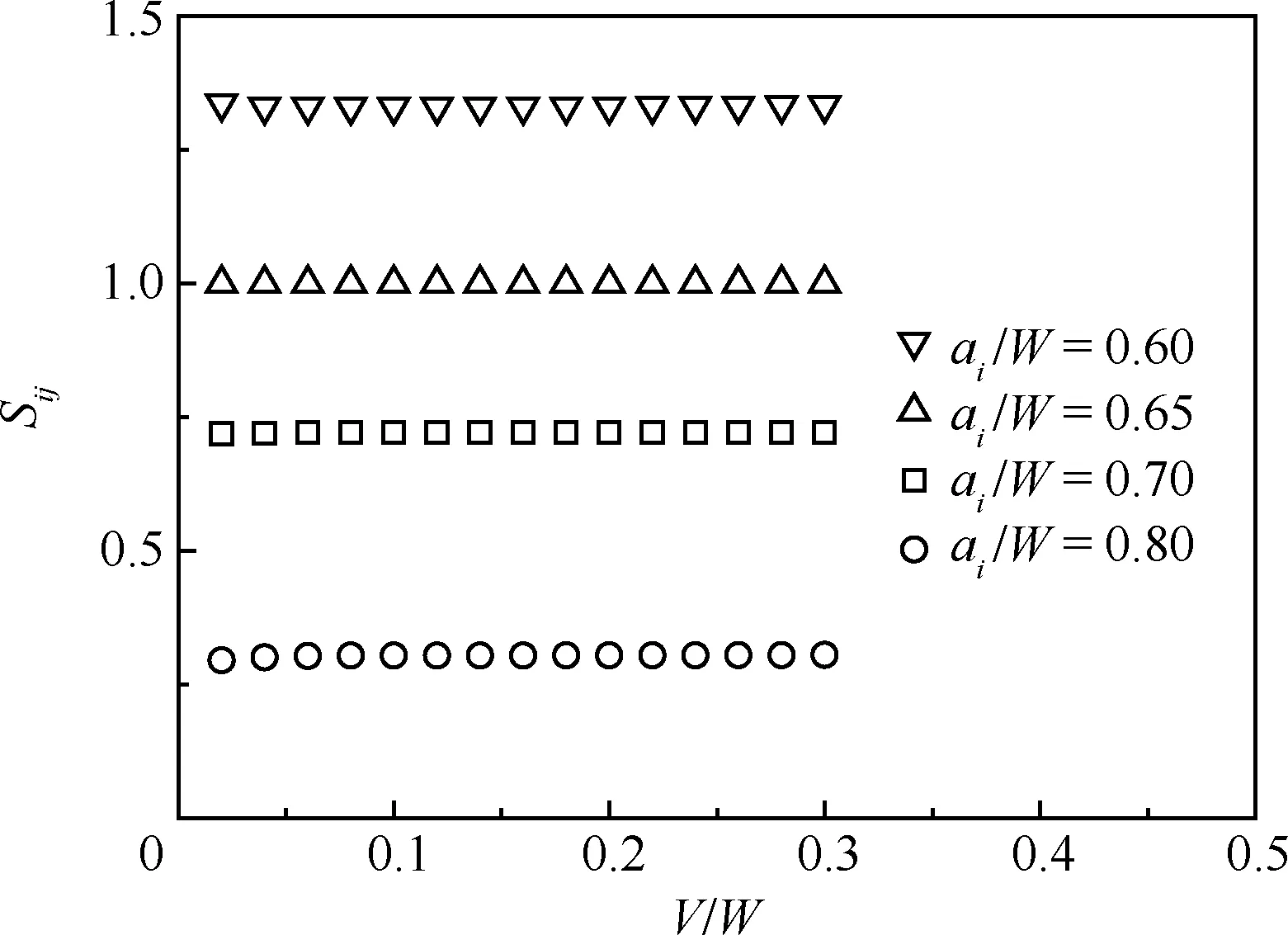
图3 Sij随V/W变化的演化规律 (aj/W=0.65)Fig.3 Evolution of Sij with change of V/W (aj/W=0.65)

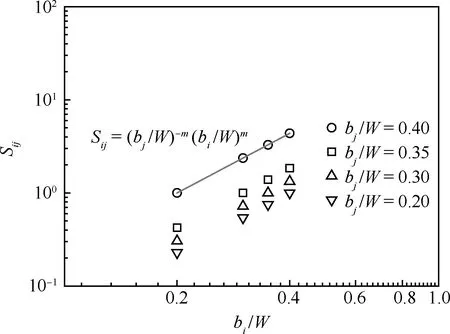
图4 Sij随bi/W变化的演化规律Fig.4 Evolution of Sij with change of bi/W

2.2 LSDC法

用几何函数g(a/W)对无量纲载荷Π作正则化处理得到ΠN为

(3)

图5给出了不同裂纹长度a对应的正则化载荷ΠN与V/W的关系曲线。可以发现，不同裂纹长度a对应的正则化载荷ΠN与V/W的关系曲线重合，这是由于式(3)中变形函数h(V/W)仅与V相关。图5中ΠN-V/W关系通过曲线回归拟合分析可以表示为

(4)

式中:P1=-0.065 32，P2=-19.544，P3=21 727.8，P4=171.961 1，P5=-954 440，P6=129 652.3，P7=63 638 182，P8=25 014.32。结合式(3)和式(4)即可得到钝裂纹CT试样P-V曲线的显式表达。

图5 ΠN随着V/W变化的演化规律Fig.5 Evolution of ΠN with change of V/W

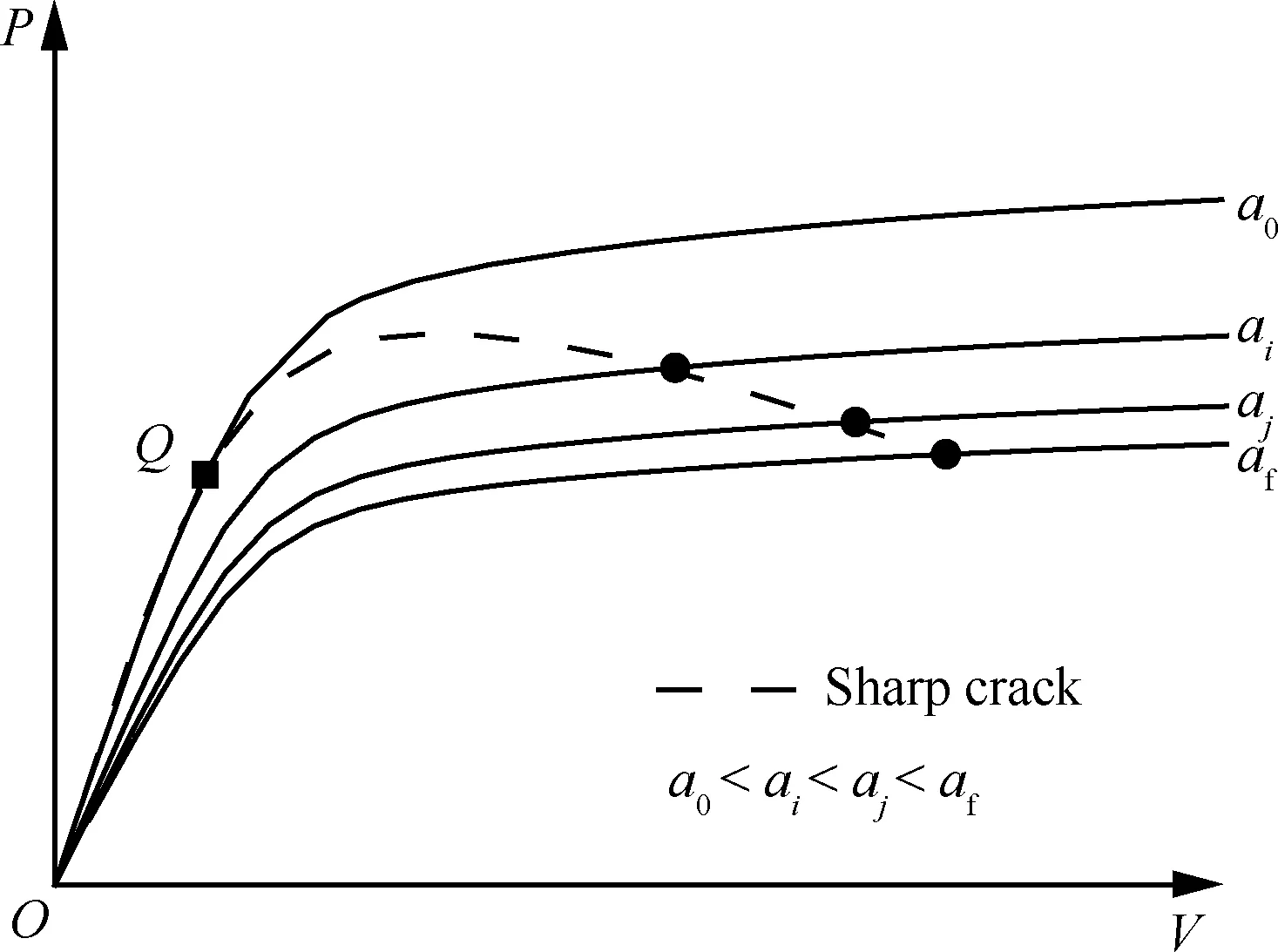
图6 LSDC法求实时裂纹长度示意图Fig.6 Schematic diagram of LSDC method for determination of instantaneous crack length

根据钝裂纹CT试样P-V曲线的显式表达可作出不同裂纹长度a对应的P-V曲线，如图6所示。图6中同时给出了初始裂纹长度为a0、终止裂纹长度为af的尖裂纹试样的P-V曲线。从图6中可以看到尖裂纹试样P-V曲线与钝裂纹P-V曲线的交点具有相同的(P，V，a)值，用尖裂纹试样的(Pi，Vi)试验点通过式(4)、式(3)和式(2)即可得到尖裂纹试样的裂纹长度ai。值得注意的是，ai可由式(4)显式求解，其求解精度与图5中ΠN-V/W关系的表达式精度直接相关，但不受表达式具体形式的影响。

从图6中还可以看出，裂纹长度为a0的钝裂纹试样的P-V曲线与尖裂纹试样的P-V曲线在变形初期完全重合，当二者分离时即代表尖裂纹试样启裂。由该分离点Q可确定尖裂纹试样的启裂载荷以及启裂韧度。通常，延性材料在启裂扩展之前会产生一定程度的裂尖钝化行为。也就是说，在分离点Q之前的初始裂纹长度应考虑钝化修正。参照包陈等[11]的研究，钝化修正的裂纹长度ab可表示为

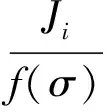
(5)

式中:Ji为对应于(Pi，Vi，a0)的J积分；f(σ)为钝化线斜率，ASTM E1820-2015[20]推荐f(σ)=2σ0，GB/T 21143—2014[19]推荐f(σ)=3.75σb。本文采用了ASTM E1820-2015推荐的钝化线斜率。

上述过程即给出了一种基于载荷分离理论通过钝裂纹试样的P-V曲线显式表达直接确定尖裂纹试样实时裂纹长度的方法，即LSDC法。由LSDC法确定实时裂纹长度后参照相关标准[19-20]即可确定J阻力曲线。

3 结果与讨论

图7给出了由不同处理方法得到的Cr2Ni2MoV钢LLCT试样的J阻力曲线。其中1#和2#试样除使用LSDC法进行处理之外，还用了柔度法以及规则化法进行处理。3#～5#试样使用了规则化法以及LSDC法进行处理。由图7可以看出，柔度法由于其所需精度较高等问题得到的J阻力曲线与LSDC法测得的J阻力曲线有一定的差别。由规则化法与LSDC法得到的J阻力曲线在靠近裂纹扩展终止点附近重合性较好，而在裂纹扩展前期由于规则化法中假定标定函数的适应性与LSDC法结果存在不同程度的差异。图7中还给出了根据图5所示的P-V曲线分离点确定的启裂韧度JQ，以及参照ASTM E1820-2015用于确定条件启裂韧度J0.2BL的0.2 mm钝化偏置线。

图8给出了根据LSDC方法测得的Cr2Ni2MoV钢5个CT试样的J阻力曲线。可以看到，不同试样的J阻力曲线在裂纹扩展量Δa大于0.1 mm时存在一定的分散性。表1列出了LSDC法求得的LLCT试样初始和终止裂纹，以及同试样断面实测裂纹长度的对比结果。表1中还给出了由LSDC法得到的J阻力曲线中确定的启裂韧度JQ和J0.2BL值。通过表1的数据可以看出，LSDC法得到的a0及af与实测结果吻合较好，最大裂纹长度测量误差不超过0.3 mm，从而验证了LSDC方法的可靠性。此外，由分离点Q确定的启裂韧度JQ值明显低于J0.2BL值，且不同试样得到的JQ值的分散性明显低于J0.2BL值的分散性。众所周知，J0.2BL是考虑裂尖钝化行为而确定启裂韧度的经验方法。根据前述讨论，LSDC法在分离点Q前已经考虑裂尖钝化行为，且点Q真实体现了裂纹启裂行为，其用于表征材料的启裂韧度相比J0.2BL值更为合理。

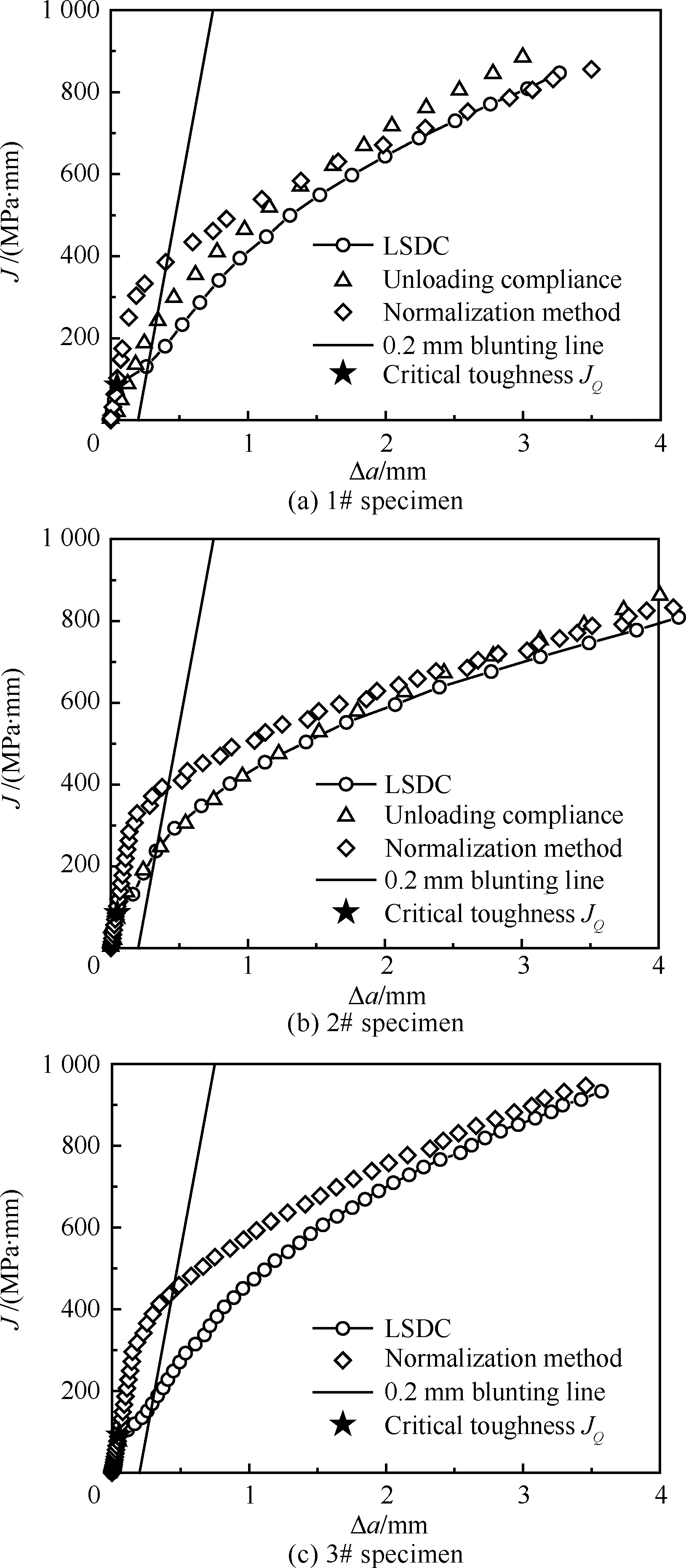
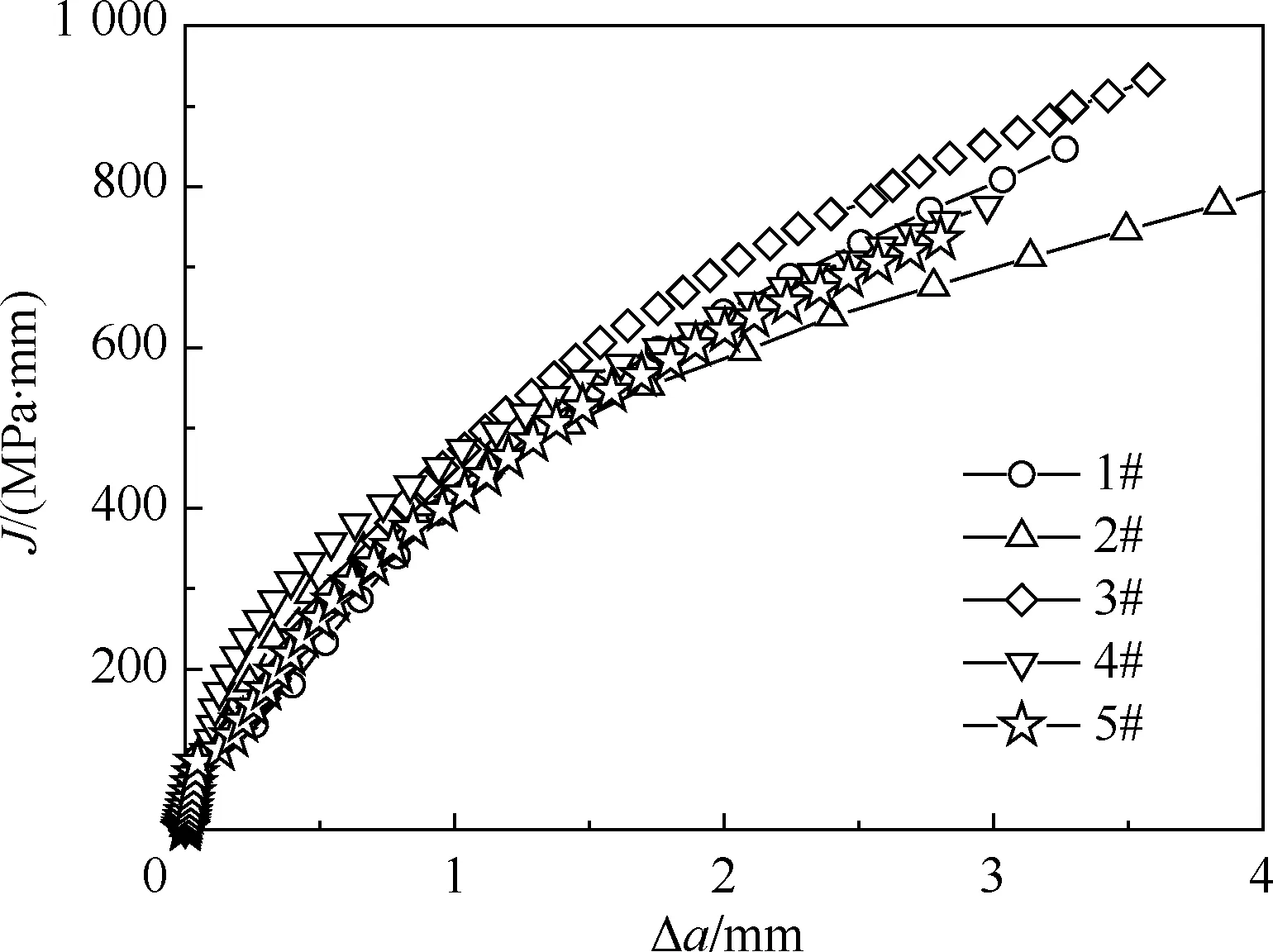
图8 不同试样通过LSDC法处理得到的J阻力曲线对比Fig.8 Comparison of J-resistance curves for different specimens resulted from LSDC method

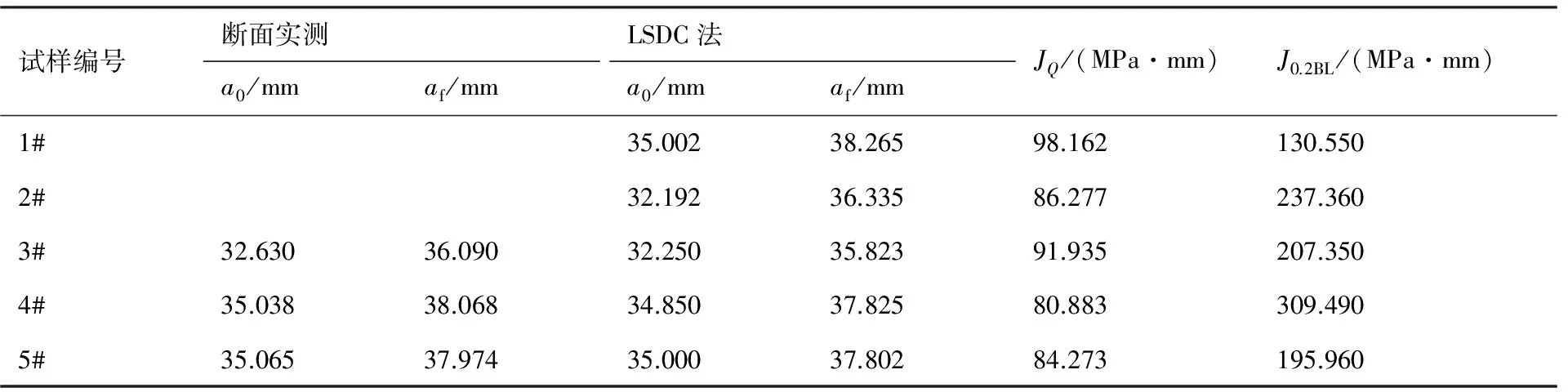
表1 LSDC法所得的裂纹长度和启裂韧度

4 结 论

1) 提出了一种用于J阻力曲线测试的LSDC方法。在该方法中，借助载荷分离原理和有限元分析可以获得不同钝裂纹长度试样的载荷-位移曲线的显式表达式，进而通过尖裂纹试样的载荷-位移试验曲线与钝裂纹试样的载荷-位移预测曲线可以方便地确定尖裂纹试样的实时裂纹长度，并进一步确定J阻力曲线。

2) 相比规则化法，LSDC法无需从试样断面上测量裂纹长度，且所预测的实时裂纹长度的精度可以得到保证。相对于柔度法，LSDC法对位移测量的精度要求相对较低，且可以避免卸载对J积分计算的影响。

3) LSDC法可以根据载荷-位移曲线的分离点确定更加合理且结果均匀的启裂韧度JQ，其结果明显低于传统标准方法得到的J0.2BL值。

[1] NEALE B K, PRIEST R H. On the unloading compliance method for crack length measurement[J]. Engineering Fracture Mechanics, 1984, 19(3): 441-448.

[2] BAO C, CAI L X, SHI K K, et al. Estimation ofJ-resistance curves for CT specimen based on unloading compliance method and CMOD data estimation ofJ-resistance curves for CT specimen based on unloading compliance method and CMOD data[J]. Journal of Testing & Evaluation, 2014, 43(3): 517-527.

[3] 蔡力勋, 包陈, 金蕾. 金属材料断裂力学柔度测试技术的问题与发展[J]. 中国测试, 2009(1): 9-18.

CAI L X, BAO C, JIN L. Compliance testing technology used for fracture properties of metallic materials: Problems and development[J]. China Measurement & Testing, 2009(1): 9-18 (in Chinese).

[4] 蔡力勋, 包陈. 金属材料延性断裂韧度测试中的柔度方法研究[J]. 航空学报, 2010, 31(10): 1974-1984.

CAI L X, BAO C. Investigation on compliance test method for ductile fracture toughness of metallic materials[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(10): 1974-1984 (in Chinese).

[5] DIETZEL W, SCHWALBE K H. Monitoring stable crack growth using a combined AC/DC potential drop technique[J]. Materialpruefung, 1986, 28(11): 368-372.

[6] BERGER C, VAHLE F. Application of the DC potential method to prediction of crack initiation[C]∥Proceedings of a CSNI Workshop on Ductile Fracture Tests Methods. Paris: OECD, 1982.

[7] ERNST H A, PARIS P C, LANDES J D. Estimations onJ-integral and tearing modulusTfrom a single specimen test record: ASTM STP 743[S]. West Conshohocken, PA: ASTM, 1981: 476-502.

[8] ZHU X K, LAM P S, CHAO Y J. Application of normalization method to fracture resistance testing for storage tank A285 carbon steel[J]. International Journal of Pressure Vessels and Piping, 2009, 86(10): 669-676.

[9] LANDES J D, ZHOU Z. Application of load separation and normalization methods for polycarbonate materials[J]. International Journal of Fracture, 1993, 63(4): 383-393.

[10] 蔡力勋, 包陈. 用于延性断裂韧性测试的载荷分离方法与应用[J]. 北京科技大学学报, 2011, 33(7): 868-875.

CAI L X, BAO C. Load separation method of deter mine the ductile fracture toughness of materials and its application[J]. Journal of University of Science and Technology Beijing, 2011, 33(7): 868-875 (in Chinese).

[11] 姚瑶, 蔡力勋, 包陈, 等 . 基于SENT试样获取材料断裂韧度的载荷分离法研究[J]. 机械工程学报, 2014, 50(10): 48-57.

YAO Y, CAI L X, BAO C, et al. Study on the load separation method of SENT specimens for fracture toughness assessment[J]. Journal of Mechanical Engineering, 2014, 50(10): 48-57(in Chinese).

[12] 但晨, 蔡力勋, 包陈, 等. 用于断裂韧度测试的C形环小试样的规则化方法与应用[J]. 机械工程学报, 2015, 51(14): 54-65.

DAN C, CAI L X, BAO C, et al. Normalization method used to determine fracture toughness with C-ring small size specimen and its application[J]. Journal of Mechanical Engineering, 2015, 51(14): 54-65 (in Chinese).

[13] BAO C, CAI L X. Estimation ofJ-resistance curve for Cr2Ni2MoV steel using the modified load separation parameterSpbmethod[J]. Zhejiang University—Science A (Applied Physics & Engineering), 2010, 11(10): 782-788.

[14] BAO C, CAI L X, HE G W, et al. Normalization method for evaluatingJ-resistance curves of small-sized CIET specimen and crack front constraints[J]. International Journal of Solids and Structures, 2016, 94-95: 60-75.

[15] BAO C, CAI L X, SHI K K, et al. Improved normalization method for ductile fracture toughness determination based on dimensionless load separation principle[J]. Acta Mechanica Solida Sinica, 2015, 28(2): 168-181.

[16] 包陈, 蔡力勋, 石凯凯. 无量纲载荷分离法在延性断裂韧性测试中的应用[J]. 固体力学学报, 2013, 34(1): 20-30.

BAO C, CAI L X, SHI K K. Application of non-dimensional load separation method in the ductile fracture toughness estimation[J]. Chinese Journal of Solid Mechanics 2013, 34(1): 20-30 (in Chinese).

[17] SHI K K, CAI L X, BAO C, et al. The dimensionless load separation method used for fracture toughness test and its application[J]. Applied Mechanics and Materials, 2012, 117-119: 460-466.

[18] 石凯凯, 蔡力勋, 包陈, 等. 断裂韧性测试中的载荷分离法及应用[J]. 中国测试, 2015, 41(1): 16-20.

SHI K K, CAI L X, BAO C, et al. Load separation method in fracture toughness test and applications[J]. China Measurement & Testing, 2015, 41(1): 16-20 (in Chinese).

[19] 中国国家标准化管理委员会. 金属材料准静态断裂韧度的统一试验方法: GB/T 21143—2014[S]. 北京：中国标准出版社，2015.

Standardization Administration of the People’s Republic of China. Metallic materials-unified method of test for determination of quasistatic fracture toughness: GB/T 21143—2014[S]. Beijing: Standards Press of China, 2015 (in Chinese).

[20] ASTM. Standard test methods for measurement of fracture toughness: ASTM E1820-2015[S]∥Annual Book of ASTM Standards: Vol.3.01.West Conshohocken, PA: ASTM, 2015.

LoadseparationbaseddirectcalibrationmethodforestimatingJ-resistancecurves

WUYuanjun,BAOChen*,HEGuangwei,CAILixun

SchoolofMechanicsandEngineering,SouthwestJiaotongUniversity,Chengdu610031,China

TheexplicitexpressionofP-VcurvesforbluntcrackedCompactTension(CT)specimenswithdifferentstationarycracklengthsisproposedbasedontheprincipleofloadseparation.Theload-displacement(P-V)curveofsharpcrackedCTspecimensiscomparedwiththatofbluntcrackedCTspecimen.TheLoadSeparationbasedDirectCalibration(LSDC)methodisdevelopedtoestimatetheinstantaneouscracklengthofthesharpcrackedCTspecimen.Anyphysicalmeasurementofthecracklengthonthefracturesurfaceofthebrokenspecimenisunnecessaryinthismethod.AgroupofCTspecimensmadeofCr2Ni2MoVsteelareusedtoverifythefeasibilityandvalidityoftheLSDCmethod.TheresultsshowthattheJ-resistancecurvesobtainedbytheLSDCmethodaremorereasonableandaccuratethanthoseobtainedbytheunloadingcompliancemethodandthenormalizationmethod.TheLSDCmethodcangetcriticaltoughnessatthepointoftheP-VcurveofsharpcrackedCTspecimenseparatingfromthatofthebluntcrackedCTspecimen,wherethetwospecimenshavethesameinitialcracklength.Thecriticaltoughnesscantrulyreflectthecrackinitiation.Comparedwithtraditionalcriticaltoughnessobtainedbytheintersectionof0.2mmbluntingoffsetlineandJ-resistancecurves,thecriticaltoughnesscorrespondingtotheseparationpointismorereasonableandhassmallerdatadispersion.

loadseparationbaseddirectcalibrationmethod;J-resistancecurves;criticaltoughness;Cr2Ni2MoVsteel;CTspecimen

2017-01-13；Revised2017-04-25；Accepted2017-05-05;Publishedonline2017-05-310942

URL：http://hkxb.buaa.edu.cn/CN/html/20171016.html

NationalNaturalScienceFoundationofChina(11472228)

.E-mailbchxx@163.com

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.221128

V215.6;O346.1+2

A

1000-6893(2017)10-221128-07

2017-01-13；退修日期2017-04-25；录用日期2017-05-05；< class="emphasis_bold">网络出版时间

时间：2017-05-310942

http://hkxb.buaa.edu.cn/CN/html/20171016.html

国家自然科学基金 (11472228)

*

.E-mailbchxx@163.com

巫元俊, 包陈, 何广伟, 等. 用于J阻力曲线测试的载荷分离直接标定法J. 航空学报，2017,38(10):221128.WUYJ,BAOC,HEGW,etal.LoadseparationbaseddirectcalibrationmethodforestimatingJ-resistancecurvesJ.ActaAeronauticaetAstronauticaSinica,2017,38(10):221128.

(责任编辑：徐晓)