基于HHC方法的旋翼噪声抑制机理及参数影响

陈丝雨，招启军，倪同兵，朱正

南京航空航天大学 直升机旋翼动力学国家级重点实验室，南京 210016

基于HHC方法的旋翼噪声抑制机理及参数影响

陈丝雨，招启军*，倪同兵，朱正

南京航空航天大学 直升机旋翼动力学国家级重点实验室，南京 210016

旋翼桨-涡干扰(BVI)噪声是旋翼气动噪声抑制的主要对象之一。其中，高阶谐波控制(HHC)是一种较为有效的噪声主动抑制方法。为探究HHC方法的降噪效果、降噪机理及参数影响规律，基于嵌套网格生成方法，采用可压雷诺Navier-Stokes方程对流场进行求解，建立了适合于模拟旋翼桨-涡干扰流场的计算流体力学(CFD)数值方法。在流场CFD分析的基础上，采用FW-H(Ffowcs Williams-Hawking)方程预测桨-涡干扰状态下的旋翼噪声，通过对施加高阶谐波控制后的BO-105模型旋翼BVI噪声进行算例验证，得到了一套可以应用于高阶谐波控制下旋翼BVI噪声估算的CFD/FW-H方法。通过对不同HHC方案的数值模拟，发现在直升机斜下降状态下，施加高阶谐波控制后的旋翼BVI噪声能够降低多达4～7 dB。进一步，细致分析了HHC方案的控制频率、输入相位以及输入幅值3个参数对旋翼BVI噪声抑制效果的影响，得到了相关参数的影响规律。并且，基于输入幅值对HHC降噪效果的影响规律，对高阶谐波控制方法的降噪机理做出了进一步的说明。

旋翼BVI噪声；RANS方程；FW-H方程；高阶谐波控制；参数分析；降噪机理

旋翼桨-涡干扰(Blade-Vortex Interaction,BVI)是由于旋转的后行桨叶与前行桨叶桨尖涡相遇碰撞而产生的直升机旋翼所特有的干扰现象。桨-涡干扰现象一旦发生，随之就会引起强烈的旋翼BVI噪声。该噪声不仅仅具备中低频噪声在大气中传播远、难衰减的特点，而且具有较强的辐射特性，会给周围环境带来一定的负面影响[1]。因此，旋翼桨-涡干扰噪声已经逐渐成为限制直升机发展的重要因素。

基于BVI噪声的产生机理，学者们提出了高阶谐波控制(Higher Harmonic Control,HHC)这一主动降噪方法，即通过降低涡强、增加桨-涡相遇距离以及改变桨-涡干扰夹角等措施来实现旋翼降噪的目的。1986年，Hardin和Lamkin[2]建立了旋翼BVI噪声的参数影响模型，指出HHC技术在旋翼BVI噪声主动抑制方面可能具备的突出潜力和应用前景。随后，NASA Langley研究中心[3]以及德国宇航局[4]各自开展了风洞试验，以进一步探究高阶谐波控制对旋翼BVI噪声的影响。通过对不同的HHC方案进行测试，充分证实了HHC方法在旋翼降噪方面具备的能力。并且发现，在直升机斜下降状态下，通过施加适当的HHC控制，能够使旋翼BVI噪声降低多达5～6 dB。同时，Beaumier等[5]对高阶谐波控制下的BO-105旋翼BVI噪声进行了预测，并提出了通过改变高阶谐波控制的输入项可能会更大程度上降低旋翼BVI噪声的设想。2001年，美国军方联合NASA Lang-ley研究中心、德国及法国宇航局，对BO-105模型旋翼进行了噪声抑制试验[6]。该试验对高阶谐波控制方法在旋翼降噪方面的潜力进行了全面的评估，并且验证了采用数值方法对施加控制后的旋翼BVI噪声进行预测的可行性。

在国内，史勇杰等[7]基于CFD方法在旋翼BVI噪声的估算及特性分析方面开展了相关研究，但尚未涉及噪声的主动控制。在旋翼噪声主动抑制方面，国内研究较少。冯剑波等[8]采用自由尾迹模型分析了HHC方法对旋翼BVI噪声的影响规律，通过依次对幅值和相位扫略，获得了HHC控制的较优方案和较劣方案。但由于自由尾迹法无法准确计算桨叶表面载荷，导致很难精确估算旋翼BVI噪声特性，这会对HHC降噪效果评估及参数影响分析的结果产生一定的干扰影响。

最近几年，学者们在高阶谐波控制的发生装置方面做了一些研究[9]，但更多的关注重点已经被转移到了单片桨叶控制(Individual Blade Control,IBC)上。而IBC虽然具有操纵自由等优点，但其系统结构复杂、操纵困难、重量和花费较大。HHC与之相比，具有结构简单、重量轻、可靠度高、易于操作及实现等优点[10]。因此，HHC是一种既具有理论意义，同时具备较高工程价值的主动降噪方法，值得深入研究。尽管国外很早就已提出将HHC应用于旋翼噪声抑制研究，并且相关工作已开展多年，但国外仅有的与HHC相关的风洞试验都存在着无法避免的局限性，比如在麦克风布置数量以及HHC方案变化等方面都受到限制。而已有的数值模拟又大多局限于对试验结果的验证，缺少参数影响分析及噪声抑制机理的深入研究。

因此，为了客观反映HHC方法对旋翼BVI噪声的抑制效果，需要结合较为精确的CFD手段对其进行更加全面的评估。此外，HHC方案的输入参数对旋翼BVI噪声抑制效果的影响，以及HHC方法实现旋翼BVI噪声抑制的内在机理仍需要进一步的研究来揭示。鉴于此，本文首先建立了一套能够用于HHC控制下旋翼BVI噪声预测的数值方法，并对BO-105模型旋翼进行了算例验证。在此基础上，为避免高阶谐波控制方案中控制频率选取的局限性，选取AH-1模型旋翼作为研究对象，通过依次改变HHC方案中的控制频率、输入幅值与输入相位的方式，探究HHC方法的各输入参数对旋翼BVI噪声抑制效果的影响规律。通过对HHC方法降噪效果的参数影响规律进行分析，提出了“微小扰动假设”，从而进一步解释了高阶谐波控制能够实现旋翼BVI噪声抑制的内在机理。

1 数值计算方法

1.1 嵌套网格方法

网格生成是CFD方法的基础。本文首先通过求解泊松方程来获得二维翼型各剖面的网格，然后对各剖面网格进行展向插值，得到整个桨叶的网格。为了更好地捕捉桨尖涡细节，通过采用绕翼型中弧线翻折策略，生成围绕桨叶的三维C-O型结构网格[11]。该区域流场由Navier-Stokes方程计算。

考虑到前飞情况，背景网格选取长方体的笛卡尔网格。并且，为了更好地捕捉桨尖涡信息，准确估算桨-涡干扰噪声，对旋翼桨尖涡形成及传播位置的背景网格进行了加密。

此外，本文采用了改进的“透视图”挖洞方法[12]来处理桨叶网格与背景网格之间的嵌套关系。为实现对背景网格洞边界单元的贡献单元进行快速搜寻，本文将Inverse Map方法[13]和伪贡献单元搜寻法[14]相结合，较大程度上提高了流场计算效率。图1给出了本文建立的运动嵌套网格系统示意图。

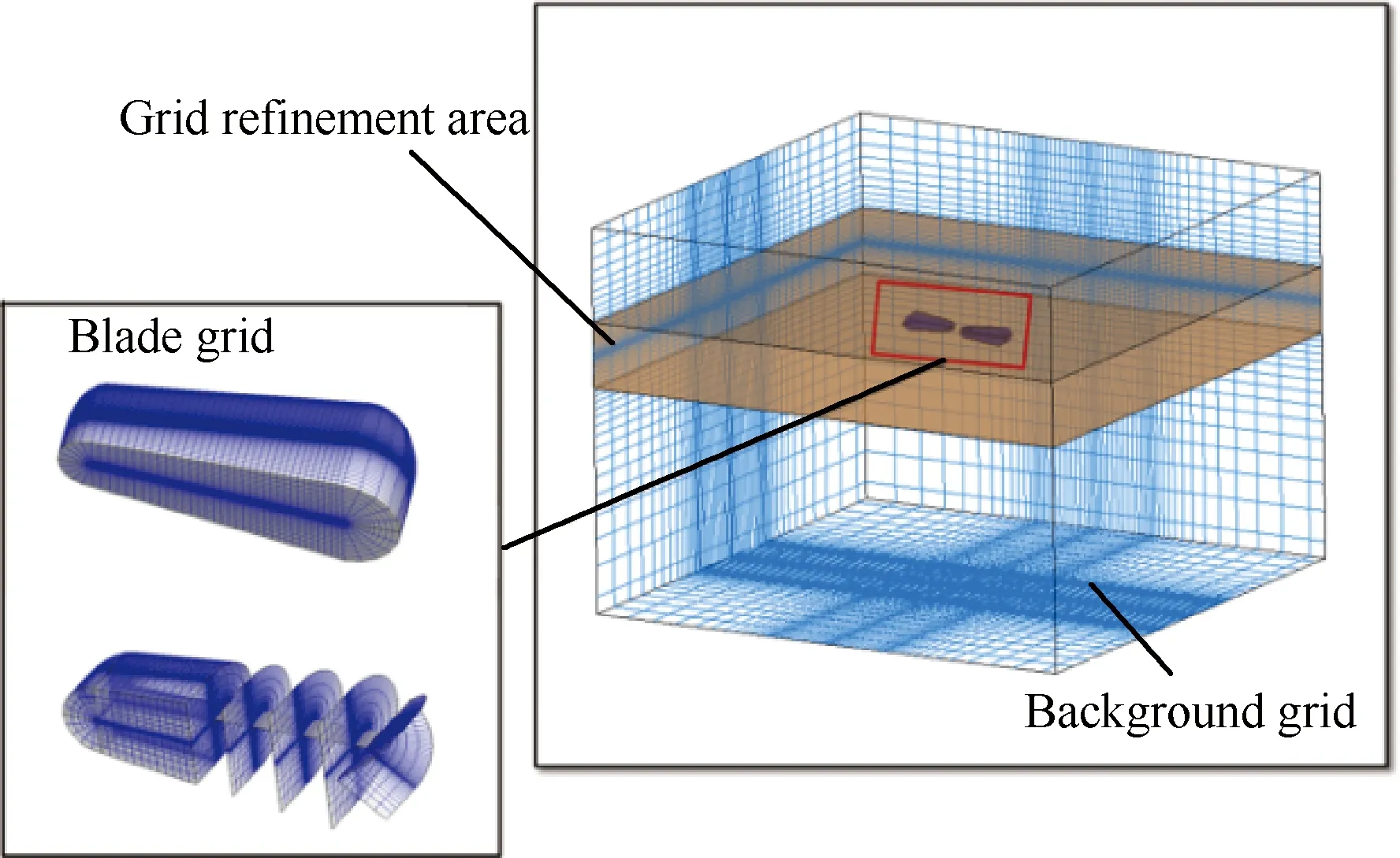
图1 运动嵌套网格系统示意图Fig.1 Sketch of moving-embedded grid system

1.2 CFD方法

前飞状态，旋翼流场同时存在可压流动(桨尖高雷诺数区域)和不可压流动(桨根低雷诺数区域)的特性，为精确捕捉旋翼非定常涡流动特性，以可压Navier-Stokes方程作为旋翼贴体网格流场求解的控制方程。考虑到旋翼运动的周期性，将坐标系建立在桨叶旋转中心，建立Navier-Stokes方程组

(1)

式中：t为时间；V为控制体体积；S为控制体表面积;W为守恒变量；F和Fv分别为对流通量和黏性通量。守恒形式变量和通量为

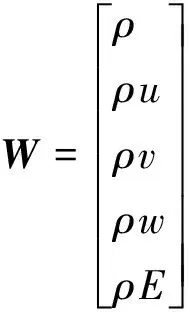
式中：(u,v,w)为气流速度；E和H分别为总能和总焓；ρ为气流密度;p为压强;τij为黏性应力张量;n=[nx,ny,nz]T为表面单位法矢;Θ=[Θx,Θy,Θz]为与黏性应力和温度导数相关的项;Vr为相对逆变速度，表达式为

Vr=V-Ve=nxu+nyv+nzw-

(nxue+nyve+nzwe)

其中，Ve=[ue,ve,we]T为牵连速度，即网格运动速度；V=[u,v,w]T为气流速度。

黏性系数计算采用S-A(Spalart-Allmaras)湍流模型，桨叶表面采用无滑移条件，物面处气流与桨叶运动的相对速度为零。远场采用无反射边界条件，即扰动波不会反射回流场。对一般亚声速问题，有Riemann不变量

式中：下标∞和e分别表示来流值和内场值；γ为比热比。因而有边界上的法向速度Vn和声速c，即

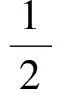
根据法向速度的符号(当Vn<0为入流边界，Vn>0为出流边界)，可从来流值或内场值中分别得到上边界的熵s′和切向速度Vt，具体为

1) 亚声速入流边界

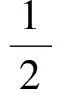
2) 亚声速出流边界

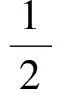
3) 超声速入流边界

ρ=ρ∞,V=V∞,p=p∞

4) 超声速出流边界

ρ=ρe,V=Ve,p=pe

根据边界上的变量值可以算出边界上的速度、密度和压力，进一步可求出边界上的守恒变量值。

为了提高流场求解的效率，本文的时间推进方法采用隐式LU-SGS(Lower-Upper Symmetric Gauss-Seidel)格式。空间离散采用有限体积法，对于交界面上的对流通量，采用ROE-MUSCL(ROE-Monotone Upwind-centered Scheme for Conservation Laws)格式[15-16]计算无黏通量和网格面上的流动变量。与二阶中心差分格式相比，可有效地减少由于截断误差和人工黏性导致的桨叶尾迹数值耗散，提高数值计算精度。

1.3 噪声计算方法

在旋翼BVI噪声预测方面，采用由Farassat给出的FW-H(Ffowcs Williams-Hawking)[15-17]方程时域解——Farassat1A公式[17]。由于BVI噪声通常发生在直升机低速斜下降的情况下，其主要成分是载荷噪声。相比其他噪声计算方法，该方法的声源积分面选在桨叶表面，能够更加精准地从流场中提取桨叶表面载荷信息。因此，采用FW-H方程对旋翼BVI噪声进行估算是较为合理的，并且能够保证较好的计算精度。Farassat 1A公式为

(2)

为提高噪声计算精度，本文采用旋转积分面[18]，直接从桨叶表面的网格上提取流场信息，避免插值引入额外的误差。

1.4 BVI噪声算例验证

直升机斜下降飞行是产生桨-涡干扰噪声的最典型状态。本节以AH-1/OLS试验旋翼典型桨-涡干扰状态为算例，通过比较桨叶表面的载荷分布和不同观察位置的声压时间历程，来验证本文给出的旋翼BVI噪声估算方法的有效性。图2给出了桨叶不同剖面(r/R=0.6、0.91)在不同方位角上的压力系数Cp的分布(1 psi=6.895 kPa)。图中，R为旋翼半径,ca为弦长,x为轴向位置。观察发现，计算值与试验值[19]总体吻合较好，说明该方法能够较好地模拟桨-涡干扰状态下的流场。

在流场模拟的基础上，为进一步验证噪声估算的精度，选取OLS(Operational Loads Survey)旋翼试验[20]中MIC3和MIC9作为观察点进行算例验证。MIC3坐标为(0，2.979R，-1.72R)，MIC9坐标为(-1.489R，2.579R，-1.72R)，其中，R为AH-1旋翼半径，旋翼中心为坐标原点，图3给出了本文噪声计算坐标系，ψ为方位角。

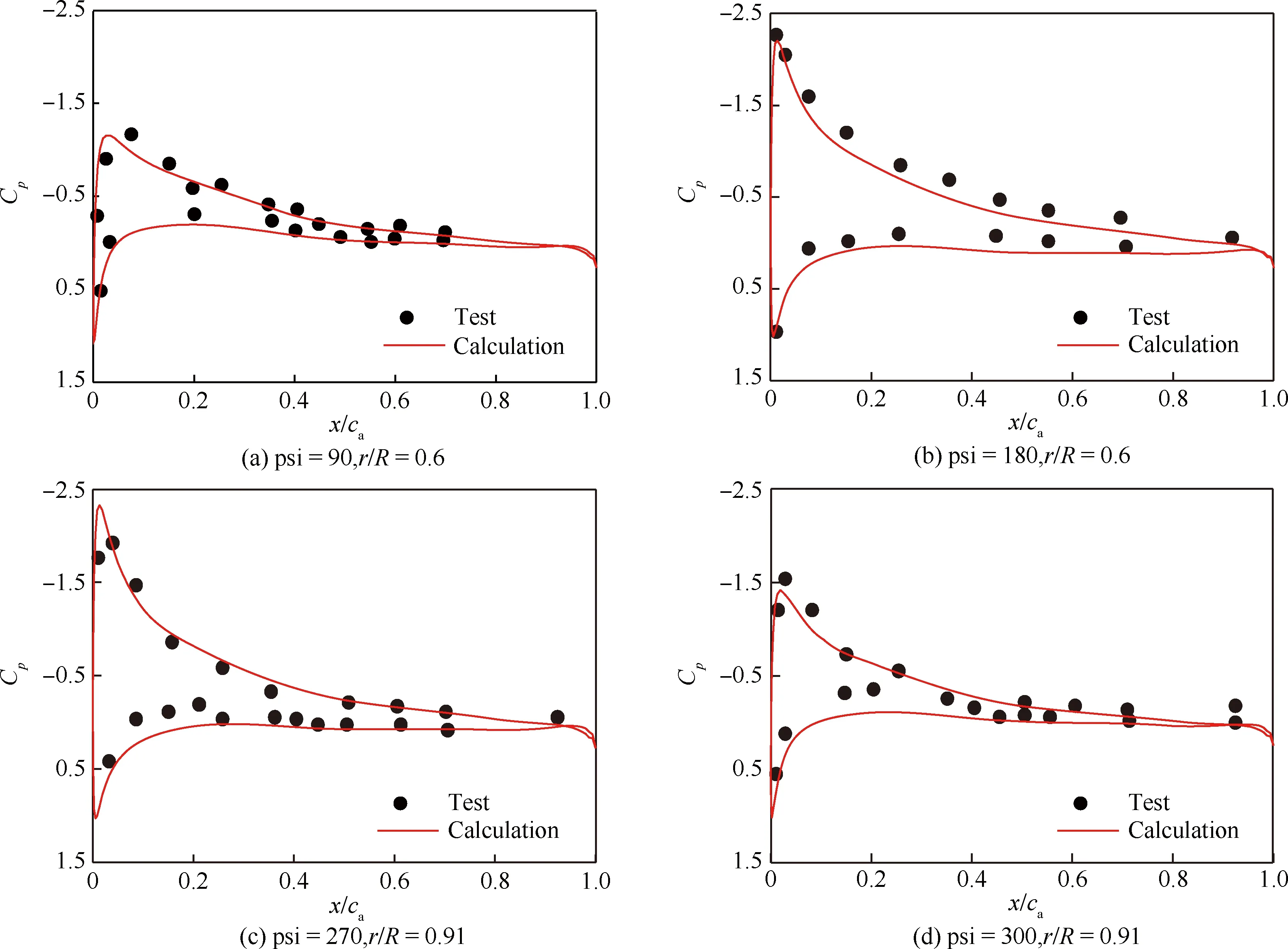
图2 桨叶剖面压力系数分布Fig.2 Distribution of pressure coefficient on blade section

图4(a)和图4(b)给出了相应声压时间历程与试验值的对比情况。从计算结果可以看出，预测得到的声压波形和峰值与试验数据拟合情况较好，这表明本文建立的数值方法是能够较好地应用于旋翼BVI噪声的预测。

图3 噪声计算坐标系Fig.3 Coordinate system for noise calculation

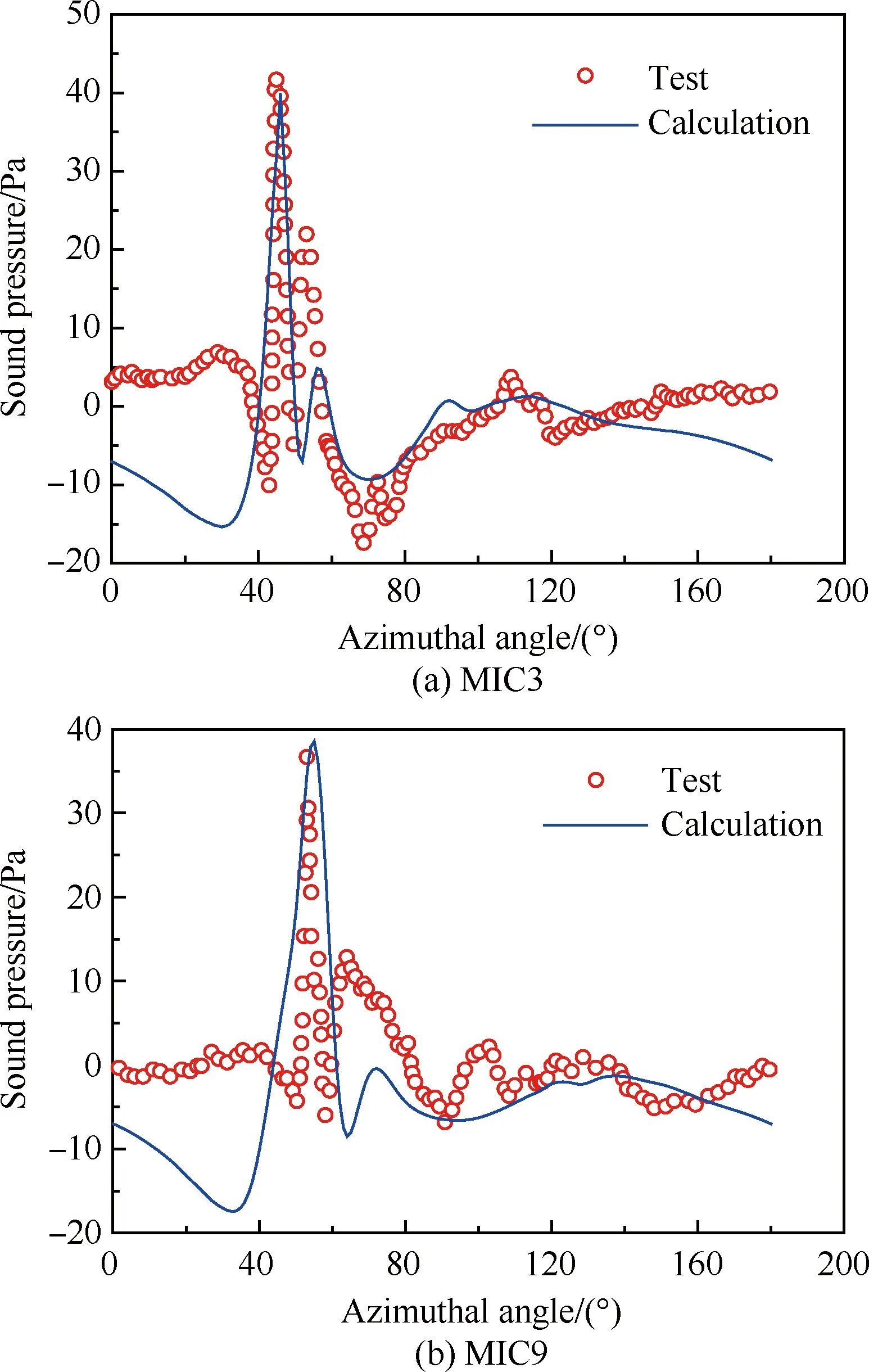
图4 声压时间历程与试验值对比Fig.4 Comparison of predicted sound pressure time histories with test data

1.5 HHC理论模型

高阶谐波控制是通过控制旋翼桨距来降低桨-涡干扰处桨叶升力/涡强度，甚至改变桨-涡干扰位置，从而实现降低桨-涡干扰强度，降低BVI噪声的目的。图5(a)和图5(b)分别给出了施加高阶谐波控制前后的桨-涡干扰示意图。

HHC方法是通过在自动倾斜器的不旋转环上施加高阶谐波操纵输入，从而实现桨距的主动控制。施加HHC控制后，旋翼桨距的变化规律[21]为

(3)

式中：NB为桨叶片数;ψi为第i片桨叶所在方位角;Ω为旋翼转速;t为时间；旋翼桨距值θ由总距θ0、横纵向周期变距θs、θc，以及高阶谐波输入项θHHC组成。其中，决定θHHC项的有3个变量：操纵输入幅值θn、操纵输入相位φC和控制频率nΩ。

以n=4,θn=-1.2°,φC=120°为例，图6给出了在施加高阶谐波控制前后，AH-1旋翼桨距随运动方位角的变化情况，图中P为频率阶数。

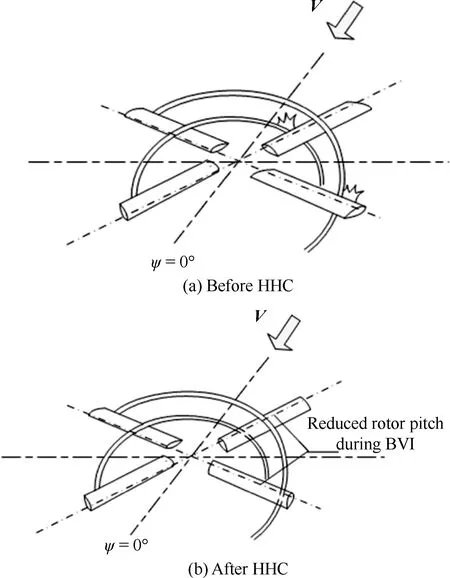
图5 桨-涡干扰示意图Fig.5 Sketch of blade vortex interaction

图6 旋翼桨距随方位角的变化Fig.6 Variation of rotor pitch with azimuthal angle

需要注意的是控制频率nΩ的选取受桨叶片数的限制[20]，n的值必须为桨叶片数的整数倍或桨叶片数整数倍加减1。对于四片桨叶的旋翼来说，HHC的控制频率被限制在3，4，5/rev(或7，8，9/rev……)的范围内，部分控制频率如2/rev、6/rev则无法应用。该局限性导致学者们逐渐将研究重点转移至控制频率不受限的单片桨叶控制。但其实对于桨叶片数不大于3的旋翼来说，HHC并不存在控制频率受桨叶片数限制的问题。如两片桨叶的旋翼，HHC的控制频率可以为1，2，3，4，5/rev……本文将以带有两片桨叶的AH-1模型旋翼为例，探究在直升机典型桨-涡干扰状态下，HHC技术对旋翼BVI噪声的抑制效果，以及HHC输入参数对抑制效果的影响，从而分析HHC的噪声主动抑制机理。

1.6 施加HHC方案下的旋翼BVI噪声计算

在建立旋翼BVI噪声估算方法的基础上，为探究高阶谐波控制对BVI噪声的影响，并对高阶谐波控制方案中的输入参数进行参数影响分析，应首先对本文的方法能否较好地应用于施加HHC方案后的旋翼BVI噪声估算进行验证。因此，本节依照现有的HHC试验，选取40%缩比的BO-105模型旋翼进行算例验证。表1给出了BO-105旋翼基本参数及试验状态参数，其他详细参数见文献[4]。

计算观察点位置坐标为(1.6,0.4,-2.4)，即试验中的麦克风位置。坐标系如图3所示噪声计算坐标系。

选取文献[4]中的2种HHC方案：4Ω,θn=-0.8°；4Ω,θn=-1.2°分别进行验证，其中相位φC变化范围为0° ～ 360°。图7给出了两种不同HHC方案施加前后，观察点处噪声声压级(Sound Pressure Level,SPL)随相位角的变化情况。观察可知，计算值与试验值具有一致的变化趋势，对于不同的HHC方案，计算值能给出与试验值变化相符的响应趋势，这说明该数值方法能够有效地评估不同HHC方案对旋翼BVI噪声的影响。而试验值与计算值在数值上略有不同，这可能是计算无法完全模拟风洞试验条件所引起的，但这并不影响HHC对旋翼BVI噪声降噪效果的评估以及参数影响分析。

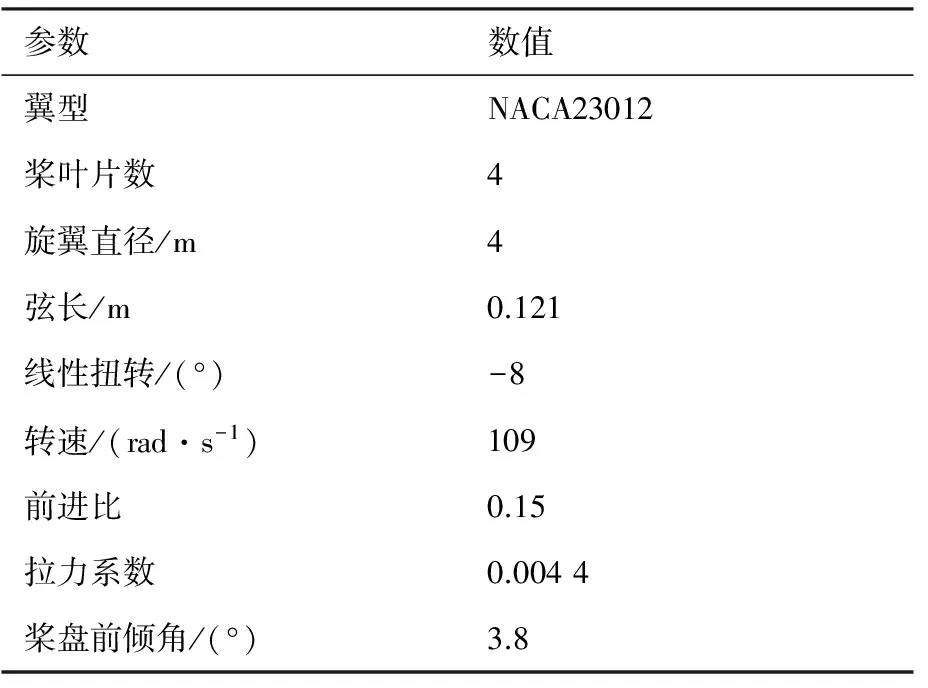
表1 BO-105旋翼基本参数及试验状态参数

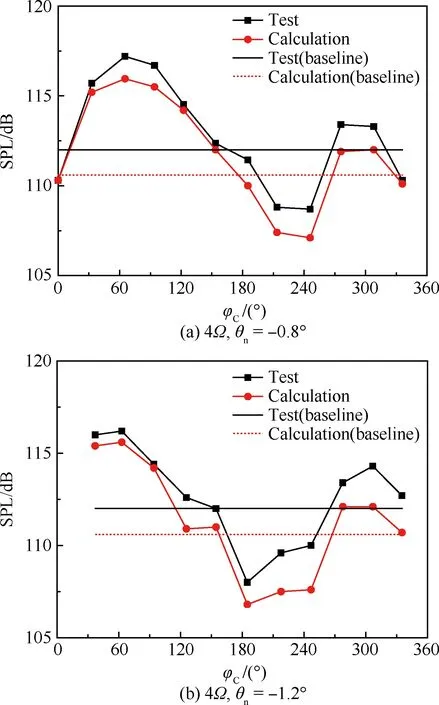
图7 HHC下BVI噪声计算值与试验值对比Fig.7 Comparison of calculated BVI noise under HHC with test data

2 高阶谐波控制的参数影响规律

为规避HHC方案中控制频率选取的局限性，选择具有两片桨叶的AH-1模型旋翼作为算例，原因已在1.5节中说明。该算例涉及的主要参数由表2给出。

已有研究表明，旋翼BVI噪声具有明显的指向性，桨盘前行侧斜下方位置的BVI噪声最强烈，对地面的影响也最为严重。针对这一现象，图8给出了桨盘前行侧斜下方8个观察点的位置示意图。8个观察点均分布在距桨毂中心3.44R的球面上，其中观察点#1，#2，#3，#4位于桨盘斜下方30°平面，#5，#6，#7，#8位于桨盘斜下方45°平面。通过对比不同HHC方案施加前后这8个观察位置的噪声总声压级大小，来探究HHC方案对旋翼BVI噪声的降噪效果，以及HHC方案中的各输入参数对旋翼BVI噪声抑制效果的影响。

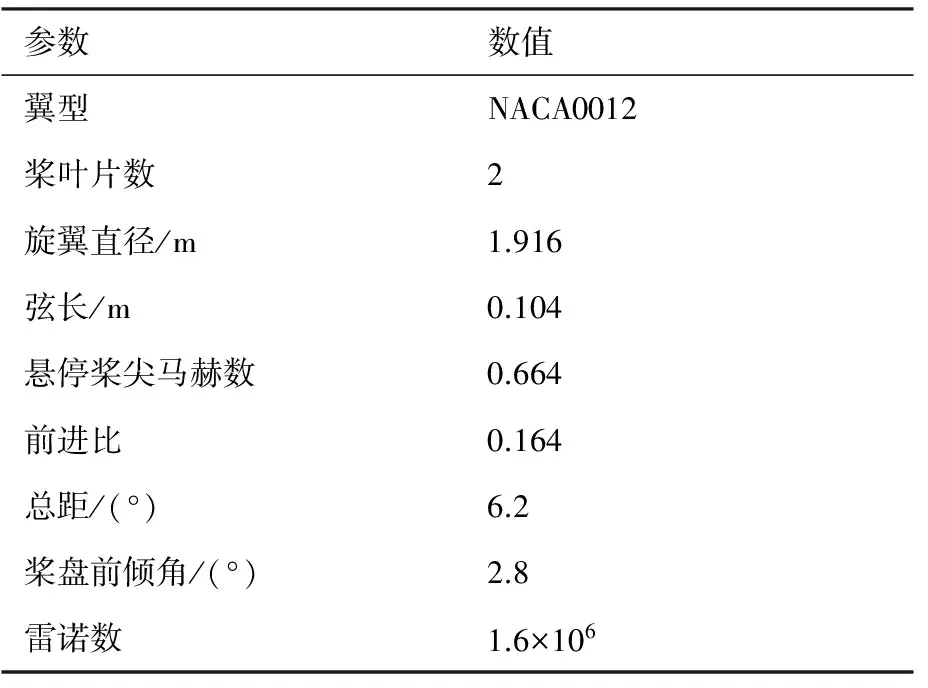
表2 AH-1旋翼基本参数及试验状态参数Table 2 Basic parameters of AH-1 rotor and test state

图8 观察点位置示意图Fig.8 Sketch of locations of observation points

2.1 控制频率对HHC降噪效果的影响

由式(3)可知，控制HHC方案的输入参数有：输入幅值θn、输入相位φC和控制频率nΩ。图9给出了输入幅值和输入相位一定的情况下，不同控制频率(3Ω、4Ω、5Ω)对8个观察位置BVI噪声的影响。横坐标代表图8中给出的8个观察点编号，纵坐标代表观察点BVI噪声的总声压级。从图中可发现，仅改变控制频率，不同的HHC方案产生的降噪效果具有相似的趋势，这与已有试验获得的结论[4]是相同的。

由1.5节可知，HHC控制频率的选取受桨叶片数的限制，而对于桨叶片数在2～5片之间的旋翼来说，4Ω的控制频率普遍适用。为尽可能考虑工程实用性，后文在进一步探究输入幅值与输入相位对旋翼BVI噪声的影响时，暂将控制频率设定为4Ω。

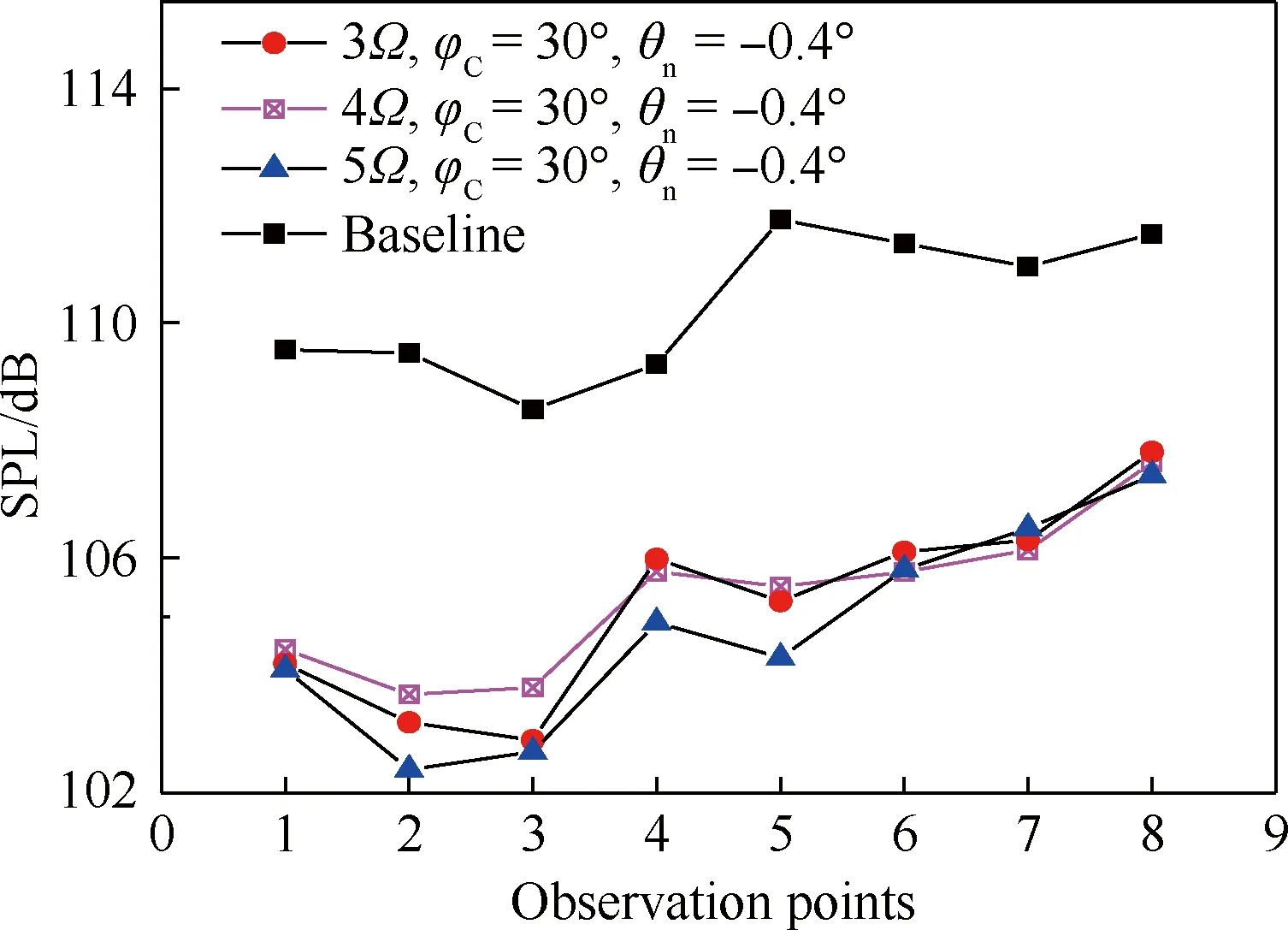
图9 不同HHC控制频率对降噪效果的影响Fig.9 Effects of different HHC frequencies on noise reduction

2.2 输入幅值对HHC降噪效果的影响

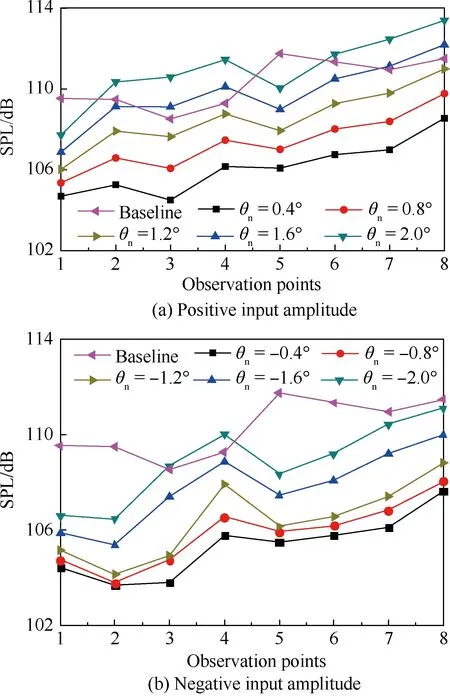
图10 BVI噪声随HHC输入幅值的变化(4Ω，φC=30°)Fig.10 Variation of BVI noise with HHC input amplitude (4Ω，φC=30°)

图10给出了控制频率和输入相位一定的情况下，BVI噪声随HHC输入幅值的变化。输入相位为30°，控制频率为4Ω，输入幅值的变化范围为(-2，-0.4)及(0.4，2)。图10(a)和图10(b)分别给出了控制频率和输入相位一定的情况下，正、负输入幅值对BVI噪声的影响。从图中可以看出，HHC方法对BVI噪声具有较好的抑制效果。对于BVI噪声辐射较强的桨盘前行侧斜下方的8个观察点，适当的HHC方案甚至能使BVI噪声降低4～7 dB。

此外，不同的输入幅值将会产生不同的降噪效果。无论是正输入幅值还是负输入幅值，随着输入幅值数值的减小，BVI噪声也随之减小，HHC方案产生的降噪效果明显提升(如：-0.4°比-2°的降噪效果更好，0.4°比2°的降噪效果好)。但通过观察可发现，不同的输入幅值仅影响噪声降低的程度，对BVI噪声的辐射指向性影响不大。

为探究输入幅值越小，HHC方案对旋翼BVI噪声产生的抑制效果是否就越好，在-0.4°～-0.02°的范围内选取了更多的数值，作为HHC方案的输入幅值，进行旋翼BVI噪声估算。图11的结果表明，HHC方案的降噪效果与其输入幅值存在相关性。即输入幅值数值越小，BVI噪声的降噪效果越明显。但当输入幅值在-0.4°～-0.05°的范围内变化时，HHC方案产生的降噪效果近乎不变。当输入幅值降低到-0.02°时，HHC方案产生的降噪效果有所削弱，这是由于幅值过小，桨叶表面的振动对流场产生的影响很微弱所致。由于受到嵌套网格方法的限制，微小的输入量变化很难在流场结果中有所体现。当输入幅值变化量小于0.03°时，流场的计算精度难以保证，同时考虑到在实际试验以及工程应用上很难达到如此小的幅值，因此本文在幅值0.02°～0.05°之间并未给出更多的结果。但由已有的结果已经可以看出，微小的输入幅值对HHC方案产生的降噪效果具有直接影响。

图11 微小输入幅值对BVI噪声的影响(4Ω，φC=30°)Fig.11 Effects of minor input amplitude on BVI noise (4Ω，φC=30°)

2.3 输入相位对HHC降噪效果的影响

为进一步探究高阶谐波控制中的输入相位对旋翼BVI噪声的影响，图12给出了控制频率(4Ω)和输入幅值(θn=-1.2°)一定的情况下，BVI噪声总声压级随输入相位的变化规律。由图可知，输入相位在30°～150°范围内，或在210°～270°范围内变化时，不同HHC方案对BVI噪声产生的降噪效果较为接近，但两者相比差距较大。这是由于控制频率为4Ω时，输入相位在一定范围内变化时，实际上只会引起桨距发生较小的相位平移，超过一个临界范围时，则会产生相位相反的结果。

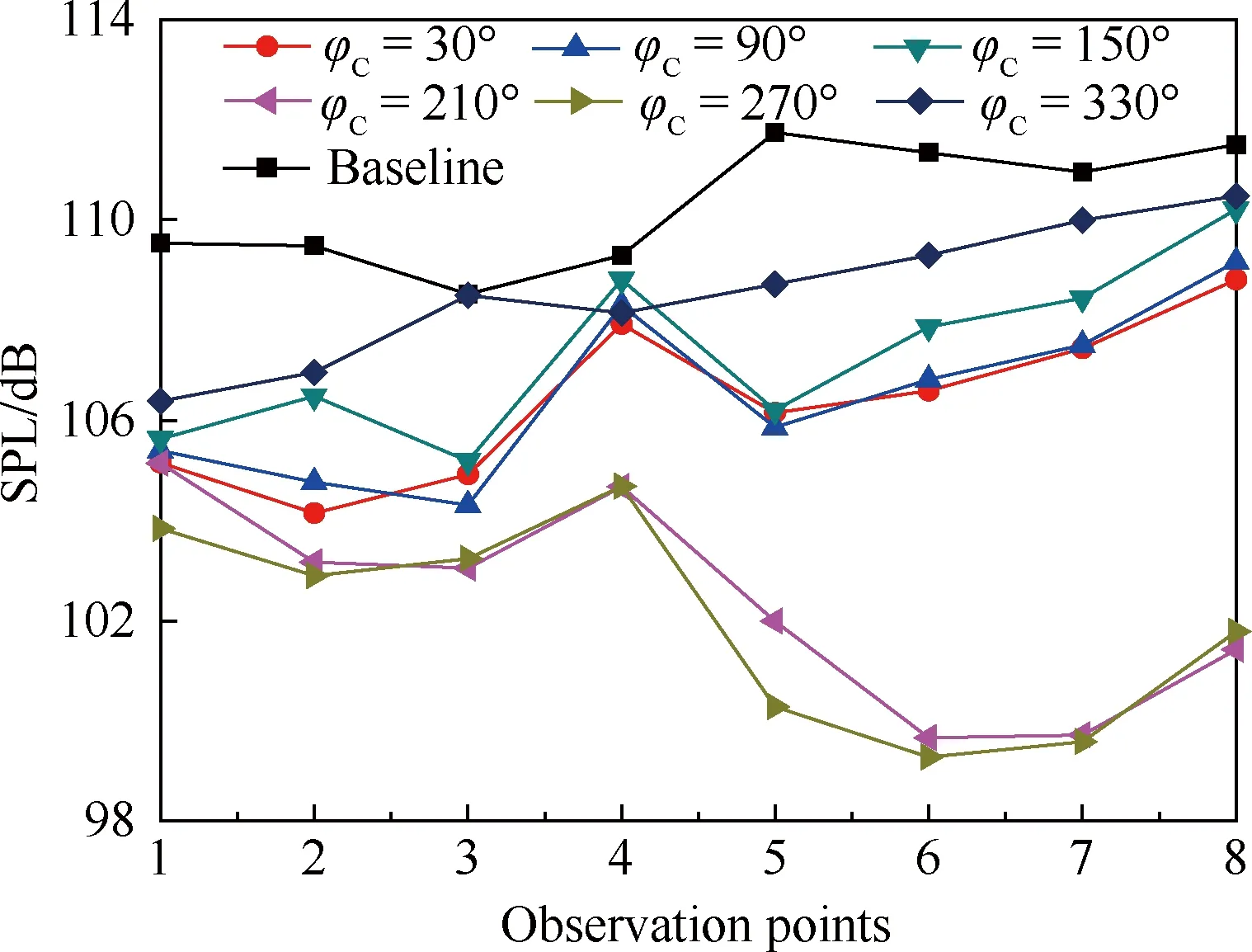
图12 输入相位对BVI噪声的影响(4Ω，θn=-1.2°)Fig.12 Effects of input phase on BVI noise (4Ω，θn=-1.2°)

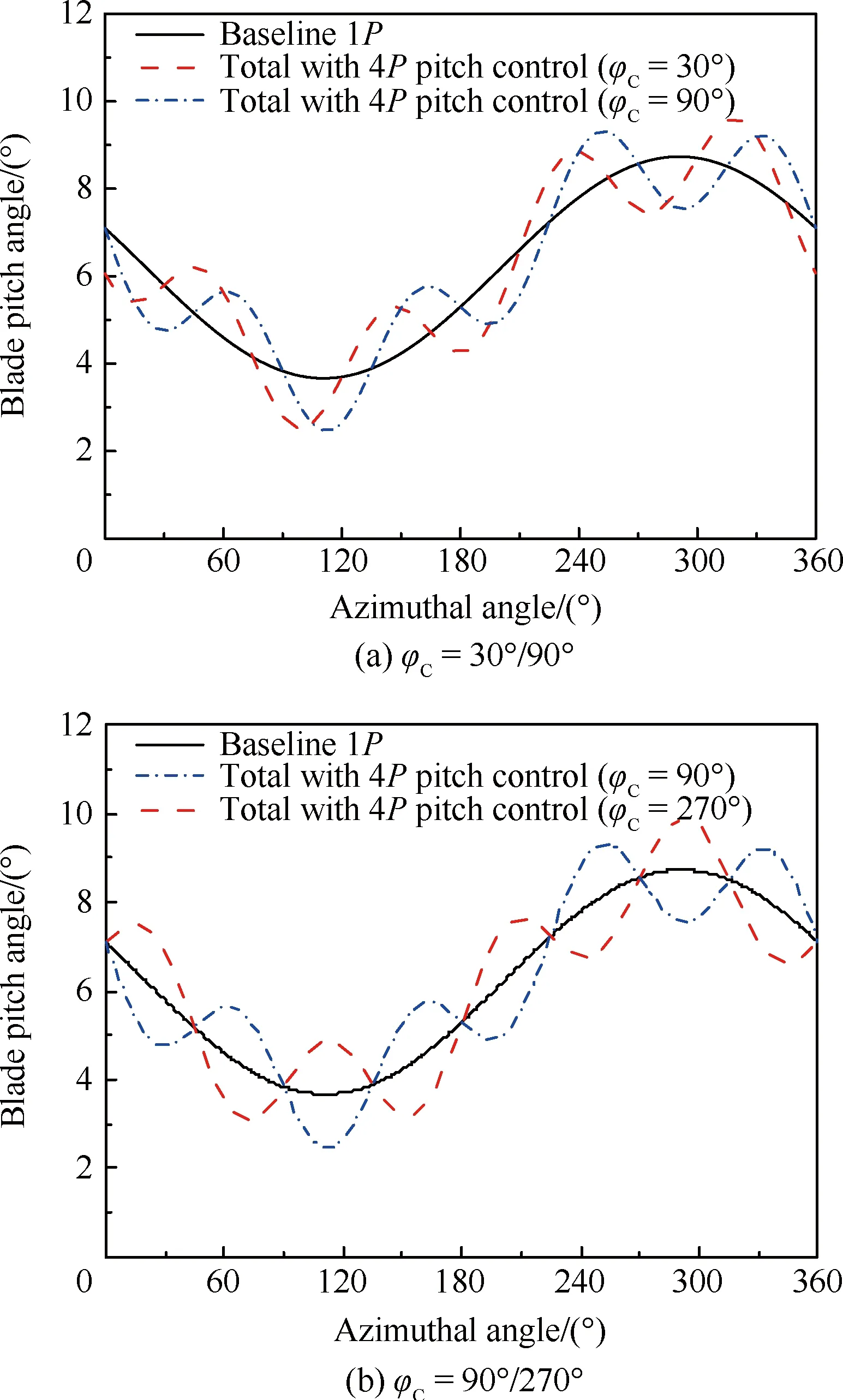
图13 不同输入相位对桨距的影响Fig.13 Effects of different input phases on rotor pitch

图13(a)给出了输入相位分别为30°和90°时，桨叶旋转一周所引起的桨距变化。对比可知，这两种输入相位引起的桨叶桨距随方位角变化的趋势相似，对于任意位置的桨叶，对应的桨距值差距不大。图13(b)给出了输入相位分别为90°和270°时，桨叶旋转一周所引起的桨距变化。结果表明，这2个输入相位引起的桨距随方位角变化的趋势完全相反，除个别方位角处桨距值不变外，大部分位置的桨叶桨距值均发生了较大的改变。

而由HHC降噪机理可知，桨距的变化直接影响了桨-涡干扰的发生。这合理地解释了输入相位在一定范围内变化时对旋翼BVI噪声产生的降噪效果相似，而超出一定变化范围时，产生的降噪效果则完全不同。

3 HHC降噪机理分析

基于2.2节中得到的输入幅值对HHC降噪效果的影响规律(即：在一定范围内，输入幅值越小，对旋翼BVI噪声的抑制效果越好)，尝试提出“微小扰动假设”：旋翼BVI噪声是源于前行桨叶桨尖涡与后行桨叶相遇发生的猛烈撞击。若通过HHC方案中的微小输入幅值给桨叶施加微小振动，则桨-涡相遇时，该微小振动会起到打散桨尖涡的作用，桨-涡碰撞的强度会在一定程度上有所缓和，涡的强度以及桨-涡干扰的发生位置也会发生改变，从而使旋翼BVI噪声显著降低。若给桨叶施加的振动幅值过大，则该振动本身会引起更大的载荷噪声，不利于总噪声的降低。

该假设可对HHC降低BVI噪声的机理起到进一步揭示的作用。为验证微小扰动假设在不同HHC方案中的普适性，本文又对输入相位为60°的情况下，不同输入幅值对BVI噪声的影响进行了估算，图14(a)、图14(b)和图14(c)分别给出了图8所示8个观察位置的厚度噪声、载荷噪声、BVI噪声总声压级的估算结果。可以看出，高阶谐波控制对旋翼厚度噪声并没有任何影响，对载荷噪声的影响规律与对BVI总噪声的影响规律相同，即HHC输入幅值越小，噪声声压级越小。当幅值减小到-0.4°时，载荷噪声不再降低。幅值过大时，载荷噪声不降反升，这是由于桨叶较大幅度的振动本身会引起较大的载荷噪声所致，这与上文提出的“微小扰动假设”相符。

图14 BVI噪声随HHC输入幅值的变化(4Ω，φC=60°)Fig.14 Variation of BVI noise with HHC input amplitude(4Ω，φC=60°)

为了能更清晰地认识当输入幅值过大时，载荷噪声以及BVI总噪声不降反升的特性，选取了图14算例中的2个典型幅值(-0.8°和-2.0°)作为输入，计算给出了这2种HHC方案下旋翼厚度噪声、载荷噪声以及BVI总噪声的声压时间历程，如图15所示。

通过对比图15中的2个HHC方案对声压信号的影响，可以发现不同的输入幅值对厚度噪声没有影响。相比输入幅值为-0.8°的情况，当输入幅值为-2°时会引起更大的载荷噪声脉冲(含BVI特征)，从而导致旋翼总噪声增大。这与图14中的结果相吻合，进一步证实了幅值过大时，载荷噪声不降反升，微小幅值更有利于BVI噪声的降低。

为进一步探究HHC降低旋翼BVI噪声的内在机理，图16给出了未施加HHC控制以及施加HHC控制后，桨叶位于90°方位角时的涡量分布图。其中，图16(a)和图16(b)分别给出了旋翼纵向截面(沿前飞方向截面)的涡量图。从图中可以看出，直升机在斜下降飞行时，采用HHC控制后，从前飞方向向后拖出的脱落涡强度减弱，且涡脱离桨叶的距离较未施加HHC控制相比更远。图16(c)、图16(d)和图16(e)、图16(f)分别给出了旋翼下方距桨盘0.1R、0.2R截面位置上，施加HHC控制前后的涡量对比图。比较可知，在施加HHC控制后， 旋翼后方及下方的脱落涡强度都呈减弱趋势，但脱落涡在空间中占据的范围有所增大。

图16 不同截面涡量分布图Fig.16 Vorticity contours of different cross sections

为更好地理解BVI噪声的产生机理，以及桨-涡干扰的发生位置，增加桨叶网格和背景网格的密度，同时降低真实时间步，以捕捉BVI状态下Cp的扰动量。图17给出了在r/R=0.91的桨叶剖面位置上，翼型上表面不同弦向位置的表面压力系数随方位角的变化趋势。η为计算点距翼型前缘点的弦向距离。从图中可以看出，距离前缘较近的区域有明显的压强扰动，距离前缘位置越远，压强扰动现象越不明显，即桨-涡干扰现象主要发生在桨叶前缘附近。这与已有文献[1]得到的结论相吻合。当桨叶运动至45°、90°方位角以及300°、360°方位角时，桨叶前缘附近产生了较强的压强扰动，这与已有研究表明的BVI发生位置相吻合。这也进一步说明了BVI噪声的产生是源于先行桨叶桨尖涡与后续桨叶相碰撞，引起后续桨叶表面的强压强扰动。

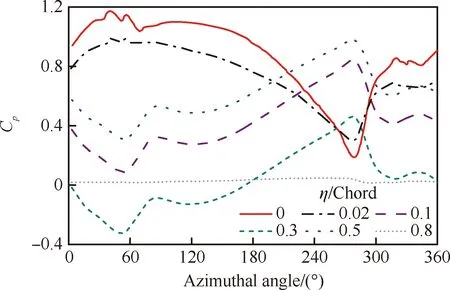
图17 不同弦向位置压力系数随方位角的变化Fig.17 Variation of distribution of pressure coefficient at different chord positions with azimuthal angle

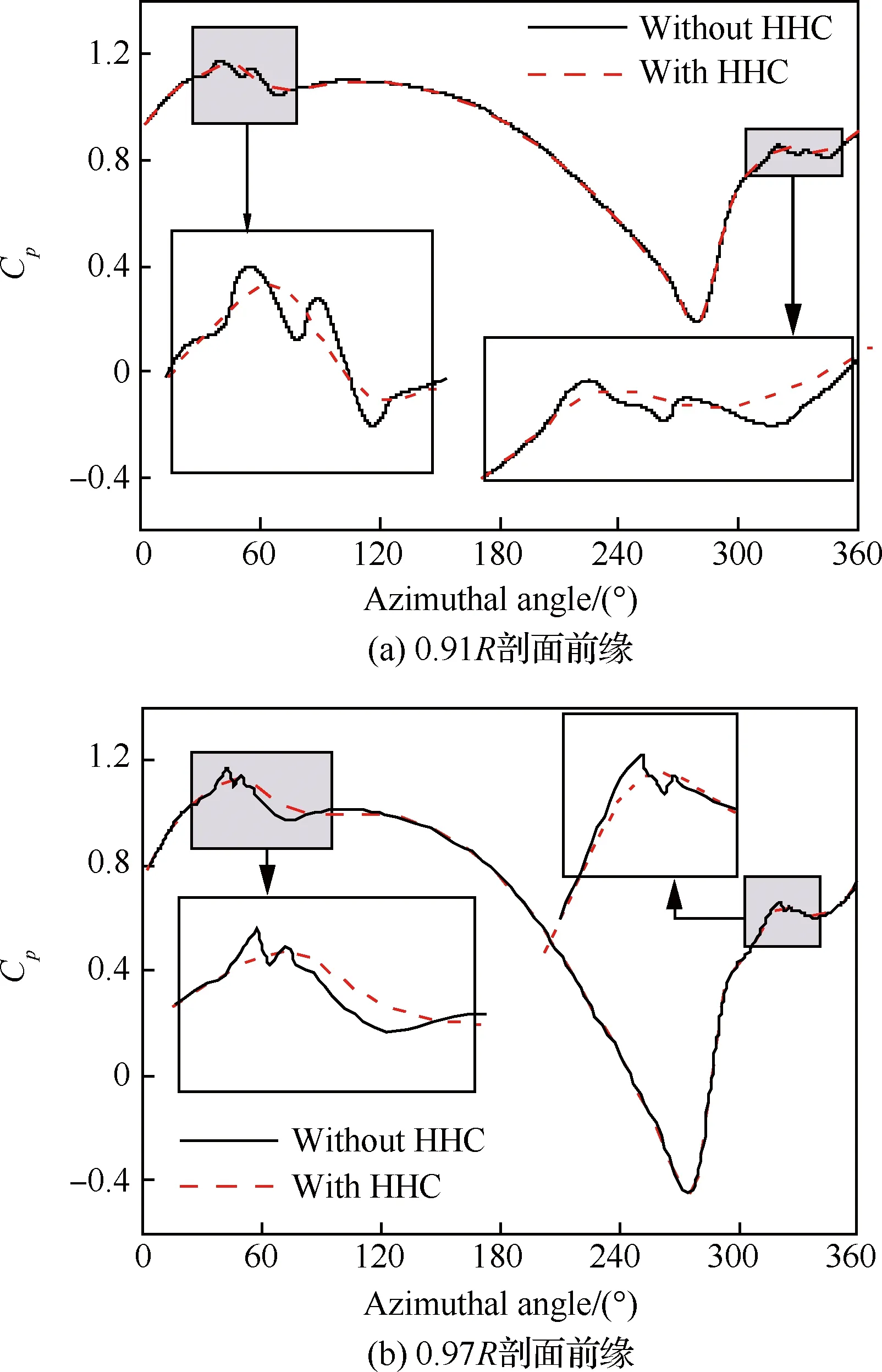
图18 桨叶前缘压力系数随方位角的变化Fig.18 Variation of distribution of pressure coefficient on blade leading-edge with azimuthal angle

明确了BVI噪声的产生机制是源于桨叶表面的压强扰动之后，本文尝试通过对比HHC施加前后桨叶表面载荷的变化，来进一步探究HHC方法的降噪机理。由于强压强扰动发生在桨叶前缘附近，故图18给出了桨叶不同剖面(r/R=0.91、0.97)前缘位置的表面压力系数随方位角的变化。通过对比HHC施加前后BVI发生区域压强扰动的变化，可以发现，通过高阶谐波控制可缓和桨叶表面的压强扰动，压力变化相对趋于平缓。结合前面对涡量强度及分布规律的分析，可以得到进一步的结论：HHC控制能够通过给予桨叶微小的高频振动，使桨叶与涡相遇时，对涡产生高频扰动，起到打散桨尖涡、降低涡强、改变桨-涡干扰发生位置的作用，从而缓和桨叶表面压强扰动，实现从源头上降低旋翼BVI噪声的目的。

4 结 论

1) 当直升机处于典型桨-涡干扰状态(斜下降状态)下，适当的HHC方案能使BVI噪声辐射较强方向上的观察点噪声声压级降低4～7 dB。

2) HHC方案中的输入幅值与降噪效果成明显相关性。对于本文中的模型旋翼，控制频率和输入相位保持不变时，输入幅值在一定变化范围内数值越小，降噪效果越好。当幅值在-0.05°～0.4°范围内变化时，降噪效果趋于不变。不同的输入幅值仅影响BVI噪声降低的程度，对BVI噪声的指向性影响不大。

3) HHC方案中的输入相位在一定范围内变化时，桨距随方位角变化趋势相似，不同HHC方案产生的降噪效果仍然相似。输入相位超出一定变化范围时，桨距随方位角变化趋势相反，不同HHC方案产生的降噪效果则截然不同。这间接地说明了HHC方法是通过控制桨距变化规律从而达到抑制旋翼BVI噪声的目的。

4) 基于输入幅值对旋翼BVI噪声的影响规律，提出微小扰动假设：若通过高阶谐波控制的微小输入幅值，给桨叶施加微小的高频扰动，则桨-涡相遇时，桨叶表面的振动能够起到打散桨尖涡的效果。涡的强度以及桨-涡干扰的发生位置会随之改变，从而缓和桨叶表面压强的扰动，使旋翼BVI噪声显著降低。若高阶谐波控制的输入幅值过大，则给桨叶施加的振动过大，这时会引起更大的载荷噪声，不利于总噪声的降低。

[1] YU Y H. Rotor blade-vortex interaction noise[J]. Progress in Aerospace Sciences, 2000, 36(2): 97-115.

[2] HARDIN J C, LAMKIN S L. Concepts for reduction of blade-vortex interaction noise[J]. Journal of Aircraft, 1986, 24(2): 120-125.

[3] BROOKS T F, BOOTH E R, JOLLY J R, et al. Reduction of blade-vortex interaction noise through higher harmonic pitch control[J]. Journal of the American Helicopter Society, 1990, 35(1): 86-91.

[4] SPLETTSTOESSER W R, SCHULTZ K J, KUBE R, et al. A higher harmonic control test in the DNW to reduce impulsive BVI noise[J]. Journal of the American Helicopter Society, 1994, 39(4): 3-13.

[5] BEAUMIER P, PRIEUR J, RAHIER G, et al. Effect of higher harmonic control on helicopter rotor blade—vortex interaction noise: Prediction and initial validation[C]∥75th Fluid Dynamics Panel Symposium on Aerodynamics and Aeroacoustics of Rotorcraft, Berlin, Germany, 1994.

[6] YU Y H, TUNG C, WALL B G V D,et al. The HART-Ⅱ test: Rotor wakes and aeroacoustics with higher-harmonic pitch control (HHC) inputs[C]∥American Helicopter Society 58th Annual Forum, 2002: 1-11.

[7] 史勇杰, 招启军, 徐国华. 旋翼桨-涡干扰气动特性计算及参数影响研究[J]. 航空学报, 2010, 31(6): 1106-1114.

SHI Y J, ZHAO Q J, XU G H. Numerical calculation and parametric study of aerodynamics of rotor blade-vortex interaction[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(6) : 1106-1114.

[8] 冯剑波, 陆洋, 徐锦法, 等. 旋翼桨-涡干扰噪声开环桨距主动控制研究[J]. 航空学报, 2014, 35(11): 2901-2909.

FENG J B, LU Y, XU J F, et al. Research on the effect of open-loop active blade-pitch control on rotor BVI noise alleviation[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(11): 2901-2909 (in Chinese).

[9] SETH P, RAMACHANDRAN A, MOHAN R. A mechanism to generate higher harmonic control for swash plates in helicopters[C]∥Asian-Australian Rotorcraft 4th Annual Forum, 2015.

[10] MALOVRH B, GANDHI F. Localized individual blade root pitch control for helicopter blade—Vortex interaction noise reduction[J]. Journal of the American Helicopter Society, 2010, 55(55): 32007-1-32007-12.

[11] 朱正, 招启军. 低HSI噪声旋翼桨尖外形优化设计方法[J]. 航空学报, 2015, 36(5): 1442-1452.

ZHU Z, ZHAO Q J. Optimization design method for rotor blade-tip shape with low HSI noise characteristics[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(5): 1442-1452 (in Chinese).

[12] SONG W P, HAN Z H, QIAO Z D. Prediction of hovering rotor noise based on Reynolds-averaged Navier-Stokes simulation[J]. Journal of Aircraft, 2007, 44(4): 1391-1394.

[13] ZHAO Q J, XU G H, ZHAO J G. New hybrid method for predicting the flowfields of helicopter rotors[J]. Journal of Aircraft, 2006, 43(2): 372-380.

[14] MEAKIN R L. A new method for establishing intergrid communication among systems of overset grids: AIAA-1991-1586[R]. Reston: AIAA, 1991.

[15] ROE P L. Approximate Riemann solvers, parameter vectors and difference schemes[J]. Journal of Computational Physics, 1981, 43(2): 357-372.

[16] VAN LEER B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov's method[J]. Journal of Computational Physics, 1979, 32(1): 101-136.

[17] DI F P. A new boundary integral formulation for the prediction of sound radiation[J]. Journal of Sound and Vibration, 1997, 202(4): 491-509.

[18] BRENTNER K S, FARASSAT F. Analytical comparison of the acoustic analogy and Kirchhoff formulation for moving surfaces[J]. AIAA Journal, 1998, 36(8): 1379-1386.

[19] CROSS J L, TU W. Tabulation of data from the tip aerodynamics and acoustics test: NACA TM-102280[R]. Washington, D.C.: NACA, 1990.

[20] YU Y H, TUNG C, GALLMAN J, et al. Aerodynamics and acoustics of rotor blade-vortex interactions[J]. Journal of Aircraft, 1995, 32(5): 970-977.

[21] KESSLER C. Active rotor control for helicopters: Motivation and survey on higher harmonic control[J]. CEAS Aeronautical Journal, 2011, 1(1): 1-20.

RotornoisereductionmechanismandparameteranalysisofHHCmethod

CHENSiyu,ZHAOQijun*,NITongbing,ZHUZheng

NationalKeyLaboratoryofScienceandTechnologyonRotorcraftAeromechanics,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China

Rotorblade-vortexinteraction(BVI)noiseisoneofthemainobjectivesofrotoraerodynamicnoisereduction.Thehigherharmoniccontrol(HHC)methodhasbeendemonstratedtobeaneffectiverotornoisereductionmethod.Toobtainnoisereductioneffects,noisereductionmechanismandparametereffectsoftheHHCmethod,aCFDmethodforsimulatingblade-vortexinteractionisestablishedbasedonmoving-embeddedgridmethodandcompressibleReynoldsaveragedNavier-Stokes(RANS)equations.BasedonthepreviousflowfieldcalculationsandFW-Hequations,anoisepredictionmethodCFD/FW-HisestablishedtopredicttheBVInoise.ThecaseofBO-105rotorwithHHCiscalculatedusingtheproposedmethod.ThecalculationresultsobtainedbysimulatingdifferentCFDcasesdemonstratethatthesoundpressurelevelsofthecasewithHHCarereducedby4-7dBduringlowspeeddescent.Theeffectsofthefrequency,phaseandtheamplitudeofHHConrotorBVInoisecontrolhavebeenanalyzed.SomeconclusionsaboutrelativeparametereffectruleshavebeenobtainedandthemechanismofHHChasbeenfurtherexplainedbasedontheinfluenceofamplitudeonnoisereductioneffectsofHHC.

rotorBVInoise;RANSequations;FW-Hequations;higherharmoniccontrol(HHC);parameteranalysis;noisereductionmechanism

2016-11-28；Revised2017-03-10；Accepted2017-05-29;Publishedonline2017-06-061912

URL：http://hkxb.buaa.edu.cn/CN/html/20171002.html

s：NationalNaturalScienceFoundationofChina(11572156);JiangsuInnovationProgramforGraduateEducation(KYLX15_0250);PriorityAcademicProgramDevelopmentofJiangsuHigherEducationInstitutions

.E-mailzhaoqijun@nuaa.edu.cn

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.121000

V211.3

A

1000-6893(2017)10-121000-14

2016-11-28；退修日期2017-03-10；录用日期2017-05-29;< class="emphasis_bold">网络出版时间

时间：2017-06-061912

http://hkxb.buaa.edu.cn/CN/html/20171002.html

国家自然科学基金(11572156)；江苏省普通高校研究生科研创新计划项目(KYLX15_0250)；江苏高校优势学科建设工程基金

*

.E-mailzhaoqijun@nuaa.edu.cn

陈丝雨，招启军，倪同兵，等．基于HHC方法的旋翼噪声抑制机理及参数影响J.航空学报，2017,38(10):121000.CHENSY,ZHAOQJ,NITB,etal.RotornoisereductionmechanismandparameteranalysisofHHCmethodJ.ActaAeronauticaetAstronauticaSinica,2017,38(10):121000.

(责任编辑：张晗)