基于蒙特卡罗方法的民用飞机故障风险评估方法

郭媛媛，孙有朝，李龙彪

南京航空航天大学 民航学院，南京 210016

基于蒙特卡罗方法的民用飞机故障风险评估方法

郭媛媛，孙有朝*，李龙彪

南京航空航天大学 民航学院，南京 210016

为提高航空安全，降低民用飞机运行过程中的故障风险水平，分别建立了单机风险和机队风险计算方法，指出单机风险计算的关键是确定部件故障分布及故障率，威布尔分布很好地描述了部件故障分布情况。针对部件故障机理，给出了部件故障的未检出概率、部件故障后果的条件概率及相应严重性后果，判定风险水平能否接受；机队故障风险在已知单机风险的基础上，取决于机队规模和当前飞行循环水平。基于机队运行数据预测故障飞机数量，获得不同参数分布、故障飞机数量和退役寿命下的机队风险水平。以某型发动机涡轮盘榫齿裂纹为例，通过蒙特卡罗方法，模拟单机及机队部件产生故障的时间，分析部件故障引起的单机风险水平和机队风险水平，基于运行数据给出民用飞机单机和机队在持续适航阶段的风险水平。

民用飞机；机队风险；单机风险；蒙特卡罗方法；累积分布函数；失效率

民用飞机作为全球航空运输的重要组成部分，保障飞行安全是对民用飞机的首要要求。随着全球航空运输需求增加，其运行安全性逐渐受到重视。随着民用飞机性能不断提高，结构愈加复杂，飞机部件在运营阶段发生故障的概率逐渐增加。因此，民用飞机风险评估方法的研究受到越来越多的关注。

国外最早对民用飞机风险进行研究[1-5]。美国联邦航空管理局于2010年发布了监控安全/分析数据(Monitor Safety-Analyze Data，MSAD)条例，对持续运行安全过程在结构和标准方面给出了指导，要求提出定量的或可发展为定量的风险分析方法。同时要求给出可计算的风险因素，包括机队风险和单机风险。其中，机队风险为在不采取任何干预措施时，机队在寿命期内潜在的未检出故障导致的后果损失。单机风险是相对于单架飞机上，机组和乘客在每个飞行单位(飞行小时或飞行循环)面临的飞机故障风险。故障模式为未检出的结构故障、失控、推进系统故障或飞行安全系统故障。分析故障风险，确定灾难性后果是否需要采取纠正措施并评估该措施能否有效降低风险。

与国外相比，国内关于民用飞机风险方面的研究起步较晚，主要在飞行安全与航空器技术的风险评估方面进行了一定的相关性研究[6-13]。采用蒙特卡罗仿真方法模拟发动机多故障发生情况，计算各故障模式的风险因子以及每次飞行风险；建立航空发动机部件故障风险仿真模型、发动机故障危险等级划分、危险系数确定和风险因子计算的方法，预测发动机故障的发生情况，评估发动机运营阶段的故障风险，制定合理的可降低风险方案，分析维修周期对风险因子的影响，给出合理的降低风险方案；借助概率统计和安全性分析方法，判断事件对单架飞机和整个机队的影响程度；提出结合极值理论与Copula模型量化评估平尾结冰条件下飞行风险概率的方法；提出一种基于Kriging和蒙特卡罗半径外重要抽样混合的结构概率风险评估方法；基于蒙特卡罗飞行仿真实验对结冰条件下人-机-环系统，构建了飞行风险发生的判定条件。随着中国民机项目的蓬勃发展，中国自主设计与生产的飞机将越来越多地获得适航认证并投入运营，但是缺乏基于MSAD提出的对持续运行安全上单机及机队风险评估的相关研究，本文对单机风险及机队风险定量计算给出了详细分析过程，并以算例进行延伸验证，动态监测机队运行状态，确保民用飞机机队运行安全。

本文基于机队运行数据，建立了单机与机队机械部件的风险评估模型，双参数威布尔分布可拟合民用飞机上各种类型的机械部件寿命数据[14]。统计表明，双参数威布尔分布对发动机故障模式分布具有很好的拟合性，在确定部件故障数据的情况下，能够很好地反映部件使用寿命与故障率之间的关系[6]。同时针对航空发动机零部件等高可靠性的产品，其故障统计通常为小样本，利用威布尔分布在处理小样本数据时优势明显[15]。本文采用威布尔分布模型预测航空发动机故障风险，指出影响风险变化趋势的关键因素，通过威布尔分布分别描述单机和机队的部件失效率及累积分布函数，以蒙特卡罗方法仿真部件故障时间。预测寿命期内飞机运行过程中飞机部件故障的风险水平及机队中故障飞机数量，确定了机队风险评估方法。以涡轮盘榫齿故障为例，建立故障未检出概率流程图，给出故障不安全后果的因果链、条件概率及相应死亡率，计算不同运行状态的单机及机队故障风险，评估在寿命期内单机风险及机队风险是否处于可接受水平，分析维修间隔及退役寿命的制定是否合理，在综合比较安全要求和经济效益的情况下，确定维修间隔、退役寿命及单机和机队的运行风险水平。

1 单机与机队风险评估模型

单机风险RI是机组和乘客在每个飞行小时/循环面临的飞机故障风险。单机风险针对单架飞机，对每个飞行循环产生故障的概率进行模拟。机队风险RF是衡量机队风险的重要指标，是机队在寿命期内由于某部件发生故障导致的运行风险。单机及机队故障风险评估流程分为3步，如图1所示。

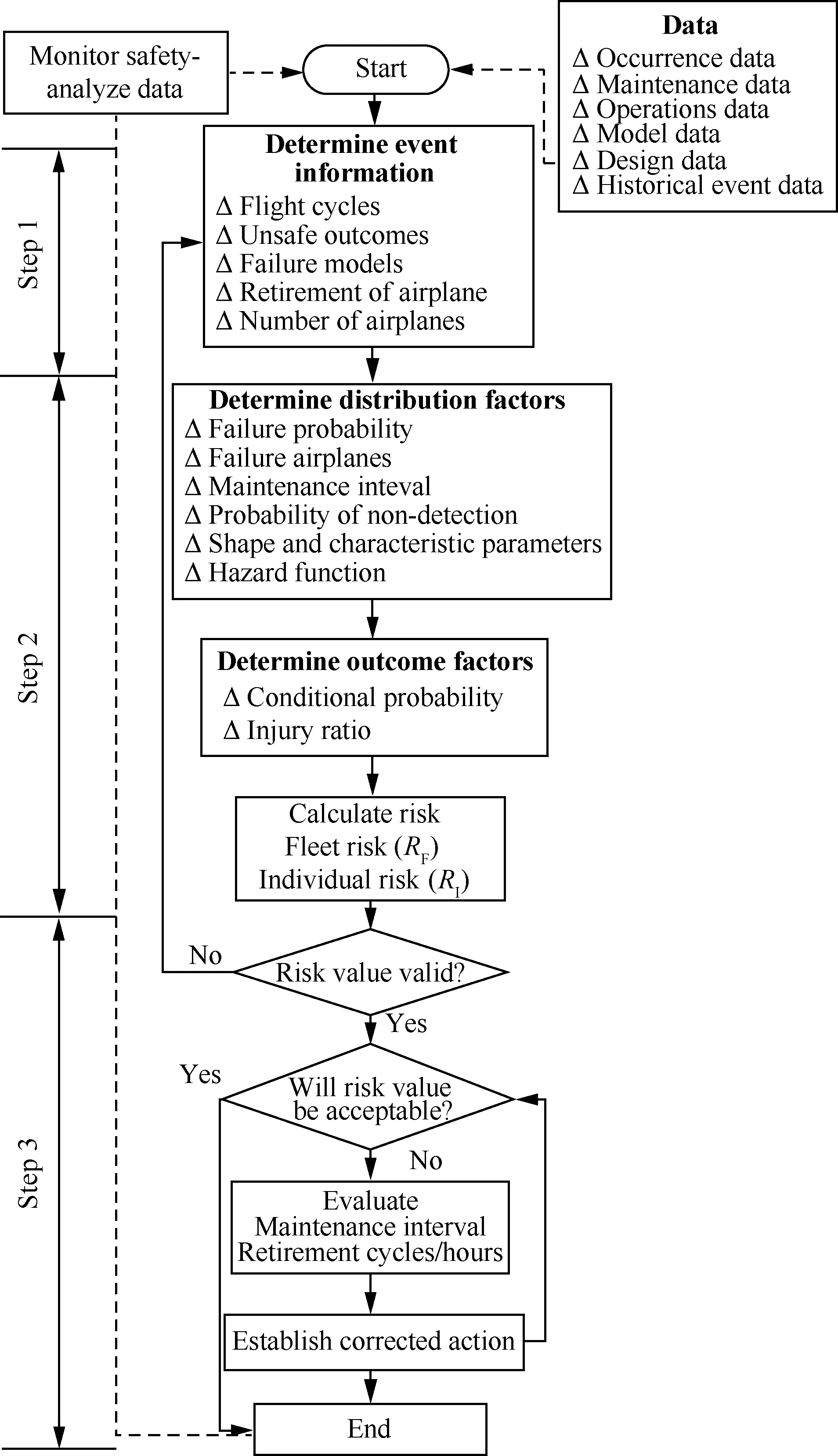
图1 机队与单机故障风险评估过程Fig.1 Processes of fleet and individual failure risk assessment

步骤1通过安全分析监控数据确定机队运行过程中存在潜在的不安全状态时，收集机队相关数据，包括当前运行数据、维修/运行数据、模型数据、设计数据和历史数据，如飞机数量、各飞机当前飞行循环、飞机退役寿命、当前已检出故障飞机数量和灾难性后果的致死率等。确定机队情况，包括研究状况、不安全后果及故障模型。确定飞机产生故障的参数，包括机队飞行循环、飞机数量和不安全状态或后果，为机队故障风险评估提供数据支持。

步骤2结合部件故障概率、故障数量、维修间隔和未检出概率，确定分布模型的形状参数、寿命参数、故障率函数和风险分布函数。通过故障因果链确定不安全后果的条件概率和致死率。计算单架飞机某部件在寿命期内的故障率和单机风险；给出预计故障飞机数，计算机队风险。

步骤3确定风险评估方法有效性，判定故障引起的机队风险是否在可接受水平。若是，无需采取措施，继续监控飞行数据[3]；若否，针对风险评估结果，分析维修间隔和退役寿命的制定是否合理，采取最优纠正措施，重新评估机队故障风险，执行步骤2。

1.1 单机风险模型

通过确定飞机部件在运行期间是否发生故障，预测在寿命期内由于该故障导致机上个体遭受致命伤害的概率[16-17]。单机风险为

RI=h(tI)μIψIfI

(1)

式中：h(tI)为部件工作到时刻tI时尚未故障，tI时刻后的下一单位时间发生故障的概率；μI为部件故障导致飞机发生不安全后果的未检出概率；ψI为飞机灾难性后果发生概率；fI为死亡率。发动机部件故障概率h(tI)为

(2)

式中：β为形状参数；η为特征寿命。查阅文献确定单架飞机部件双参数取值；收集机队运行数据，通过极大似然估计确定机队部件双参数取值。

文献[18]利用专家经验确定运输类飞机部件故障检查效果及检出概率，据此判断损伤、故障是否明显，检查手段是否有效，是否受到疲劳损伤影响等确定未检出概率μ值。如图2所示，存在5种原因使故障未检出，未检出概率越低表明部件在导致不安全后果前被检出的概率越大。

步骤1缺陷或者故障是否明显。若部件由潜在故障发展为功能故障的过程中被机组或维修检查人员容易检出，未检出概率应设为较小值μ=0.01；若否，执行步骤2。

步骤2当前执行的检查措施是否有效。若是，进一步判断潜在故障是否在检查后发展为功能故障，若是，应适当缩短该部件的维修计划间隔，并设μ=0.06；若否，执行步骤3。

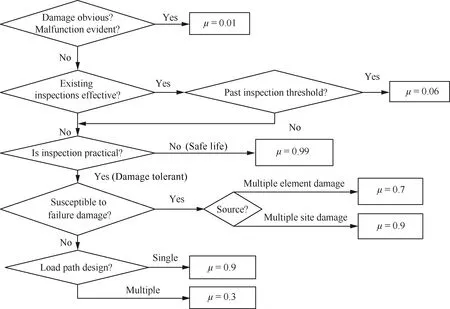
图2 确定未检出故障概率流程Fig.2 Flowchart for determining non-detection failure probability

步骤3检查是否起作用。若结构设计符合安全寿命理论，如检查脆性材料起落架结构完整度不能很好地起到检查监控作用，在发生之前很难检出，需按时移除替换，设μ=0.99；若结构设计符合损伤容限理论，如涡轮盘，对其检查起作用，执行步骤4。

步骤4是否受疲劳损伤故障影响。相邻结构部件在相似应力水平下运行并发生裂纹，若是，判断故障是由多个部件(如相邻部件，相似结构的纵梁)或是由多个点(如一个结合点的相邻紧固件)增长,这些裂纹造成灾难性后果前难以被检出[3]；若否，执行步骤5。

步骤5加载路径设计如果是单条，故障极不可能在灾难性后果发生前被检出，μ=0.9；如果是多条，未检出概率低于单条加载路径，μ=0.3。

Pai为部件发生第a种故障，发展至i状态的条件概率。给出相应部件故障因果链，如图3所示。

图3 部件故障因果链Fig.3 Causal chain of parts failure

该部件故障导致2种不安全后果。由当前故障状态顺次发展最终至不安全后果，相应死亡率为fI1、fI2。该部件发生不安全后果的风险为

1.2 机队风险模型

在机队运行过程中，存在通过无损检测未检出的故障概率，预测机队从当前到退役过程中的故障飞机数量，由此发生系统故障甚至危及飞行安全的灾难性事故的可能性，给出严重性等级fF,机队风险RF为

RF=εFμFψFfF

(3)

式中：εF为故障飞机预测数量；μF为未检出故障概率；ψF为发生灾难性后果的条件概率，因果链条件概率乘积之和，与故障类型和飞行循环相关；fF为严重性等级。

ε为机队中每架飞机从当前飞行循环到退役飞行循环发生故障的条件概率之和[18]，以累积分布函数表示：

(4)

式中：N为机队飞机数量；Ai为第i架飞机预测故障概率；F(t)为累积分布函数，t为飞行循环，tR为退役飞行循环，ti为当前飞行循环，tR≥ti。

机队中飞机设计型号存在差异，同一部件可能不完全相同，据极大似然估计函数，由形状参数获得寿命参数，即η=f(ti,β),如式(6)所示。

(5)

(6)

式中：m为机队故障飞机数。当β确定时，故障飞机数越少，机队特征寿命越长。由式(4)～式(6)可得Ai为

取β=2,4，tR/η=2/3,1,2，Ai随ti/tR变化趋势如图4所示。

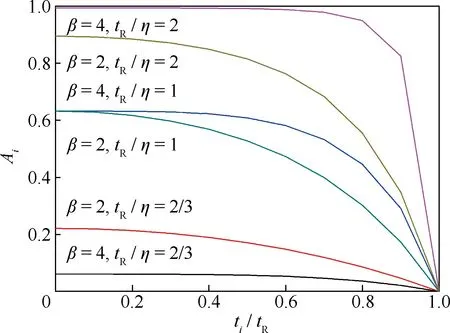
图4 β与tR/η对Ai的影响Fig.4 Effect of β and tR/η on contribution to Ai

当ti/tR=0时，Ai最大，新飞机有最高的损伤率。当ti/tR=1时，Ai为零，飞机退役不再运行，故障发生率为零。当η/tR≥1时，退役寿命低于特征寿命，机队初始运行时损伤率Ai较低，随飞机飞行循环增加不断降低，较少在退役之前发生故障。η/tR=1.5，β=4，对应的曲线，在飞机交付运行时，Ai-max仅为0.06，表明即使是刚交付的新飞机，在整个寿命期仅有6%的概率发生故障；当η/tR≤1时，退役寿命高于特征寿命，机队至少63.2%的飞机在退役前发生故障。η/tR相同时，Ai随β增大而升高。

2 发动机涡轮盘榫齿故障风险评估

2.1 单机风险评估

某型涡轮发动机维修间隔为1 000 h，在使用中由于Ⅱ级涡轮盘榫齿裂纹断裂导致叶片甩出，曾发生多次事故[19-20]，文献[21]指出涡轮盘榫齿在工作时承受叶片离心力引起的拉伸应力、弯曲应力、剪切应力、齿面上的挤压应力及温度分布不均匀引起的热应力，容易出现疲劳断裂。通过故障数据分析，涡轮盘榫齿裂纹故障概率服从威布尔分布。由文献[6]确定双参数β=2，η=1 418/h。由式(2)获得涡轮榫齿故障率曲线h(tI)，如图5所示， 发动机运行时间越长， 故障率上升速率越快，在到达维修间隔1 000 h时，涡轮盘榫齿故障率为7.0×10-4/h。

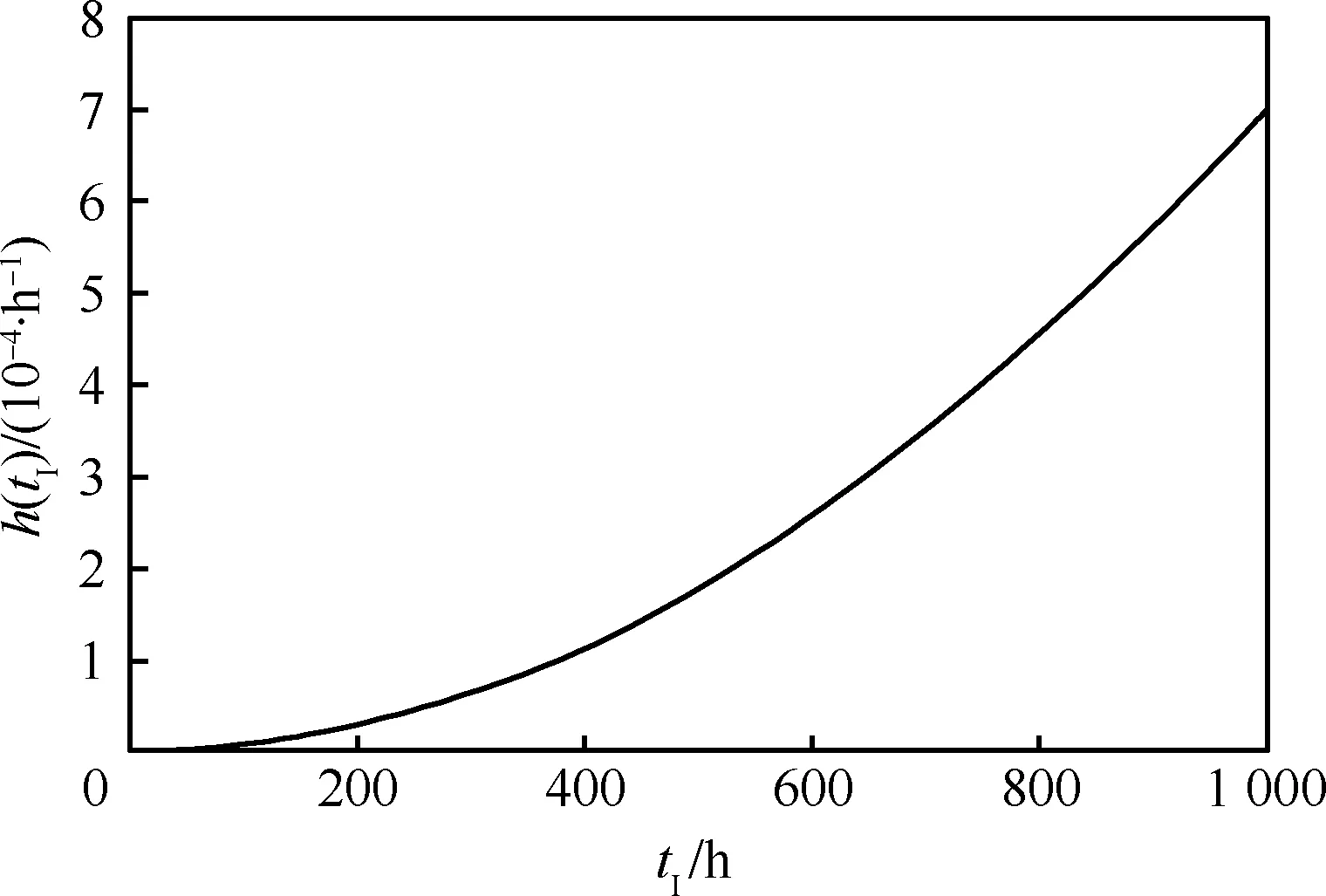
图5 涡轮盘榫齿故障率Fig.5 Failure rate of dovetail gear in turbine disk

由图2可知，通过现有的电位法探伤等检查方法检查涡轮盘榫齿裂纹故障时存在漏检的情况，不容易被检出，在造成灾难性后果前难以被检出，结构设计符合损伤容限理论，涡轮榫齿在相似应力水平上无相似结构运行，不受广泛的疲劳故障影响，具有多条加载路径设计，μ值取0.3。

榫齿裂纹因果链如图6所示，涡轮盘榫齿产生裂纹概率P1与当前运行循环有关。当ti/tR分别接近于20%、40%、60%、80%时，P1分别为0.8、0.5、0.1、0.01。通过蒙特卡罗方法，对涡轮盘榫齿开始出现裂纹故障时间，模拟100 000次，tR=1 000 h，β=2，η=1 418/h， 预测涡轮盘榫齿在运行661 h时生成可探测到的裂纹，ti/tR=661/1 000= 66%，则P1=0.1。由榫齿裂纹导致发生不安全后果的各状态条件概率由历史统计数据获得。涡轮盘榫齿故障导致4种不安全后果中的一种或多种：空中解体，坠毁，机身基本完整、存在人员伤亡，未正常起飞滑行、偏离跑道。4种不安全后果的严重性等级为死亡数与总人数之比，如图6所示。

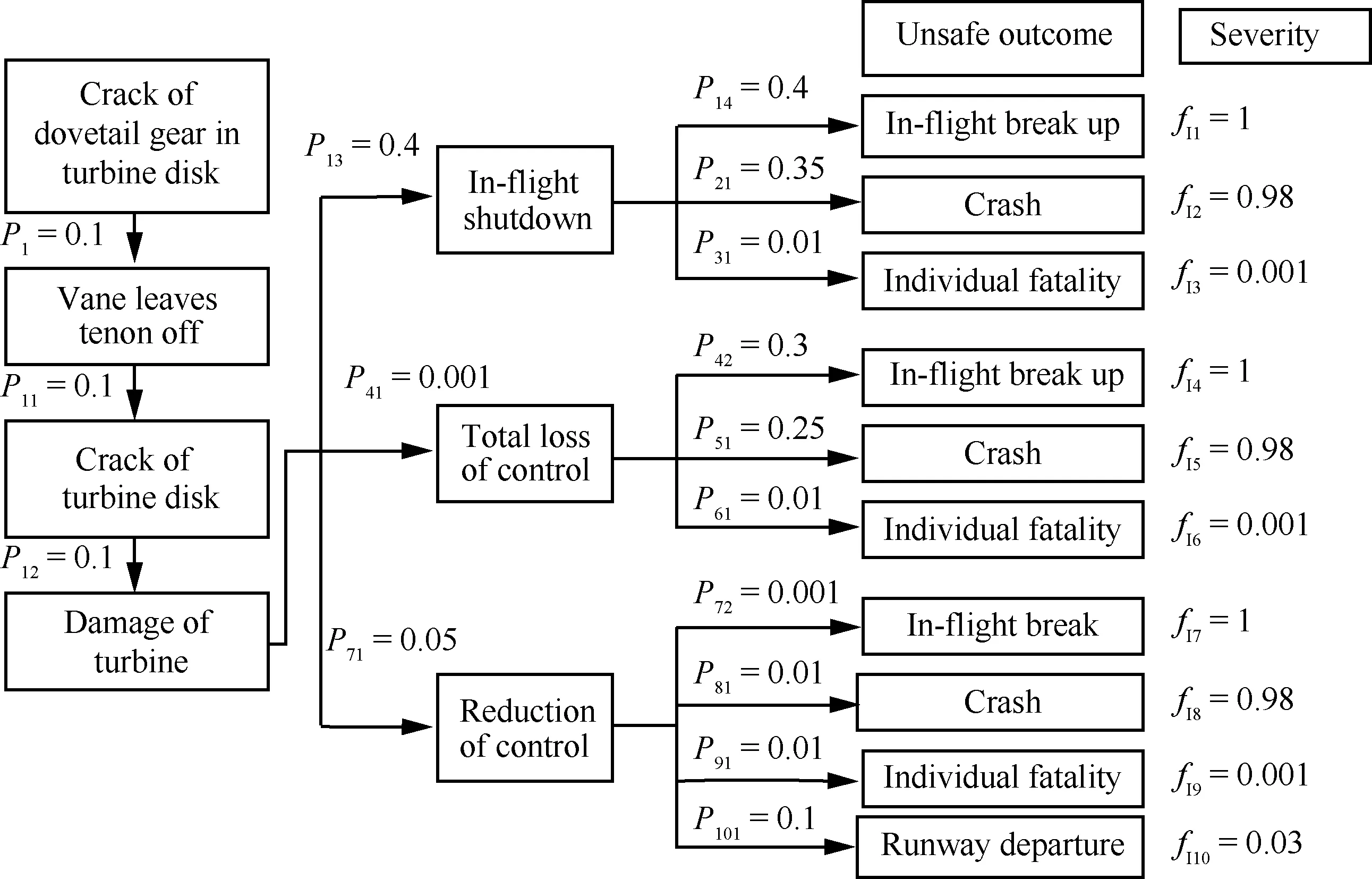
图6 涡轮盘榫齿裂纹因果链Fig.6 Causal chain of crack on dovetail gear in turbine disk

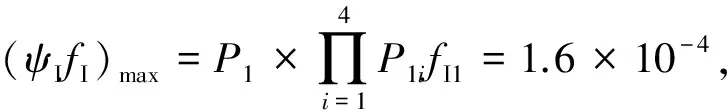
ψIfI=1.6×10-4,1.37×10-4,4×10-9,3×10-7,2.45×10-7,1×10-11,5×10-9,4.9×10-8,5×10-11,1.5×10-8。

∑(ψIfI)=2.98×10-4，为单架飞机当前由于榫齿裂纹故障产生的所有不安全后果概率。

单机风险RI=h(tI)μIψIfI=h(tI)×0.3×2.98×10-4=8.94×10-5h(tI),如图7所示。该发动机在下次维修之前，涡轮盘榫齿故障导致的后果风险小于部件故障可接受风险水平10-7/飞行小时[2]。

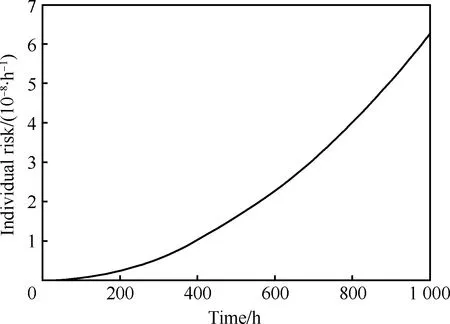
图7 单机故障风险水平Fig.7 Failure level of individual risk

2.2 机队风险评估

某机队在役飞机有507架，当前飞行循环如图8所示。检出故障飞机数m取1、3、5、7、9，tR=50 000飞行循环,70 000飞行循环，分析退役时间不同对机队运行安全的影响。

由式(6)，β=2，m=1，tR=50 000飞行循环时,有

由式(4)可得

通过蒙特卡罗方法，对涡轮盘榫齿产生裂纹时间，模拟100 000次。

当tR=50 000飞行循环，β=2，η=635 821时，模拟结果如图9所示。

预测涡轮盘榫齿在运行33 311飞行循环时生成可探测的裂纹，ti/tR=66.7%，P1=0.1。

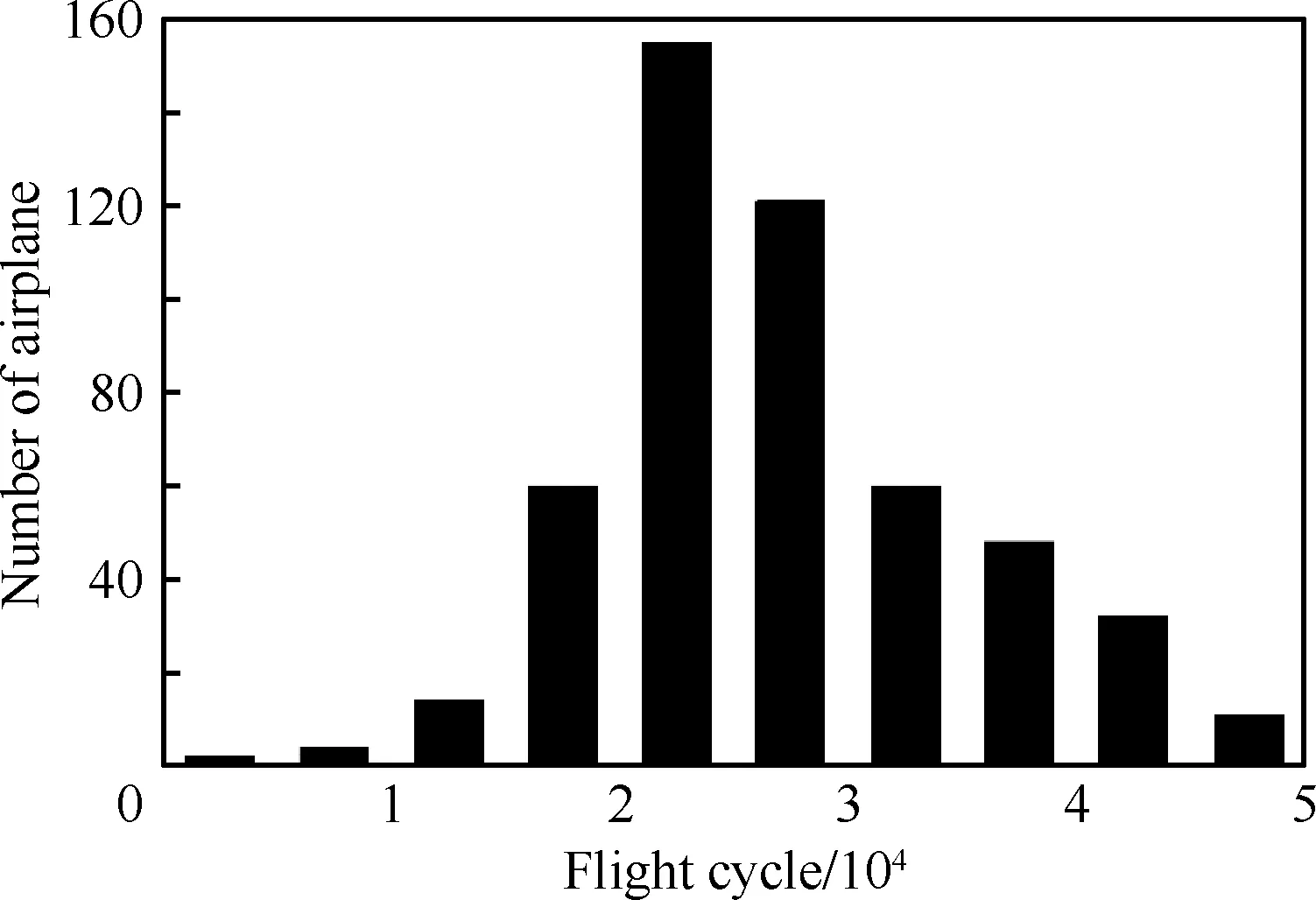
图8 机队飞行循环统计图Fig.8 Fleet data of flight cycle

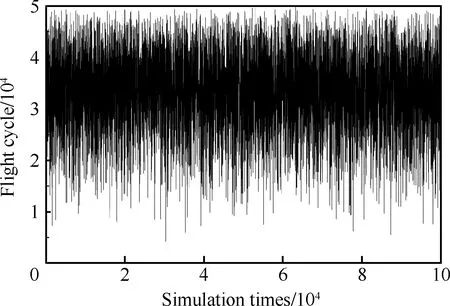
图9 预测涡轮盘榫齿故障的飞行循环Fig.9 Predicted flight cycle of cracking on dovetail gear in turbine disk

(ψFfF)max=0.000 16

∑(ψFfF)=0.000 298

RF=εμFψFfF=

2.1×0.3×0.000 298=0.000 188

当tR=70 000飞行循环时，ti=33 636飞行循环，ti/tR=48.05%，P1=0.5。

(ψFfF)max=0.000 6

∑(ψFfF)=0.001 488

RF=εμFψFfF=

5.1×0.3×0.001 488=0.002 28

相应η、ε和RF,如表1所示。

分别取tR=50 000,70 000，生成图10所示曲线RF=g(m),给出风险随故障飞机数变化趋势，民用飞机机队运行风险可接受水平为0.02[2]。风险水平与退役寿命密切相关，退役寿命越长，机队故障风险越高。

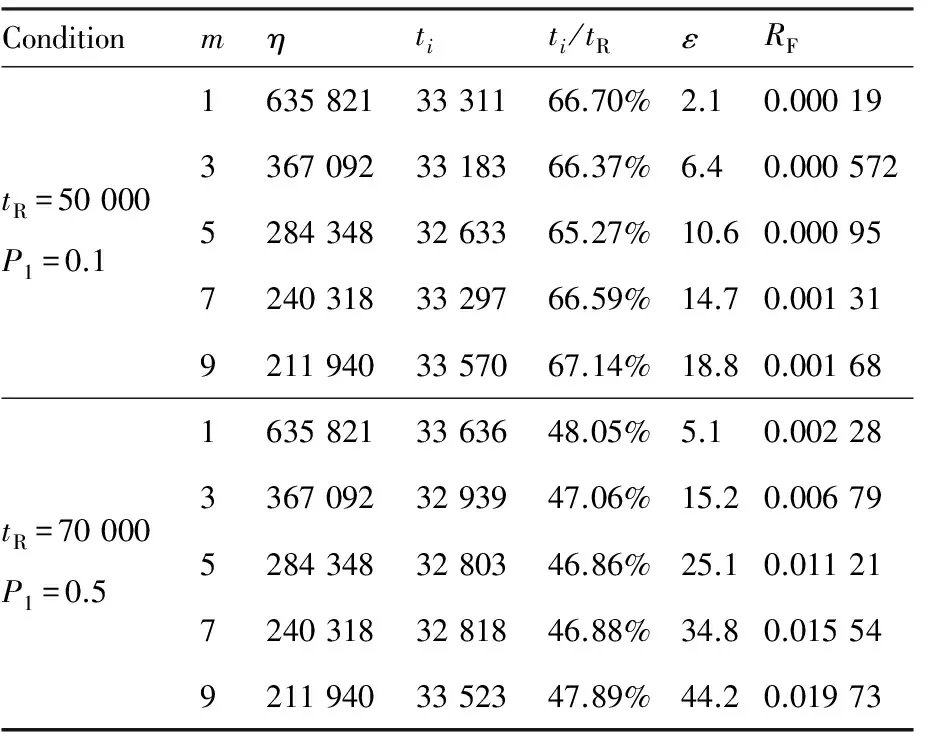
表1 机队故障风险参数(β=2)Table 1 Failure risk parameters of fleet(β=2)

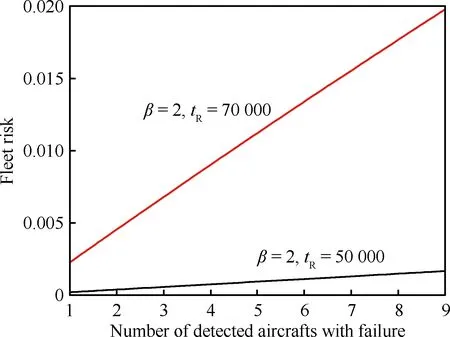
图10 机队故障风险水平Fig.10 Failure level of fleet risk

取(β,m)=(2,9),(2,1)。由表1或图11获得预测飞机出现涡轮盘榫齿故障数。表1中β=2，m=9，tR=50 000飞行循环时，预测故障飞机数量为18.8架，当ti=tR时，存在9+18.8≈28架飞机可能出现涡轮盘榫齿故障；由式(3)，F(t)随飞行循环变化趋势如图11所示，tR=50 000飞行循环，β=2，m=9，ti=tR时，机队累积故障率为5.41%，因此有507×5.41%≈28架飞机可能出现涡轮盘榫齿故障。

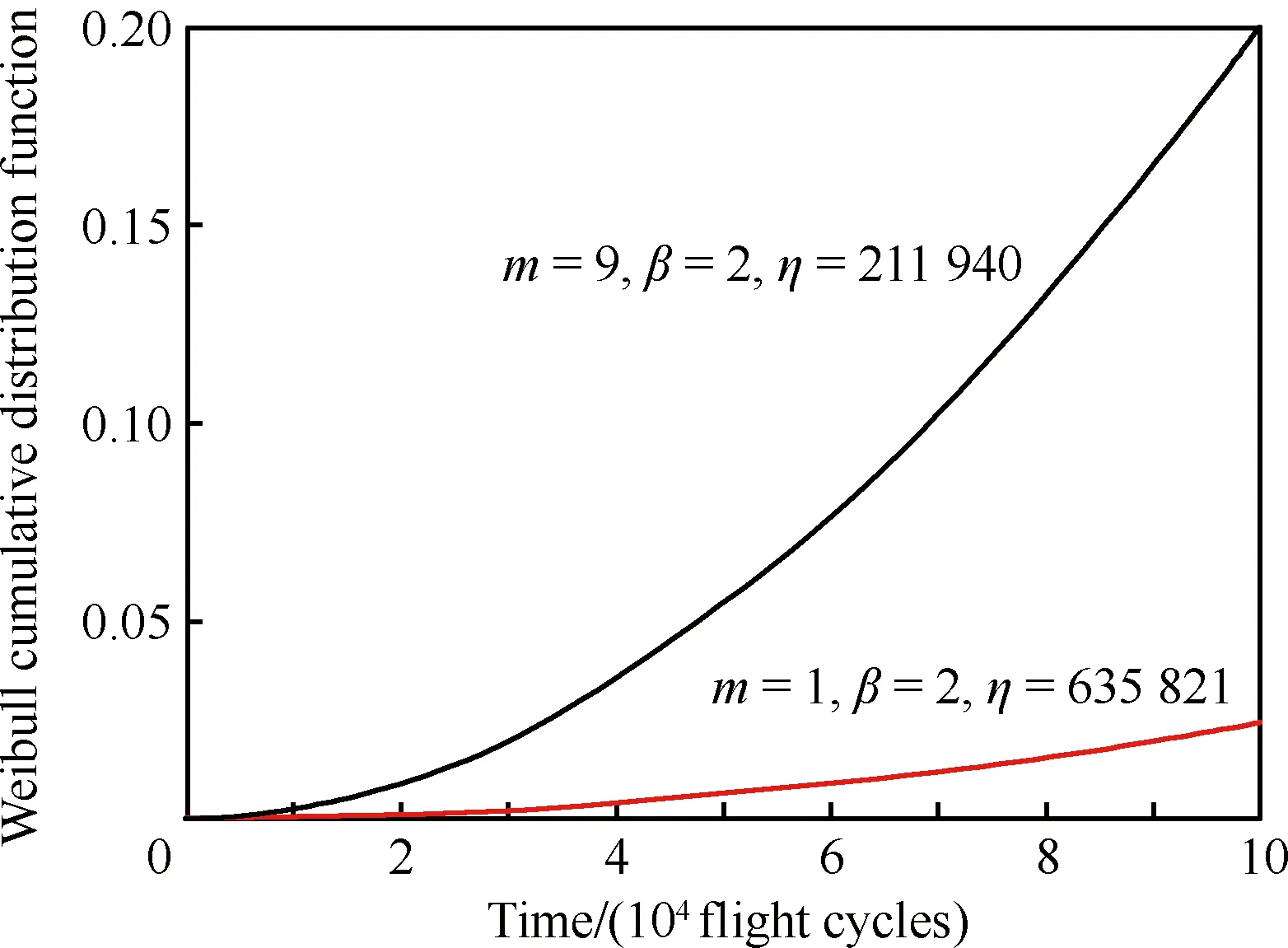
图11 威布尔累积分布函数Fig.11 Weibull cumulative distribution functions

3 结 论

威布尔分布很好地建立了单机运行故障率曲线和机队随飞行循环变化的风险水平。对发动机涡轮盘榫齿故障进行单机和机队风险计算，单机运行风险取决于部件的故障率和未检出概率；机队运行风险由机队当前运行规模及飞行循环确定。

1) 单机涡轮盘榫齿故障风险水平低于可接受水平10-7/飞行小时，但随着运行时间接近退役寿命，故障风险水平接近10-7/飞行小时。

2) 机队涡轮盘榫齿故障风险在故障飞机增至9架，服役寿命为70 000飞行循环时，风险水平超过机队风险可接受水平0.02。

3) 若当前退役寿命下对应风险值已超出上限值，则需根据风险计算结果采取相应纠正措施。

[1] CABLER J M.8110.107A Monitor safety/analyze data[S]. Washington, D.C.: Federal Aviation Administration, 2012.

[2] U.S. Department of Transportation. Advisory circular 39-8 Continued airworthiness assessments of powerplant and auxiliary power unit installations of transport category airplanes[S]. Washington, D.C.: Federal Aviation Administration, 2003.

[3] Transport Airplane Directorate. PS-ANM-25-05 Transport airplane risk assessment methodology handbook[S]. Washington, D.C.: Federal Aviation Administration, 2011.

[4] BRISTOL T. Safety management system manual[S]. Washington, D.C.: Federal Aviation Administration, 2014.

[5] GALILEO T, MICAELA D. Risk assessment techniques for civil aviation security[J]. Reliability Engineering and System Safety, 2011, 96(8): 892-899.

[6] 李龙彪, 毕苏艺, 孙有朝. 一种基于故障统计数据的发动机风险预测[J]. 南京航空航天大学学报, 2015, 47(4): 559-565.

LI L B, BI S Y, SUN Y C. Risk prediction of aero-engine based on failure statistics data[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2015, 47(4): 559-565 (in Chinese).

[7] HEDO J M, Val M R. Assessment of narrow-body transport airplane evacuation by numerical simulation[J]. Journal of Aircraft, 2011, 48(5): 1785-1794.

[8] 徐庆宏, 孙有朝, 李龙彪. 航空发动机部件故障风险评估方法研究[J]. 机械科学与技术, 2016, 35(8): 1291-1296.

XU Q H, SUN Y C, LI L B. Study on risk assessment method for aero-engine component failure[J]. Mechanical Science and Technology for Aerospace Engineering, 2016, 35(8): 1291-1296 (in Chinese).

[9] 郭媛媛, 李龙彪, 胡宇群, 等. 民用飞机运行风险评估方法[J]. 航空工程进展, 2016, 7(2): 253-258.

GUO Y Y, LI L B, HU Y Q, et al. Operation risk assessment method of civil aircraft[J]. Advances in Aeronautical Science and Engineering, 2016, 7(2): 253-258 (in Chinese).

[10] 王健名, 徐浩军, 薛源, 等. 基于极值理论的平尾结冰飞行风险评估[J]. 航空学报, 2016, 37(10): 3011-3022.

WANG J M, XU H J, XUE Y, et al. Flight risk evaluation of tailplane icing based on extreme value theory[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(10): 3011-3022 (in Chinese).

[11] 李岩, 张曙光, 宫綦. 一种改进的航空发动机结构概率风险评估方法[J]. 航空学报, 2016, 37(2): 597-608.

LI Y, ZHANG S G, GONG Q. An improved probabilistic risk assessment method of structural parts for aeroengine[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 597-608 (in Chinese).

[12] 薛源, 徐浩军, 胡孟权. 结冰条件下人-机-环系统的飞行风险概率[J]. 航空学报, 2016, 37(11): 3328-3339.

XUE Y, XU H J, HU M Q. Flight risk probability of pilot-aircraft-environment system under icing conditions[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3328-3339 (in Chinese).

[13] 孙杨慧, 杨坤, 侯乃先, 等. 涡轮盘概率风险的评估方法[J]. 航空动力学报, 2016, 31(9): 2195-2202.

SUN Y H, YANG K, HOU N X, et al. Probabilistic risk assessment method for turbine disk[J]. Journal of Aerospace Power, 2016, 31(9): 2195-2202 (in Chinese).

[14] 凌丹. 威布尔分布模型及其在机械可靠性中的应用研究[D]. 成都: 电子科技大学, 2010: 3-24.

LING D. Research on Weibull distribution and its applications in mechanical reliability engineering[D]. Chengdu: University of Electronic Science and Technology of China, 2010: 3-24 (in Chinese).

[15] 赵洪利, 刘宇文. 基于蒙特卡罗模拟的航空发动机故障风险预测[J]. 北京航空航天大学学报, 2015, 41(3): 545-550.

ZHAO H L, LIU Y W. Forecasting for aero-engine failure risk based on Monte Carlo simulation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(3): 545-550 (in Chinese).

[16] Society of Automotive Engineers. ARP5150 safety assessment of transport airplanes in commercial service[S]. SAE, 2003.

[17] ABERNETHY R B. The new weibull handbook[M]. 5th ed. Florida: Society of Automotive Engineers International, 2010: 2-11.

[18] VIOLETTE M G, SAFARIAN P, HAN N, et al. Transport airplane risk analysis[J]. Journal of Aircraft, 2015, 52(2): 395-402.

[19] 何卫锋, 李应红, 聂祥樊, 等. 激光冲击叶片榫头变形控制与疲劳试验[J]. 航空学报, 2014, 35(7): 2041-2048.

HE W F, LI Y H, NIE X F, et al. Deformation control and fatigue test of blade tenon by laser shock peening[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(7): 2041-2048 (in Chinese).

[20] 孙瑞杰, 闫晓军. 涡轮叶片榫齿部位疲劳/蠕变试验的新特点[J]. 航空动力学报, 2007, 22(3): 419-424.

SUN R J, YAN X J. New characteristics of fatigue-creep tests on serration of turbine blades[J]. Journal of Aerospace Power, 2007, 22(3): 419-424 (in Chinese).

[21] 刘滨春, 王慧. 某型发动机涡轮盘榫齿裂纹分析[J]. 工程与试验, 2012, 52(2): 26-27.

LIU B C, WANG H. Analysis of serration crack in turbine disc for engineer[J]. Engineering and Test, 2012, 52(2): 26-27 (in Chinese).

FailureriskassessmentmethodofcivilaircraftbasedonMonteCarlomethod

GUOYuanyuan,SUNYouchao*,LILongbiao

CollegeofCivilAviation,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China

Inordertoimproveaviationsafetyandreducetherisklevelofpartsfailureintheprocessofcivilaircraftoperation,theindividualandfleetriskshavebeencalculated.Thekeypointsofindividualriskarehowtoconfirmthefailuredistributionandrate,whichturnsoutthatWei-bulldistributionisapplicable.Accordingtothefailuremechanismofpart,thenon-detectionprobabilityandtheconditionalprobabilitythedetectwillleadstoanunsafeoutcomeaswellasrelatedinjuryratehavebeenlisted,inordertodeterminetherisklevel.Basedontheindividualrisk,thekeypointsoffleetriskarefleetscaleandcurrentflightcircles.Thenumberoffailureflightshasbeenpredictedbasedonoperationaldata.Theriskvaluehasbeenacquiredunderdifferentoperatedsituationsuchasparameterdistribution,numberoffailureflightsaswellasretirementcycles.ThefailuretimeofindividualandfleethasbeensimulatedbyMonteCarlomethodinthecaseofserrationcrackinturbinediscofaero-engine.Therisklevelsofindividualandfleetaboutthisparthavebeenanalyzed,andthetwokindsrisklevelshavebeengivenatcontinuedairworthinessstagebasedonoperationaldata.

civilaircraft;fleetrisk;individualrisk;MonteCarlomethod;cumulativedistributionfunction;failurerate

2017-01-12；Revised2017-03-02；Accepted2017-04-18;Publishedonline2017-05-031644

URL：http://hkxb.buaa.edu.cn/CN/html/20171015.html

s：JointlyfundofNationalNaturalScienceFoundationofChinaandCivilAviationAdministrationofChina(U1333119);DefenseIndustrialTechnologyDevelopmentProgram(JCKY2013605B002);CivilAircraftSpecialFoundationofMinistryofIndustryandInformationTechnology(MJ-F-2011-33);FundofShanghaiEngineeringResearchforCivilAircraftHealthMonitoring(GCZX-2015-05);TechnicalProjectFoundationofStateAdministrationofScience,TechnologyandIndustryforNationalDefense(Z052013B003)

.E-mailsunyc@nuaa.edu.cn

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.221126

V239

A

1000-6893(2017)10-221126-09

2017-01-12；退修日期2017-03-02；录用日期2017-04-18；< class="emphasis_bold">网络出版时间

时间：2017-05-031644

http://hkxb.buaa.edu.cn/CN/html/20171015.html

国家自然科学基金与中国民用航空局联合资助(U1333119)； 国防基础科研计划(JCKY2013605B002)； 工信部民机专项(MJ-F-2011-33)； 上海民用飞机健康监控工程技术研究中心基金(GCZX-2015-05)； 国防科工局技术基础科研项目(Z052013B003)

.E-mailsunyc@nuaa.edu.cn

郭媛媛，孙有朝，李龙彪．基于蒙特卡罗方法的民用飞机故障风险评估方法J．航空学报,2017,38(10):221126.GUOYY,SUNYC,LILB.FailureriskassessmentmethodofcivilaircraftbasedonMonteCarlomethodJ.ActaAeronauticaetAstronauticaSinica,2017,38(10):221126.

(责任编辑：张晗)