基于多相材料的连续体结构动态轻量化设计方法

龙凯，谷先广，王选

1.华北电力大学 能源的安全与清洁利用北京市重点实验室，北京 102206 2.华北电力大学 新能源电力系统国家重点实验室，北京 102206 3.合肥工业大学 汽车与交通工程学院，合肥 230009 4.大连理工大学 工业装备结构分析国家重点实验室，大连 116024

基于多相材料的连续体结构动态轻量化设计方法

龙凯1,2,*，谷先广3，王选4

1.华北电力大学 能源的安全与清洁利用北京市重点实验室，北京 102206 2.华北电力大学 新能源电力系统国家重点实验室，北京 102206 3.合肥工业大学 汽车与交通工程学院，合肥 230009 4.大连理工大学 工业装备结构分析国家重点实验室，大连 116024

为了实现基于多相材料的结构轻量化设计，遵循独立连续映射法，提出了以结构总重最小化为目标和给定特征值为约束的拓扑优化模型。方法采用2类独立拓扑变量实现了单元刚度矩阵、质量矩阵和重量插值。推导了固有特征值和总重量的敏度表达式，通过1阶和2阶泰勒展开得到其近似表达式。对约束函数一次项过滤转换为偏微分方程的求解，消除了棋盘格现象和网格依赖性等数值不稳定性。通过二维数值算例验证了提出方法的可行性和优越性。结果表明，与单相组分材料拓扑优化结构相比，多相材料拓扑优化结构具有更轻的重量。通过附加相邻频率间隔约束或增加高阶频率约束，避免了模态交换现象。

拓扑优化；独立连续映射法；连续体结构；固有频率；模态分析

自Bendsoe和Kikuchi[1]提出连续体结构拓扑优化概念以来，迄今为止涌现出各类拓扑优化方法，包括均匀化法、实体各向同性惩罚微结构(Solid Isotropic Microstructures with Penalization,SIMP) 的变密度法、双向结构进化式(Bi-directional Evolutionary Structural Optimization,BESO)法和水平集法等。文献[2-6]给出了在不同发展阶段各类方法的理论和应用综述。早期的动态优化研究大多以结构固有频率为目标或约束，体现在各类拓扑优化方法中[7-11]。在动态响应方面，以降低结构振动幅度、减小噪声的拓扑优化方法也被相继提出[12-19]。文献[20]综述了现有的动态拓扑优化研究。

多相材料的布局优化是拓扑优化研究中另一类值得关注的问题。Thomsen[21]较早开展了多相材料的拓扑优化研究。Sigmund和Torquato[22]采用常规材料，实现了负热膨胀系数的材料微结构优化设计。Gibiansky和Sigmund[23]提出了达到体积模量上限的多相材料组成的微结构。除了SIMP法外，多相材料布局优化在水平集法[24]、相场法[25]和BESO法[26]中也有所体现。Yin和Ananthasuresh[27]提出的峰值函数法用单变量描述多相材料以减少密度变量数目。Gao等[28-29]提出了线性对等混合材料插值和质量约束拓扑优化模型，指出质量约束在寻找全局最优解等方面的优越性。Takakoli和Mohseni[30]将多相布局优化问题转化为序列两相材料优化问题，采用优化准则法求解，实现了各相材料体积比约束下的布局优化。Zuo和Saitou[31]归一化处理密度变量，减少了密度变量数目，提出了序列SIMP方法。

不同于常见拓扑优化方法，独立连续映射(Independent Continuous Mapping,ICM)方法以独立于单元具体物理参数的变量表征单元的有无[32]。其独立性体现在拓扑变量摆脱了物理量的约束，提出了磨光、过滤函数等新概念。自1996年被提出以来，ICM方法实现了重量最小化目标下的应力、位移、频率和屈曲因子等约束条件的拓扑优化结构设计[33]，研究成果集中体现在文献[34]中。

目前多相材料布局优化较多地以各相材料体积比或总质量为约束条件建立优化模型。与此不同，本文将针对结构动态拓扑优化问题，基于ICM方法建立多相材料布局的拓扑优化模型。优化目标为总重最小化，这种以轻量化设计为目的的优化模型具有更为直观的工程意义。方法定义了2类独立拓扑变量以表征单元的有无和不同材料相。采用1阶、2阶泰勒近似表达固有特征值和重量函数，建立的二次优化近似模型采用序列二次规划方法求解。最后通过数值算例来证明本文提出的方法在多相材料布局优化的可行性。

1 材料插值模型

ICM方法定义2类独立拓扑变量si(0≤si≤1)和ti(0≤ti≤1)用于表征单元的有无和不同相材料，其与单元刚度矩阵ki、质量矩阵mi和重量wi的关系为

(1)

式中:N为设计区域单元总数；上标Ⅰ和Ⅱ表示可选用材料Ⅰ和Ⅱ;si=1或0表示单元i由材料填充或空洞；ti=1或0表示单元i选用材料Ⅰ或材料Ⅱ;α和β分别为单元刚度矩阵和质量矩阵惩罚因子。

以重量最小化为目标，给定特征值约束限值的拓扑优化模型为

(2)

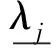
在动力学优化问题中，普遍存在着局部模态的现象，这种现象是由低密度区的刚度惩罚不当引起的[35]。在SIMP法和BESO法中，通常修正低密度区的弹性模量来避免局部模态现象[35-36]。这里通过对质量矩阵予以刚度矩阵相同的惩罚来消除局部模态现象，即α=β=4。数值实验结果表明，这种参数设置能有效地避免局部模态现象，并得到清晰的拓扑优化构型。

2 结构响应量的显式表达与优化建模

模态分析有限元方程为

Kuj=λjMuj

(3)

式中：K和M分别为总体刚度矩阵和质量矩阵；uj为第j阶特征向量。由伴随法易推导得

(4)

式中：K和M对si和ti的偏导数计算可归结为单元刚度矩阵和质量矩阵的偏导数计算上，由式(1)可得

(5)

与SIMP方法不同，ICM方法引入si和ti的倒数函数作为设计变量，定义设计变量xi和yi为

(6)

由此可得

(7)

固有特征值采用2类设计变量的1阶泰勒展开得到其近似表达式为

(8)

(9)

将式(4)、式(5)和式(7)代入式(9)，可求得敏度值。

基于设计变量表达的重量函数为

(10)

易推导重量函数的1阶偏导数为

(11)

同理可得重量函数的2阶偏导数为

(12)

根据式(11)和式(12)，在当前设计变量下，采用2阶泰勒展开得到重量函数的近似表达式为

(13)

经过上述推导，优化模型式(2)可转换为

(14)

式(14)中的约束函数和目标函数分别采用式(8)和式(13)的近似表达式。

动态拓扑优化中存在着模态交换问题，除了关心特征值大于等于指定值外，ICM方法采用增加约束的处理方式来避免模态交换。例如，2阶特征值始终不小于1阶特征值[37-38]；或2阶特征值大于指定值。上述2种方法的目的在于相邻特征值间保持间隔，约束方程分别表达为

λ2≥bλ1

(15a)

(15b)

注意到模型式(14)是标准的二次规划形式，这里采用序列二次规划法求解，具体过程可参考文献[39-40]。在优化求解后，更新结构直至满足

|W(a+1)-W(a)|/W(a+1)≤ε

(16)

式中：ε为收敛率。

3 消除棋盘格现象和网格依赖性问题

连续体拓扑优化问题中普遍存在着棋盘格现象和网格依赖性问题[41-42]。基于数字图像原理的过滤方法被广泛应用解决上述问题。定义固有特征值对设计变量的偏导数与设计变量乘积为

(17)

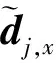
(18a)

(18b)

容易证明，过滤场函数满足

(19)

即过滤前后，式(8)中的一次项总和不变，这对稳定优化求解非常有利。

过滤措施带来的平均效果不可避免地导致优化构型边界不清晰。为了获得清晰的拓扑优化构型，采用2阶段优化策略[39-40]，即在第1阶段采用过滤措施消除棋盘格现象和网格依赖性问题。第2阶段不采用过滤措施直至优化收敛。这2个阶段采用的收敛率ε不同，分别取值为0.5‰和0.1‰。

4 数值算例

采用数值算例来说明提出方法的可行性和优越性。可选用的材料及属性如表1所示。每个算例均为平面结构，厚度为1 mm。结构采用四节点方形单元离散，单元尺寸为1 mm×1 mm。当结构全部由碳钢材料组成，其质量和重量分别为m0和W0，结构拓扑优化后的重量为W，以重量比W/W0来说明减重效果。在拓扑优化构型中，碳钢、铝和镁分别采用红色、蓝色和绿色表示，空洞部分不显示。

表1 可选用材料的属性Table 1 Properties of candidate material

算例1图1所示的长梁结构，结构尺寸为280 mm×40 mm。梁两端全固定，平板中心附加一个质量为m0的质量点。可选材料为碳钢和铝，当结构分别采用碳钢和铝时，对应的1阶频率分别为1 237和813 Hz。对于多相材料布局优化问题，设结构1阶频率下限值为750 Hz。本算例首先考察惩罚参数对优化结果的影响。选取参数α=4、β=1，拓扑优化过程迭代振荡无法收敛。结构固有频率值在优化迭代过程中会突然变小，该现象由低密度区的虚假模态引起。当参数α=β=4时，优化迭代78步收敛，优化结果重量比为0.271，拓扑优化结果如图2(a)所示。为了验证提出方法的可行性和有效性，优化模型采用式(2)形式，采用移动渐近线(MMA)算法更新变量，在指定的最大优化迭代步(≥300)收敛，优化重量比为0.278，拓扑优化构型如图2(b)所示。

由图2可知，2种不同方法得到的拓扑优化构型类似，说明本文提出方法具有可行性。长梁结构1阶振型为弯曲振型，图2(a)中更多的强相材料布置在上下表面以提高结构抗弯性，优化后的结构重量更轻。由此可知，ICM方法得到的优化结构合理，且优化迭代效率高。

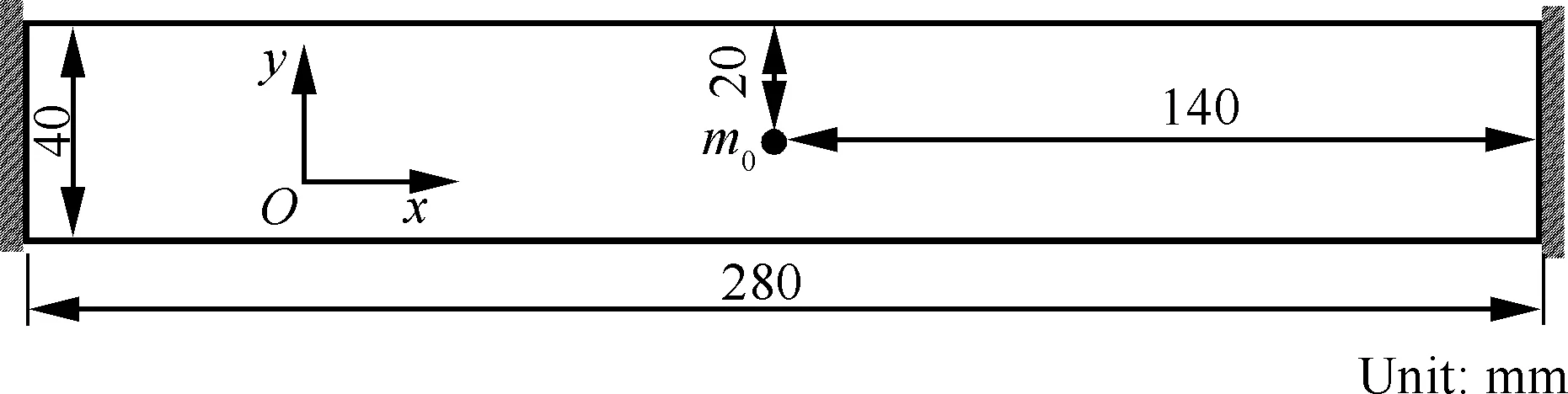
图1 长梁结构Fig.1 A long beam

图2 不同方法下的优化构型Fig.2 Optimal configurations with different methods

算例2本算例是算例1的扩展，用于考察不同频率约束下多相材料拓扑优化结果与单相拓扑优化结果的对比。设结构1阶频率下限在500～900 Hz之间变化，不同频率约束下的多相材料拓扑优化结果如表2所示。为了便于比较，在相同的频率约束条件下，单相组分材料下的拓扑优化结果如表3和表4所示。

由表2可知，在不同的频率约束条件下，多相材料拓扑优化结构包含碳钢、铝和空洞，强相材料碳钢始终布置在约束位置、质量点位置等区域。对比表2～表4的结果可知，在相同的1阶频率约束条件下，多相材料拓扑优化结构比2种组分材料下的优化结构更轻。当1阶频率要求不低于900 Hz时，整个结构全部采用铝材料无法满足设计要求。综合上述2点，多相材料不仅能更好地满足设计要求，同时达到了结构轻量化设计的目的。优化结果说明所提方法具有协调多相材料布局优化的能力。

表2 不同频率约束下的多相材料优化结果Table 2 Optimal results for multiple phases materials under different frequency constraints

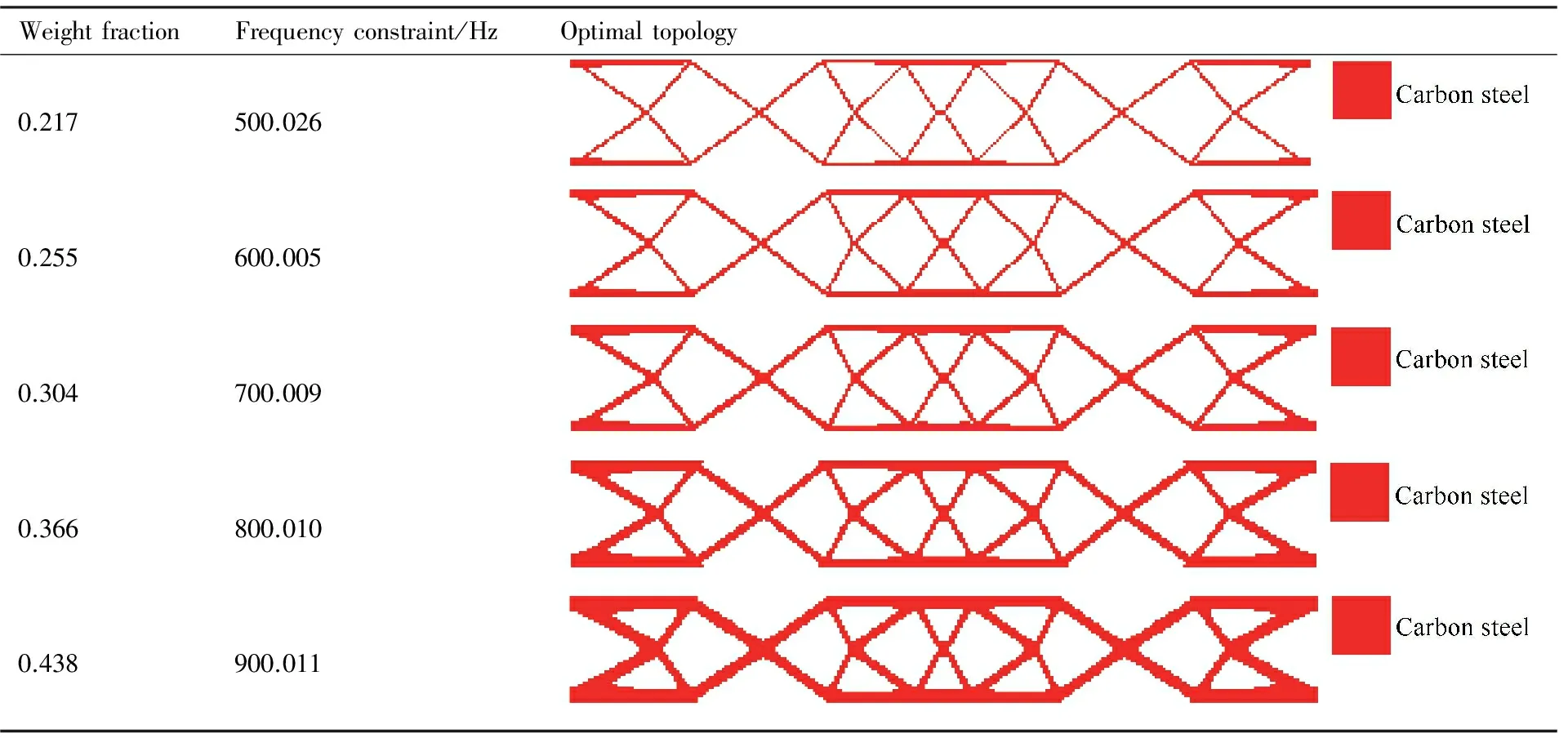
表3 相材料1下的优化结果Table 3 Optimal results for Phase 1

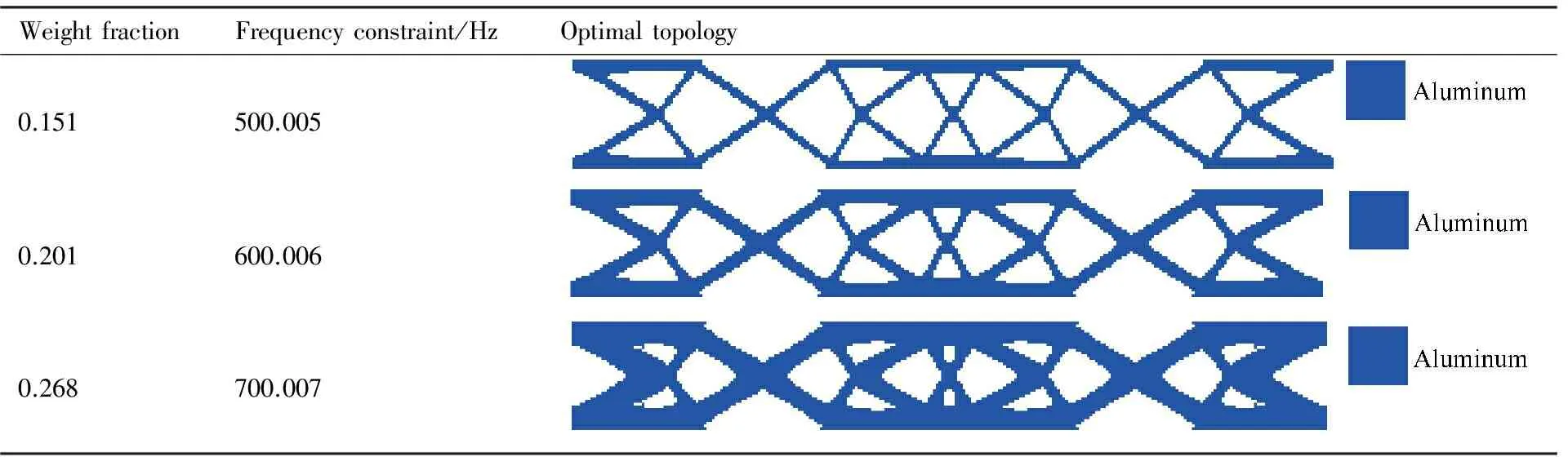
表4 相材料2下的优化结果Table 4 Optimal results for Phase 2

算例3如图3所示的短悬臂梁，结构尺寸为160 mm×100 mm。梁左端全约束，右端中心附加一个质量为0.8m0的质量点。分别选用碳钢、铝和镁来填充结构，1阶频率分别为1 284.9、834和669 Hz。设结构1阶频率不低于700 Hz。显然，整个结构全部采用镁材料无法满足设计要求。对于多相材料布局优化问题，考虑不同的多相材料组合：碳钢和铝、碳钢和镁，拓扑优化结果如表5所示。为便于比较，碳钢和铝单相材料拓扑优化结果也列于表5中。

由表5可知，2类多相材料组合和2类单相材料拓扑优化结果均能满足动态设计要求，多相材料拓扑优化结构均比组分单相材料拓扑优化结构轻。铝和镁材料比刚度较为接近，在多相材料拓扑优化结果中，这2种弱相材料所占的体积不同，最优结构重量接近。这说明多相材料的最优拓扑结构随着组分材料的不同而不同。

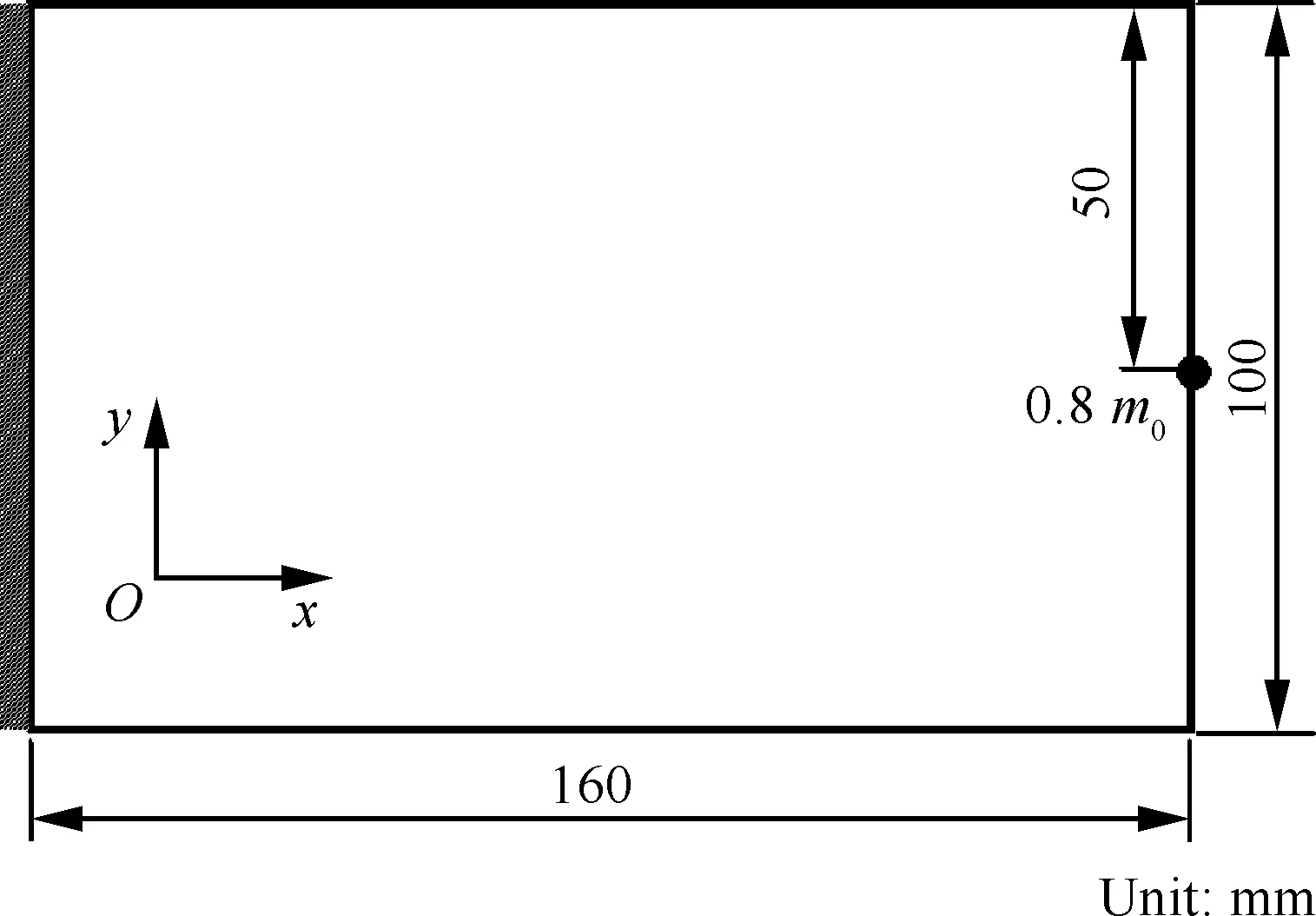
图3 短悬臂梁Fig.3 A short cantilever beam

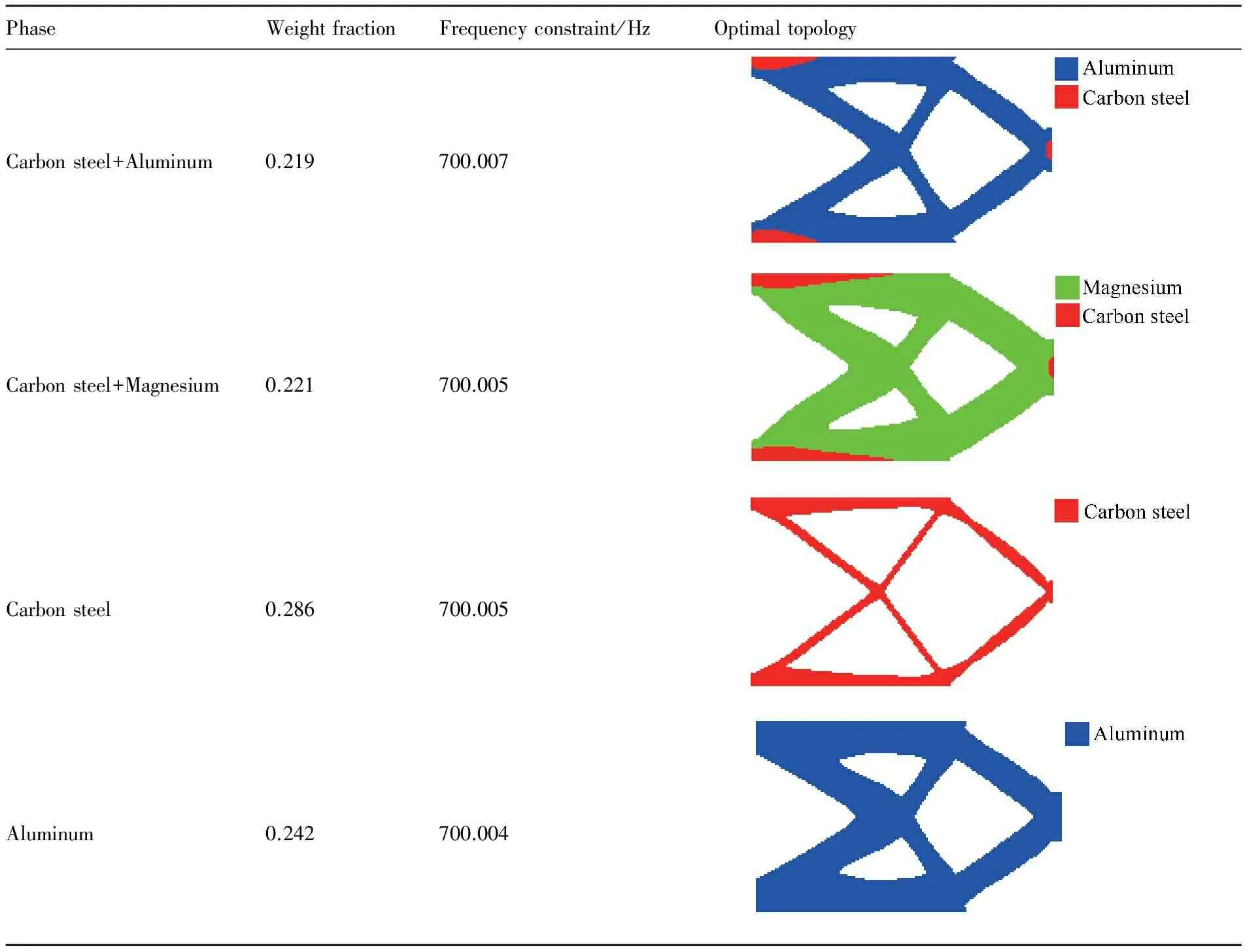
表5 不同相材料组合下的优化结果Table 5 Optimal results for different combinations of phases materials

算例4如图4所示的平面结构，结构尺寸为120 mm×40 mm，在下端面1/4、1/2和3/4位置处分别附加质量为0.8m0、0.6m0和0.8m0的质量点。可选材料为碳钢和铝。设结构1阶频率不低于2 000 Hz。本算例用来考察附加约束对拓扑优化结果的影响。计算3种情况：① 2阶频率无任何约束(Case 1)；② 根据式(15a)，设置λ2≥bλ1，强迫2阶频率始终大于1阶频率(Case 2)；③ 根据式(15b)增加2阶频率约束λ2≥2 500 Hz(Case 3)。3种情况下，优化迭代过程中的前2阶频率变化如图5所示。

由图5(a)可知，当没有2阶频率约束时，结构1、2阶频率在优化迭代过程中较为接近，容易产生模态交换现象，无法得到理想的拓扑优化结果。由图5(b)可知，λ2≥bλ1导致2阶频率与1阶频率保持一定的距离。由图5(c)可知，前2阶频率均满足设计要求，说明所提方法的有效性。

Case 2和Case 3下的拓扑优化结果如表6所示。由表6可知，拓扑优化结果均满足设定的约束条件，拓扑优化构型略有区别。Case 3的约束条件比Case 2的约束条件更为苛刻，故而优化结构稍重。

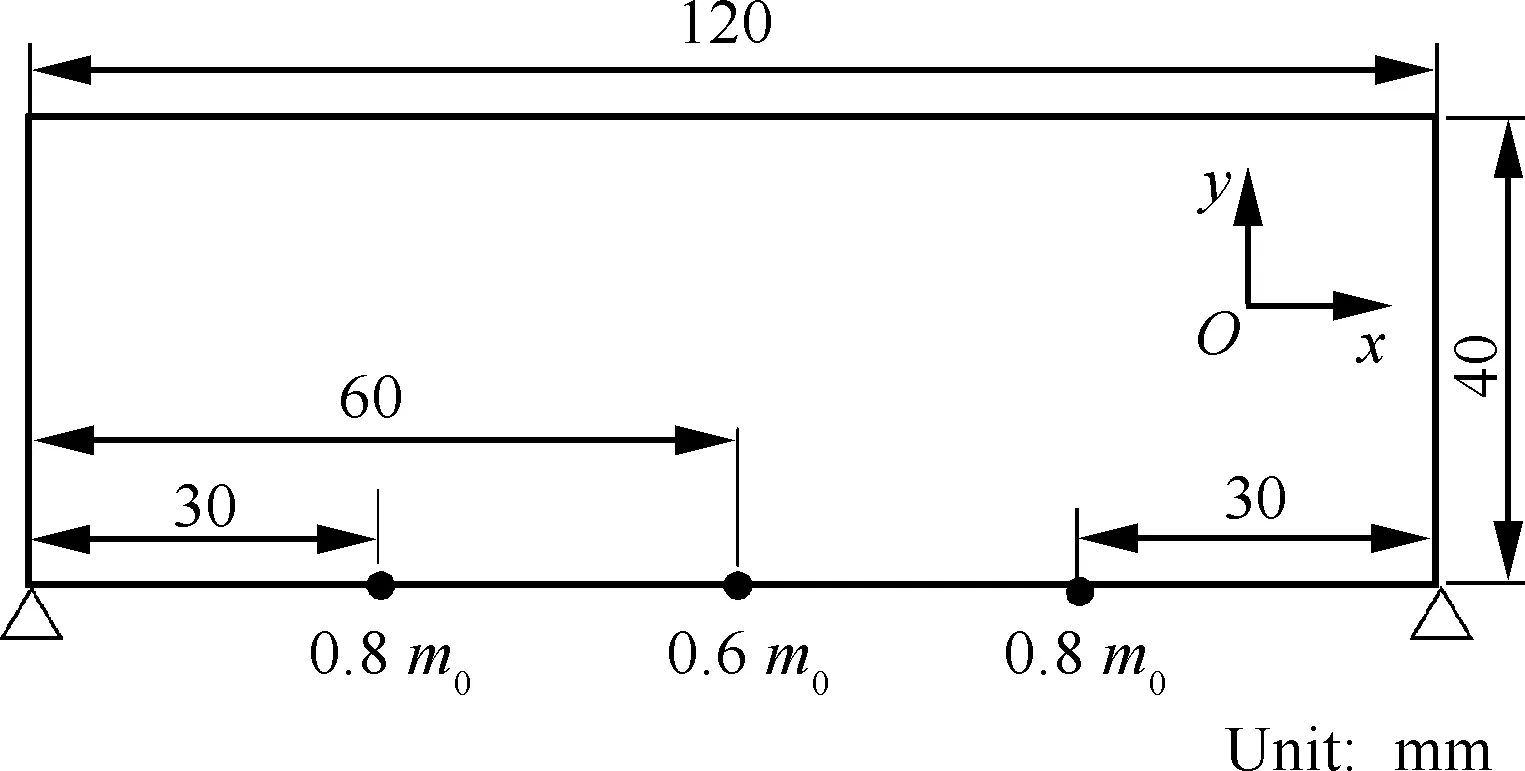
图4 平面结构Fig.4 A plane structure

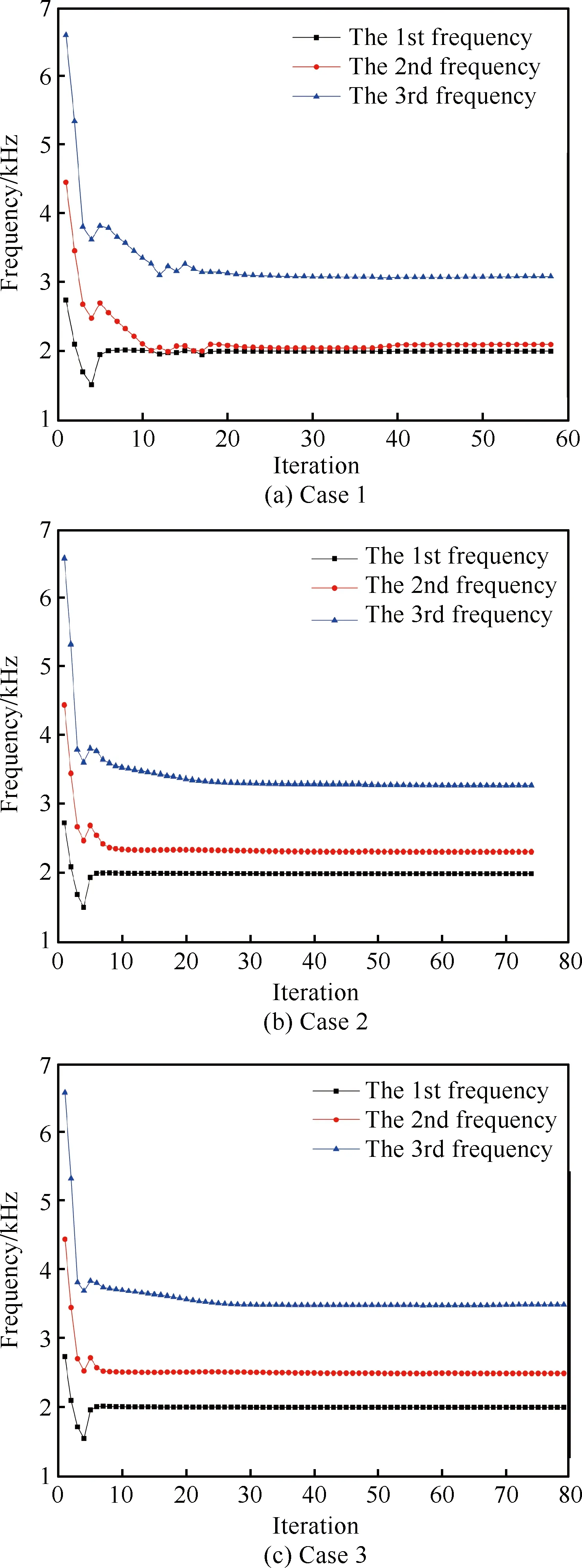
图5 固有频率迭代历程Fig.5 Iteration history of natural frequency

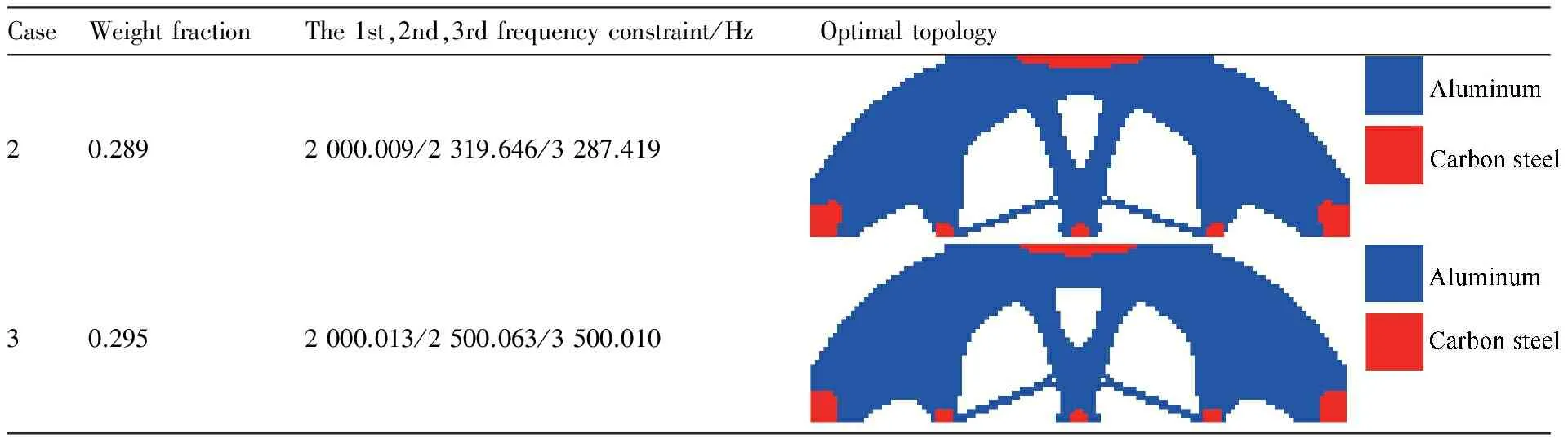
表6 不同约束条件下的优化结果Table 6 Optimal results for different constraints

5 结 论

1) 在结构轻量化设计要求下，提出基于多相材料的动态拓扑优化的ICM方法。与目前的多相材料拓扑优化方法不同，建立了指定固有特征值约束下的重量最小化优化模型。遵循ICM建模方式，将结构固有特征值和重量函数分别采用1阶、2阶泰勒展开得到其近似表达式，从而将优化模型转换为标准二次规划形式，采用序列二次规划法求解，方法稳健高效。

2) 在相同的固有特征值约束条件下，多相材料拓扑优化结构更轻。在动态设计要求下，提出方法实现了各相材料的合理分配和结构轻量化设计。

3) 根据优化设计要求，优化模型可拓展为多约束拓扑优化模型并实现优化求解，通过强迫相邻频率间距或增加高阶频率约束，能避免模态交换现象，并得到理想的拓扑优化结果。

[1] BENDSOE M P, KIKUCHI N. Generating optimal topologies in structural design using a homogenization method[J]. Computer Methods in Applied Mechanics and Engineering, 1988, 71(2): 197-224.

[2] ESCHENAUER H A, OLHOFF N. Topology optimization of continuum structures: A review[J]. Applied Mechanics Reviews, 2001, 54(4): 331-390.

[3] ROZVANY G I N. A critical review of established methods of structural topology optimization[J]. Structural and Multidisciplinary Optimization, 2009, 37(3): 217-237.

[4] SIGMUND O, MAUTE K. Topology optimization approaches[J]. Structural and Multidisciplinary Optimization, 2013, 48(6): 1031-1055.

[5] DEATON J D, GRANDHI R V. A survey of structural and multidisciplinary continuum topology optimization: Post 2000[J]. Structural and Multidisciplinary Optimization, 2014, 49(1): 1-38.

[6] XIA L, XIA Q, HUANG X, et al. Bi-directional evolutionary structural optimization on advanced structures and materials: A comprehensive review[J]. Archives of Computational Methods in Engineering, DOI 10.1007/s11831-016-9203-2.

[7] DIAZ A R, KIKUCHI N. Solutions to shape and topology eigenvalue optimization problems using a homogenization method[J]. International Journal for Numerical Methods in Engineering, 1992, 35(7): 1487-1502.

[8] MA Z D, KIKUCHI N, CHENG H C. Topological design for vibrating structures[J]. Computer Methods in Applied Mechanics and Engineering, 1995, 121(1-4): 259-280.

[9] XIE Y M, STEVEN G P. Evolutionary structural optimization for dynamic problems[J]. Computers & Structures, 1996, 58(6): 1067-1073.

[10] DU J, OLHOFF N. Minimization of sound radiation from vibrating bi-material structures using topology optimization[J]. Structural and Multidisciplinary Optimization, 2007, 33(4-5): 305-321.

[11] DU J, OLHOFF N. Topological design of freely vibrating continuum structures for maximum values of simple and multiple eigenfrequencies and frequency gaps[J]. Structural and Multidisciplinary Optimization, 2007, 34(2):91-110.

[12] DU J, OLHOFF N. Topological design of vibrating structures with respect to optimum sound pressure characteristics in a surrounding acoustic medium[J]. Structural and Multidisciplinary Optimization, 2010, 42(1): 43-54.

[13] JOG C S. Topology design of structures subjected to periodic loading[J]. Journal of Sound and Vibration, 2002, 253(3): 687-709.

[14] KANG B S, PARK G J, ARORA J S. A review of optimization of structures subjected to transient loads[J]. Structural and Multidisciplinary Optimization, 2006, 31(2): 81-95.

[15] KANG Z, ZHANG X, JIANG S, et al. On topology optimization of damping layer in shell structures under harmonic excitations[J]. Structural and Multidisciplinary Optimization, 2012, 46(1): 51-67.

[16] LIU H, ZHANG W H, GAO T. A comparative study of dynamic analysis methods for structural topology optimization under harmonic force excitations[J]. Structural and Multidisciplinary Optimization, 2015, 51(6): 1321-1333.

[17] NIU B, OLHOFF N, LUND E, et al. Discrete material optimization of vibrating laminated composite plates for minimum sound radiation[J]. International Journal of Solids and Structures, 2010, 47(16): 2097-2114.

[18] NIELS O, DU J. Generalized incremental frequency method for topological design of continuum structures for minimum dynamic compliance subject to forced vibration at a prescribed low or high value of the excitation frequency[J]. Structural and Multidisciplinary Optimization, 2016, 54(5): 1113-1141.

[19] ZHAO J, WANG C. Dynamic response topology optimization in the time domain using model reduction method[J]. Structural and Multidisciplinary Optimization, 2016, 53(1): 101-114.

[20] ZARGHAM S, WARD T H, RAMLI R, et al. Topology optimization: A review for structural designs under vibration problems[J]. Structural and Multidisciplinary Optimization, 2016, 53(6): 1157-1177.

[21] THOMSEN J. Topology optimization of structures composed of one or two materials[J]. Journal of Structural Optimization, 1992, 5(1-2): 108-115.

[22] SIGMUND O, TORQUATO S. Design of materials with extreme thermal expansion using a three-phase topology optimization method[J]. Journal of Mechanics and Physics of Solids, 1997, 45(6): 1037-1067.

[23] GIBIANSKY L V, SIGMUND O. Multiphase composites with extremal bulk modulus[J]. Journal of the Mechanics and Physics of Solids, 2000, 48(3): 461-498.

[24] WANG M Y, WANG X. “Color” level sets: A multi-phase method for structural topology optimization with multiple materials[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(6): 469-496.

[25] ZHOU S W, WANG M Y. Multimaterial structural topology optimization with a generalized Cahn-Hilliard model of multiphase transition[J]. Structural and Multidisciplinary Optimization, 2007, 33(2): 89-111.

[26] HUANG X, XIE Y M. Bi-directional evolutionary topology optimization of continuum structures with one or multiple materials[J]. Computational Mechanics, 2009, 43(3): 393-401.

[27] YIN L, ANANTHASURESH G K. Topology of compliant mechanisms with multiple material using a peak function material interpolation scheme[J]. Structural and Multidisciplinary Optimization, 2001, 23(1): 49-62.

[28] GAO T, ZHANG W. A mass constraint formulation for structural topology optimization with multiphase materials[J]. International Journal for Numerical Methods in Engineering, 2011, 88(8): 774-796.

[29] GAO T, XU P, ZHANG W. Topology optimization of thermo-elastic structures with multiple materials under mass constraint[J]. Computers and Structures, 2016, 173: 150-160.

[30] TAKAKOLI R, MOHSENI S M. Alternating active-phase algorithm for multimaterial topology optimization problems: A 115-line MATLAB implementation[J]. Structural and Multidisciplinary Optimization, 2014, 49(4): 621-642.

[31] ZUO W, SAITOU K. Multi-material topology optimization using ordered SIMP interpolation[J]. Structural and Multidisciplinary Optimization, DOI: 10.1007/s00158-016-1513-3.

[32] 隋允康. 建模·变换·优化——结构综合方法新进展[M]. 大连：大连理工大学出版社，1996: 87-195.

SUI Y K. Modelling, transformation and optimization—New developments of structural synthesis method[M]. Dalian: Dalian University of Technology Press, 1996: 87-195 (in Chinese).

[33] 隋允康, 叶红玲, 杜家政. 结构拓扑优化的发展及其模型转化为独立层次的迫切性[J]. 工程力学, 2005, 22(增): 107-118.

SUI Y K, YE H L, DU J Z. Development of structural topological optimization and imminency of its model transformation into independent level[J]. Engineering Mechanics, 2005, 22(Sup): 107-118 (in Chinese).

[34] 隋允康, 叶红玲. 连续体结构拓扑优化的ICM方法[M]. 北京： 科学出版社， 2013: 27-222.

SUI Y J, YE H L. Continuum topology optimization methods ICM[M]. Beijing: Science Press, 2013: 27-222 (in Chinese).

[35] PEDERSEN N L. Maximization of eigenvalues using topology optimization[J]. Structural and Multidisciplinary Optimization, 2000, 20(1): 2-11.

[36] HUANG X, ZUO Z H, XIE Y M. Evolutionary topological optimization of vibrating continuum structures for natural frequencies[J]. Computer & Structures, 2010, 88(5): 357-364.

[37] 彭细荣, 隋允康. 有频率禁区的连续体结构拓扑优化[J]. 固体力学学报, 2007, 28(2): 145-150.

PENG X R, SUI Y K. Topological optimization of the continuum structure with non-frequency-band constraints[J]. Acta Mechanica Solida Sinica, 2007, 28(2): 145-150 (in Chinese).

[38] 彭细荣, 隋允康. 用ICM法拓扑优化静位移及频率约束下连续体结构[J]. 计算力学学报, 2006, 23(4): 391-396.

PENG X R, SUI Y K. Topological optimization of continuum structure with static displacement and frequency constraints by ICM method[J]. Chinese Journal of Computational Mechanics, 2006, 23(4): 391-396 (in Chinese).

[39] SUI Y, PENG X. The ICM method with objective function transformed by variable discrete condition for continuum structure[J]. Acta Mechanica Sinica, 2006, 22(1): 68-75.

[40] YE H L, WANG W W, CHEN N, et al. Plate/shell topological optimization subjected to linear buckling constraints by adopting composite exponential filtering function[J]. Acta Mechanica Sinica, 2016, 32(4): 649-658.

[41] DIAZ A, SIGMUND O. Checkerboard patterns in layout optimization[J]. Structural Optimization, 1995, 10(1): 40-45.

[42] SIGMUND O, PETERSSON J. Numerical instabilities in topology optimization:A survey on procedures dealing with checkerboards, mesh-dependencies and local minima[J]. Structural Optimization, 1998, 16(1): 68-75.

[43] LAZAROV B S, SIGMUND O. Filters in topology optimization based on Helmholtz-type differential equations[J]. International Journal for numerical Methods in Engineering, 2011, 86(6): 765-781.

Lightweightdesignmethodforcontinuumstructureundervibrationusingmultiphasematerials

LONGKai1,2，*,GUXianguang3,WANGXuan4

1.BeijingKeyLaboratoryofEnergySafetyandCleanUtilization,NorthChinaElectricPowerUniversity,Beijing102206,China2.StateKeyLaboratoryforAlternateElectricalPowerSystemwithRenewableEnergySources,NorthChinaElectricPowerUniversity,Beijing102206,China3.SchoolofAutomobileandTrafficEngineering,HefeiUniversityofTechnology,Hefei230009,China4.StateKeyLaboratoryofStructuralAnalysisforIndustrialEquipment,DalianUniversityofTechnology,Dalian116024,China

Toachievelightdesignofcontinuumstructurecontainingmultiphasematerials,atopologicaloptimizationmodelforweightminimizationwiththegiveneigenvalueconstraintisproposedusingtheindependentcontinuousmappingmethod.Twosetsofindependenttopologicalvariablesareemployedtointerpolatetheelementalstiffnessmatrix,themassmatrixandweight.Thesensitivityexpressionsfortheeigenvalueandtotalweightarederived.Theapproximationsoftheeigenvalueandtotalweightcanbeobtainedviathefirst-orderandsecond-orderTaylorexpansion.Thefilteringtechniqueforthefirsttermoftheconstraintfunctionisadoptedasasolutiontothepartialdifferentialequation.Thenumericalinstabilitiesincludingcheckerboardpatternsandmeshdependenceareremoved.Thefeasibilityandsuperiorityoftheproposedmethodarevalidatedbytwo-dimensionalnumericalexamples.Theresultsshowthattheweightoftheoptimalstructureconstructedbymultiphasematerialsislighterthanthatcomposedofconstituentphase.Themodeswitchcanbepreventedbyimposingtheconstraintonthegapoftheadjacentfrequencyoradditionalhighorderfrequencyconstraint.

topologyoptimization;independentcontinuousmappingmethod;continuumstructure;naturalfrequency;modeanalysis

2016-12-05；Revised2017-02-16；Accepted2017-04-25;Publishedonline2017-05-310942

URL：http://hkxb.buaa.edu.cn/CN/html/20171013.html

s：NationalNaturalScienceFoundationofChina(51405123);FundamentalResearchFundsfortheCentralUniversity(2017MS077)

.E-maillongkai1978@163.com

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.221022

V414.5；O343.1

A

1000-6893(2017)10-221022-10

2016-12-05；退修日期2017-02-16；录用日期2017-04-25；< class="emphasis_bold">网络出版时间

时间：2017-05-310942

http://hkxb.buaa.edu.cn/CN/html/20171013.html

国家自然科学基金(51405123)； 中央高校基本科研业务费专项资金(2017MS077)

*

.E-maillongkai1978@163.com

龙凯, 谷先广, 王选. 基于多相材料的连续体结构动态轻量化设计方法J. 航空学报，2017,38(10):221022.LONGK,GUXG,WANGX.LightweightdesignmethodforcontinuumstructureundervibrationusingmultiphasematerialsJ.ActaAeronau-ticaetAstronauticaSinica,2017,38(10):221022.

(责任编辑：徐晓)