湿热环境下复合材料层合板振动与声辐射特性分析

赵天，杨智春，田玮，陈兆林

西北工业大学 航空学院，西安 710072

湿热环境下复合材料层合板振动与声辐射特性分析

赵天，杨智春*，田玮，陈兆林

西北工业大学 航空学院，西安 710072

研究了湿热环境中正交各向异性复合材料层合板结构受简谐激励作用的振动和声辐射特性。考虑了湿热应力和质量效应，利用一阶剪切变形理论和模态叠加法推导出四边简支层合壁板的固有频率计算公式，并采用Rayleigh积分得到其在简谐激励下的声辐射特性公式。基于湿热膨胀的等效性获得不同湿热环境下复合材料层合板的等效热膨胀系数,并进行有限元数值模拟，对理论公式进行了验证。算例结果表明，湿热环境导致复合材料层合板产生湿热应力，使得固有频率减小；单层板的振动特性对湿度和温度的变化更敏感；随着湿度和温度的增加，简谐激励作用下的复合材料层合板的振动速度响应、辐射声压级(SPL)、辐射声功率和声辐射效率曲线的波峰逐渐向低频方向移动，同时声辐射效率随之降低；低阶固有频率受湿度和温度的影响更加明显，声辐射特性曲线中低阶模态的波峰移动更显著。

复合材料层合板；湿热环境；正交各向异性；振动；声辐射

温度和湿度是影响复合材料结构性能的2个重要的环境因素，实际工程应用中经常出现在复合材料层合板结构的寿命周期中经历剧烈湿热变化的情况。树脂基碳纤维复合材料的基体会因为水分的吸收和温度的改变而发生所谓的湿热膨胀并产生湿热应变[1]，引起复合材料结构内部的压缩应力。由于树脂基体比纤维材料对湿热环境更加敏感，在各向异性复合材料中，横向的湿热变形通常比纵向的湿热变形大得多，从而表现出湿热效应的各向异性。正交各向异性复合材料湿热效应产生的附加应力会使复合材料层合壁板结构的振动特性发生改变，进而引起其声辐射特性的变化。

很多学者对复合材料板的振动特性和声辐射特性进行了大量的研究。Shen等[2]讨论了弹性基础上Reissner-Mindlin板在温度载荷和横向动力载荷作用下的动力响应问题。Liew等[3]采用一阶剪切变形理论对复合材料层合板的自由振动特性进行了分析研究。Shooshtari和Razavi[4]也利用了一阶剪切变形理论推出复合材料板的线性振动和非线性振动的理论解。Jeyaraj等[5-6]将有限元和边界元方法结合起来，对正交各向同性板和复合材料板在均匀温升下的振动和声辐射特性进行了研究。Geng等[7-8]采用解析法对均匀热环境下四边简支各向同性板在简谐激励下的声振响应进行了研究，结果表明板的固有频率随温度的增加而降低。同时，对均匀热环境下四边简支各向同性板的振动和声辐射特性进行了试验研究，利用数值模拟进行了对比验证。Li W和Li Y M[9]理论分析了热应力对各向同性层合板的振动和声辐射特性的影响。Geng和Li[10]利用商业有限元软件对四边简支各向同性板在热环境下受简谐激励的振动和声辐射特性进行了研究。应用分段低阶剪切变形理论，Li和Yu[11]对在高温环境下面板为正交各向异性板的夹层板的振动和声辐射特性进行了理论分析。Ram和Sinha[12]采用有限元方法分别研究了温度和湿度对复合材料层合板自由振动的影响。Natarajan等[13]利用扩展有限元的方法研究了湿热环境对板自由振动以及中间有开口层合板的屈曲特性。Zhao等[14]研究了湿度对四边简支条件下正交各向异性板声振特性的影响。Li等[15-18]对复合材料旋转薄壁梁在湿热环境下的自由振动特性进行了研究，并且同时考虑了湿热环境和旋转运动对复合材料薄壁梁动态特性的影响。

综上可知，同时考虑湿热因素影响的复合材料层合板振动和声辐射特性的研究还不多见；分析更具有实际工程意义的正交各向异性复合材料层合板结构受湿热应力作用的动态响应特性和声辐射特性的影响也很少。本文针对四边简支正交各向异性复合材料层合壁板在湿热环境下的振动和声辐射特性开展研究，分析了湿热环境对复合材料层合板固有频率的影响，同时分析了温度和吸湿量的变化对复合材料层合板辐射声压级(SPL)特性、辐射声功率特性和声辐射效率的影响。

1 数学模型

考虑一个由N个不同方向铺层单层板组成的矩形复合材料层合壁板，所有的单层板都是正交各向异性，板周围为无限大刚性障板。如图1所示，板的长和宽分别为a和b,板内吸附了均匀水分，且在(x0,y0)点处受到集中力q(t)的作用。

1.1 复合材料层合板的湿热本构关系

如图1所示，基于一阶剪切变形理论，采用基于拉格朗日描述法的工程坐标系Oxyz，并设坐标轴方向的位移函数为u、v、w，将层合板内部位移场的求解转化到中性面位移场上求解。

(1)

式中：u0、v0、w0为中性面位移；θy和θx为板中性面分别绕x轴和y轴的转角。

假定层合板的温度和湿度都是均匀分布的，且层合板由一种平衡状态变化到另一种平衡状态，只考虑由温度和湿度变化引起的湿热应变。当层合板受湿热作用时，层合板中将产生湿热应变。复合材料热膨胀系数α定义为：单位温度升高引起的层合板纵向和横向长度尺寸改变量(单位为1/℃或1/K)；复合材料湿膨胀系数β定义为：单位吸湿量(1%吸水增重)引起的层合板纵向和横向长度改变量；材料的吸湿量C定义为：吸湿后增加的质量与材料烘干质量之比。温度变化量定义为ΔT=T-T0，T为当前温度，T0为初始温度。则层合板的湿热应变为

(2)

式中：αx、αy和αxy为偏轴坐标系x、y方向的热膨胀系数和热角变系数;βx、βy和βxy为偏轴坐标系x、y方向的湿膨胀系数和湿角变系数。

(3)

式中：

(4)

(5)

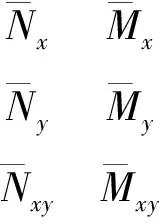
(6)

(7)

考虑横向剪切应力Qx和Qy，其为

(8)

1.2 湿热环境下复合材料层合板的振动方程

当壁板受到简谐激励作用时，利用Hamilton原理推导出考虑湿热应力的复合材料层合板在湿热环境下的运动方程[5]为

(9)

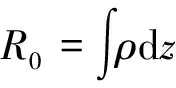
为了得到含湿热应力的板振动响应，将四边简支层合板的振动方程写成其各阶模态叠加的形式，即

(10)

将式(2)、式(3)和式(8)代入到式(9)中，整理可得

(11)

式中：

(12)

令detH=0，可以得到不同湿热环境下层合板的固有圆频率ωm n。同时，当ω11=0时，令detH=0，可以解出层合板的等效临界屈曲温升ΔTcr。假设板受到q(t)为简谐激振力作用，则层合板的横向振动位移可以表示为

(13)

简谐激振力q(t)为

q(t)=q0δ(x-x0,y-y0)ejω t

(14)

式中：ω为激振力的圆频率；q0为激振力的幅值；(x0,y0)为激振点的坐标；m和n为模态因子；Wm n(x,y)为简支板的振型函数；Tm n(t)=ejωm nt。 考虑到模态的正交性，可以将振动方程化为

(15)

式中：

Mm n=∬[(Um nUr s+Vm nVr s+Wm nWr s)R0+

(16)

Qm n=∬qWm ndxdy

(17)

其中：

因此，在湿热环境中各向异性层合板的振动位移可以表示为

(18)

在简谐激振力作用下，层合板的振动速度为

(19)

(20)

1.3湿热环境下复合材料壁板的远场声辐射

基于Rayleigh积分，远场点P(xP,yP,zP)的声压可写为[19]

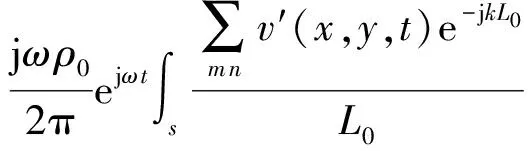
(21)

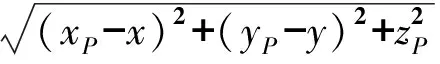
时间平均的辐射声功率可以通过对层合板的表面声压p(x,y,0,t)和振动速度v′(x,y,t)的乘积的积分获得，则辐射声功率可以表示为

(22)

2 壁板声辐射的数值模拟方法

图2为考虑湿热因素的数值分析流程图，对不同温度、均匀湿度分布下的正交各向异性复合材料层合板在简谐激励下的振动和声辐射特性开展研究。使用商业有限元软件MSC.Nastran模拟结构中的湿热扩散并进行板的动态响应计算，同时采用商业软件VA One来进行声辐射计算，并与理论解的结果进行对比验证。

图2 数值分析流程图Fig.2 Flow chart of numerical analysis

2.1湿热膨胀的等效

对于温度和湿度的扩散可以用Fick定律[20]来描述。根据吸湿理论，得到湿扩散方程为

(23)

式中：D为湿扩散常数；t为时间。

热传导微分方程为

(24)

式中：K为热传导率。

对比式(23)与式(24)，发现其数学形式相似，即温度场与湿度场相似，温度场中任意一个节点的温度对应于湿度场中任意一个节点的湿度。湿热膨胀引起的湿应变和热应变为

βy

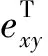
(25)

2.2层合板湿热振动特性

由于有限元软件MSC.Patran/Nastran本身没有湿膨胀模块，为了同时考虑湿热的影响，利用湿热膨胀等效方法和热分析模块对湿热环境下四边简支的碳纤维/环氧树脂基复合材料矩形层合板进行模态分析。计算时，四边简支复合材料层合板的有限元模型用四节点四边形壳单元进行离散，并在正式计算前进行了有限元网格划分的检验，图3所示为温度为60℃、吸湿量为0.57%时，用不同网格密度计算得到的复合材料层合板固有频率。其中，括号中数字表示振型的模态因子。可以看到，当网格密度取为32×32时，计算结果收敛。因此后续计算的网格密度取为32×32。

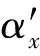
图3 有限元模型固有频率计算收敛性分析Fig.3 Convergence analysis for natural frequencies of finite element model

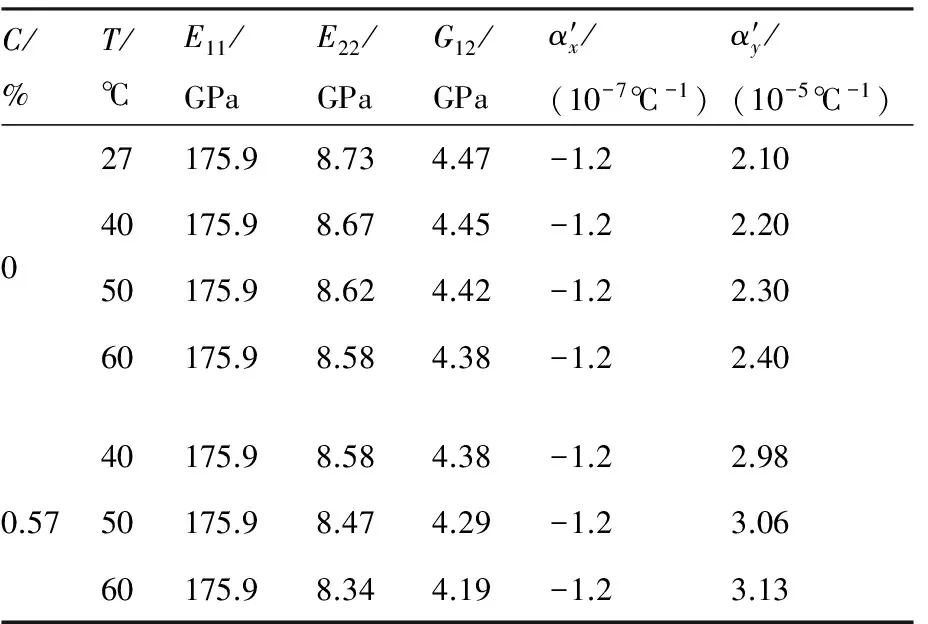
表1 碳纤维-环氧树脂层合板材料参数

利用w11=0以及detH=0得出在厚度同样为3 mm的情况下，单层板和层合板的等效临界屈曲温升为30.7和47.7 ℃，本文中的等效热负载都设定为小于等效临界屈曲热负载。为了考察湿和热2个因素对结构固有频率和模态的影响，定义初始温度T0为标准状态下的温度27 ℃，C=0% 表示的是烘干状态下层合板的吸湿量。分别对烘干状态和吸湿量为0.57%这2种情况下，不同温度下的正交各向异性复合材料层合板进行研究。根据表1，材料横向的弹性模量E22随着温度和湿度的增大而减小，但量值变化不大。表2为正交各向异性层合板前5阶固有振动的理论解和数值解的对比。理论解和数值解的误差定义为(|ft-fN|/ft)×100%，其中ft和fN分别为固有频率的理论解和数值解。从表2可以看出，理论解和数值解吻合较好。

表2 不同湿热条件下理论解与数值解的固有频率对比

2.3 层合板的声辐射特性

如图4所示，使用声学有限元软件VA One中的有限元/边界元(FEM/BEM)模块对所建立的湿热环境下四边简支的复合材料层合壁板模型进行计算。

图4 复合材料层合板有限元/边界元模型Fig.4 FEM/BEM model of composite laminated plate

图5 复合材料层合板在激励点处的速度响应Fig.5 Velocity response at excitation point of composite laminated plate

图6 复合材料层合板辐射声压级(SPL)Fig.6 Radiation Sound Pressure Level (SPL) of composite laminated plate

图5和图6分别为温度为50 ℃、吸湿量为0.57%时复合材料层合板在激励点处的速度响应和在激励点正上方4 m处声压级的理论解与数值解对比。可以看出，考虑湿热的影响，复合材料层合板的速度响应曲线和辐射声压曲线的理论解和数值解在整个频率内吻合良好。

3 结果分析

3.1 湿热环境对振动特性的影响

图7表示正交各向异性复合材料单层板在不同温度T下的固有频率。图8中，实线和虚线分别表示烘干状态下和吸湿量为0.57%条件下的正交各向异性复合材料层合板在不同温度下的固有频率。随着温度和湿度的增加，壁板结构的前5阶固有频率下降，但是各阶振型基本不变。单层板和层合板具有相同的尺寸和材料参数，对比图7和图8可以看出随着温度的升高，单层板对温度更敏感，其固有频率降低得快。同时，低阶固有频率对温升更敏感，其斜率随着温升增加而增加，当接近临界屈曲温升时，固有频率接近为零。从图8中也可以看出，温度和湿度共同作用的影响比单一的温度或吸湿量增加的影响大。

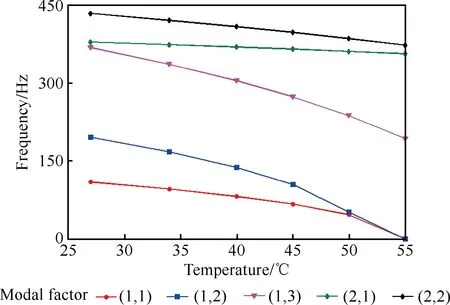
图7 温度对复合材料单层板固有频率的影响Fig.7 Effects of temperature on natural frequencies of composite single lamina

这是因为湿热环境会使树脂基体通过扩散作用吸收水分，使树脂基体软化，削弱基体对碳纤维的支撑能力，降低传递剪切载荷的能力，引起复合材料结构层间剪切强度的降低。对于层合板，如果各单层相互没有粘结，处于自由状态时，温度变化或吸湿后均会产生自由湿热应变。但是单层实际上是相互粘结成一体，只可能产生和层合板变形相协调一致的变形。由层合板的湿热中面应变和曲率确定的各单层湿热应变，显然不等于单层的湿热自由应变，两者之差即单层的残余应变。而这种残余应变和残余应力，最终导致层合板刚度的变化，使得各阶固有频率减小。

3.2 湿热环境对声辐射特性的影响

图9(a)和图9(b)分别表示在烘干状态和吸湿量为0.57%时，不同温度下的复合材料层合板在激励点处的振动速度。从图中可以看出，速度曲线在共振频率处的峰值随着温度的升高而略微降低。在2种条件下，随着温度的升高板的整体刚度减小，从而固有频率减小，使得速度曲线波峰向低频方向漂移。对比图9(a)和图9(b)，也可看出吸湿后的层合板比干燥时固有频率减小，速度曲线波峰向低频方向漂移。同时，速度曲线在各阶固有频率处的幅值随着温度的升高而略微下降。

图10(a)和图10(b)分别表示烘干状态和吸湿量为0.57%条件下，板的激励点正上方4 m处，不同温度下复合材料壁板的辐射声压级曲线。可以看出，随着温度的增加，固有频率减小，因此声压级曲线波峰在1～1 000 Hz的频率范围内向低频方向移动。对比图10(a)和图10(b)，可以看出随着含湿量的增大，声压级曲线波峰也在1～1 000 Hz频率范围内向低频方向漂移。同时，在不同温度和吸湿量的条件下，声压级曲线在第1阶模态(1,1)的共振频率处达到了最大值，在第3阶模态(1,3)的共振频率处峰值也比较明显。这是由于不同模态振型的声辐射效率是不同的，一般来说，偶次阶模态辐射的远场声压相互抵消，声辐射效率低，奇次阶模态的声辐射效率较高。而最终板的辐射声压是由各个模态的辐射声压叠加所得，因此声压级曲线在第1阶模态和第3阶模态的共振频率处的峰值较为明显。

图10 不同湿热环境下复合材料层合板的声压级Fig.10 SPL of composite laminated plate in different hygrothermal environment

图11(a)和图11(b)分别表示在烘干状态和吸湿量为0.57%时，不同温度下层合板的辐射声功率曲线。可以看出，随着温度和吸湿量的升高，辐射声功率曲线波峰在1～1 000 Hz的范围内向低频方向漂移。同时，辐射声压级曲线以及辐射声功率曲线的幅值不随温度和湿度的变化而变化。图12表示在吸湿量为0.57%时，不同温度下层合板的声辐射效率曲线。随着温度的升高，层合板的声辐射效率减小并向低频方向移动。

图11 不同湿热环境下层合板的辐射声功率Fig.11 Sound power of composite laminated plate in different hygrothermal environment

图12 吸湿量为0.57%时不同温度下层合板声辐射效率Fig.12 Sound radiation efficiency of composite laminated plate with 0.57% moisture content under different temperatures

4 结 论

1) 随着温度的升高和吸湿量的增大，正交各向异性复合材料层合板的湿热应力增大，整体刚度减小，导致固有频率减小，模态振型基本保持不变。单层板比层合板对温度的变化更敏感，其固有频率降低得更快。湿热因素同时作用比单一温度或湿度作用的影响大。

2) 在本文研究的温度和吸湿量变化范围内，随着温度的升高，振动速度曲线在各阶共振频率处的幅值略微下降；但辐射声压级曲线以及辐射声功率曲线的幅值基本不随温度和湿度的变化而变化。

3) 随着温度和湿度的增加，速度响应曲线、辐射声压级曲线以及辐射声功率曲线的波峰在1～1 000 Hz的频率范围内向低频方向漂移，这是由于复合材料层合板固有频率降低导致的。低阶固有频率对湿热的影响更敏感，因此声辐射特性曲线低阶共振频率峰值漂移得更明显。同时，随着温度的升高，层合板的声辐射效率减小并向低频方向移动。

4) 由于不同模态振型的声辐射效率不同，不同湿热条件下声压级曲线在各阶共振频率处的幅值所受的影响也不同，在第1阶模态和第3阶模态的共振频率处的峰值变化较大。

[1] 郑建军. 湿热环境对复合材料剪切层合板自由振动和动力响应的影响[D]. 上海: 上海交通大学, 2002: 21-24.

ZHENG J J. Hygrothermal effects on the vibration and transient response of shear deformed laminated plates[D]. Shanghai: Shanghai Jiaotong University, 2002: 21-24 (in Chinese).

[2] SHEN H S, YANG J, ZHANG L. Dynamic response of Reissner-Mindlin plates under thermomechanical loading and resting on elastic foundations[J]. Journal of Sound and Vibration, 2000, 232(2): 309-329.

[3] LIEW K M, HUANG Y Q, REDDY J N. Vibration analysis of symmetrically laminated plates based on FSDT using the moving least squares differential quadrature method[J]. Computer Methods in Applied Mechanics and Engineering, 2003, 192(19): 2203-2222.

[4] SHOOSHTARI A, RAZAVI S. A closed form solution for linear and nonlinear free vibrations of composite and fiber metal laminated rectangular plates[J]. Composite Structures, 2010, 92(11): 2663-2675.

[5] JEYARAJ P, GANESAN N, PADMANABHAN C. Vibration and acoustic response of a composite plate with inherent material damping in a thermal environment[J]. Journal of Sound and Vibration, 2009, 320(1-2): 322-338.

[6] JEYARAJ P, PADMANABHAN C, GANESAN N. Vibration and acoustic response of an isotropic plate in a thermal environment[J]. Journal of Vibration and Acoustics, 2008, 130(5): 301-306.

[7] GENG Q, LI Y M. Analysis of dynamic and acoustic radiation characters for a flat plate under thermal environments[J]. International Journal of Applied Mechanics, 2012, 4(3): 1250028.

[8] GENG Q, LI H, LI Y M. Dynamic and acoustic response of a clamped rectangular plate in thermal environments: Experiment and numerical simulation[J]. Journal of the Acoustical Society of America, 2014, 135(5): 2674-2682.

[9] LI W, LI Y M. Vibration and sound radiation of an asymmetric laminated plate in thermal environments[J]. Acta Mechanica Solida Sinica, 2005, 28(1): 11-22.

[10] GENG Q, LI Y M. Solutions of dynamic and acoustic responses of a clamped rectangular plate in thermal environments[J]. Journal of Vibration and Control, 2016, 22(6): 1593-1603.

[11] LI X Y, YU K P. Vibration and acoustic responses of composite and sandwich panels under thermal environment[J]. Composite Structures, 2015, 131: 1040-1049.

[12] RAM K S S, SINHA P K. Hygrothermal effects on the free vibration of laminated composite plates[J]. Journal of Sound and Vibration, 1992, 158(1): 133-148.

[13] NATARAJAN S, DEOGEKAR P S, MANICKAM G, et al. Hygrothermal effects on the free vibration and buckling of laminated composites with cutouts[J]. Composite Structures, 2014, 108: 848-855.

[14] ZHAO X, GENG Q, LI Y M. Vibration and acoustic response of an orthotropic composite laminated plate in a hygroscopic environment[J]. Journal of the Acoustical Society of America, 2013, 133(3): 1433-1442.

[15] LI X, LI Y H, QIN Y. Free vibration characteristics of a spinning composite thin-walled beam under hygrothermal environment[J]. International Journal of Mechanical Sciences, 2016, 119: 253-265.

[16] JIANG B K, XU J, LI Y H. Flapwise vibration analysis of a rotating composite beam under hygrothermal environment[J]. Composite Structures, 2014, 117: 201-211.

[17] QIN Y, LI X, YANG E C, et al. Flapwise free vibration characteristics of a rotating composite thin-walled beam under aerodynamic force and hygrothermal environment[J]. Composite Structures, 2016, 153: 490-503.

[18] QIN Y, LI Y H. Influences of hygrothermal environment and installation mode on vibration characteristics of a rotating laminated composite beam[J]. Mechanical Systems and Signal Processing, 2017, 91: 23-40.

[19] FAHY F, KALNINS A. Sound and structural vibration radiation, transmission, and response by Frank Fahy[J]. The Journal of the Acoustical Society of America, 1987, 81(5): 1651- 1651.

[20] FICK A V. On liquid diffusion[J]. Philosophical Magazine Series 4, 1855, 10(63): 30-39.

Vibrationandacousticradiationcharacteristicsanalysisofcompositelaminatedplateinhygrothermalenvironments

ZHAOTian，YANGZhichun*,TIANWei,CHENZhaolin

SchoolofAeronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China

Thevibrationandacousticradiationcharacteristicsofanorthotropiccompositelaminatedplateexcitedbyaharmonicconcentratedforceinhygrothermalenvironmentsarestudied.Takingtheeffectsofhygrothermalstressandadditionalmasseffectintoaccount,wederivethenaturalfrequencyformulationsoffour-edgesimply-supportedlaminatedpanelbasedonthefirst-ordersheardeformationtheoryandmodesuperpositionapproach.ThesoundradiationformulationsforthepanelareobtainedbyusingRayleighintegral.Furthermore,theequivalentcoefficientsofthermalexpansionofthepanelinthehygrothermalenvironmentareobtainedaccordingtotheequivalenceofhygrothermalexpansionandthermalexpansion.Numericalsimulationsarecarriedoutwiththefiniteelementmethodtoverifytheanalyticalsolutions.Itisobservedthatthenaturalfrequenciesdecreasewiththeincreaseofmoisturecontentandtemperatureduetotheeffectofhygrothermalstress.Theorthotropiclaminaismoresensitivetohygrothermaleffectthanthelaminatedplate.Meanwhile,thepeaksofdynamicresponse,SoundPressureLevel(SPL),soundpowerandacousticradiationefficiencycurvesofthepanelgenerallyshifttowardslowerfrequencies;andtheacousticradiationefficiencydecreaseswiththeelevationoftemperatureandmoisturecontent,andthisphenomenonismoreevidentinthelowfrequencyregion.

compositelaminatedplate;hygrothermalenvironment;orthotropic;vibration;acousticradiation

2016-12-09；Revised2017-01-22；Accepted2017-03-29;Publishedonline2017-04-191331

URL：http://hkxb.buaa.edu.cn/CN/html/20171014.html

NationalNaturalScienceFoundationofChina(11472216)

.E-mailyangzc@nwpu.edu.cn

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.221038

V215.3

A

1000-6893(2017)10-221038-11

2016-12-09；退修日期2017-01-22；录用日期2017-03-29；< class="emphasis_bold">网络出版时间

时间：2017-04-191331

http://hkxb.buaa.edu.cn/CN/html/20171014.html

国家自然科学基金(11472216)

*

.E-mailyangzc@nwpu.edu.cn

赵天，杨智春, 田玮， 等. 湿热环境下复合材料层合板振动与声辐射特性分析J． 航空学报,2017,38(10):221038.ZHAOT，YANGZC，TIANW,etal.VibrationandacousticradiationcharacteristicsanalysisofcompositelaminatedplateinhygrothermalenvironmentsJ.ActaAeronauticaetAstronauticaSinica，2017,38(10):221038.

(责任编辑：徐晓)