考虑输入饱和的制导控制一体化设计
王松艳,孙向宇,杨胜江,晁涛,*
1.哈尔滨工业大学 控制与仿真中心,哈尔滨 150080 2.北京空天技术研究所,北京 100074
考虑输入饱和的制导控制一体化设计
王松艳1,孙向宇1,杨胜江2,晁涛1,*
1.哈尔滨工业大学 控制与仿真中心,哈尔滨 150080 2.北京空天技术研究所,北京 100074
高超声速飞行器俯冲时具有快时变特性,执行机构限于物理约束极易导致控制输入达到饱和,针对该问题提出考虑输入饱和约束的制导与控制一体化设计方法。首先,建立纵向制导与控制一体化设计模型,采用干扰观测器对系统不确定性进行估计补偿,然后结合加幂积分方法与嵌套饱和方法设计了新的制导控制一体化非线性控制律。通过严格的理论分析证明了带有饱和约束的控制器可令系统状态全局有限时间稳定,由于控制律中的虚拟控制量均考虑了饱和约束,做到了全局协调抗饱和,从而可更充分地利用飞行器控制能力去实现精准控制。数值仿真实例验证了提出方法的有效性及鲁棒性。
高超声速飞行器;连续有限时间;输入饱和;制导控制一体化;级联系统
近空间高超声速飞行器在军用和民用方面均具有广阔的应用前景,在情报收集、通讯保障、侦查监视等方面具有独特的优势[1]。然而对该类飞行器的制导控制系统进行设计极具挑战,它是一类高动态、强耦合、快时变、不确定、带约束的多变量系统,而且其自身动力学特性复杂,因此在未知的飞行环境和较高的控制要求下,设计兼具鲁棒性和适应性的制导与控制方法具有较高难度[2]。将制导与控制系统进行一体化设计的策略可以更合理地对飞行器的控制能力进行分配,在很多低速运动对象的控制中收到良好效果,如文献[3-5],近年来这种设计思路在制导控制系统设计领域逐步成为热点。由于将姿态控制回路的影响引入到了制导回路的设计中,有效地减少了过度控制,由此可以改善控制器性能,这种控制策略也给高速运动对象的制导控制系统设计提供了新的解决思路。由于执行机构的物理约束是普遍存在的,快时变过程易导致控制量幅值变大,极易达到执行机构约束上限而导致控制量饱和的现象发生,饱和问题如若被忽视将导致控制性能下降甚至系统崩溃。
将制导与控制系统进行一体化设计的思想起源于20世纪80年代,至今收获了较多的研究成果。其中比较有代表性的如查旭等[6]采用了一种特殊的终端滑模控制面,利用非线性终端滑模控制方法解决了带有非匹配不确定性及未建模动态的一体化设计问题,设计结果保证了系统状态可以在有限时间收敛。Shima等[7]采用滑模控制方法设计了纵向制导控制一体化控制律,值得一提的是,用零控脱靶量作为滑模面,有效地提高了拦截精度。尹永鑫等[8]较早地尝试了三维制导控制一体化设计,将扩张状态观测器与动态逆方法相结合,最终得到较好结果。侯明哲等[9]突破性地考虑了侧滑转弯飞行器三维控制通道间的耦合因素,基于自适应块动态面方法设计了三维制导控制一体化控制器,同时采用自适应方法对不确定上界进行了有效估计补偿,提高了系统的鲁棒性。除此之外,一些新成果[4,10-11]也为制导控制一体化设计思想趋于成熟奠定基础。然而,已有研究成果中多数仅仅得出渐近稳定结论且较少有对系统全局稳定性进行考虑,同时对制导控制一体化设计中存在输入饱和的问题也鲜有深入研究。
考虑输入饱和的控制方法可大概可分为以下几类。第1类是Teel在1992年最早提出,通过建立饱和非线性模型,设计了多种非线性饱和控制器[12]。周彬和段广仁[13]在此方法的基础上,建立了一类新的嵌套类型的饱和控制器,这种方法不仅继承了Teel原有方法的优点,而且改善了闭环系统的动态表现。Sussmann等[14]引入了依赖于状态的饱和函数,后来这个函数又被改进为嵌套形式的饱和函数,文献[15-16]中的改进使闭环系统的收敛速度明显加快。第2类为1993年Lin和Saberi提出了一种低增益控制方法[17],后来文献[18-19]又将其改进为高低增益混合的控制方法来处理带有输入饱和的链式积分系统,得到了半全局稳定控制器。通过对饱和非线性函数的改进,该方法的瞬时性能被进一步提高。第3类为采用光滑函数替换饱和函数,然后利用非线性控制理论设计考虑输入饱和约束的控制律,梁小玲等[20-21]在动态面控制方法的基础上,加入了饱和影响因素并引入执行机构动态模型,设计了飞行器纵向抗饱和制导控制一体化算法。以上针对饱和问题的解决思路,有些是基于线性矩阵不等式,计算效率较低;有些需要对系统进行扩充,增加了设计的复杂性,而饱和函数的近似替换也会引入误差。
本文就制导控制一体化设计中存在控制输入饱和的问题,从全局角度为这类级联系统设计了抗饱和稳定控制方法。基本思路为:设计切换输入饱和控制器,在饱和控制器的作用下,令系统状态在有限时间内收敛至一个由饱和度决定的控制区域中。在该区域中,饱和控制器退化为原来的非饱和递归控制器,在递归控制器的作用下系统状态有限时间稳定到平衡点,从而实现全局有限时间稳定。
1 问题描述
建立飞行器与目标的相对关系,如图1所示。图中:OXY为惯性坐标系;M代表飞行器,T代表目标;Vm和Vt分别为飞行器和目标的机动速度;am与at分别为飞行器与目标的机动加速度;θm与θt分别为飞行器与目标的速度倾角;λD为视线高低角;R为飞行器与目标间的距离。
参照文献[22],建立高超声速飞行器在纵向平面的相对运动模型为
(1)
俯仰通道动力学模型可以描述为
(2)

将式(1)和式(2)综合后转为状态空间的表达形式,式(3)为制导控制一体化设计的纵向平面模型

图1 飞行器与目标相对运动Fig.1 Relative movement between vehicle and target
(3)
式中:

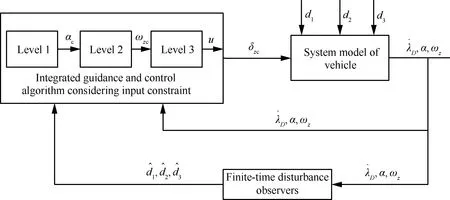
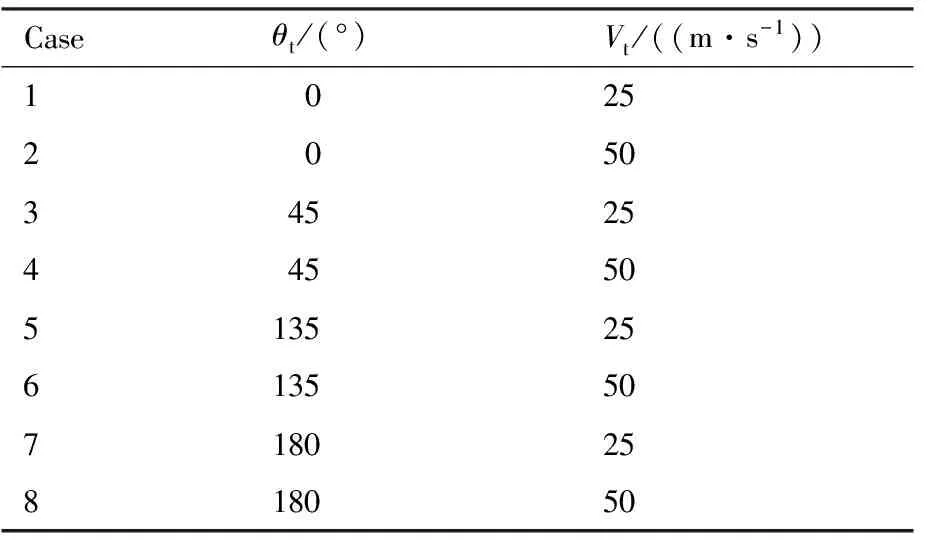
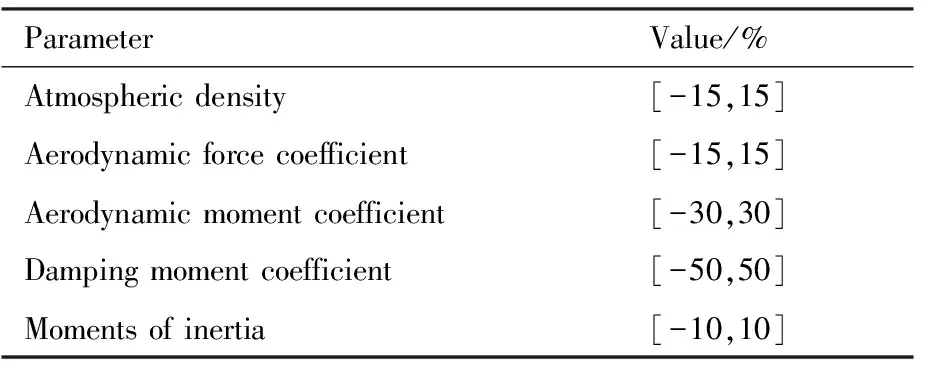
假设1模型中存在的不确定性是有界的,即|di| 本文的设计目的为针对式(3),设计考虑控制量幅值约束的有限时间制导控制一体化控制规律。 首先给出如下引理与假设,辅助证明定理。 引理1[23]有限时间Lyapunov稳定性定理 对于系统,如果存在连续可微函数V,U→R满足: 1)V是正定函数。 2) 存在正实数c>0和α∈(0,1),以及一个包含原点的开邻域U0∈U使得 x∈U0 假设2存在qi≥1(i=1,2,…,n+1),τ∈(0,1)以及光滑函数ρi(x1,x2,…,xi)≥0(i=1,2,…,n)可以使得对于所有x,fi(z,0)=0存在 |fi(x1,x2,…,xi)|≤ρi(·)(|x1|q1/qi+1+ |x2|q2/qi+1+…+|xi|qi/qi+1) 引理2[23]若0 |xp-yp|≤21-p|x-y|p 引理3[23]对于任意x,y∈R,c>0,d>0,及任意的非负实函数γ(x,y),有 引理4[24]若xi∈R(i=1,2,…,n),0 (|x1|+|x2|+…+|xn|)p≤|x1|p+|x2|p…+ |xn|p≤n1-p(|x1|+|x2|+…+|xn|)p 引理5[23]假设x(t)和x*(t)是时间t的连续函数,则有 为可导的正定函数,其中q=q1/q2,q1和q2为互质的正奇数。 2.1 干扰观测器设计 针对设计模型中包含的不确定性di,设计干扰观测器进行补偿。参照文献[25]中干扰观测器的设计并做出相应的改进,对式(3)中不确定性项分别设计干扰观测器进行观测补偿: (4) (5) (6) 由式(3)与式(4)、式(5)、式(6)可以推导得出误差方程通式为 (7) 2.2 全局稳定控制器设计 针对系统设计模型式(3),提出如定理1所示有限时间控制算法,在一定的控制输入饱和约束范围内,可令系统全局有限时间稳定且具有抗饱和控制效果,系统的结构框图如图2所示,图中αc与ωzc分别为α与ωz的期望指令值。 定理1对于制导控制一体化设计模型式(3)设计虚拟控制指令: (8) (9) 可以令原系统状态在有限时间收敛至原点。 证明:定理的证明以原理性证明为主,分为两部分,第1部分先证明系统状态可以在任意初始位置收敛至与饱和度εi相关的区域内,第2部分证明系统状态在非饱和区域内可以有限时间收敛至平衡点。 第1部分,证明系统状态在饱和区域的有限时间收敛特性。 假设存在时刻t1使得当t≥t1时状态Xn满足 (10) 式中:ε为对应多层情况下的饱和度。式(10)及以下含有Xn(t)的公式中: Xn=[x1(t)x2(t) …xn(t)]Tn=2,3,4。 采用反证法证明,首先证明存在时刻t1使得 (11) (12) 由式(12)可得到对于任意时刻t≥0,存在 (13) 定义 (14) 因此,当t≥0时,对式(13)积分可以得到 (15) 结合式(12)和式(15)以及不等式 (16) 图2 系统结构图Fig.2 Structure chart of system 继续证明式(10)成立,依然采用反证法证明,假设该式不成立,那么至少存在时刻t*>t1使得 (17) (18) (19) (20) 或者得到结果 (21) (22) (23) 由式(20)可得 (24) μn的定义同式(14)。对式(24)积分可得 (25) (26) 同理由式(19)可得 (27) 由式(26)和式(27)可以推出 (28) 由式(24)可得xn(t)是随着自变量单调递减的,进而可得 (29) 将式(18)和式(19)代入式(29),可以得出 (30) (31) 引理6如果系统状态满足 (32) (33) 满足 (34) 注1对于式(32),由于飞行器制导控制系统状态具有一定的物理意义,均为有界,因此适当选择饱和度ε与系数ki可以容易满足该式。 由式(30)与引理6可以推导得出 (35) 将式(28)代入式(35)可得 (36) 根据μn的定义可以推导得出 4(1+kn-1)αn-1(·) (37) 由式(36)和式(37)可推出 (38) 出现矛盾。因此情况式(18)~式(20)是不成立的,同理也可证明情况式(21)~式(23)也是不成立的。因此,反证假设不成立,当t>t1时,有 即系统的虚拟控制量在饱和区域内,系统状态可以在有限时间收敛至与饱和度相关的有界范围内。 第2部分,证明系统状态在非饱和区域的有限时间稳定特性。此时定理1中的虚拟控制量表达式中的标准饱和函数可以忽略。假设通过干扰观测器可以精确估计干扰值的真实值。 首先建立Lyapunov函数: (39) 对式(39)求导可以得到 (40) 式中:ξ1=x1。 然后考虑证明系统式(3)的前两个子系统的稳定性,为二阶系统建立如式(41)所示的Lyapunov函数。 V2(x1,x2)=V1(x1)+W2(x1,x2) (41) 式中: 注2由引理5可以得知,函数W2是连续可导且正定的,可辅助衡量二阶系统的稳定性。 对式(41)进行求导可得 (42) 21-1/q2|x1||ξ2|1/q2≤ (43) (44) (45) (46) 又因为 |ξ2|1/q2+(μ1(·)+ρ1(·))|x1|1/q2 (47) 由此可以得出 21-1/q2|ξ2|(|ξ2|1/q2+(μ1(·)+ρ1(·))· |x1|1/q2)≤21-1/q2|ξ2|1+1/q2+21-1/q2(μ1(·)+ρ1(·))|x1|1/q2|ξ2| (48) (49) 其中:m1、m2、m3、m21、m22、m23均为正的系数,且有m22=21-1/q2,m23=m1+m3。 (50) μ2≥m21+m22+m23 (51) 则有 (52) 定义Lyapunov函数 V3=V2+W3(x1,x2,x3) (53) 同理可以推导得出式(54),过程在此不赘述。 (54) 又由 (55) 取ε=(1+τ)/2,m=2-(3+τ)/2,0<ε<1,可得到 (56) 由引理1可知,系统在非饱和区域范围是满足有限时间稳定的。 综上所述,考虑输入存在饱和因素时,定理1给出的控制策略可以令系统状态在任意初始值均能在有限时间稳定至平衡点。 表1 飞行器初始状态Table 1 Initial states of vehicle 3.1 抗饱和与非抗饱和设计方法对比仿真实验 为了验证抗饱和方法的有效性,首先设计对比实验1:将抗饱和加幂积分一体化设计方法(Anti-windup IGC)与非饱和加幂积分一体化设计方法(IGC)进行对比仿真。 抗饱和控制方法的终端精度为1.121 m,常规方法即反步滑模方法得到的终端精度为1.503 m,均满足指标要求且相差不大; 但是通过图3(a)和图3(b)可以明显看出, 抗饱和控制方法可以有效地规避约束,这样控制器可以确保系统在可控范围内。从图3(d)的轨迹曲线可以看出,采用抗饱和控制方法的轨迹曲率更高,增加了轨迹航程,使状态及控制量变化过程更加平缓,便于执行机构的跟踪。通过该组仿真实验还可以看出,由于采用结构相同的控制算法,因此曲线形状近似,但因为控制算法中抗饱和部分的引入,将控制量快变过程转为缓变过程,出现近似滞后效果来避免饱和现象的出现,方法符合实际情况。 图3 实验1情况下的仿真结果Fig.3 Simulation results of experiment 1 3.2 抗饱和与常规方法对比仿真实验 为了揭示抗饱和加幂积分方法的优势,设计对比实验2:采用文献中常用的反步滑模控制制导控制一体化设计方法(BSMC IGC)作为对比对象与本文提出的抗饱和制导控制一体化设计方法进行对比。 统计仿真结果,采用反步滑模方法的终端精度为2.105 m,而基于加幂积分方法的一体化设计方法为1.121 m,加幂积分方法攻击精度更高。通过图4中的仿真曲线可看出应用加幂积分方法处理纵向制导控制一体化设计问题相比反步滑模一体化算法具有一定的优势,可以使系统状态收敛至期望值,在过程状态不饱和的情况下,轨迹变化更快,稳定时间更短,终端精度较高。 图4 实验2情况下的仿真结果Fig.4 Simulation results of experiment 2 3.3 存在外扰情况下仿真实验 为了验证提出的制导控制一体化算法在外扰情况下具有较强的鲁棒性,令目标做小范围机动,设计如表2所示的仿真实验。 目标的小范围机动可以近似为一种不确定外扰因素,目标的速度倾角为45°或135°时视做目标沿该角度做爬坡机动。图5为飞行器在目标进行不同机动情况下的飞行轨迹,统计该组仿真实验的仿真结果可知,飞行器与目标之间的终端距离均满足精度要求且状态量均未达到饱和状态。由该组仿真实验可知本文提出的抗饱和有限时间制导控制一体化控制算法在外扰存在情况下是有效的且具有较强的鲁棒性。 表2 目标机动条件Table 2 Maneuvering condition of target 图5 目标不同机动情况下的飞行器运动轨迹曲线Fig.5 Trajectory curves of vehicle with different maneuvering targets 3.4 存在参数不确定情况下仿真实验 飞行器在飞行过程中存在多种参数摄动,如大气密度、气动力与力矩参数、转动惯量等,对控制器的影响不可忽略。本部分为了验证设计的方法具有良好的鲁棒性,分别对大气密度、气动系数、阻尼系数、转动惯量等参数进行蒙特卡罗仿真实验,拉偏参数幅值范围见表3,仿真实验次数为100。 表3 拉偏参数说明Table 3 Description of parameters deviation 通过数值仿真得到存在参数不确定性情况下的三维轨迹曲线如图6所示。参数存在随机偏差的情况下,终端位置偏差均在10 m以内,满足约束要求,由此说明设计的控制器对参数不确定性具有较好的鲁棒性。 图6 参数拉偏情况下飞行器运动轨迹曲线Fig.6 Trajectory curves of vehicle with parameter deviation 1) 针对制导控制一体化设计模型,控制输入存在饱和的情况下,基于加幂积分的嵌套抗饱和方法是有效的,可以保证虚拟控制量均不饱和并可以实现全局稳定控制。 2) 在保证精确击中目标的前提下,相比反步滑模制导控制一体化设计方法,本文提出的方法收敛速度更快。 3) 存在外部扰动以及系统参数不确定性的情况下,本文提出的方法具有较好的鲁棒性。 此外,将本文提出的方法扩展到三维制导控制一体化设计中,可以作为未来的研究方向。 [1] 孙长银, 穆朝絮, 余瑶. 近空间高超声速飞行器控制的几个科学问题研究[J]. 自动化学报, 2013, 39(11): 1901-1913. SUN C Y, MU C X, YU Y. Some control problems for near space hypersonic vehicles[J]. Acta Automatica Sinica, 2013, 39(11): 1901-1913 (in Chinese). [2] 崔尔杰. 近空间飞行器研究发展现状及关键技术问题[J]. 力学进展, 2009, 39(6): 658-673. CUI E J. Research statutes, development trends and key technical problems of near space flying[J]. Advances in Mechanics, 2009, 39(6): 658-673 (in Chinese). [3] 张金鹏, 周池军, 雷虎民. 基于滑模反演控制方法的纵向制导控制一体化设计[J]. 固体火箭技术, 2013, 36(1): 11-16. ZHANG J P, ZHOU C J, LEI H M. Integrated guidance and control design based on sliding-mode and back-stepping control[J]. Journal of Solid Rocket Technology, 2013, 36(1): 11-16 (in Chinese). [4] 董飞垚, 雷虎民, 李炯, 等. 拦截弹自适应最优滑模制导和控制一体化设计[J]. 宇航学报, 2013, 34(11): 1456-1461. DONG F Y, LEI H M, LI J, et al. Design of integrated adaptive optimal sliding-mode guidance and control for interceptor[J]. Journal of Astronautics, 2013, 34(11): 1456-1461 (in Chinese). [5] 董飞垚, 雷虎民, 周池军, 等. 导弹鲁棒高阶滑模制导控制一体化研究[J]. 航空学报, 2013, 34(9): 2212-2218. DONG F Y, LEI H M, ZHOU C J, et al. Research of integrated robust high order sliding mode guidance and control for missiles[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(9): 2212-2218 (in Chinese). [6] 查旭, 崔平远, 常伯浚. 攻击固定目标的飞行器制导控制一体化设计[J]. 宇航学报, 2005, 26(1): 13-18. ZHA X, CUI P Y, CHANG B J. An integrated approach to guidance and control for aircraft applying to attack the ground fixed targets[J]. Journal of Astronautics, 2005, 26(1): 13-18 (in Chinese). [7] SHIMA T, IDAN M, GOLAN O M. Sliding-mode control for integrated missile autopilot guidance[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(2): 250-260. [8] 尹永鑫, 石文, 杨明. 基于动态逆和状态观测的制导控制一体化设计[J]. 系统工程与电子技术, 2011, 33(6): 1342-1345. YIN Y X, SHI W, YANG M. Integrated guidance and control based on dynamic inverse and extended state observer method[J]. Systems Engineering and Electronics, 2011, 33(6): 1342-1345 (in Chinese). [9] HOU M Z, LIANG X L, DUAN G R. Adaptive block dynamic surface control for integrated missile guidance and autopilot[J]. Chinese Journal of Aeronautics, 2013, 26(3): 741-750. [10] 张尧, 郭杰, 唐胜景, 等. 导弹制导与控制一体化三通道解耦设计方法[J]. 航空学报, 2014, 35(12): 3438-3450. ZHANG Y, GUO J, TANG S J, et al. Integrated missile guidance and control three-channel decoupling design method[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(12): 3438-3450 (in Chinese). [11] 赵国荣, 冯淞琪. 适用于制导控制一体化的模糊滑模方法[J]. 控制与决策, 2014, 29(7): 1321-1324. ZHAO G R, FENG S Q. Fuzzy sliding model method for integrated guidance and control[J]. Control and Decision, 2014, 29(7): 1321-1324 (in Chinese). [12] TEEL. Global stabilization and restricted tracking for multiple integrators with bounded controls[J]. Systems and Control Letters, 1992, 18(3): 165-171. [13] ZHOU B, DUAN G R. A novel nested non-linear feedback law for global stabilization of linear systems with bounded controls[J]. International Journal of Control, 2008, 81(9): 1352-1363. [14] SUSSMANN H J, SONTAG E D, YANG Y. A general result on the stabilization of linear systems using bounded controls[J]. IEEE Transactions on Automatic Control, 1994, 39(12): 2411-2425. [15] MARCHAND N, HABLY A. Global stabilization of multiple integrators with bounded controls[J]. Automatica, 2005, 41(12): 2147-2152. [16] ZHOU B, DUAN G R, HE K. Global stabilization of linear systems with bounded controls using state-dependent saturation functions[J]. Journal of Systems Science and Complexity, 2011, 24: 477-490. [17] LIN Z, SABERI S. Semi-global exponential stabilization of linear systems subject to “input saturation” via linear feedbacks[J]. Systems and Control Letters, 1993, 21(3): 225-239. [18] ZHOU B, DUAN G R. Global stabilization of linear systems via bounded controls[J]. Systems & Control Letters, 2009, 58(1): 54-61. [19] ZHOU B, ZHENG W X, DUAN G R. An improved treatment of saturation nonlinearity with its application to control of systems subject to nested saturation[J]. Automatica, 2011, 47 (1): 306-315. [20] LIANG X L, HOU M Z, DUAN G R. Integrated guidance and control for missile in the presence of input saturation and angular constraints[C]∥IEEE Control Conference. Piscataway, NJ: IEEE Press, 2013: 1070-1075. [21] LIANG X L, HOU M Z, DUAN G R. Adaptive dynamic surface control for integrated missile guidance and autopilot in the presence of input saturation[J]. Journal of Aerospace Engineering, 2015, 28(5): 401-412. [22] YAN H, JI H B. Integrated guidance and control for dual-control missiles based on small gain theorem[J]. Automatica, 2012, 48(1): 2686-2692. [23] QIAN C J, LIN W. A continuous feedback approach to global strong stabilization of nonlinear systems[J]. IEEE Transactions on Automatic Control, 2001, 46(7): 1061-1076. [24] HARDY G H, LITTLEWOOD J E. Inequalities[M]. Cambridge: Cambridge University Press, 1952. [25] 卜祥伟, 吴晓燕, 陈永兴, 等. 基于非线性干扰观测器的高超声速飞行器滑模反演控制[J]. 控制理论与应用, 2014, 31(11): 1473-1479. BU X W, WU X Y, CHEN Y X. Nonlinear disturbance observer based sliding mode backstepping control of hypersonic vehicle[J]. Control Theory and Applications, 2014, 31(11): 1473-1479 (in Chinese). Integratedguidanceandcontroldesignconsideringinputsaturation WANGSongyan1,SUNXiangyu1,YANGShengjiang2,CHAOTao1,* 1.ControlandSimulationCenter,HarbinInstituteofTechnology,Harbin150080,China2.BeijingAerospaceTechnologyInstitute,Beijing100074,China Hypersonicvehicleisfastvaryingindivephase,soitsactuatoriseasytobesaturatedbecauseofthephysicalconstraint.Integratedguidanceandcontrolmethodconsideringinputconstraintisproposed.Thelongitudinaldesignmodelforintegratedguidanceandcontrolisbuilt.Anextendedstateobserveristakentoestimatetheuncertaintiesandcompensatethem.Anewintegratedguidanceandcontrolmethodisbuiltforthecascadedsystembasedonthemethodofaddingapowerintegratorandthemethodofnestedanti-windup.Rigoroustheoreticanalysisprovesthatthecontrolstrategycanresultinexpectedequilibriumofallsystemstatesinfinitetime.Becauseallthevirtualcontrolvariablesconsiderthesaturationrestraint,muchmorecontrolcapacityofthevehiclecanbesavedtorealizeaccuratemanipulation.Anumericalsimulationcaseisadoptedtoverifytheeffectivenessandrobustnessoftheproposedmethod. hypersonicvehicle;continuousfinite-time;inputsaturation;integratedguidanceandcontrol;cascadedsystem 2016-10-28;Revised2016-12-06;Accepted2017-01-05;Publishedonline2017-01-121117 URL:http://hkxb.buaa.edu.cn/CN/html/20171018.html s:NationalNaturalScienceFoundationofChina(61403096);ChinaPostdoctoralScienceFoundation(2014M551242);theFundamentalResearchFundsfortheCentralUniversities(HIT.NSRIF.2014036,HIT.NSRIF.2015036);HeilongjiangPostdoctoralFund(LBH-Z12112) .E-mailchaotao2000@163.com http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn 10.7527/S1000-6893.2017.320897 V448.2 A 1000-6893(2017)10-320897-11 2016-10-28;退修日期2016-12-06;录用日期2017-01-05;< class="emphasis_bold">网络出版时间 时间:2017-01-121117 http://hkxb.buaa.edu.cn/CN/html/20171018.html 国家自然科学基金(61403096); 中国博士后科学基金(2014M551242); 中央高校基本科研业务费专项资金(HIT.NSRIF.2014036,HIT.NSRIF.2015036); 黑龙江省博士后资助经费(LBH-Z12112) * .E-mailchaotao2000@163.com 王松艳,孙向宇,杨胜江,等.考虑输入饱和的制导控制一体化设计J. 航空学报,2017,38(10):320897.WANGSY,SUNXY,YANGSJ,etal.IntegratedguidanceandcontroldesignconsideringinputsaturationJ.ActaAeronauticaetAstro-nauticaSinica,2017,38(10):320897. (责任编辑:张玉, 李世秋)2 制导控制一体化抗饱和控制器设计
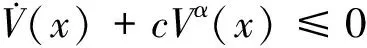
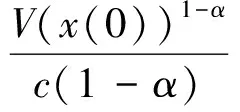
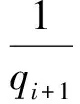


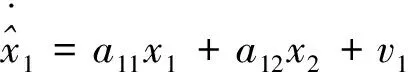
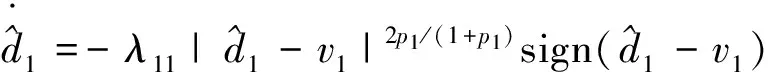
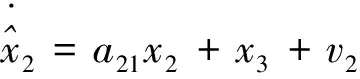


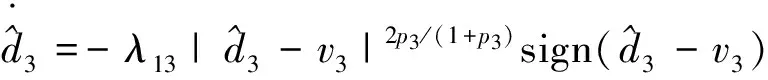

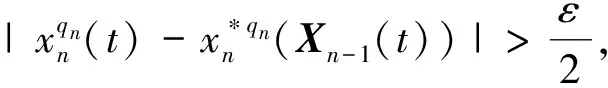
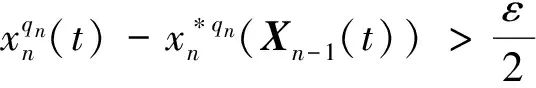
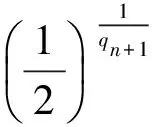
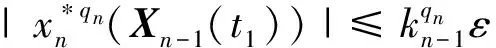

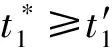
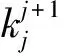


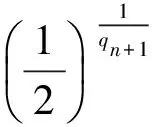

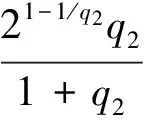

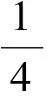
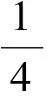
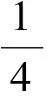
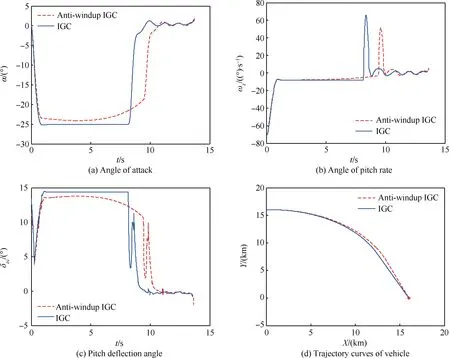
3 仿真校验





4 结 论

