高中数学核心素养在考试评价中的体现

重庆外国语学校 周云龙

高中数学核心素养在考试评价中的体现

重庆外国语学校 周云龙

数学核心素养包括：数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析。这些核心素养既有独立性，又相互交融，形成一个有机整体。 评价是数学教学的指挥棒，如果评价不变，教学目标和教学方法的改变是很难实现的，再好的教育理念也无法得到落实。2017年数学高考全国卷以能力立意，渗透核心素养，核心素养成为高考的热词，因此，从学科核心素养的角度分析高考试题，对以后的教育教学工作有重要的现实意义。 本文以2017年数学高考新课标理科卷2为例，谈一谈数学核心素养在考试评价中的体现。

一、数学核心素养之数学抽象

数学抽象是指舍去事物的一切物理属性，得到数学研究对象的思维过程。 主要包括：从数量到数量关系、图形与图形关系中抽象出数学概念及概念之间的关系，从事物的具体背景中抽象出一般规律和结构，并且用数学符号或者数学术语予以表征。

数学是一门具有高度抽象性的学科，研究对象是由现实世界抽象而来，通过数学抽象，形成数学概念和规则，产生数学命题和模型，催生数学思想与方法，最终形成数学结构与理论体系。 数学抽象是数学的基本思想，是形成理性思维的重要基础，反映了数学的本质特征一般性，贯穿在数学的产生、发展、应用的过程中。

例1 （2017年全国新课标卷2，3题）我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯（ ）

A.1盏 B.3盏 C.5盏 D.9盏

我们从斜抛运动、恩格尔系数与年份等情景中抽象出函数概念，并研究函数的相关性质，高中数学中的函数、不等式、方程、数列、三角函数等都可以在函数的高度统一起来，让学生可以用数学的眼光来观察现实世界。 本题就是以数学文化为背景，从诗歌中抽象出数学问题，使用等比数列解决问题，是数学抽象的典型体现。

二、数学核心素养之逻辑推理

逻辑推理是指从一些事实和命题出发，依据逻辑规则推出一个命题的思维过程。 主要包括两类：一类是从特殊到一般的推理，推理形式主要有归纳、类比；一类是从一般到特殊的推理，推理形式主要有演绎。

数学发展主要依赖的就是逻辑推理，通过逻辑推理得到数学命题和结论。 推理就是从命题判断到命题判断的思维过程；逻辑推理，就是从一些前提或事实出发，根据一定的规则得到或者验证命题的思维过程。 逻辑推理保证了数学的严谨性。

例2 （2017年全国新课标卷2，7题）甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩。老师说：你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩。看后甲对大家说：我还是不知道我的成绩。根据以上信息，则（ ）

A.乙可以知道四人的成绩

B.丁可以知道四人的成绩

C.乙、丁可以知道对方的成绩

D.乙、丁可以知道自己的成绩

解：总共2优2良，甲说了之后——乙、丙成绩1优1良，甲、丁成绩1优1良，根据甲给的信息列出下表：

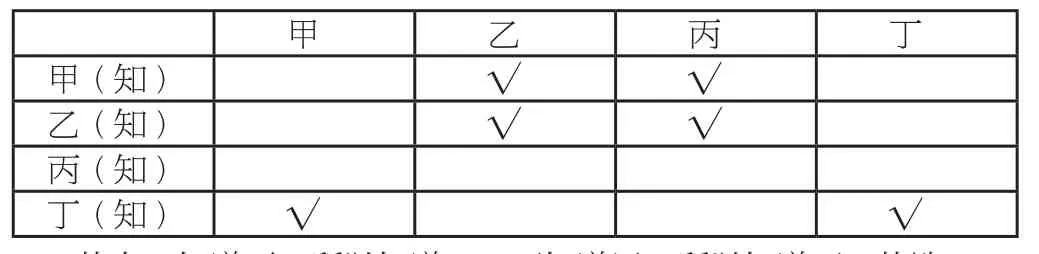
甲乙丙丁甲（知） √ √乙（知） √ √丙（知）丁（知） √ √

故有乙知道丙，所以知道乙，丁知道甲，所以知道丁，故选D。

本题没有公式、没有原理、没有运算、没有成熟的解题套路，需要的只是学生的逻辑推理能力，用数学的思维来思考现实世界。这种通过所学的基础知识获得解决问题的方法，并能用来解决生活实际中遇到的问题，正是逻辑推理这一核心素养的魅力所在。此外，还有题目20，第（1）问以椭圆标准方程为依托，根据线段间向量关系求轨迹方程；第（2）问根据动直线相互垂直证明直线过定点，重点考查思维的灵活性和综合应用知识解决问题的能力。同时还有题目21等，都是经典的逻辑推理考题。

2017年修订后的数学学科考试大纲削枝强干，加强主体内容，强调理性思维的考查。故本卷把考查逻辑推理能力作为命题的首要任务，运用数学知识作为载体，考查学生的缜密思维、严格推理能力。创新题目设计，运用日常生活语言和情境考查逻辑推理能力，在7题、20题、21题中体现明显。

三、数学核心素养之数学建模

数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学知识与方法构建模型解决问题的过程。主要包括：在实际情境中从数学的视角发现问题、提出问题，分析问题、构建模型，求解结论，验证结果并改进模型，最终解决实际问题。

数学模型构建了数学与外部世界的桥梁，在现代社会，几乎所有的学科在科学化的过程中都要使用数学语言，通过建立数学模型刻画研究对象的性质、关系和规律，是数学应用的重要形式，体现了数学的广泛性。

例3 （2017年全国新课标卷2，5题） 设x，y满足约束条件

A.-15 B.-9 C.1 D.9

解：把不等式转化为函数模型，绘制不等式组表示的可行域，如图1所示，结合目标函数可得函数在点处取得最小值：，故选A。

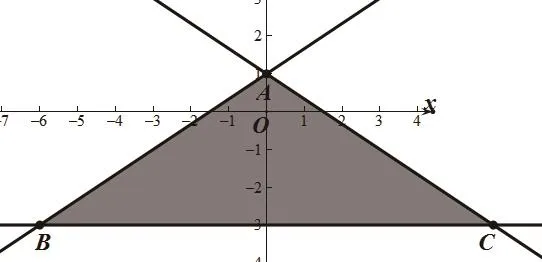
图1

利用数学建模解决实际应用问题，首先要正确理解题意，分析条件和结论，理顺关系；其次建立恰当的函数模型，将文字语言、图形或数据表格转化为数学语言，将实际问题转化为数学问题，再利用数学知识求解，用数学的语言表达现实世界。

四、数学核心素养之数学运算

数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的过程。 主要包括：理解运算对象，掌握运算法则，探究运算方向，选择运算方法，涉及运算程序，求得运算结果等。

数学运算时，数学活动的基本形式是得到数学结果的重要手段，也是属于逻辑推理的一种形式，故数学运算和逻辑推理往往交融在一起，共同考查。

例4 （2017年全国新课标卷2，21题） 已知函数f(x)=ax2-ax-xlnx，（1）求a；（2）证明：存在唯一的极大值点

本题考查导数的运算，利用导数求函数的单调性、最值，解决函数值的范围问题，考查学生的逻辑推理和数学运算能力。数学离不开运算，运算包括对数值的计算，估值和近似计算，对式子的组合与分解，对几何图形形与量的计算等。运算准确、快速，思维严谨和步骤完整是数学运算的基本要求，数学运算是逻辑推理的保证，是高中数学的必考点。

五、数学核心素养之直观想象

直观想象是指借助几何直观和空间想象感知事物的形态和变化，利用图形理解和解决数学问题的过程。 主要包括：借助空间认识事物的位置关系、形态变化与运动规律；利用图形描述、分析数学问题；建立形与数的联系；构建数学问题的直观模型，探索解决问题的思路。

直观想象是探索和形成论证思路、进行逻辑推理、构建抽象结构的思维基础，是发现和提出数学问题、分析和解决数学问题的重要手段。 直观想象和数学抽象关系密切，往往交融在一起考查。

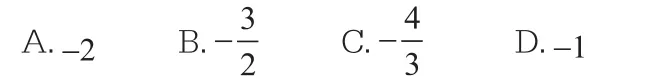
解：以BC边所在直线为x轴，过A垂直于BC的直线为y轴，建立如图2所示的坐标系：

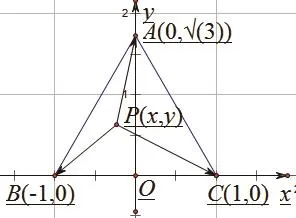
图2

本题利用几何直观赋予向量以坐标，把向量问题转化为函数问题，从而可以快速解出。通过直观想象，提升数形结合的能力，建立良好的数学直觉，理解事物本质和发展规律。此外，还有题目10、题目19等涉及直观想象。

六、数学核心素养之数据分析

数据分析是指针对研究对象获得相关数据，运用统计方法对数据中的有用信息进行分析和推断，从而形成知识的过程。 主要包括：收集数据，整理数据，提取信息，构建模型，对信息进行分析、推断获得结论。

数据分析和数学建模关系密切，是大数据时代数学应用的主要方法，已经深入到现代生活和科学研究的各个方面。

例6 （2017年全国新课标卷2，18题）海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100 个网箱，测量各箱水产品的产量（单位：kg）某频率分布直方图如下：

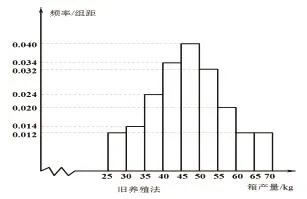
图3-1

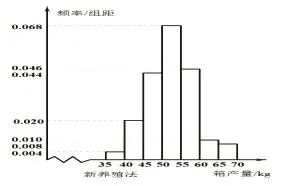
图3-2

（1）设两种养殖方法的网箱产量相互独立，记A表示事件：“旧养殖法的箱产量低于50kg，新养殖法的箱产量不低于50kg”，估计A的概率；

（2）填写下面的列联表，并根据列联表判断是否有99%的把握认为网箱产量与养殖方法有关：

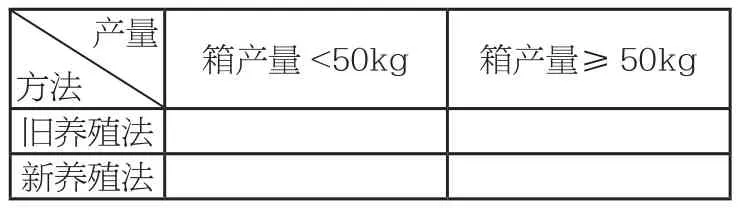
箱产量＜50kg 箱产量≥50kg旧养殖法新养殖法

（3）根据网箱产量的频率分布直方图，求新养殖法网箱产量的中位数的估计值（精确到0.01），

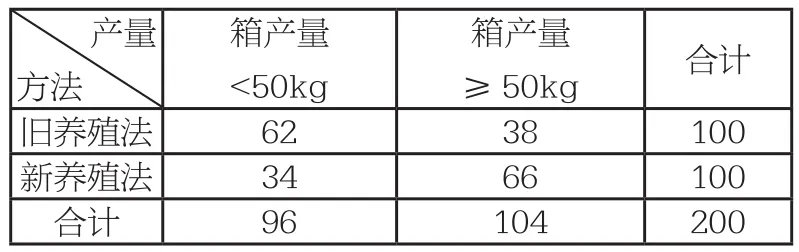
箱产量＜50kg箱产量≥50kg 合计旧养殖法 62 38 100新养殖法 34 66 100合计 96 104 200

（2）

（3）新养殖法中，30～50的频率为0.34，所以中位数估计为

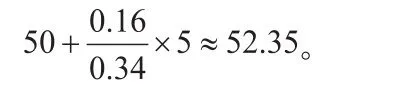
采集数据，分析数据，从复杂数据中提炼出有效信息，提升数据处理能力，增强基于数据分析表达现实问题的意识，养成通过数据思考问题的习惯，积累依托数据探索事物本质、关联和规律的活动经验

2017年数学高考新课标理科2卷遵循课标要求，以知识为载体，以思维能力为核心，全面考查学生的推理论证、运算、空间想象、数据处理以及应用和创新能力。全卷加强对理性思维的考查，突出选拔性，渗透数学文化，体现基础性，加强对应用能力的考查，增强实践性，考查通法通解，凸显创新性。试题坚持能力立意为原则，体现了对“核心素养”的考查，体现了数学的科学价值和理性价值。

核心素养在数学教学中该如何落实呢？把握数学的本质；创设合适的教学情境、提出合适的数学问题；启发学生独立思考、鼓励学生与他人交流；使学生在掌握知识技能的同时，感悟数学本质；积累数学思维和实践的经验、形成和发展数学核心素养。高中数学教育的目标是培养：具备数学抽象和直观想象素养，会用数学的眼光观察世界的人；具备逻辑推理和数学运算素养，会用数学的思维思考现实世界的人；具备数学建模和数据分析素养，会用数学的语言表达现实世界的人。我们任重道远。

[1]史宁中.高中数学核心素养的培养、评价与教学实施[J].中小学教材教学，2017（5）：4-9.

[2]马云鹏.关于数学核心素养的几个问题[J].课程教材教法，2015（9）：36-39.

[3]沈婕，傅剑.数学核心素养视角下的考生水平评价分析及教学建议[J].考试研究，2017（2）：12-22.

[4]史宁中.数学思想概论（第1辑）：数量与数量关系的抽象[M].长春：东北师范大学出版社，2008：1.