课堂适时提问，提升教学效益

江苏省海门市六甲初级中学 陆炜锋

课堂适时提问，提升教学效益

江苏省海门市六甲初级中学 陆炜锋

郑毓信教授提出教师的三项基本功是：善于举例、善于提问、善于比较与优化。而善于提问作为师生交流最密切的一种方式，在数学教学中起到举足轻重的作用，因为课堂上的提问是懂的教师向不懂的学生提问，所以这也是教师稚化思维教学的一种表现形式。我们在课堂上要处理好为什么问、问什么、什么时候问的问题。本文基于这三个方面的思考，结合近年来课堂教学的案例，试图对适时提问（追问）和教学立意做一思考，希望能抛砖引玉。

一、适时提问案例与教学立意解读

1.指向表现形式

案例1：3000用科学记数法表示为______________。你有什么发现？300000如何用科学记数法表示？

追问1：30万用科学记数法表示为__________。你能想出两种表示方法吗？

追问2：三千万用科学记数法表示为__________。

追问3：3亿用科学记数法表示为__________。

追问4：在我国南海某海域探明可燃冰储量约有194亿立方米，如何用科学记数法表示？你能改变题目，使答案只有一种表示形式吗？

教学立意：设计的这四个追问，其实都是考查的同一个知识点，就是含文字的数值如何用科学记数法表示，即改变题目的呈现形式，从文字理解上去分析问题，从而得出两种表示方法，并总结出千、万、亿等数值的科学记数法的规律。让学生了解到如果既有数值又有文字时，要分析两种情况，根据问题解答，从而提高了学生分类讨论的敏感度和解决问题的严谨性。

2.指向自然生成

案例2：已知一次函数y=kx+1的图象经过点（1，0），则k=___________。

追问1：一次函数y=kx+b的图象经过点（-2，3）和（1，0），那么这个一次函数的解析式为___________。

追问2：已知一次函数的图象过点(1，0)与（-2，3），求这个一次函数的解析式。

追问3：根据下表中一次函数的自变量x与函数值y的对应值，可得p的值为( )。

x -2 0 1 y 3 p 0

A.l B. -1 C. 3 D. -3

教学立意：本题是一次函数求解析式的题目，原题很简单，某些学生口算都能完成。随后逐问深入，追问1是将一个点变成了两个点，并让学生很自然地想到因为要求两个未知数k和b，所以需要两个条件；追问2没有解析式，要让学生自然而然地想到先设解析式，从而引出待定系数法；追问3既没有经过的点，也没有要学生求解析式，但学生会自然地把表格形式变为坐标形式，并设解析式，这种“下套”的方式，学生易于自然生成解答。

最后对于追问3的问题，我又设计了一个问题：如果不求解析式，如何得出p的值？这其实是利用了k的另一种求法，用两点的纵坐标的差除以它们的横坐标的差，求解时选择的数字不一样，计算的难易程度也不相同，形成了开放式的教学形式和一题多解的理念。

3.指向开放教学

案例3：如图所示，已知△ABC∽△ADB，且CB＝3，AC＝4，试求BD的长。

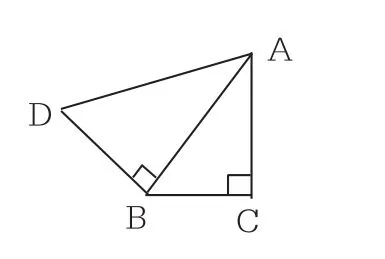
追问1：若把“△ABC∽△ADB”改为“△ABC和△ADB相似”，BD的长是多少？

追问2：求CD的长度。

追问3：你还能改变条件或结论，设计一个新的题目吗？

教学立意：追问1的意图就是知道斜边AD与AB是对应边，但另外两条直角边的对应关系就不明确，故必须分类讨论；追问2的意图则是突然出现求CD的长度，指向“四面八方”，学生无从下手，而实际上还是利用“一线三等角”的模型构造相似三角形，利用勾股定理解题。两个问题方向不一样，一个是改变条件，一个是改变求解，既考查了数学的严谨性，又考查了数学的开放性。追问3设计了学生编题，指向开放的教和放开的学。

4.指向学科德育

案例4：某广告公司欲招聘策划人员一名，对甲、乙、丙三名候选人进行三项素质测试，他们的各项成绩如下表所示：

?

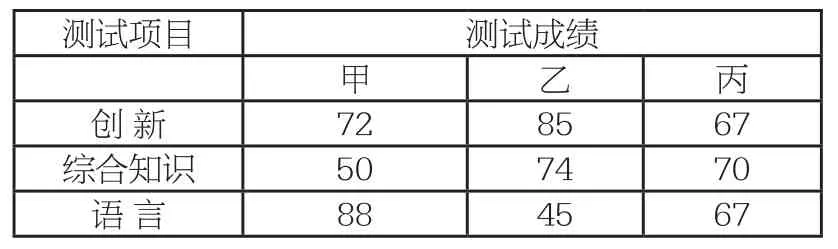
（1）如果根据三项测试的平均成绩确定录用人选，那么谁将被录用？

（2）根据实际需要，若公司将创新、综合知识和语言三项测试得分按分别占50%、30%和20%的比例确定最终的测试成绩，此时谁将被录用？

追问：若录用丙，则该如何调整各项测试成绩的权？

教学立意：其实丙的成绩在前两种计算中是比较差的，但是设置这样的一个问题学生就产生了兴趣，在学生自主解决后，引导学生思考两个方面的内容：一是要让学生建立自信，一个看上去明显差于别人的人，也会有自己的优点，也能突破极限，二是通过改变权重，将一个看上去能力不行的人成功录用，有时候在公平性上是说不过去的，这违背了选择的初衷，要让学生知道其实加权平均数是一把“双刃剑”，要用好“这把剑”，不管是现在还是以后走上社会，都要做一个有底线的人。

二、写在最后

章建跃教授说：保证课堂教学质量和效益的两个关键是“自然的过程”和“恰时恰点的问题”。所以对于课堂中的提问，有课前对学材的再建构，也有课堂上由学生引发的新的追问，如何才能恰时恰点地提出问题而又不显得突兀，这是一个需要教师长期实践和反思的问题。上面的四个案例只是管中窥豹，其实每堂课都有追问，都有对话，而如何深度地进行对话需要我们大家一起行动起来。

【备注：本文系江苏省教育科学十三五初中重点资助课题《初中数学“学材再建构”研究》（课题编号：E-a/2016/06；主持人：施俊进、徐强）主要研究成果之一。】